Похожие презентации:
Трудности расчета турбулентных потоков (неустойчивость процессов)
1. Пример: трудности расчета турбулентных потоков (неустойчивость процессов)
Основы теории турбулентного переносаПример: трудности расчета турбулентных потоков
(неустойчивость процессов)
23.05.2019
1
2.
Основы теории турбулентного переносаЧто такое турбулентность ?
Турбулентный поток является сложным трехмерным нестационарным
течением, характеризующимся хаотичным движением, пульсациями
скорости и интенсивным смешением (большие числа Рейнольдса).
Один из
первых
опытов:
Рейнольдс
(1883)
?Увеличение
вязкости при
переходе к
турбулентному
движению?
23.05.2019
2
3. Характеристики турбулентности (Х.Т.) – турбулентные вихри
Основы теории турбулентного переносаХарактеристики турбулентности (Х.Т.) – турбулентные вихри
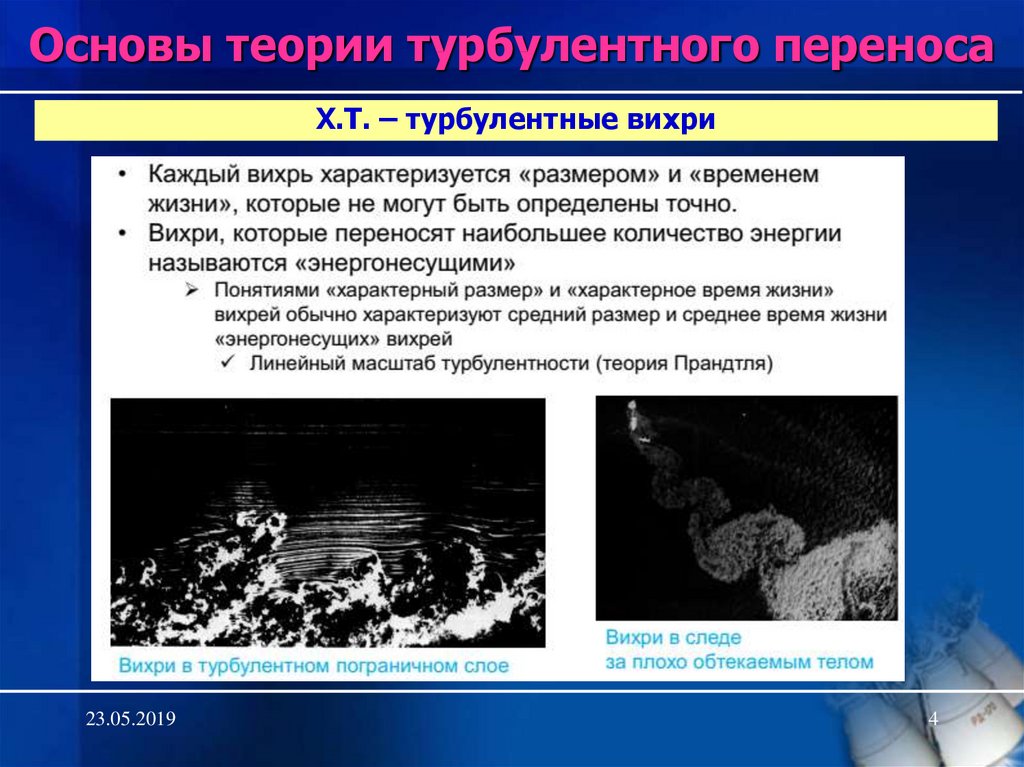
Турбулентность – это совокупность турбулентных вихрей различного
размера
23.05.2019
3
4. Х.Т. – турбулентные вихри
Основы теории турбулентного переносаХ.Т. – турбулентные вихри
23.05.2019
4
5. Х. Т. – линейный масштаб турбулентности
Основы теории турбулентного переносаХ. Т. – линейный масштаб турбулентности
23.05.2019
5
6. Х. Т. – статистическая теория турбулентности
Основы теории турбулентного переносаХ. Т. – статистическая теория турбулентности
23.05.2019
6
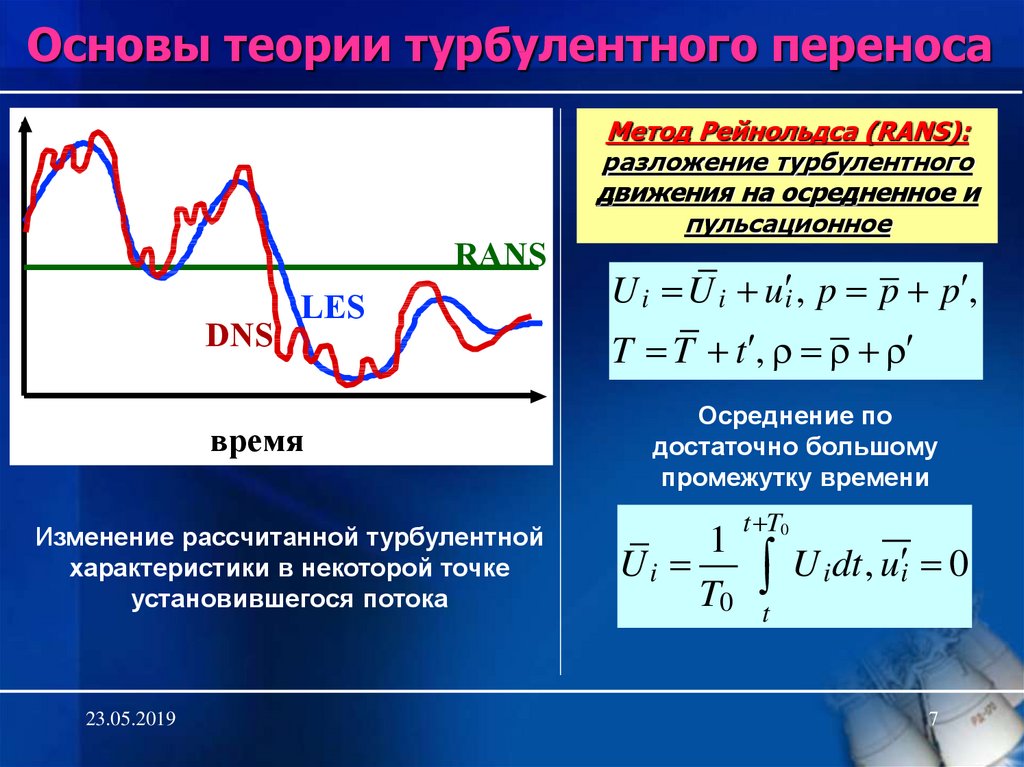
7. Метод Рейнольдса (RANS): разложение турбулентного движения на осредненное и пульсационное
Основы теории турбулентного переносаRANS
DNS
LES
время
Изменение рассчитанной турбулентной
характеристики в некоторой точке
установившегося потока
23.05.2019
Метод Рейнольдса (RANS):
разложение турбулентного
движения на осредненное и
пульсационное
U i U i u i , p p p ,
T T t ,
Осреднение по
достаточно большому
промежутку времени
1
Ui
T0
t T0
U i dt , u i 0
t
7
8. Условия РЕЙНОЛЬДСА
Основы теории турбулентного переносаУсловия РЕЙНОЛЬДСА
Правила осреднения искомых функций
f f
f f , f g f g, f g f g,
, f dq f dq
q q
1
Ui
T0
1
u i
T0
2
1
u i
T0
t T0
t T0
t
t T0
n
23.05.2019
t
Осредненное значение скорости
(математическое ожидание)
U i dt
t
1
(U i U i ) dt
T0
2
1
(U i U i ) dt
T0
n
t T0
t
t T0
u i dt
Дисперсия пульсаций
скорости (второй
статистический момент)
u i n dt
n-ый центральный
статистический момент
2
t
8
9. Х. Т. – осреднение по времени (по Рейнольдсу)
Основы теории турбулентного переносаХ. Т. – осреднение по времени (по Рейнольдсу)
1
Ui
T0
23.05.2019
t T0
U i dt , u i 0
t
9
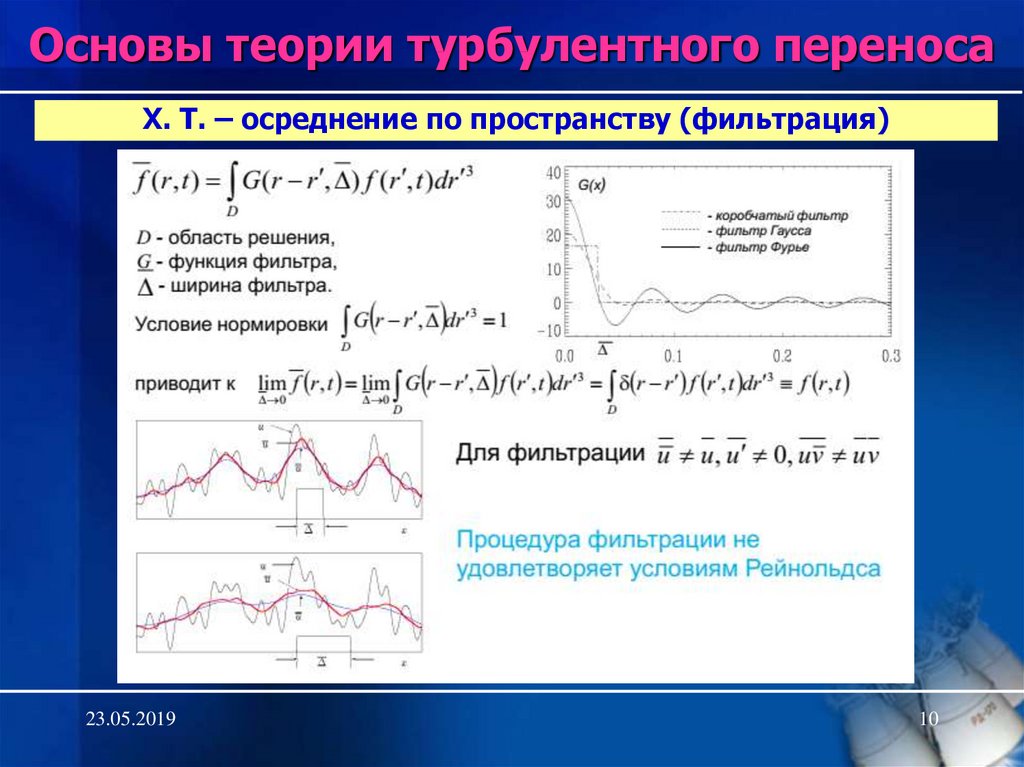
10. Х. Т. – осреднение по пространству (фильтрация)
Основы теории турбулентного переносаХ. Т. – осреднение по пространству (фильтрация)
23.05.2019
10
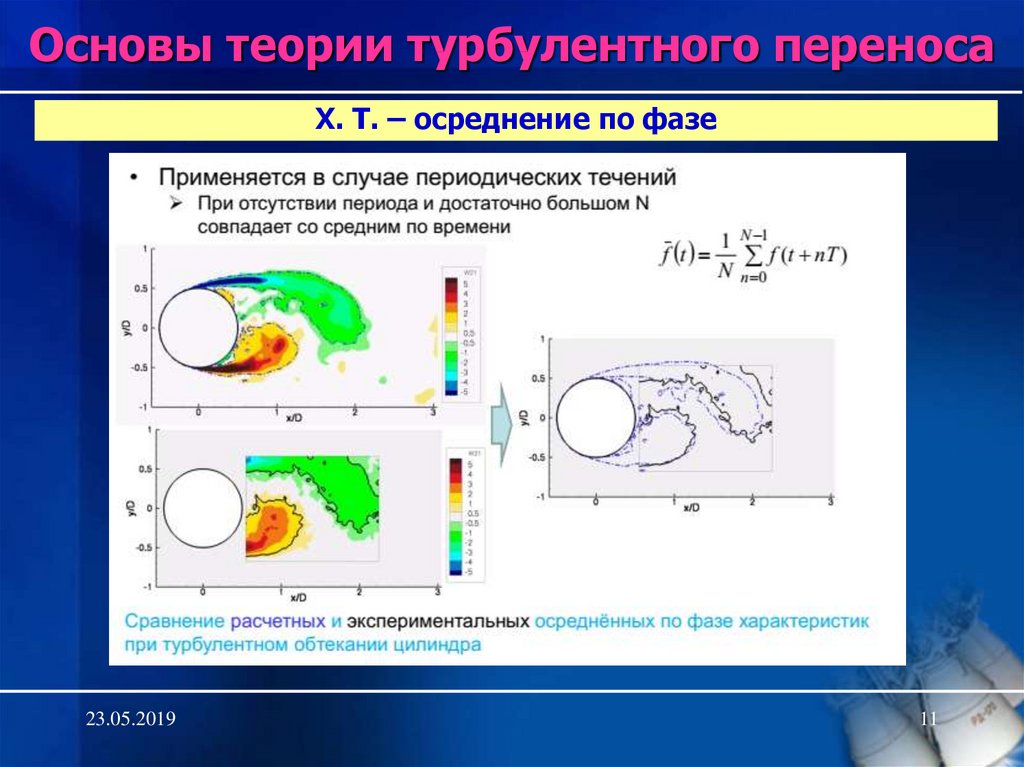
11. Х. Т. – осреднение по фазе
Основы теории турбулентного переносаХ. Т. – осреднение по фазе
23.05.2019
11
12. Х. Т. – корреляции и автокорреляционные коэффициенты
Основы теории турбулентного переносаХ. Т. – корреляции и автокорреляционные коэффициенты
23.05.2019
12
13. Х. Т. – интегральные масштабы турбулентности
Основы теории турбулентного переносаХ. Т. – интегральные масштабы турбулентности
23.05.2019
13
14. Х. Т. – кинетическая энергия турбулентности
Основы теории турбулентного переносаХ. Т. – кинетическая энергия турбулентности
23.05.2019
14
15. Х. Т. – одномерный энергетический спектр
Основы теории турбулентного переносаХ. Т. – одномерный энергетический спектр
23.05.2019
15
16. Х. Т. – пространственный энергетический спектр
Основы теории турбулентного переносаХ. Т. – пространственный энергетический спектр
23.05.2019
16
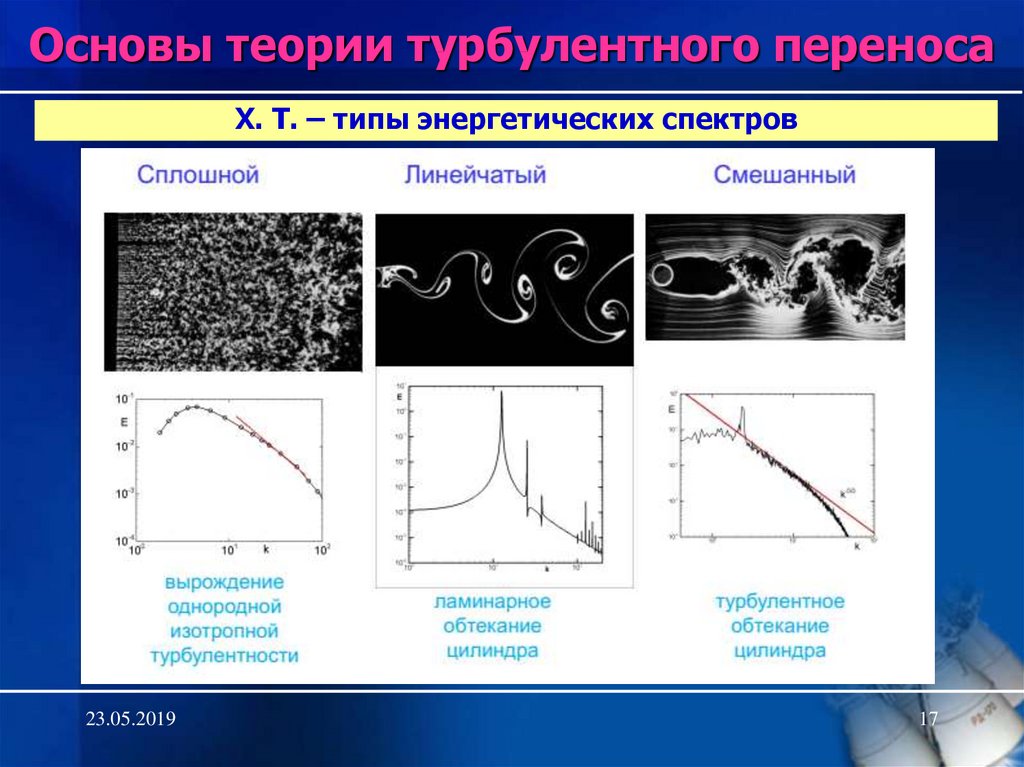
17. Х. Т. – типы энергетических спектров
Основы теории турбулентного переносаХ. Т. – типы энергетических спектров
23.05.2019
17
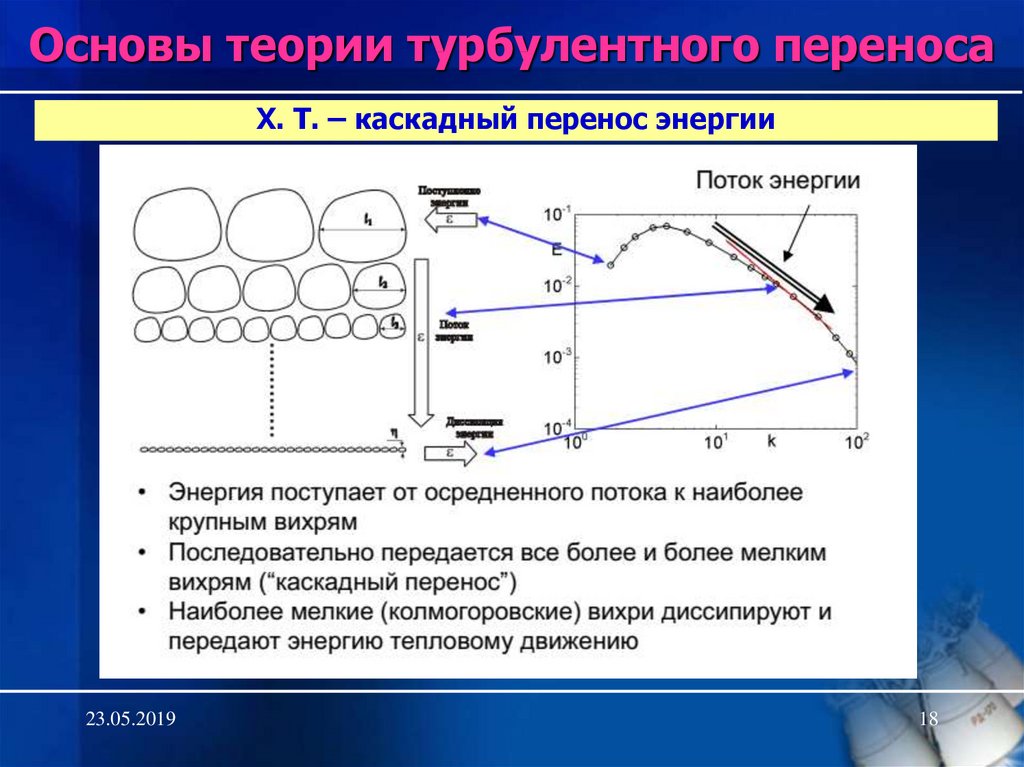
18. Х. Т. – каскадный перенос энергии
Основы теории турбулентного переносаХ. Т. – каскадный перенос энергии
23.05.2019
18
19. Х. Т. – области энергетического спектра
Основы теории турбулентного переносаХ. Т. – области энергетического спектра
23.05.2019
19
20. Х. Т. – двумерные вихри
Основы теории турбулентного переносаХ. Т. – двумерные вихри
23.05.2019
20
21. Промежуточные выводы
Основы теории турбулентного переносаПромежуточные выводы
23.05.2019
21
22.
Основы теории турбулентного переносаУравнения Навье-Стокса – универсальные для турбулентных и
ламинарных потоков
Уравнение неразрывности
Уравнения движения
U i
0
t
xi
U i U iU j
p
t
x j
xi x j
U i U j
xi
x j
2
ij divU Fi
3
Прямое численное моделирование турбулентности на основе уравнений
Навье-Стокса возможно
Но отношение между максимальным и минимальными масштабами
явлений в турбулентном потоке
Колмогоровский масштаб lK минимальный масштаб вихрей
Пример для вычислит елей: Количество узлов
вычислительной сетки для полного
разрешения зависит от числа Рейнольдса
(обычно Re>104)
23.05.2019
22
23.
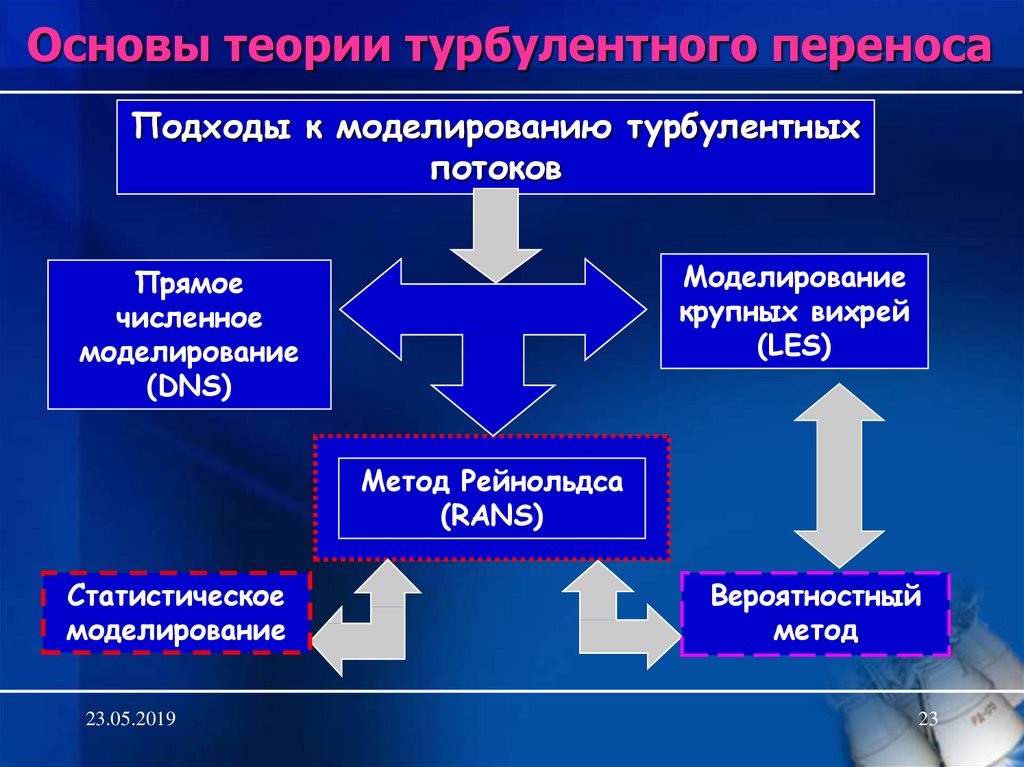
Основы теории турбулентного переносаПодходы к моделированию турбулентных
потоков
Моделирование
крупных вихрей
(LES)
Прямое
численное
моделирование
(DNS)
Метод Рейнольдса
(RANS)
Статистическое
моделирование
23.05.2019
Вероятностный
метод
23
24. МЕТОД РЕЙНОЛЬДСА (RANS)
Основы теории турбулентного переносаМЕТОД РЕЙНОЛЬДСА (RANS)
Анализ турбулентного движения проводится на основе уравнений
Навье-Стокса: посредством подстановки действительных значений
скорости, давления, плотности и проведения осреднения по правилам
получаются уравнения осредненного движения (уравнения Рейнольдса)
Пример: стационарное движение несжимаемой вязкой жидкости
U x U y U z
0
x
y
z
U x
U x
U x 1 xx xy xz
Ux
U y
Uz
x
y
z
x
y
z
U y
U y
U y 1 yx yy yz
Ux
U y
Uz
x
y
z
x
y
z
Ux
23.05.2019
U z
U z
U z 1 zx zy zz
U y
Uz
x
y
z
x
y
z
24
25. МЕТОД РЕЙНОЛЬДСА (RANS)
Основы теории турбулентного переносаМЕТОД РЕЙНОЛЬДСА (RANS)
ТЕНЗОР НАПРЯЖЕНИЙ
U i U j
ij p
xi
x j
u iu j
Новые слагаемые – дополнительные напряжения поверхностных сил,
возникающих из-за наличия турбулентности (турбулентные напряжения,
составляющие тензор). Они причина дополнительной вязкости в потоке
и являются неизвестными параметрами!!!!.
Для замкнутости уравнений Рейнольдса необходимо ввести
дополнительные шесть уравнений, связывающих компоненты тензора
напряжений, но мы СНОВА получим систему незамкнутых уравнений
содержащих величины типа:
u iu j u k ... u iu j u k p ...
23.05.2019
и т.д.
!!!ПРОБЛЕМА ТУРБУЛЕНТНОСТИ!!!
25
26. Влияние турбулентности на пристеночные течения
Основы теории турбулентного переносаВлияние турбулентности на пристеночные течения
1. Рассмотрим установившееся ламинарное течение вдоль
безграничной пластины (скорость зависит только от координаты y,
давление можно считать постоянным)
Уравнения Навье-Стокса вырождаются в
U x
U x
0
y y
y
const wall
y 0
wall
Ux
y C1
Следствие: Для ламинарного потока вдоль безграничной пластины
имеет место линейное распределение скорости (С1=0 т.к. при y=0 Ux=0)
23.05.2019
26
27. Влияние турбулентности на пристеночные течения
Основы теории турбулентного переносаВлияние турбулентности на пристеночные течения
2. Рассмотрим установившееся турбулентное течение вдоль
безграничной пластины (скорость зависит только от координаты y,
давление можно считать постоянным)
Уравнения Рейнольдса
вырождаются в
U x
( u xu y ) 0
y y
Условие на стенке: при y = 0 пульсации скорости
нулевые, поэтому и напряжения нулевые
C 2 wall
U x
y
y 0
U x
xy wall
y
U x
xy C2
y
Следствие: 1 слагаемое: вязкое трение имеет значительную величину вблизи
стенки и убывает с увеличением расстояния
2 слагаемое: турбулентное трение мало у стенки, но возрастает при удалении от
23.05.2019
27
пластины
28. Влияние турбулентности на пристеночные течения
Основы теории турбулентного переносаВлияние турбулентности на пристеночные течения
Область вблизи стенки, в которой вязкое трение преобладает, называется
ламинарным подслоем и для него справедлив закон распределения скоростей
аналогичный ламинарному движению
U x
xy wall
y
Рассмотрим область, где вязкое
трение мало
xy wall
Последняя формула непрактична, т.к. ничего не известно о связи пульсаций скорости с осредненным движением
По аналогии между вязким трением и турбулентным и по анализу размерностей
b
2
dU x
2 a dU x
c
2 dU x
2
xy f
xy
y xy
y wall
dy
dy
dy
Ux
1 wall
ln y C3
Ux A
Логарифмический закон скоростей при турбулентном движении у
стенки (формула Прандтля)
wall y wall
ln
B
23.05.2019
Закон Кармана с учетом ламинарного подслоя (для трубы
А=5.75, В=5.5)
28
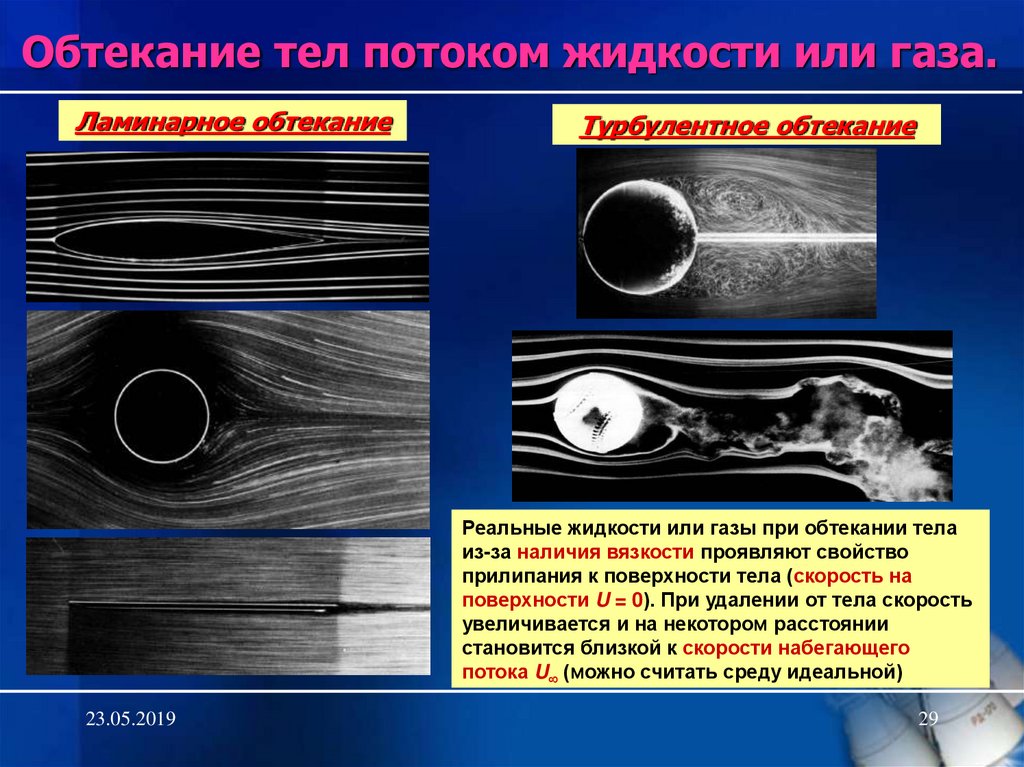
29. Ламинарное обтекание
Обтекание тел потоком жидкости или газа.Ламинарное обтекание
Турбулентное обтекание
Реальные жидкости или газы при обтекании тела
из-за наличия вязкости проявляют свойство
прилипания к поверхности тела (скорость на
поверхности U = 0). При удалении от тела скорость
увеличивается и на некотором расстоянии
становится близкой к скорости набегающего
потока U (можно считать среду идеальной)
23.05.2019
29
30. МЕТОД РЕЙНОЛЬДСА (RANS)
Основы теории турбулентного переносаМЕТОД РЕЙНОЛЬДСА (RANS)
ТЕНЗОР НАПРЯЖЕНИЙ
U i U j
ij p
xi
x j
u iu j
Новые слагаемые – дополнительные напряжения поверхностных сил,
возникающих из-за наличия турбулентности (турбулентные напряжения,
составляющие тензор). Они причина дополнительной вязкости в потоке
и являются неизвестными параметрами!!!!.
Для замкнутости уравнений Рейнольдса необходимо ввести
дополнительные шесть уравнений, связывающих компоненты тензора
напряжений, но мы СНОВА получим систему незамкнутых уравнений
содержащих величины типа:
u iu j u k ... u iu j u k p ...
23.05.2019
и т.д.
!!!ПРОБЛЕМА ТУРБУЛЕНТНОСТИ!!!
30
31. МЕТОД РЕЙНОЛЬДСА (RANS)
Основы теории турбулентного переносаМЕТОД РЕЙНОЛЬДСА (RANS)
ЗАМЫКАНИЕ ТЕНЗОРА НАПРЯЖЕНИЙ: по аналогии с законом вязкого
трения вводится понятие турбулентной вязкости t и записывается
связь турбулентных напряжений с осредненными параметрами потока
U i U j
ij u iu j t
xi
x j
2
ij k
3
t C k 2 /
формула Колмогорова-Прандтля для турбулентной
вязкости
С - константа модели (С 0.09 по результатам опытов в струях,
для течений около стенки)
k – кинетическая энергия турбулентности,
- диссипация кинетической энергии
23.05.2019
1
k u iu i
2
u i u j
2 x j xi
2
31
32.
Основы теории турбулентного переносаПроблема нахождения турбулентной вязкости t к проблеме
определения кинетической энергии и ее диссипации
Перечень основных моделей:
Алгебраические модели (модель пути смешения Прандтля
для одномерного течения)
t l mix
dU
dy
Модели с 1 уравнением (модель Колмогорова для кинетической энергии, модель
Спаларта-Альмареса для эффективной вязкости)
k U j k
U i
k 3/ 2
t k
ij
C D
t
x j
x j
l
x j
Prk x j
Модели с двумя уравнениями (к- модель, к- модель и т.д.)
k U j k
U i
ij
t
x j
x j
x j
t
Prk
U j
U i
2
C 1 ij
C 2
t
x j
k
x j
k x j
23.05.2019
k
x
j
Модели для
Рейнольдсовых
напряжений
t
x
Pr
j
32
33.
Основы теории турбулентного переноса• Разрешение потока:
Для 1 cм3 модельной области:
23.05.2019
Memory
Speed
Year
70
50
Gbytes
50
Gflops
1993
300
50
Tbytes
50
Tflops
2002
1500
50
Pbytes
50
Pflops
2015
33
34.
Литература1. Лойцянский Л. Г. Механика жидкости и газа. М.: Наука, 1970.
904 c.
2. Монин А. С., Яглом А. М. Статистическая гидромеханика. М.:
Наука, 1967.
3. Повх И. Л. Техническая гидромеханика. Л.: Машиностроение,
1969. 524 с.
4. Ландау Л. Д., Лившиц Е. М. Гидродинамика. М.: Наука, 1988.
736 с.
5. Кутателадзе С.С. Анализ подобия и физические модели.
Новосибирск: Наука, 1986.
6. Шлихтинг Г. Теория пограничного слоя. М.: Наука, 1974.
23.05.2019
34


























 Физика
Физика








