Значения тригонометрических функций

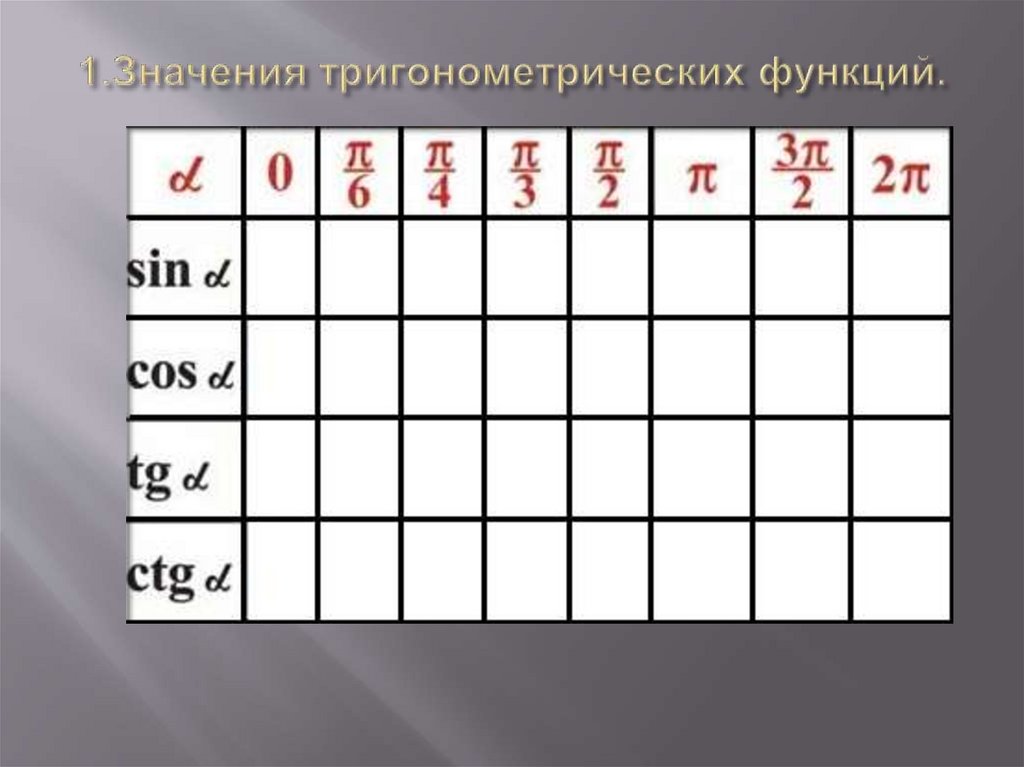
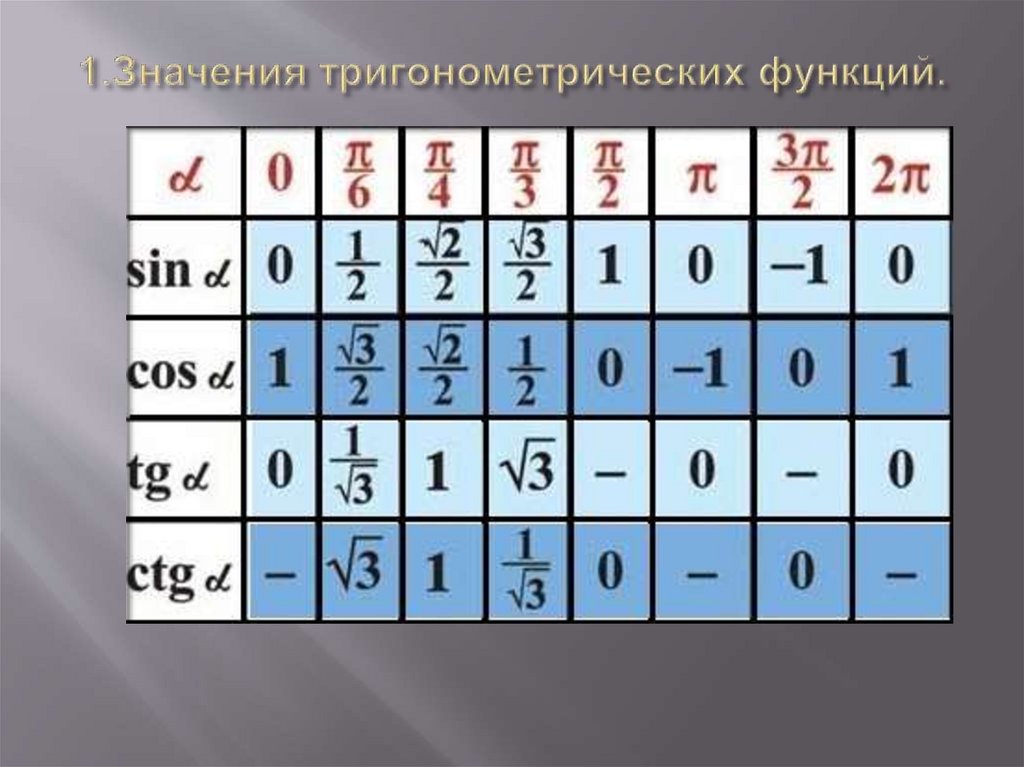
1. 1.Значения тригонометрических функций.

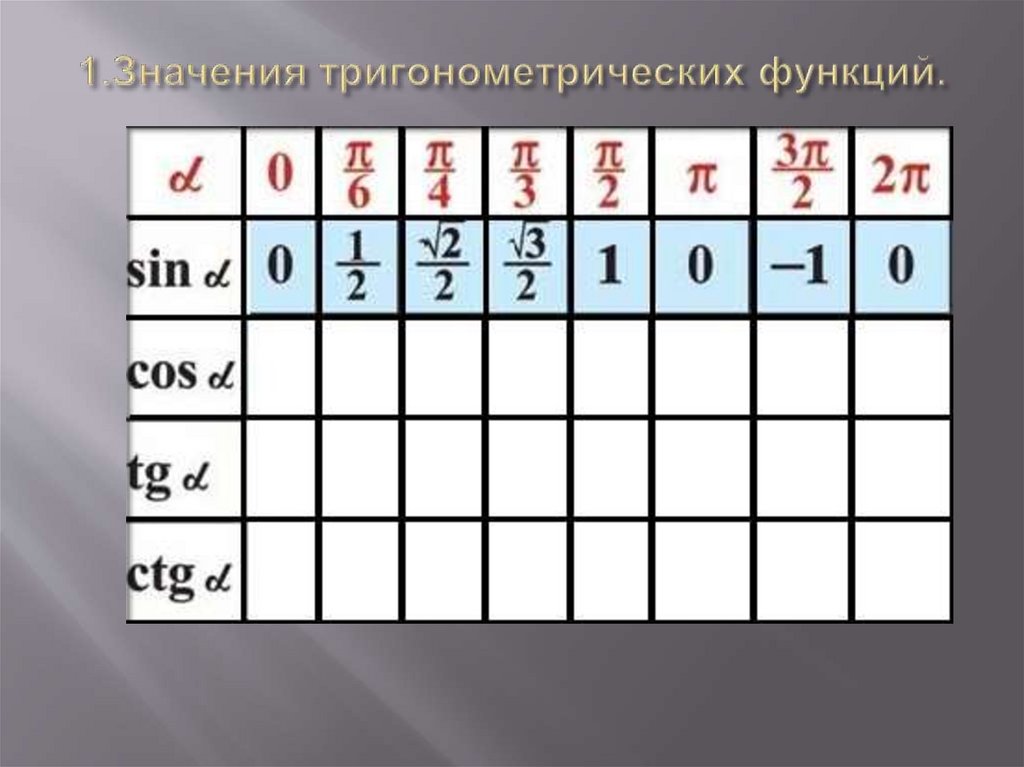
2. 1.Значения тригонометрических функций.

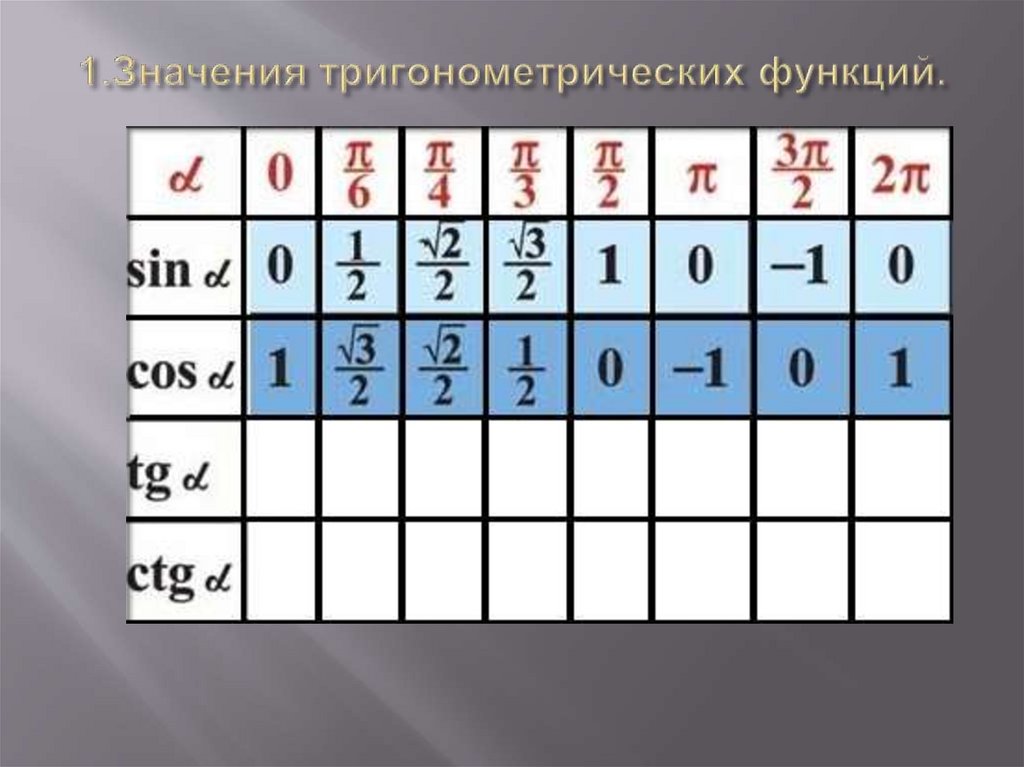
3. 1.Значения тригонометрических функций.

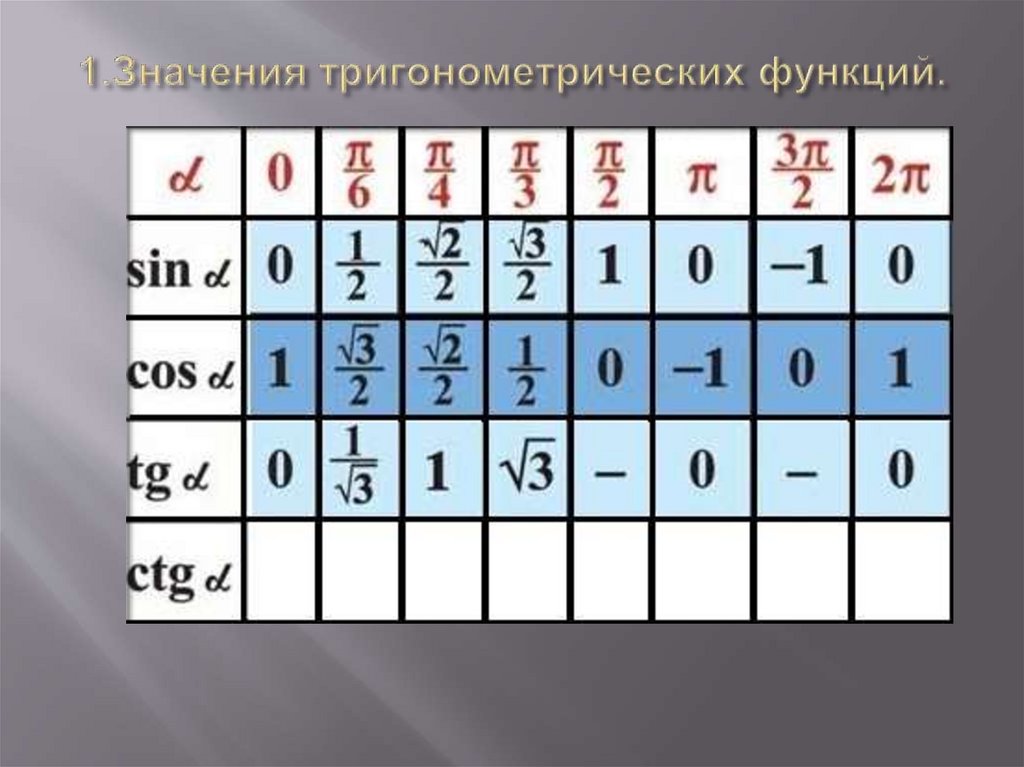
4. 1.Значения тригонометрических функций.

5. 1.Значения тригонометрических функций.

6. 2. Простейшие тригонометрические уравнения:

Решение тригонометрических
уравнений.
1.
2.
3.
4.
sin x = a,
cos x = a,
tg x = a,
ctg x = a,

7. 2. Простейшие тригонометрические уравнения:

Решение тригонометрических
уравнений.
1.
2.
3.
4.
sin x = a,
cos x = a,
tg x = a,
ctg x = a,
x=(-1)ⁿ ∙ arc sin a + n,
nєΖ
│a│≤ 1.

8. 2. Простейшие тригонометрические уравнения:

Решение тригонометрических
уравнений.
1.
2.
3.
4.
sin x = a,
cos x = a,
tg x = a,
ctg x = a,
x=(-1)ⁿ ∙ arc sin a + n,
x=± arc cos a + 2 n,
nєΖ
nєΖ
│a│≤ 1.
│a│≤ 1.

9. 2. Простейшие тригонометрические уравнения:

Решение тригонометрических
уравнений.
1.
2.
3.
4.
sin x = a,
cos x = a,
tg x = a,
ctg x = a,
x=(-1)ⁿ ∙ arc sin a + n,
x=± arc cos a + 2 n,
x= acr tg a + n,
nєΖ
nєΖ
nєΖ
│a│≤ 1.
│a│≤ 1.
a єR .

10. 2. Простейшие тригонометрические уравнения:

Решение тригонометрических
уравнений.
1.
2.
3.
4.
sin x = a,
cos x = a,
tg x = a,
ctg x = a,
x=(-1)ⁿ ∙ arc sin a + n,
x=± arc cos a + 2 n,
x= acr tg a + n,
x= acr ctg a + n,
nєΖ
nєΖ
nєΖ
nєΖ
│a│≤ 1.
│a│≤ 1.
a єR .
a єR .

11. 3. Частные случаи ( а=0, а=1, а=-1)

Sin x = 0,
Sin x = 1,
Sin x = -1,
Cos x = 0,
Cos x = 1,
Cos x =-1,
Tg x = 0,
Ctg x = 0,

12. 3. Частные случаи ( а=0, а=1, а=-1)

Sin x = 0, x = n, nєΖ
Sin x = 1, x = ⁄ 2 + 2 n, nєΖ
Sin x = -1, x = - ⁄ 2 + 2 n, nєΖ
Tg x = 0,
Ctg x = 0,
Cos x = 0,
Cos x = 1,
Cos x =-1,

13. 3. Частные случаи ( а=0, а=1, а=-1)

Sin x = 0, x = n, nєΖ
Sin x = 1, x = ⁄ 2 + 2 n, nєΖ
Sin x = -1, x = - ⁄ 2 + 2 n, nєΖ
Tg x = 0,
Ctg x = 0,
Cos x = 0, x = ⁄ 2 + n, nєΖ
Cos x = 1 , x = 2 n, nєΖ
Cos x =-1, x = + 2 n, nєΖ

14. 3. Частные случаи ( а=0, а=1, а=-1)

Sin x = 0, x = n, nєΖ
Sin x = 1, x = ⁄ 2 + 2 n, nєΖ
Sin x = -1, x = - ⁄ 2 + 2 n, nєΖ
Cos x = 0, x = ⁄ 2 + n, nєΖ
Cos x = 1 , x = 2 n, nєΖ
Cos x =-1, x = + 2 n, nєΖ
Tg x = 0, x = n, nєΖ
Ctg x = 0, x = ⁄ 2 + n, nєΖ

15.

4.Основные тригонометрические тождества
sin² α + cos² α =

16.

4.Основные тригонометрические тождества
sin² α + cos² α = 1
tg α ∙ ctg α =

17.

4.Основные тригонометрические тождества
sin² α + cos² α = 1
tg α ∙ ctg α = 1
tg α =

18.

4.Основные тригонометрические тождества
sin² α + cos² α = 1
tg α ∙ ctg α = 1
tg α = sin α / cos α
ctg α =

19.

4.Основные тригонометрические тождества
sin² α + cos² α = 1
tg α ∙ ctg α = 1
1 + tg² α =
tg α = sin α / cos α
ctg α = cos α / sin α

20.

4.Основные тригонометрические тождества
sin² α + cos² α = 1
tg α ∙ ctg α = 1
1 + tg² α = 1/ cos² α
1 + ctg² α =
tg α = sin α / cos α
ctg α = cos α / sin α

21.

4.Основные тригонометрические тождества
sin² α + cos² α = 1
tg α ∙ ctg α = 1
1 + tg² α = 1/ cos² α
1 + ctg² α = 1/ sin² α
tg α = sin α / cos α
ctg α = cos α / sin α

22. 5. Формулы суммы и разности аргументов.

sin (x ± y) =

23. 5. Формулы суммы и разности аргументов.

sin (x ± y) = sin x ∙ cos y ± cos x ∙ sin y
cos (x ± y) =

24. 5. Формулы суммы и разности аргументов.

sin (x ± y) = sin x ∙ cos y ± cos x ∙ sin y
cos (x ± y) = cos x ∙ cos y ∓ sin x ∙ sin y
tg (x ± y) =

25. 5. Формулы суммы и разности аргументов.

sin (x ± y) = sin x ∙ cos y ± cos x ∙ sin y
cos (x ± y) = cos x ∙ cos y ∓ sin x ∙ sin y
tg (x ± y) = ( tg x ± tg y ) / ( 1 ∓ tg x ∙ tg y )

26. 6. Формулы двойного аргумента(тройного).

sin 2 α =
cos 2 α =
tg 2 α =
sin 3 α =
cos 3 α =
tg 3 α =

27. 6. Формулы двойного аргумента(тройного).

sin 2 α = 2sin α ∙ cos α
cos 2 α =
tg 2 α =
sin 3 α =
cos 3 α =
tg 3 α =

28. 6. Формулы двойного аргумента(тройного).

sin 2 α = 2sin α ∙ cos α
cos 2 α = cos² α - sin² α
tg 2 α =
sin 3 α =
cos 3 α =
tg 3 α =

29. 6. Формулы двойного аргумента(тройного).

sin 2 α = 2sin α ∙ cos α
cos 2 α = cos² α - sin² α
tg 2 α = 2tg α / (1-tg² α)
sin 3 α =
cos 3 α =
tg 3 α =

30. 6. Формулы двойного аргумента(тройного).

sin 2 α = 2sin α ∙ cos α
cos 2 α = cos² α - sin² α
tg 2 α = 2tg α / (1-tg² α)
sin 3 α = 3sin α - 4sin³ α
cos 3 α =
tg 3 α =

31. 6. Формулы двойного аргумента(тройного).

sin 2 α = 2sin α ∙ cos α
cos 2 α = cos² α - sin² α
tg 2 α = 2tg α / (1-tg² α)
sin 3 α = 3sin α - 4sin³ α
cos 3 α = 4cos³ α - 3cos α
tg 3 α =

32. 6. Формулы двойного аргумента(тройного).

sin 2 α = 2sin α ∙ cos α
cos 2 α = cos² α - sin² α
tg 2 α = 2tg α / (1-tg² α)
sin 3 α = 3sin α - 4sin³ α
cos 3 α = 4cos³ α - 3cos α
tg 3 α = (3tg x – tg³ α) / (1-3tg² α)

33. 7. Формулы половинного аргумента или формулы понижения степени.

sin² α /2 =
cos² α /2 =
tg α /2=

34. 7. Формулы половинного аргумента или формулы понижения степени.

sin² α /2 = (1-cos α) /2
cos² α /2 =
tg α /2=

35. 7. Формулы половинного аргумента или формулы понижения степени.

sin² α /2 = (1-cos α) /2
cos² α /2 = (1+cos) /2
tg α /2=

36. 7. Формулы половинного аргумента или формулы понижения степени.

sin² α /2 = (1-cos α) /2
cos² α /2 = (1+cos) /2
tg α /2= sin α / (1+cos α) = (1-cos α) /sin α

37. 8.Формулы для преобразования суммы и разности тригонометрических функций в произведение.

sin x ± sin y =
cos x + cos y =
cos x – cos y =
tg x ± tg y =

38. 8.Формулы для преобразования суммы и разности тригонометрических функций в произведение.

sin x ± sin y = 2 sin (x ± y)/2 ∙ cos (x ∓ y)/2
cos x + cos y =
cos x – cos y =
tg x ± tg y =

39. 8.Формулы для преобразования суммы и разности тригонометрических функций в произведение.

sin x ± sin y = 2 sin (x ± y)/2 ∙ cos (x∓y)/2
cos x + cos y = 2 cos (x+y)/2 ∙ cos (x-y)/2
cos x – cos y =
tg x ± tg y =

40. 8.Формулы для преобразования суммы и разности тригонометрических функций в произведение.

sin x ± sin y = 2sin (x ± y)/2 ∙ cos (x∓y)/2
cos x + cos y = 2cos (x+y)/2 ∙ cos (x-y)/2
cos x – cos y = -2sin (x+y)/2 ∙sin (x-y)/2
tg x ± tg y =

41. 8.Формулы для преобразования суммы и разности тригонометрических функций в произведение.

sin x ± sin y = 2sin (x ± y)/2 ∙ cos (x∓y)/2
cos x + cos y = 2cos (x+y)/2 ∙ cos (x-y)/2
cos x – cos y = -2sin (x+y)/2 ∙sin (x-y)/2
tg x ± tg y = (sin ∙(x ±y))/(cos x∙ cos y)

42. 9.Формулы приведения:

1)
/2 и 3 /2 │ =>
и 2
│ =>
2) Знаки по четвертям:
sin α
cos α
tg α, ctg α

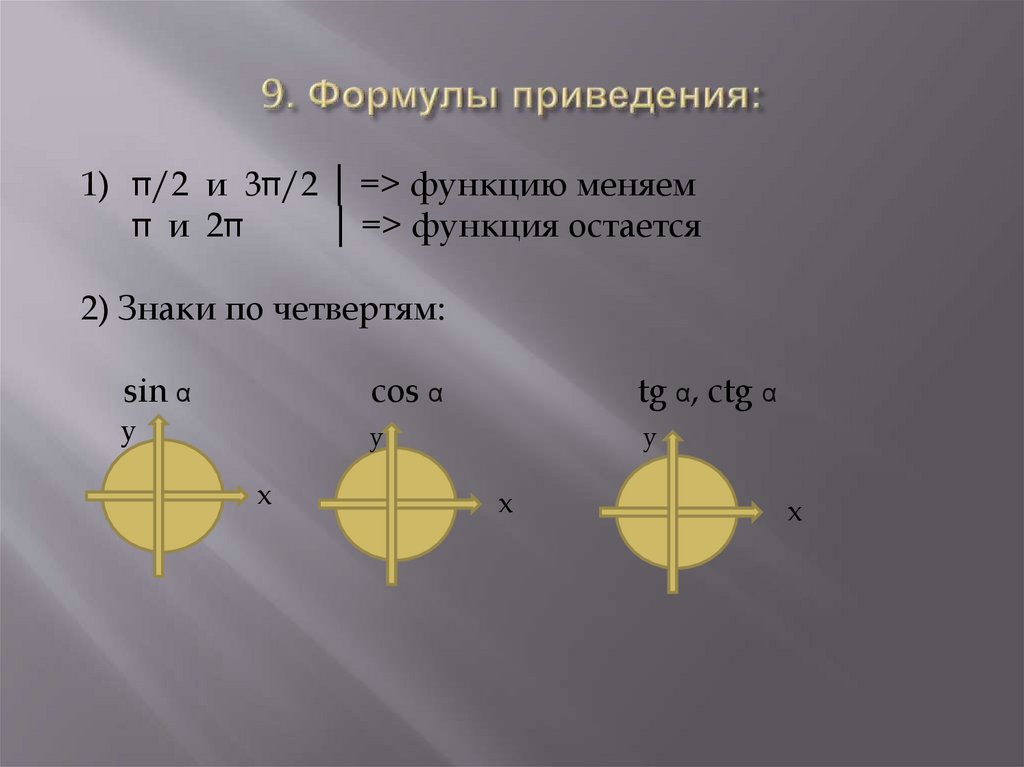
43. 9. Формулы приведения:

1)
/2 и 3 /2 │ => функцию меняем
и 2
│ =>
2) Знаки по четвертям:
sin α
cos α
tg α, ctg α

44. 9. Формулы приведения:

1)
/2 и 3 /2 │ => функцию меняем
и 2
│ => функция остается
2) Знаки по четвертям:
sin α
cos α
tg α, ctg α

45. 9. Формулы приведения:

1)
/2 и 3 /2 │ => функцию меняем
и 2
│ => функция остается
2) Знаки по четвертям:
sin α
cos α
tg α, ctg α
y
y
y
x
x
x

46. 9. Формулы приведения:

1)
/2 и 3 /2 │ => функцию меняем
и 2
│ => функция остается
2) Знаки по четвертям:
sin α
cos α
y
y
+
-
-
+
-
x
tg α, ctg α
y
x
x

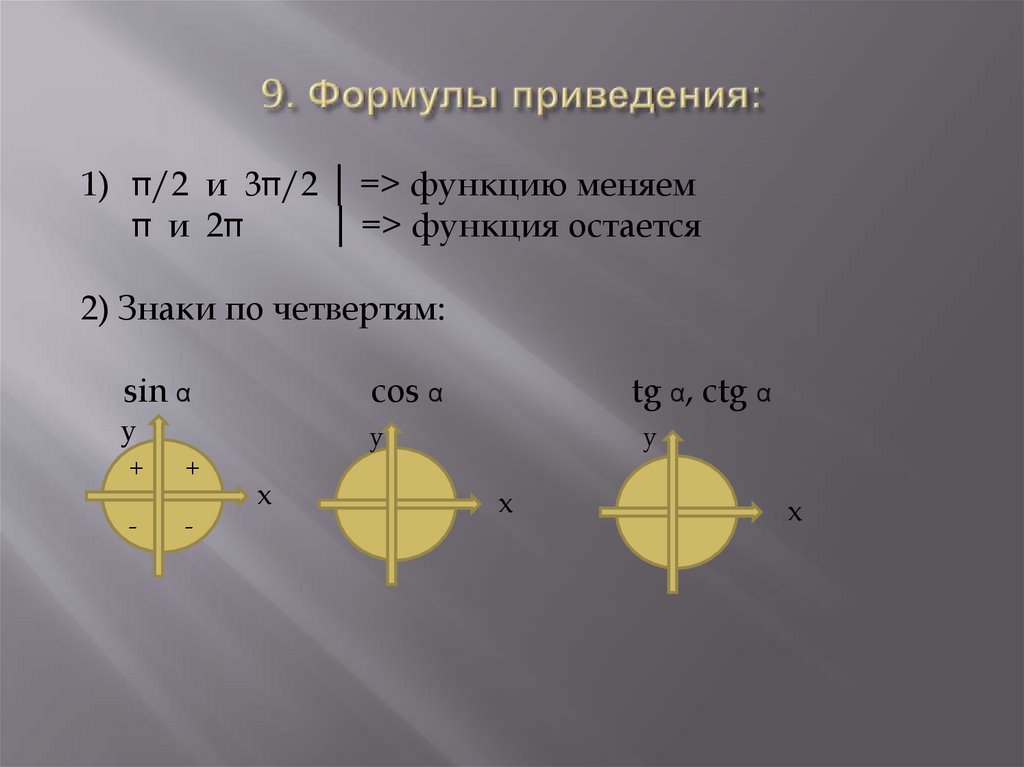
47. 9. Формулы приведения:

1)
/2 и 3 /2 │ => функцию меняем
и 2
│ => функция остается
2) Знаки по четвертям:
sin α
cos α
y
+
-
tg α, ctg α
y
-
+
-
x
y
-
+
-
+
x
x

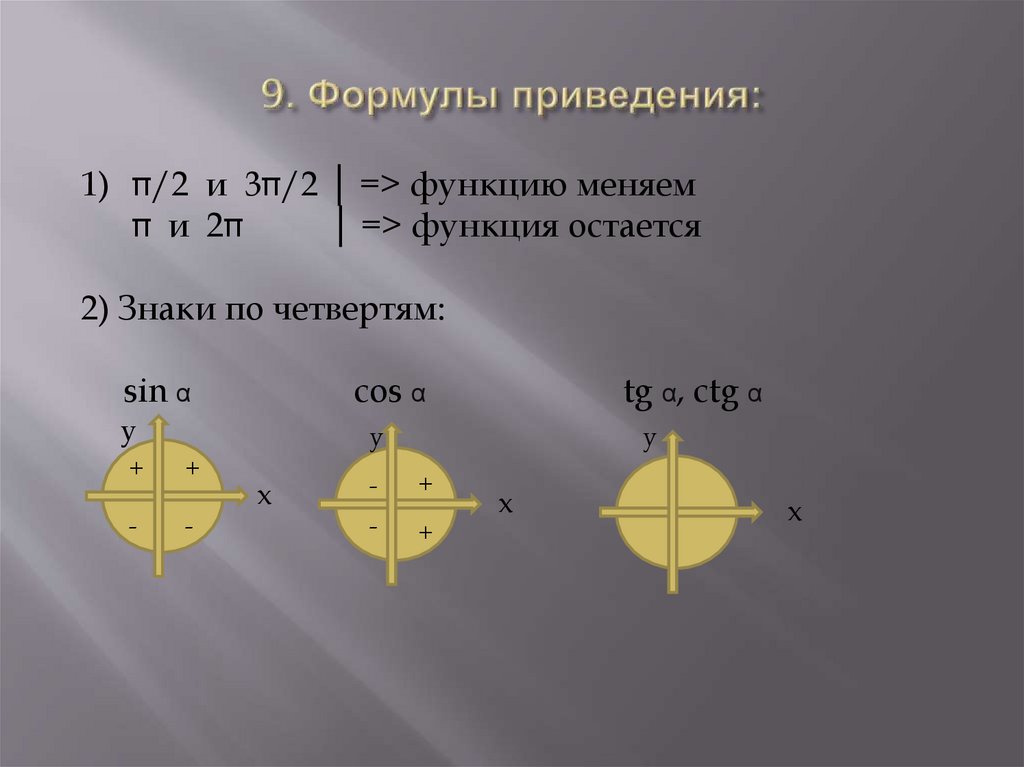
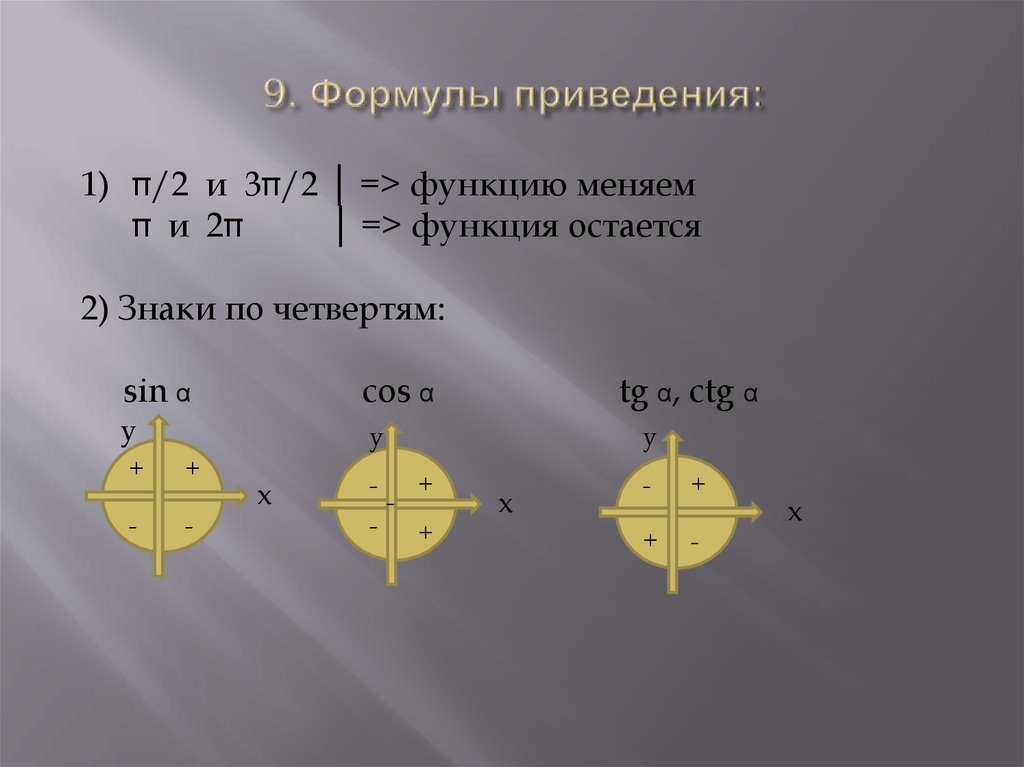
48. 9. Формулы приведения:

1)
/2 и 3 /2 │ => функцию меняем
и 2
│ => функция остается
2) Знаки по четвертям:
sin α
cos α
y
y
+
-
-
+
-
x
-
tg α, ctg α
y
-
+
+
x
-
+
+
-
x

49. Способы решения тригонометрических уравнений.

Метод замены
переменной
Однородные
Метод разложения
на множители

50. Способы решения тригонометрических уравнений.

Метод замены
переменной
Пример:
1) 2sin²x – 5sin x + 2 = 0;
2) cos²x - sin²x – cos x= 0;
3) tg x/2 + 3ctg x/2 = 4;
Однородные
Метод разложения
на множители

51. Способы решения тригонометрических уравнений.

Метод замены
переменной
Пример:
1) 2sin²x – 5sin x + 2 = 0;
2) cos²x - sin²x – cos x= 0;
3) tg x/2 + 3ctg x/2 = 4;
Однородные
Метод разложения
на множители
Пример:
1) (sin x- 1/3) ∙ (cos x+ 2/5) = 0;
2) 2sin x ∙ cos 5x – cos 5x = 0;

52. Способы решения тригонометрических уравнений.

Метод замены
переменной
Пример:
1) 2sin²x – 5sin x + 2 = 0;
2) cos²x - sin²x – cos x= 0;
3) tg x/2 + 3ctg x/2 = 4;
1-ой степени
a ∙ sin x ± b ∙ cos x = 0
1) 2sin x- 3cos x = 0
2) sin 2x + cos 2x = 0
Однородные
Метод разложения
на множители
Пример:
1) (sin x- 1/3) ∙ (cos x+ 2/5) = 0;
2) 2sin x ∙ cos 5x – cos 5x = 0;
2-ой степени
a ∙ sin²x+b ∙ sin x ∙ cos x + c ∙ cos²x = 0
1) sin²x – 3sin x ∙ cos x + 2cos² x = 0
2) √3 sin x ∙ cos x + cos²x = 0
3) sin³x + sin²x ∙ cos x – 3sin x ∙cos² x –
-3cos³x = 0
4) 3sin² 3x – 2√3 sin3x ∙ cos 3x +
+ 5cos² 3x = 2