Преобразование тригонометрических выражений

1. Преобразование тригонометрических выражений

Алгебра - 10 класс
УМК: Н.Г. Мордкович, профильный уровень
Разработала: Богданова Ольга Николаевна, учитель математики
МКОУ «Овечкинская СОШ Завьяловского района»
2015 г.

2. Синус и косинус разности аргументов

sin( x y ) sin x cos y cos x sin y
sin( x y ) sin x cos y cos x sin y
cos( x y ) cos x cos y sin x sin y
cos( x y ) cos x cos y sin x sin y

3. Пример 1

Вычислить : sin 75
sin 75 sin( 30 45 )
sin 30 cos 45 cos 30 sin 45
1 2
3 2
2 2
2 2
2
6
4
4
2 6
4

4. Пример 2

Вычислить : cos15
cos15 cos( 45 30 )
cos 45 cos 30 sin 45 sin 30
2 3
2 1
2 2
2 2
6
2
4
4
6 2
4

5. Пример 3

Вычислить : sin 48 cos12 cos 48 sin 12
sin 48 cos12 cos 48 sin 12
3
sin( 48 12 ) sin 60
2

6. Пример 4

Вычислить : cos(
3
y ), если
II
3
cos y , y
5 2
1
3
cos( y ) cos cos y sin sin y cos y
sin y
3
3
3
2
2
1
3
3 4
( )
3 4 3 3 4 3
2
5
2 5
10
10 10
sin 2 x cos 2 x 1
9
sin 2 x
1
25
9
2
sin x 1
25
16
25
4
sin x
5
sin 2 x

7. Пример 5

Решите уравнение:
sin
3
cos x cos
3
sin(
3
x) cos(
6
x) 3
6
6
sin x cos cos x sin
3
1
3
1
cos x sin x
cos x sin x 3
2
2
2
2
2 3
cos x 3
2
2 3
cos x 3 :
2
cos x 1
x 2 n, n Z
sin x 3

8. Тангенс суммы и разности аргументов

tgx tgy
tg ( x y )
1 tgx tgy
tgx tgy
tg ( x y )
1 tgx tgy

9. Котангенс суммы и разности аргументов

ctgx ctgy 1
ctg ( x y )
ctgx ctgy
ctgx ctgy 1
ctg ( x y )
ctgx ctgy

10. Пример 1

Вычислить : tg 75
tg
30
tg
45
tg 75 tg (30 45 )
1 tg30 tg 45
1 3
1
1
3
1 3
3 1 3 3 1 1 3
3
:
1
3 1
3
3
3
3 1
3 1
1
1
3
3

11. Пример 2

II
3
Вычислить : tg ( x), если cos x , x
5 2
4
tgx
4
4
1
1 tgx
4
1
3 3 7
tg ( x)
: ( ) 7
4
1
1
tgx
4
3
3
1 tg tgx
1
3
3
4
sin 2 x cos 2 x 1
9
2
sin x
1
25
9
sin 2 x 1
sin x
4
3
4
25
tgx
: ( )
tg
16
sin x
25
4
sin x
5
2
1
cos x
5
5
3

12. Формулы приведения

2
3
2
sin
cos
sin
cos
sin
cos
sin
cos
sin
cos
tg
ctg
tg
ctg
tg
ctg
tg
ctg
tg
ctg
2

13. Пример 1

Вычислить : cos(
2
1
cos( 30 ) sin 30
2
2
30 )

14. Пример 2

Вычислить : tg (180 )
4
tg (180 ) tg 1
4
4

15. Пример 3

Вычислить : sin( 2 45 )
2
sin( 2 45 ) sin 45
2

16. Пример 4

Вычислить : ctg (270 60 )
ctg (270 60 ) tg 60 3

17. Формулы двойного аргумента

sin 2x 2 sin x cos x cos 2 x cos x sin x
2
2tg x
tg 2 x
1 tg 2 x
2
ctg x 1
ctg 2 x
2ctgx
2

18. Пример 1

Доказать тождество : 1 sin 2 x (cos x sin x) 2
Л.ч. 1 sin 2x sin 2 x cos 2 x 2 sin x cos x
sin 2 x 2 sin x cos x cos 2 x (sin x cos x) 2 П.ч.

19. Пример 2

1
sin
2
x
дробь
:
Сократить
cos 2 x
2
2
sin
x
cos
x 2 sin x cos x
1 sin 2 x
2
2
cos 2 x
cos x sin x
(sin x cos x)
sin x cos x
(cos x sin x) (cos x sin x)
cos x sin x
2

20. Пример 3

Вычислить : cos
cos
2
8
sin
2
2
8
sin
2
8
cos( 2 ) cos
8
8
4
2
2

21. Пример 4

Доказать тождество :
2
tgx ctgx
sin 2 x
sin x cos x sin x cos x
Л .ч. tgx ctgx
cos x sin x
cos x sin x
2
2
1
2
2
П.ч.
cos x sin x 2 cos x sin x sin 2 x

22. Пример 5

Зная, что сosx 3 , x 3 ;2 , вычислить cos 2 x :
5
2 IV
2
2
3
4
сos2x cos x sin x 9 16 7
25
25 25
5 5
sin 2 x cos 2 x 1
2
9
1
25
9
2
sin x 1
25
sin 2 x
16
25
4
sin x
5
sin
2
x
2

23. Пример 6

Решите уравнение : sin 4 x cos 2 x 0
sin 4x cos 2x 0
2 sin 2x cos 2x cos 2x 0
cos 2 x(2 sin 2 x 1) 0
2 x ( 1) arcsin
cos 2x 0 или 2 sin 2x 1 0
n, n Z
2 n
x ,n Z
4 2
2x
2 sin 2x 1 0
2 sin 2x 1
1
sin 2 x
1 2
k
k , k Z
2
k
2 x ( 1)
k , k Z
6
k
x ( 1) k
,k Z
12 2

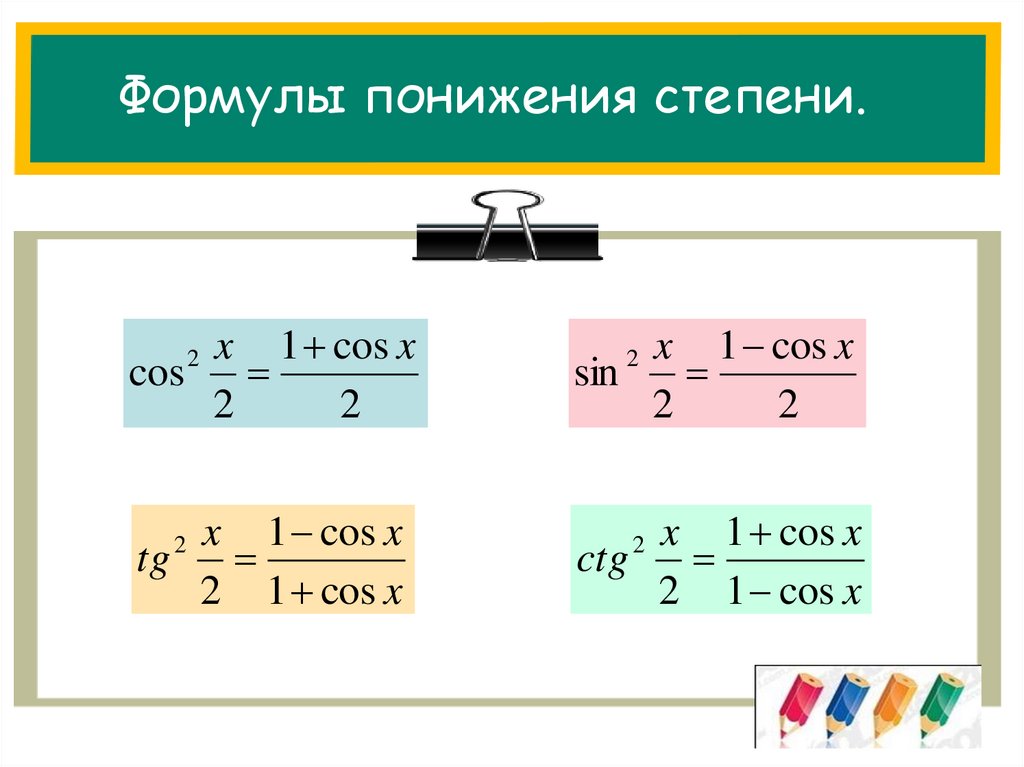
24. Формулы понижения степени.

x 1 cos x
cos
2
2
x 1 cos x
sin
2
2
x 1 cos x
tg
2 1 cos x
x 1 cos x
ctg
2 1 cos x
2
2
2
2

25. Пример 1

5
x
, x ; , вычислите cos
Зная, что cos x
13
2
2 II
5
1
8
8 1
4
x
1
cos
x
2
13
:2
cos
13
13 2
13
2
2
2
x
cos
2
4
13
x
cos 2
2
13

26. Пример 2

3
Решите уравнение : cos 3x Т .к. cos 2 3x 1 cos 6 x , то
4
2
1 cos 6 x 3
1
cos 6 x
2
4
2
1
4(1 cos 6 x) 6
6 x arccos 2 n, n Z
2
3
6 x 2 n, n Z
1 cos 6 x
3
2
n
x ,n Z
3
18 3
cos 6 x 1
2
2

27.

Разложение суммы и разности на
множители
sin x sin y 2 sin x y cos x y
2
2
x y
x y
sin x sin y 2 sin
cos
2
2
x y
x y
cos x cos y 2 cos
cos
2
2
x y
x y
sin
cos x cos y 2 sin
2
2

28.

Пример 1
Решите уравнение : sin 5 x sin x 0
5x x
5x x
cos
0
2
2
2 sin 3x cos 2x 0
2 sin
sin 3x cos 2x 0
sin 3x 0
3x n, n Z
n
x ,n Z
3
или
cos 2x 0
2 x n, n Z
2
т
x
,n Z
4 2

29.

Пример 2
Решите уравнение : sin x sin 2 x sin 3x 0
(sin x sin 3x) sin 2 x 0
x 3x
x 3x
cos
sin 2x 0
2
2
2 sin 2x cos x sin 2x 0
sin 2 x(2 cos x 1) 0
или
2 cos x 1 0 x arccos 1 2 n, n Z
sin 2x 0
2
2 x n, n Z
2 cos x 1
2
1
x
2 n, n Z
n
cos
x
3
x ,n Z
2
2
2 sin

30.

Пример 3
Решите уравнение :
cos 2 x sin 2 3x 1
1 cos 2 x 1 cos 6 x
1
2
2
1 cos 2 x 1 cos 6 x
1
2
2 cos 2 x cos 6 x
1
2
2 cos 2x cos 6x 2
cos 2x cos 6x 0
2 sin
2x 6x
2x 6x
sin
0
2
2
2 sin 4 x sin( 2 x) 0
2 sin 4x sin 2x 0
sin 4x sin 2x 0
sin 4x 0
4 x n, n Z
n
x ,n Z
4
или
sin 2x 0
2 x n, n Z
n
x ,n Z
2

31.

Формулы представления
произведения в виде суммы
cos( x y ) cos( x y )
sin x sin y
2
cos( x y ) cos( x y )
cos x cos y
2
sin( x y ) sin( x y )
sin x cos y
2

32.

Пример 1
Преобразуйте произведение в сумму sin 5x cos 3x
sin 8 x sin 2 x
sin( 5 x 3x) sin( 5 x 3x)
sin 5x cos 3x
2
2

33.

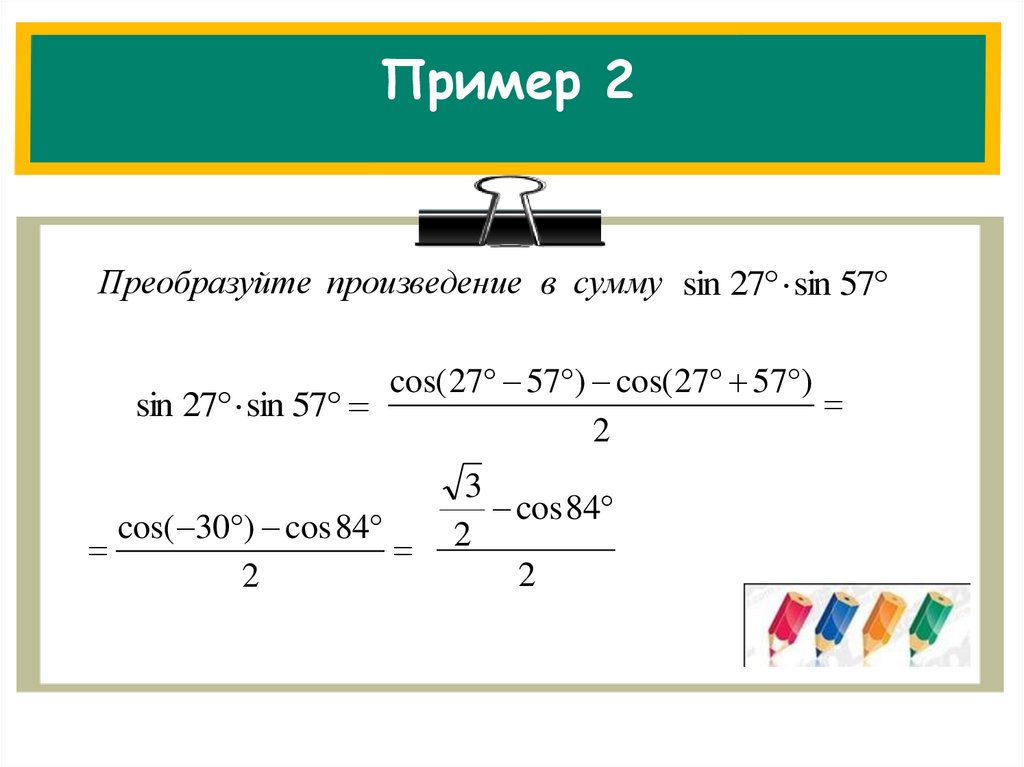
Пример 2
Преобразуйте произведение в сумму sin 27 sin 57
cos( 27 57 ) cos( 27 57 )
sin 27 sin 57
2
cos( 30 ) cos 84
2
3
cos 84
2
2

34.

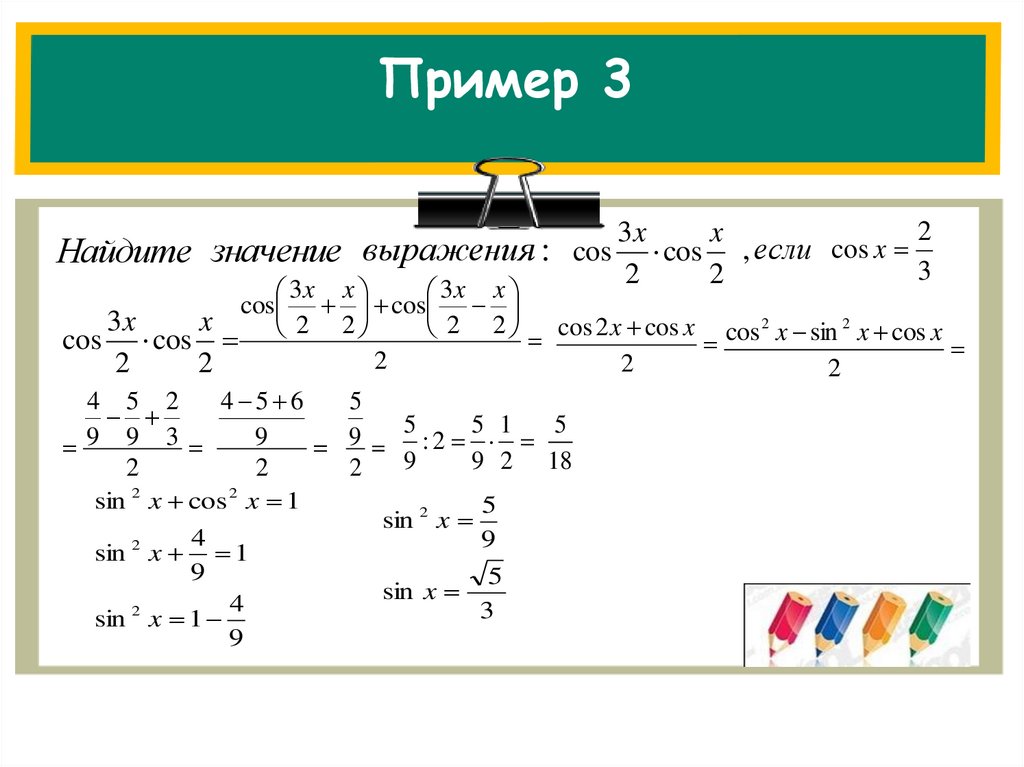
Пример 3
Найдите значение
выражения : cos
2
3x
x
cos , если cos x
3
2
2
3x x
3x x
cos cos
3x
x
2 2
2 2 cos 2 x cos x cos 2 x sin 2 x cos x
cos cos
2
2
2
2
2
4 5 2
4 5 6
5
5
5 1
5
9
9
3
9
9
:
2
9
9 2 18
2
2
2
sin 2 x cos 2 x 1
4
1
9
4
sin 2 x 1
9
sin 2 x
5
9
5
sin x
3
sin 2 x

35. Преобразование выражения Asinx+Bcosx к виду Csin(x+t)

Asin x B sin x С sin( x t )
Asin x B sin x С cos( x t ), где
С
t вспомогательный аргумент
A B
2
2

36.

Пример 1
Преобразуйте в произведение 5 sin x 12 cos x
A 5, B 12,
5 sin x 12 cos x 13(
Пусть
тоC 25 144 169 13
5
12
sin x cos x) 13(cos t sin x sin t cos x)
13
13
5
12
cos t , sin t
13
13
13 sin( x t )
где
t arcsin
12
13

37.

Пример 2
Найдите наибольшее и наименьшее значение функции
y 5 sin x 12 cos x
Все выполнить как в предыдущем примере
y 13 sin( x t )
ymax 13
ymin 13

38.

Пример 3
Решите уравнение : 5 sin x 12 cos x 13
13 sin( x t ) 13
5 sin x 12 cos x 13 sin( x t )
sin( x t ) 1
x t
x t
t ark sin
12
13
2
2
2 n, n Z
2 n, n Z
12
x ark sin
2 n, n Z
13 2

39.

Пример 3
Источники
- А.Г. Мордкович Алгебра – 10, профильный уровень, часть 1 – учебник, М:
Мнемозина, 2013
- А.Г. Мордкович и др., Алгебра – 10, профильный уровень, часть 2 –
задачник, М: Мнемозина, 2013
- А.Г. Мордкович, П.В. Семенов. Методическое пособие для учителя, «Алгебра
и начала анализа», профильный уровень, 10 класс, «Мнемозина», М. 2013.
- http://ru.clipartlogo.com/free/pencil.html - картинка карандашей