Похожие презентации:
Арифметическая прогрессия. Урок 3
1.
16.01.12Классная работа
2.
Выявите закономерность и задайтепоследовательность рекуррентной формулой
1) 1, 2, 3, 4, 5, …
2) 2, 5, 8, 11, 14,…
3) 8, 6, 4, 2, 0, - 2, …
4) 0,5; 1; 1,5; 2; 2,5; …
an 1 an 1
an 1 an 3
an 1 an ( 2)
an 1 an 0,5
an 1 an d
3. Арифметическая прогрессия
4.
Определение арифметическойпрогрессии
Арифметическая прогрессия – это числовая
последовательность, каждый член которой,
начиная со второго равен предыдущему
сложенному с одним и тем же числом.
an 1 an d
разность арифметической прогрессии
d -(число)
5.
Определение арифметическойпрогрессии
a1 , a2 , a3 ,..., an ...- арифметическая
прогрессия, если для всех натуральных n
выполняется равенство
an 1 an d
6.
Разность арифметическойпрогрессии
d an 1 an
d 0
d 0
- прогрессия возрастающая
- прогрессия убывающая
7.
Назвать первый член и разностьарифметической прогрессии:
1) 6, 8, 10, 12, …
a1 6
d 2
2) 7, 10, 13, 16, …
a1 7
d 3
3) 25, 21, 17, 13, …
a1 25 d 4
4) -12, -9, -6, -3, …
a1 12 d 3
8.
Запишите первые пять членоварифметической прогрессии, если
1)
a1 7 , d 5
Ответ: 7; 12; 17; 22; 27
2)
a1 11, d 2
Ответ: 11; 9; 7; 5; 3
9.
Доказать, что последовательность,заданная формулой an 3 4n , является
арифметической прогрессией
Требуется доказать, что разность an 1
и та же для всех n ( не зависит от n )
an
an 1 3 4(n 1)
an 1 an 3 4(n 1) (3 4n)
3 4n 4 3 4n 4
одна
10.
Задание арифметической прогрессииформулой n –го члена
a1 первый член арифметической прогрессии
d разность арифметической прогрессии
a2 a1 d
a3 a2 d (a1 d ) d a1 2d
a4 a3 d (a1 2d ) d a1 3d
a5 a4 d (a1 3d ) d a1 4d
an a1 (n 1) d
11.
№ 236 (2, 4)an a1 (n 1) d
a1 3 d 4
a1 2 d 4
a20 3 (20 1) 4
a11 2 (11 1) ( 4)
a20 3 19 4 79
a11 2 10 ( 4) 42
12.
№ 237 (2)Записать формулу n –го члена арифметической
прогрессии: 25; 21; 17; 13 …
Решение:
a1 25
a2 21
d a2 a1
d 21 25 4
an a1 (n 1) d
an 25 (n 1) ( 4) 25 4n 4 29 4n
Ответ : an 29 4n
13.
№ 237 (4)Записать формулу n –го члена арифметической
прогрессии: 1; -4; -9; -14 …
Решение:
a1 1
a2 4
d a2 a1
d 4 1 5
an a1 (n 1) d
an 1 (n 1) ( 5) 1 5n 5 6 5n
Ответ : an 6 5n
14.
Свойство n –го члена арифметическойпрогрессии
Каждый член арифметической прогрессии,
начиная со второго, равен среднему
арифметическому двух соседних с ним членов
an 1 an 1
an
2
15.
Выписаны несколько последовательныхчленов арифметической прогрессии:
-34; -18; х; 14; …
Найдите член прогрессии обозначенный
буквой х.
Решение:
an 1 an 1
an
2
18 14
х
2
2
16.
Подведем итогАрифметическая прогрессия – это числовая
последовательность, каждый член которой,
начиная со второго равен предыдущему
сложенному с одним и тем же числом.
an 1 an d
d - разность арифметической прогрессии
(число)
17.
Подведем итогd - разность арифметической прогрессии
(число)
d an 1 an
Формула n-го члена арифметической
прогрессии
an a1 (n 1) d
18.
Подведем итогСвойство n –го члена арифметической
прогрессии
Каждый член арифметической прогрессии,
начиная со второго, равен среднему
арифметическому двух соседних с ним членов
an 1 an 1
an
2
19.
Домашнее задание:•Читать параграф 18, учить правила.
•Уметь выводить формулу n – го члена
арифметической прогрессии и свойство n – го
члена арифметической прогрессии.
•№ 234, № 236 (1,3), № 237 (1,3)
20.
Последовательности заданы несколькимипервыми членами. Одна уз них –
арифметическая прогрессия. Укажите ее.
А) 1; 4; 9; 16; …
Б) -3; -6; -9; -12; …
В) 1; 3; 9; 27; …
21.
Какая из последовательностей являетсяарифметической прогрессией?
А) последовательность натуральных степеней числа 2
Б) последовательность чисел, обратных натуральным
В) последовательность квадратов натуральных чисел
С) последовательность натуральных чисел, кратных 7
22.
Для каждой арифметической прогрессии,заданной формулой n – го члена укажите ее
разность d
A)an 4n 3
1)d 2
Б )bn 2n 4
2) d 4
B)cn 3n 2
3)d 2
4) d 3










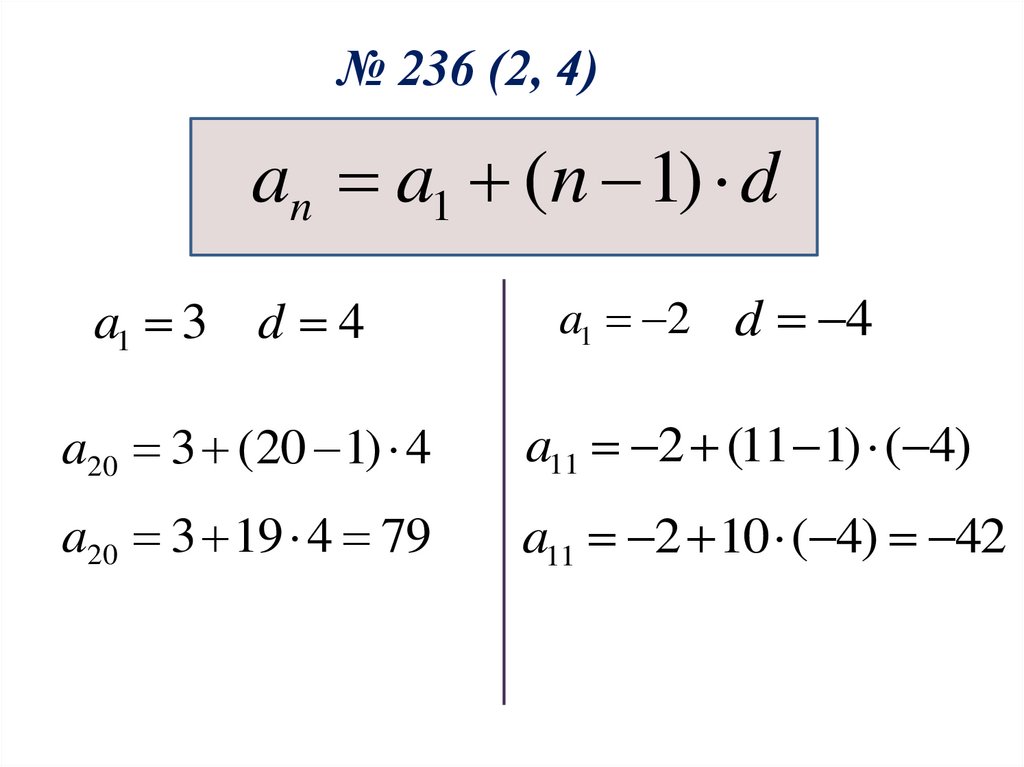











 Математика
Математика








