Похожие презентации:
Свойства логарифмов
1.
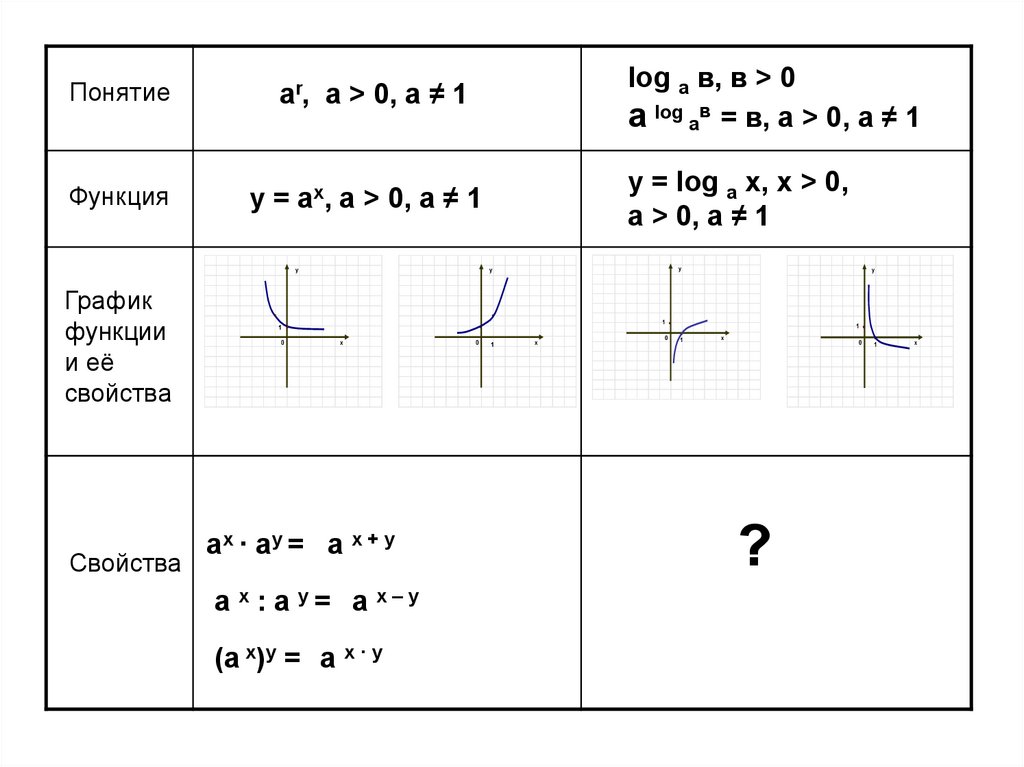
ПонятиеФункция
log a в, в > 0
а log aв = в, а > 0, а ≠ 1
аr, а > 0, а ≠ 1
у
График
функции
и её
свойства
Свойства
у = log a х, х > 0,
а > 0, а ≠ 1
у = ах, а > 0, а ≠ 1
у
у
у
1
1
0
х
а х · ау = а х + у
а х : а у= а х–у
(а х)у = а х · у
0
1
х
1
0
1
х
0
?
1
х
2.
Свойства логарифмов(показателей)
3.
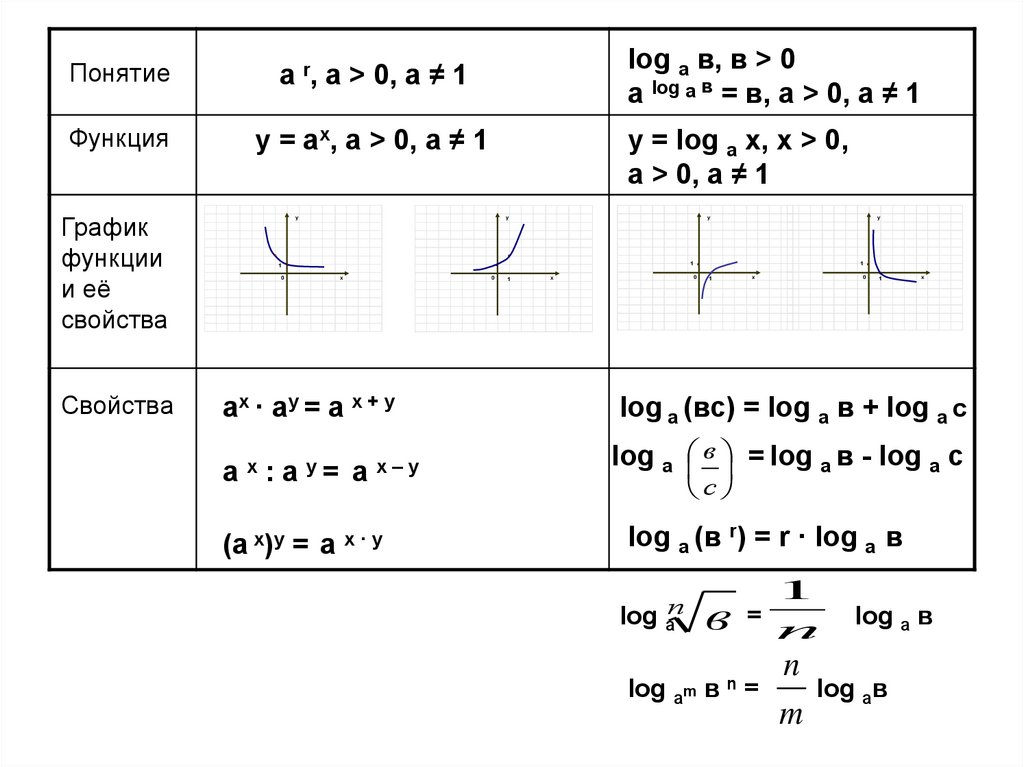
Понятиеа r, а > 0, а ≠ 1
Функция
у = ах, а > 0, а ≠ 1
График
функции
и её
свойства
Свойства
log a в, в > 0
а log a в = в, а > 0, а ≠ 1
у = log a х, х > 0,
а > 0, а ≠ 1
у
у
у
у
1
1
х
0
0
1
х
1
0
х
1
0
1
х
ах · ау = а х + у
log а (вс) = log а в + log а с
а :а
log а в = log а в - log а с
х
у=
а
х–у
(а х)у = а х · у
с
log а (в r) = r · log а в
log ап
в
1
=
п
log аm в =
n
n
m
log а в
log aв
4.
Из словаря Даля:ЛОГАРúӨМЪ м. матем. Если подъ
рядомъ чиселъ геометрической прогресiи
(лѣствицы) выставить рядъ отвѣчающих
имъ чиселъ ариөметической прогресiи, то
каждое изъ послѣднихъ будетѣ
логариөмомъ дрýжки своей, въ первомъ
порядкѣ; симъ способомъ умноженiе
обращаютъ въ сложенiе, дѣленiе въ
вычитанье, что и облегчаетъ выкладки.
Логариөмùческiй, къ логариөмамъ
относящiйся. Логарùөмика ж. кривая
линiя, въ коей ординаты отвѣчают
логариөмамъ абсцисъ; логùстика.


 Математика
Математика








