Модуль числа

1.

Буланникова Н.В
Учитель математики
МБОУ СОШ № 4
г. Салехард

2. Наши цели:

Наши задачи:

3. Как свойства модуля помогают решать уравнения

Ошибочное решение :
| 2х – 3 | = 5
2х – 3 = 5
х=4
|f(x)|= a
f(x) = ±a
Верное решение:
| 2х – 3 | = 5
2х – 3 = - 5
2х – 3 = 5
х=-1
х=4
Вывод: Если не использовать свойство модуля ,то
тогда, решая уравнение 1 способом, мы теряем
один из корней уравнения.
Следовательно ПРИ РЕШЕНИИ УРАВНЕНИЙ вида
|f(x)| = а необходимо учитывать, что под знаком
модуля может стоять, как положительная, так и
отрицательная величина.

4. Как свойства модуля помогают решать уравнения

Верное решение:
| 4 + 3х | = 2х – 1
| 4 + 3х | = 2х – 1
ОДЗ: 2х – 1 ≥ 0, х ≥ 0,5
4 + 3х = 1 – 2х
х = - 0,6
или
4 + 3х = 2х – 1
х=-5
Ответ: - 5; - 0,6.
4 + 3х = 1 – 2х или 4 + 3х = 2х – 1
х = - 0,6
х=-5
Ответ: х ϵ Ø
Вывод:ПРИ РЕШЕНИИ УРАВНЕНИЙ
вида |f(x)| = g(x)
необходимо учитывать условие : g(x) ≥ 0

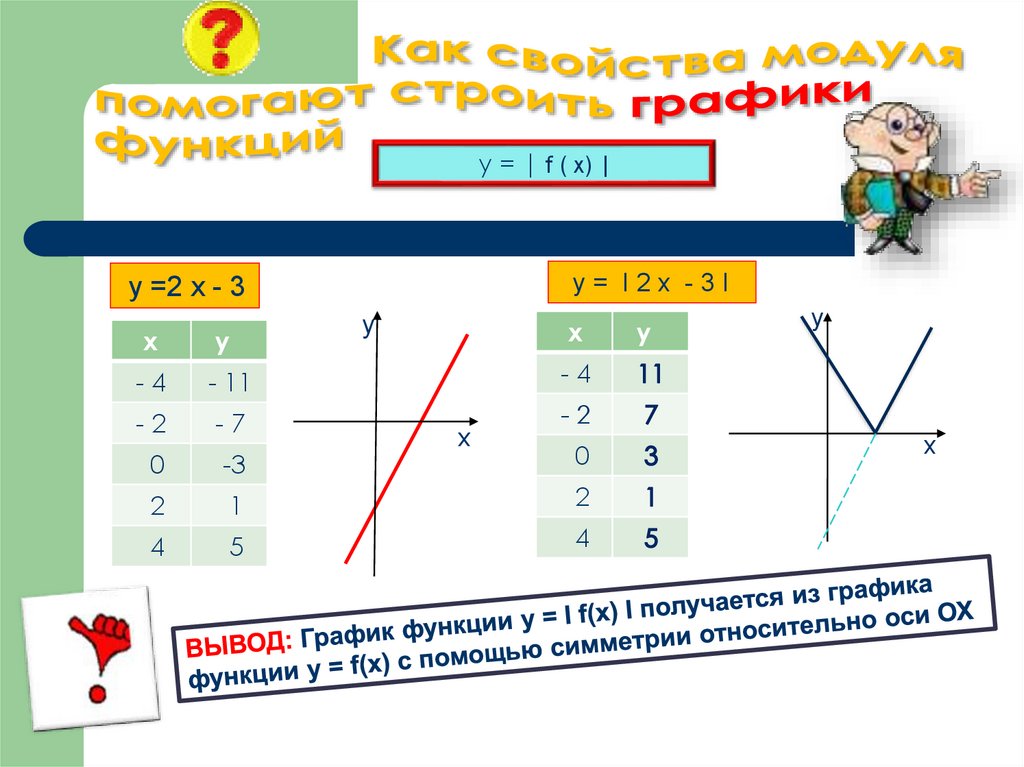
5. Как свойства модуля помогают строить графики функций

у = | f ( x) |
y= I2x -3I
y =2 x - 3
y
x
x
y
-4
- 11
-4
-2
-7
-2
x
0
0
-3
2
1
2
4
5
4
y
у
х

6. Как свойства модуля помогают строить графики функций

y = f( IxI )
y =2x - 3
y
y=2IxI-3
x
y
x
y
-4
-11
-4
5
-2
- 7
-2
1
0
-3
0
-3
2
1
2
1
4
5
4
5
x
y
x

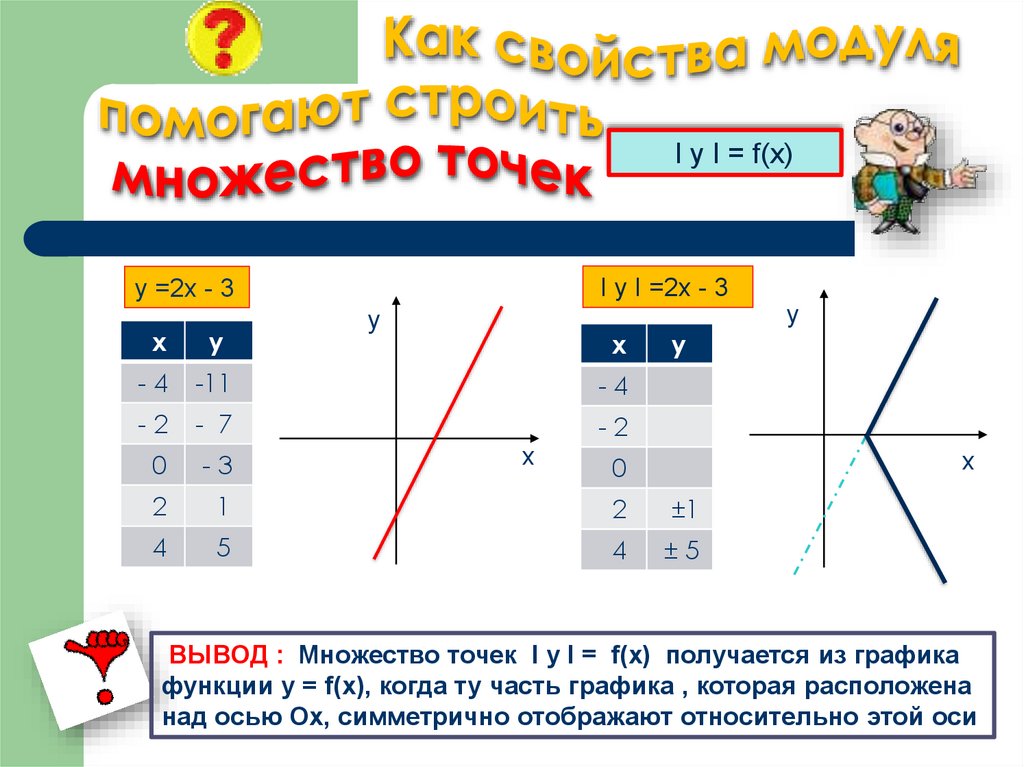
7. Как свойства модуля помогают строить множество точек

I y I = f(x)
I y I =2x - 3
y =2x - 3
y
x
y
-4
-11
-4
-2
- 7
-2
0
-3
2
1
2
±1
4
5
4
±5
x
x
y
y
x
0
ВЫВОД : Множество точек I у I = f(x) получается из графика
функции у = f(x), когда ту часть графика , которая расположена
над осью Ох, симметрично отображают относительно этой оси

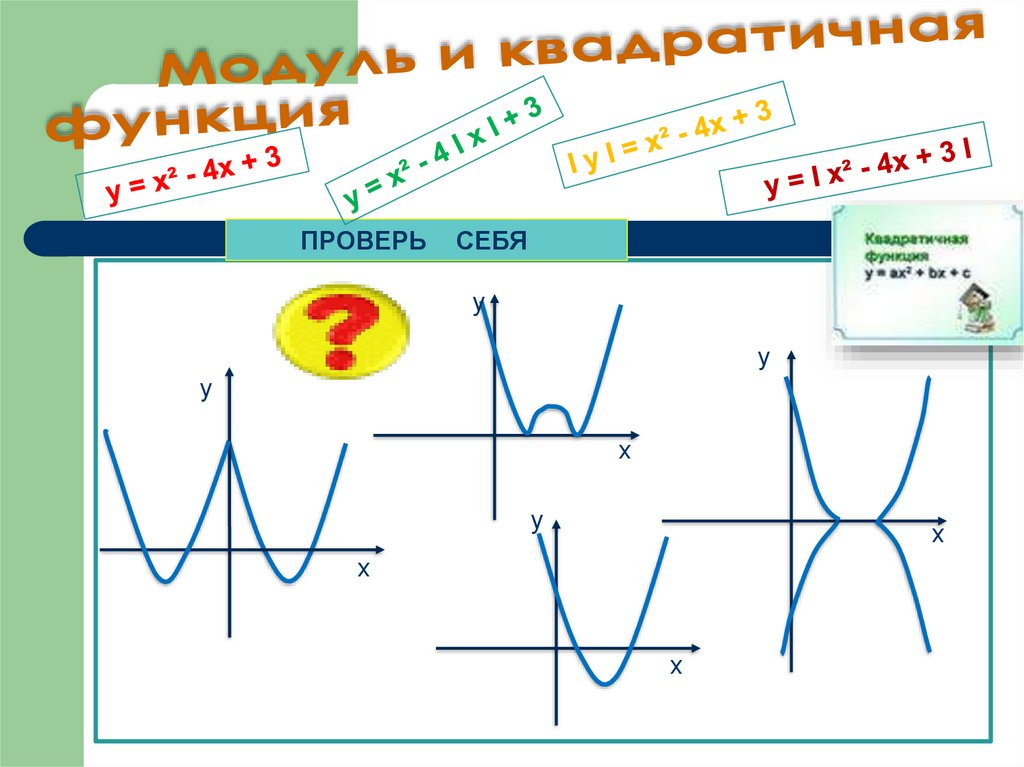
8. Модуль и квадратичная функция

ПРОВЕРЬ
СЕБЯ
y
y
y
x
y
x
x
x

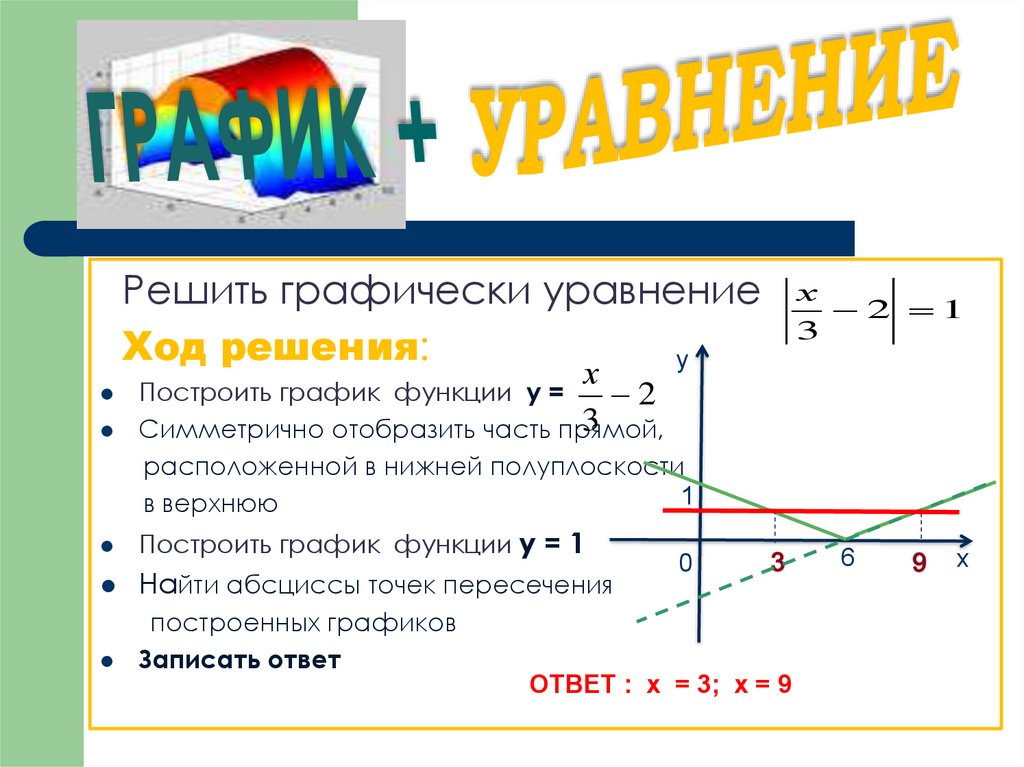
9. ГРАФИК + УРАВНЕНИЕ

Решить графически уравнение
Ход решения:
у
х
2 1
3
х
Построить график функции у =
2
3
Симметрично отобразить часть прямой,
расположенной в нижней полуплоскости
1
в верхнюю
Построить график функции у = 1
Найти абсциссы точек пересечения
построенных графиков
Записать ответ
0
ОТВЕТ : х = 3; х = 9
6
х

10. ПРОВЕРЬ СЕБЯ

│3lхl - 5│= х + 1
О.Д.З : х ≥ - 1
3 lхl – 5 = х + 1
3 lхl – 5 = – х – 1,
3 lхl = х + 6
х≥-6
3х = - х – 6
3х = х + 6.
| 3ІxІ
- 5- 5| =
| 3ІxІ
| =xx++ 11
3 lхl = 4 – х
х≤4
3х = х – 4
3х = 4 - х
| 3ІxІ
- 5 |: =х ≥x- +1 1
О.Д.З
Х = - 1,5
Х=3
Ответ: 1; 3
2 корня
Х=-2
Х=1