Похожие презентации:
Модуль действительного числа (пн – вт)
1. 14.09.20 г.
Модуль действительногочисла
(пн – вт)
2. Определение
Абсолютной величиной (модулем)неотрицательного действительного числа
а называют само это число: |а|=а; модулем
отрицательного действительного числа а
называют противоположное число: |а|=-а.
a , если а 0;
a
а , если а 0.
Пример:
2x 3, если x 1,5;
2x 3
2x 3, если x 1,5.
3. Свойства модуля
1 a а2 a b а b
а
a
3
, где b 0
b
b
4 a b а b , если a 0, b 0
5 a b a b, если a 0, b 0
4. Свойства модуля
6 a b а b , если ab 07 a
2
a
2
8 a b 0, если a b 0
2
9
2
a а
2
10 a1 a2 ... an а1 а2 ... аn
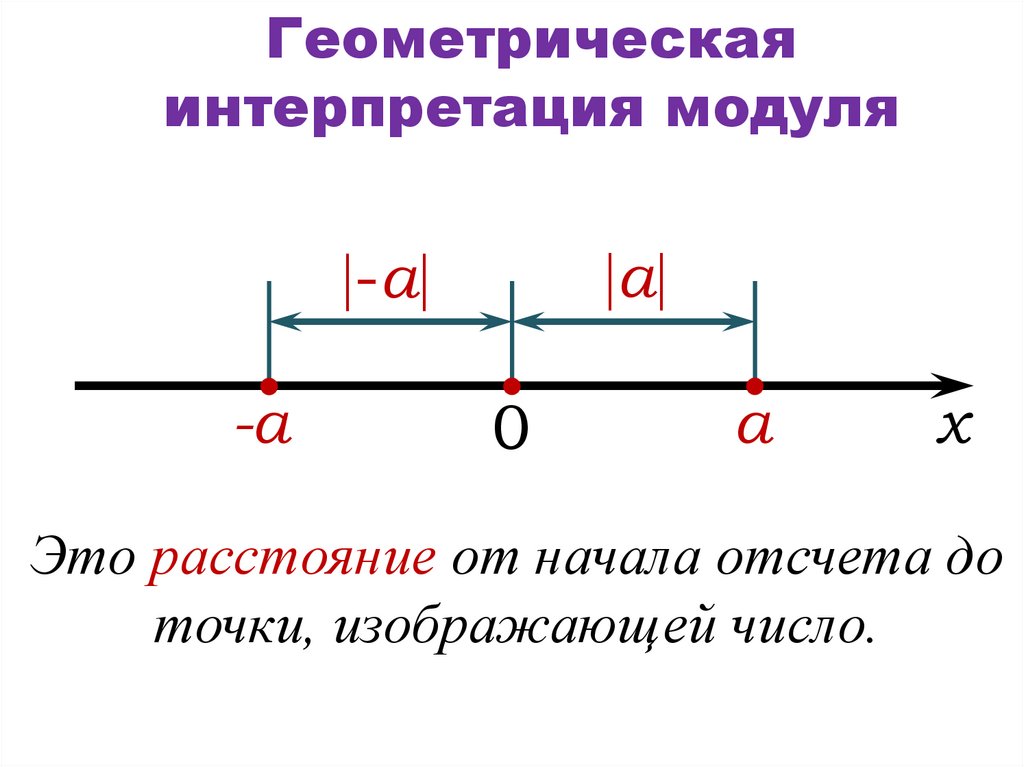
5. Геометрическая интерпретация модуля
а-а
-а
0
а
х
Это расстояние от начала отсчета до
точки, изображающей число.
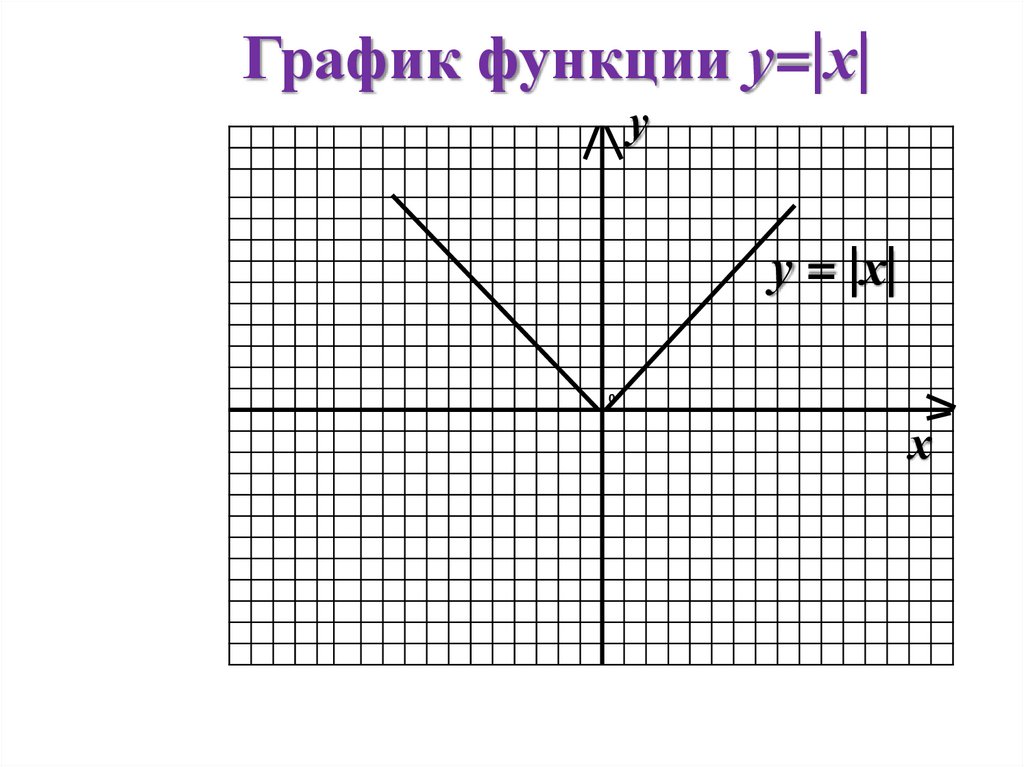
6. График функции у=|х|
уу = |х|
0
х
7. №1*. Раскрыть модули:
1) p 3 ;2)
3 5;
3)
5 2;
4) 1 2 ;
5) x 2 ;
6) x 1 ;
4
7) ( a 3 ) , a 3 ;
2
8) ( b 4 ) , b 4 ;
2
9) m 2m 1,
2
m 1.
8. Решение уравнений вида f (x) = a
Решение уравнений видаf (x) = a
f (x ) a ,
f (x ) a.
Пример: x – 8 = 5
x 8 5,
x 8 5; ⇔
Ответ: 3; 13.
x 13,
x 3.
9. №2*. Решение уравнений вида |f (x)|= a
1) |2x – 3|= 42) |5x + 6|= 7
3) |9 – 3x |= 6
4) |4x + 2|= – 1
5) |8 – 2x|= 0
6) |10x + 3|= 16
7) |24 – 3x|= 12
8) |2x + 30|= 48
x1 = 3,5;
x1 = 0,2;
x1 = 1;
x Ø
x=4
x1 = 1,3;
x1 = 12;
x1 = 9;
x2 = – 0,5
x2 = – 2,6
x2 = 5
x2 = – 1,9
x2 = 4
x2 = – 39
10.
Решение уравнений видаf(x) = g(x)
f (x ) g (x ),
g
(
x
)
0
;
f (x ) g (x ),
g (x ) 0.
или
f (x ) g (x ),
f (x ) g (x ),
g (x ) 0;
11. Пример: 3х –10 = х – 2
Пример: 3х –10 = х – 23x 10 x 2,
x
2
0
;
3x 10 (x 2),
x 2 0;
x 4,
⇔
x 3.
Ответ: 3; 4.
⇔
2x 8,
x
2
;
4x 12,
x 2;
⇔
12.
Решение уравнений видаf(x) = g(x)
f (x ) g (x ),
f (x ) g (x ).
Пример: x – 2 = 3 – x
x 2,5,
2x 5,
x 2 3 x ,
⇔
⇔
x Ø ;
x 2 3 x ;
2 3;
Ответ: 2,5.
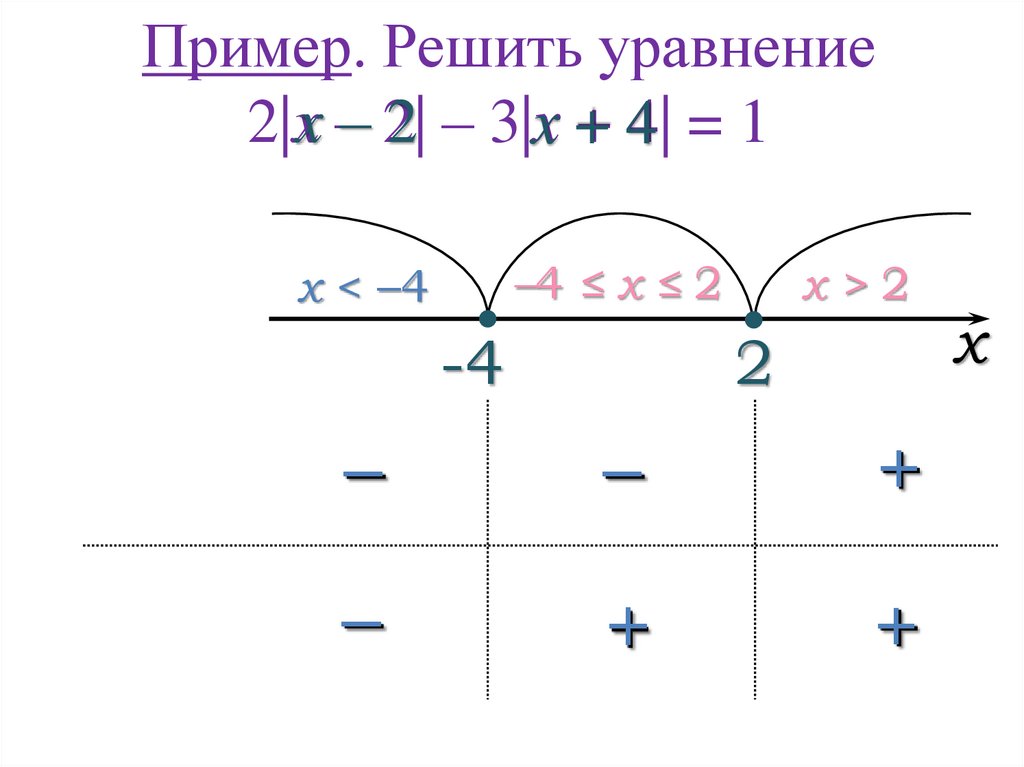
13. Пример. Решить уравнение 2|x – 2| – 3|х + 4| = 1
Пример. Решить уравнение2 – 3|хx + 44| = 1
2|xx – 2|
–4 ≤ x ≤ 2
x < –4
-4
x>2
2
–
–
+
–
+
+
х
14.
x 4,2( x 2) 3( x 4) 1;
4 x 2,
2( x 2) 3(x 4) 1;
x 2,
2(x 2) 3(x 4) 1;
Ответ: –15; –1,8.
⇔
x 4,
x 15;
4 x 2,
x 1,8;
x 2,
x 17.
15. №3*. Решить самостоятельно
2x
1) + 3x = 2(x + 1)
2
2) x – 6 = x – 5x + 9
3) 2x + 8 – x – 5 = 12
1) Ответ: 1; (–5 + √17)/2.
2) Ответ: 1; 3.
3) Ответ: 3
16. Пример. Решить неравенство |x – 2| + |х + 8| ≤ 4х + 4
Пример. Решить неравенство+88| ≤ 4х + 4
|xx – 22| + |хx +
–8 ≤ x ≤ 2
x < -8
-8
x>2
2
–
–
+
–
+
+
х
самостоятельно …
17.
На уроке:1) Новая тема №1* - 3*, примеры…
2) №5.9, 5.10 (в, г), 5.11 (б, в), 5.12 (а), 5.14 (а, в), 5.15 (в,
г), 5.16 (б, г), 5.17 (б, г),
3) С-5 – 15 минут (вторник)
Дома: (на вторник)
1) Теорию наизусть
2) №5.1 – 5.3, 5.10 (а, б), 5.11 (а, г), 5.13, 5.18 (б)
Дома: (на среду)
1) Теорию повторять, подг. к к/р.
2) №5.14 (а, в), 5.15 (а, б), 5.16 (а, в), 5.17 (а, в), 5.18 (а)








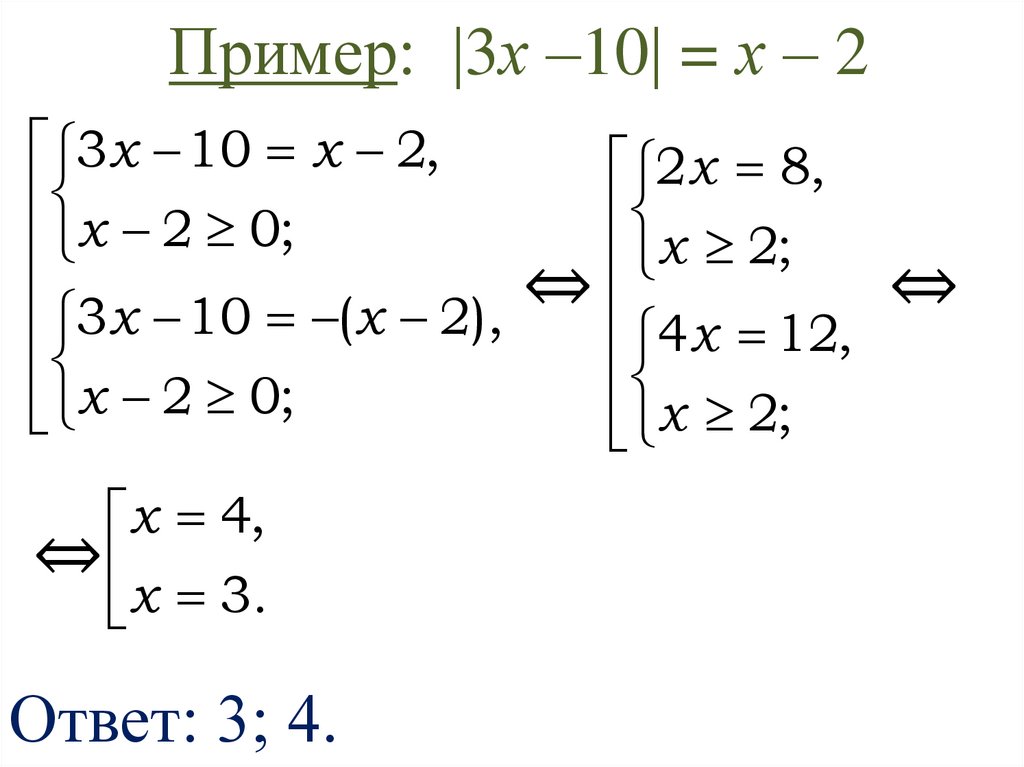

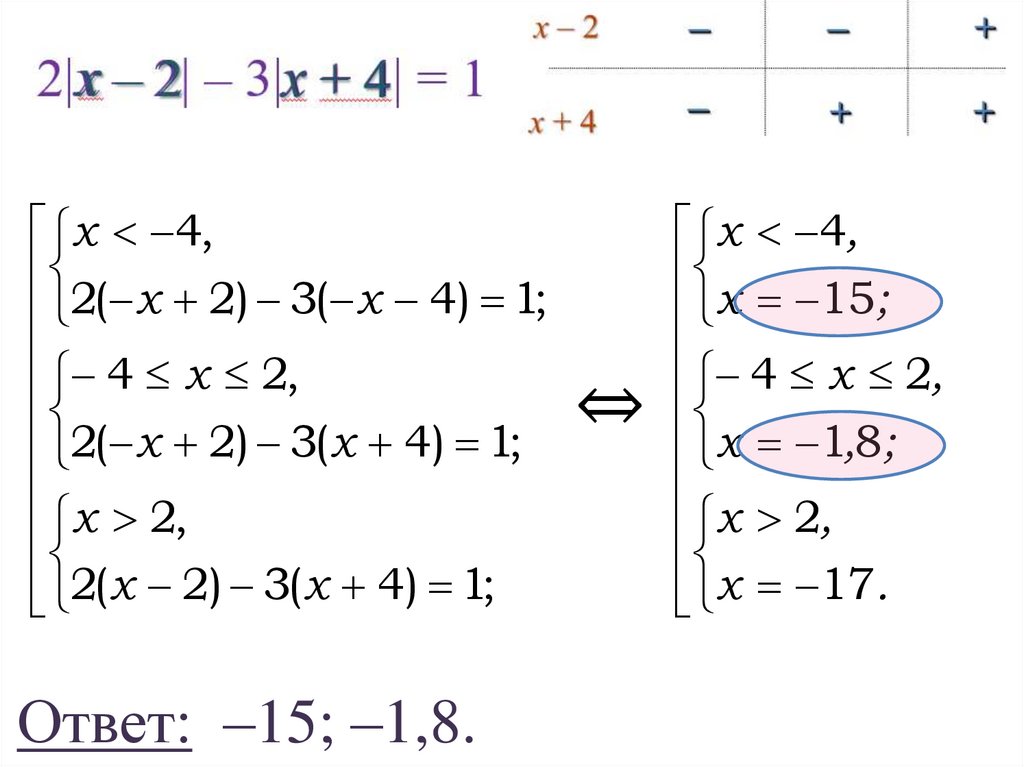



 Математика
Математика








