Похожие презентации:
Свободные электрические колебания. Электричество и магнетизм
1.
§ 34 Свободные электрические колебанияГлава 3
Электричество и магнетизм
2.
Вконтуре, содержащем емкость и
индуктивность могут возникнуть колебания.
Причина – явление самоиндукции.
UC S
q
dI
L
c
dt
q
Lq
c
3.
Дифференциальное уравнение гармоническихколебаний.
1
q
q 0
LC
Решение уравнения – гармоническая функция.
q q0 cos t 0
4.
Циклическаячастота
и
период
колебаний
определяются емкостью и индуктивностью.
1
LC
T 2 LC
5.
Открытый колебательный контур резонирует наэлектромагнитную волну длиной :
c
cT 2 c LC
6.
Максимальные энергии катушки и емкости равны.2
0
LI
CU
2
2
2
0
В любой момент времени согласно закону сохранения
энергии существует равенство
2
2
CU
LI
CU
2
2
2
2
0
7.
Время распространения сигнала по цепиl
c
Квазистационарность
означает,
что
сила
тока
одинакова во всех участках неразветвленной цепи.
Следовательно, необходимо выполнение условия
T
8.
§ 35 Затухающие электрические колебанияГлава 3
Электричество и магнетизм
9.
Рассмотрим цепь, содержащую емкость, индуктивностьи сопротивление. При разрядке конденсатора
происходят затухающие колебания. Применяя правило
Кирхгофа, запишем
U R UC S
q
IR Lq
C
10.
Преобразуем уравнениеR
q
q q
0
L
LC
R
1
q 2
q
q 0
2L
LC
11.
Получили дифференциальное уравнение затухающихколебаний.
q 2 q 0 q 0
2
R
2L
0
1
LC
Коэффициент затухания
Собственная циклическая частота
колебаний
12.
Решением является уравнение затухающих колебанийq q0e
t
cos t 0
Циклическая частота колебаний
2
0
2
13.
Амплитуда заряда на конденсаторе убывает поэкспоненциальному закону
q t q0e
t
Полная энергия контура
W t W0e
2 t
14. Рассмотрим основные величины, характеризующие затухающие колебания.
1. Период колебанийT
2
2
0
2
15.
Апериодические колебания возникнут при условии0
R
1
LC 2 L
L
R 2
C
16.
2. Время релаксации – время в течение которогоамплитуда заряда уменьшается в е раз.
1
2L
R
17.
3. Логарифмический декремент затухания равенлогарифму отношения амплитуд колебаний через
период
A t
R
ln
T
A T t
L
C
T0 R
L
при малом затухании
18.
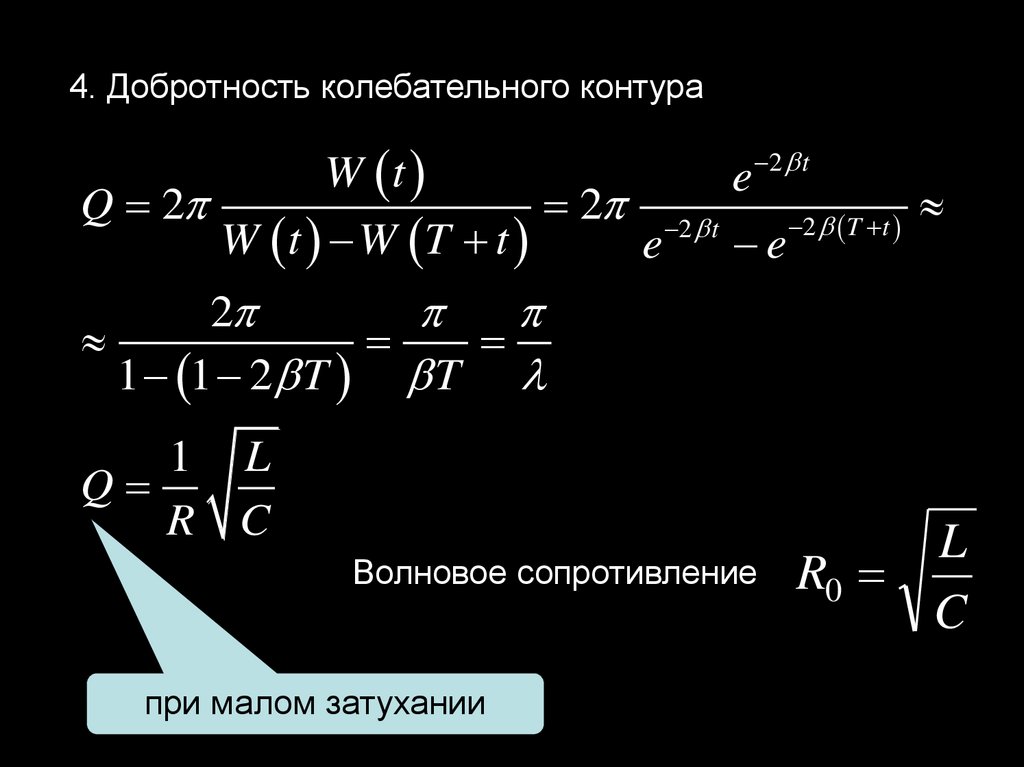
4. Добротность колебательного контураW t
e 2 t
Q 2
2 2 t
2 T t
W t W T t
e
e
2
1 1 2 T T
1 L
Q
R C
Волновое сопротивление
при малом затухании
L
R0
C
19.
§ 36 Вынужденные электрическиеколебания. Законы переменного тока
20. Для поддержания незатухающих колебаний цепь должна находиться под внешним переменным напряжением
Выясним, как ведет себя каждый элементдействием внешнего переменного напряжения.
под
21.
1. Напряжение на емкости. Емкостное сопротивление.U U 0 cos t
q U 0 C cos t
I q U 0C sin t U 0C cos t
2
Ток опережает напряжение
на емкости на /2.
22.
Амплитуда напряжения на емкости и амплитуда токасвязаны:
U 0 C I 0
Емкостное сопротивление:
U0
1
xC
I 0 C
23. 2. Напряжение на индуктивности. Индуктивное сопротивление
2. Напряжениесопротивление
на
индуктивности.
Индуктивное
U S LI
I I 0 cos t
U L I 0 sin t L I cos t
2
Ток отстает от напряжения
на индуктивности на /2.
24. Индуктивное сопротивление:
U0xL
L
I0
25. Рассмотрим последовательное соединение элементов, на которое подано переменное напряжение.
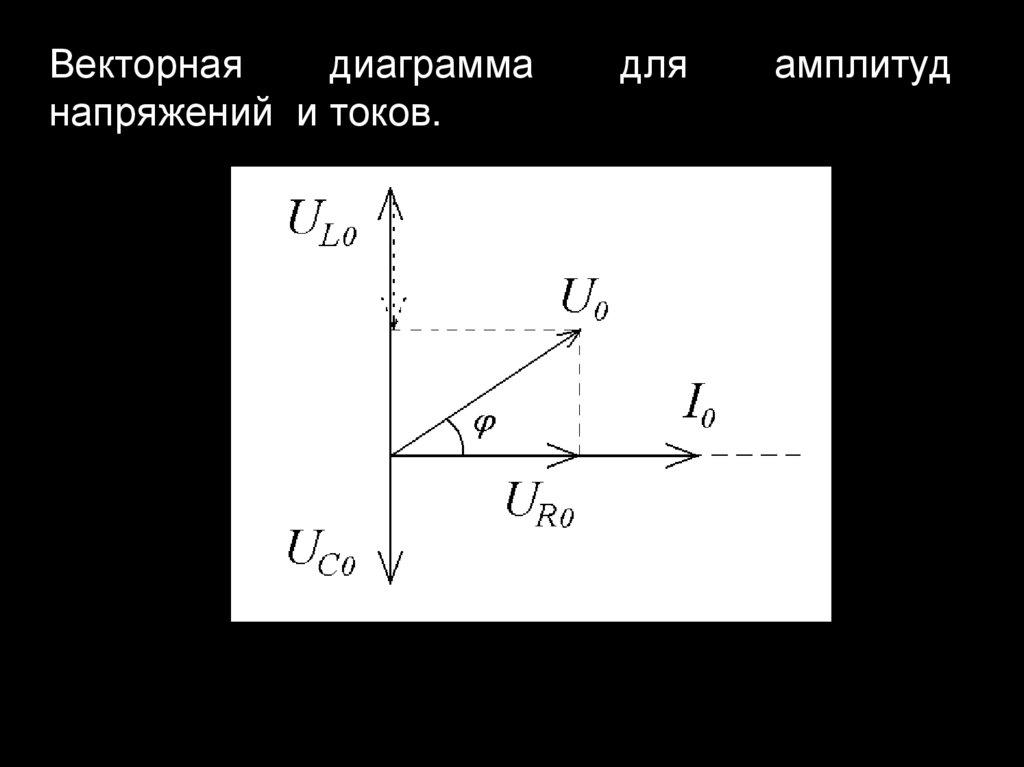
26. Векторная диаграмма для амплитуд напряжений и токов.
Векторнаядиаграмма
напряжений и токов.
для
амплитуд
27. Остается справедливым то, что сумма мгновенных напряжений равна мгновенному внешнему напряжению
U U L U R UC28. Из диаграммы соотношение для амплитуд напряжений и тока:
U02
U R0
RI 0
2
U L 0 U C 0
xL I 0 xC I 0
I 0 R xL xC
2
2
2
2
29. Получили выражение – закон Ома для цепи переменного тока.
Получили выражениепеременного тока.
I0
–
закон
Ома
для
U0
цепи
U0
2
Z
1
2
R L
C
Полное сопротивление цепи (импеданс):
1
Z R L
C
2
2
30. Разность (сдвиг) фаз между напряжением и током:
U L0 U C 0tg
U R0
1
L
C
R
Законы Ома и Кирхгофа остаются справедливыми и для
переменных токов. В этом случае оперируют
комплексными величинами: напряжениями, токами и
сопротивлениями.
31. Мощность, выделяемая в цепи переменного тока
P (t ) U (t ) I (t ) U 0 cos t I 0 cos tU 0 I0
cos cos 2 t
2
32.
U 0 I0U 0 I0
P (t )
cos cos 2 t
cos
2
2
Коэффициент мощности
R
R
cos
2
Z
1
2
R L
C
На практике стремятся сделать так, чтобы
значение коэффициента мощности было
наибольшим (cos →1).
33.
2I0 R
U 0 I0 R
2
P
IЭ R
2 Z
2
Эффективные значения тока и напряжения
I0
IЭ
2
U0
UЭ
2
Эффективным (действующим) значением
тока (напряжения) называется такое значение
постоянного тока, при котором в цепи
выделяется такая же мощность, как и при
прохождении переменного тока.
34.
Мощностьв
цепи
переменного
тока
выражается через эффективные значения
тока, напряжения и коэффициент мощности
(Вт):
P U Э I Э cos
35.
Реактивная мощность в цепи переменного тока (ВАр):Q U Ý I Ý sin
Реактивная мощность в цепи переменного тока,
расходуется
на
поддержание
вызываемых
переменным
током
периодических
изменений
магнитного
поля
и
заряда
конденсаторов.
Характерным отличием Р. м. является то, что
соответствующая ей энергия, не может быть
использована для преобразования в приемниках тока
в полезную работу.
36.
Полная мощность в цепи переменного тока(ВА) :
S Q P
2
2
37. § 37 Резонанс в электрической цепи
38. 1. Амплитуда силы тока может быть выражена через параметры элементов цепи
I0U0
2
1
2
L
R
C
U 0
...
L
I 0 0
L
U 0
0
2
2 2
2 2
4
0
2
0
2 2
4 2 2
39.
2. Амплитудаконденсаторе.
q0
I0
заряда
и
напряжения
U0
L
2
0
2 2
4 2 2
UC0
q0
C
L
U0
0
2
2 2
2 2
4
0
на
40.
2. Амплитудаиндуктивности.
напряжения
U L 0 L I 0
на
катушке
U0
2
2
0
2 2
4
2
U0
0
2
2 2
2 2
0 4
2
2
41. Резонансные частоты:
Для амплитудынапряжения и заряда на
конденсаторе
Для амплитуды тока
Для амплитуды
напряжения на катушке
индуктивности
2
2
0
2
0
0
1 2
0
2
42.
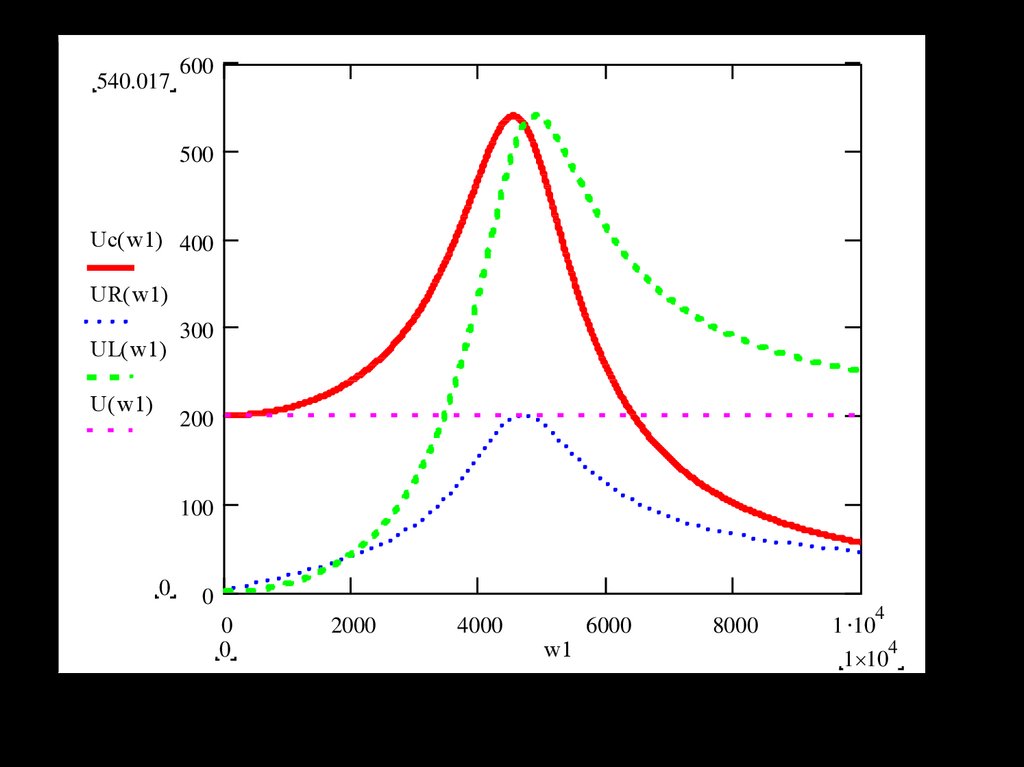
540.017600
500
Uc( w1) 400
UR( w1)
UL( w1)
U ( w1)
300
200
100
0
0
0
0
2000
4000
w1
6000
8000
1 10
4
1 10
4























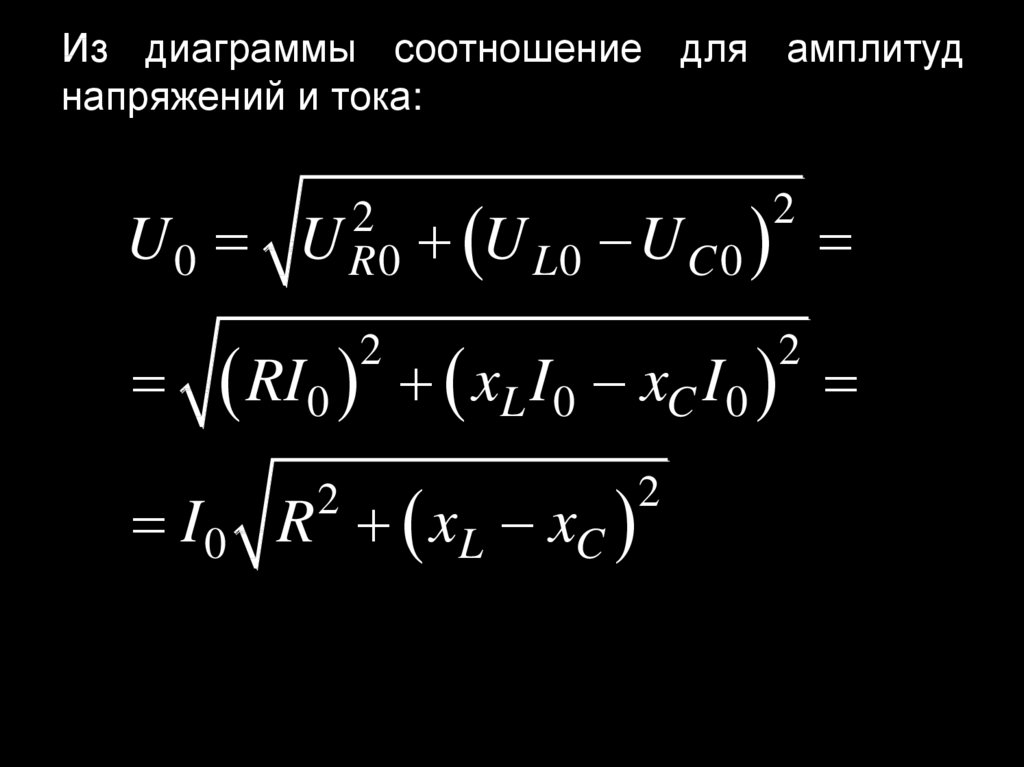













 Физика
Физика








