Похожие презентации:
Теоремы о пределах функции и о непрерывных функциях. Асимптотические приближения. Точки разрыва. (Лекция 4)
1.
Лекция 4. Основные теоремы о пределах функции. Асимптотическиеприближения. Непрерывность функции. Основные теоремы о непрерывных
функциях. Точки разрыва. Классификация точек разрыва.
Основные теоремы о пределах
Предполагается, что функции, рассматриваемые в следующих теоремах
определены на некотором общем множестве Х, для которого точка а является
предельной точкой.
Теорема 1
Если каждое слагаемое алгебраической суммы конечного числа функций имеет
предел при , то предел этой алгебраической суммы при существует и равен такой же
алгебраической сумме пределов слагаемых.
Доказательство
Рассмотрим алгебраическую сумму трех функций f(x)+g(x)-h(x), где
lim x a f ( x) A
lim x a g ( x) B
lim x a h( x) C
Так как функции отличаются от своих пределов на бесконечно малые, то получаем ,
(1), где при f ( x) A ( x); g ( x) B ( x); h( x) C ( x)Из равенств (1), используя теорему об
алгебраической сумме бесконечно малых будем иметь ( x) 0, ( x) 0, ( x) 0
f ( x) g ( x) h( x) ( A B C ) [ ( x) ( x) ( x)] (2), где ( ( x) ( x) ( x)) 0 при x a
2.
Из равенства (2) вытекает, что сумма f(x)+g(x)-h(x) отличается от A+B+C набесконечно малую функцию и следовательно, это число является пределом
данной суммы. Таким образом, имеем
lim x a [ f ( x) g ( x) h( x)] A B C lim x a f ( x) lim x a g ( x) lim x a h( x) (3).
Теорема доказана.
Следствие
Функция может иметь только один предел при x a .
Действительно, если f ( x) A и f ( x) A при x a , то на основании теоремы 1
получим f ( x) f ( x) 0 A A'при x a . Так как предел постоянной функции
равен самой функции и единственен, то имеем A-A’=0, то есть A=A’.
Замечание
В условии теоремы предполагалось, что каждая из функций имеет предел и
доказывалось, что их сумма также имеет предел. Обратное в общем случае
неверно, то есть из существования предела суммы не следует существование
пределов слагаемых.
Пример
2
sin xне существует и lim x cos x не существует
lim x (sin 2 x cos 2 x) 1 ,тогда как lim
x
2
3.
Теорема 2Если каждый из сомножителей конечного числа функций имеет предел при
x a , то предел произведения при x a .
существует и равен произведению пределов сомножителей.
Доказательство
Рассмотрим сначала произведение двух сомножителей f(x)g(x) и пусть lim x a f ( x), A
x a
f ( x) A ( x); g
( x) B ( x);
( x) 0, ( x.)
0
.Имеем
(4),где
,при
Отсюда
lim
g ( x) B
получаем
f ( x) g ( x) (5),где
A B ( x)
( x) A ( x) B ( x(6).
) ( x) ( x)
x a
Из основных теорем о бесконечно малых (теорема 1,2,3) следует, что ( x) 0при x a
.Поэтому на основании равенства (5) будем иметь lim x a [ f ( x) g ( x)] A B lim x a f ( x) lim x a g ( x)
(7).
2)Рассмотрим случай произведения трех функций f(x)g(x)h(x), имеющих
конечные пределы при x a. Используя первую часть доказательства
находим lim [ f ( x) g ( x) h( x)] lim { f ( x)[ g ( x) h( x)]} lim f ( x) lim [ g ( x) h( x)]
x a
x a
x a
lim x a f ( x) lim x a g ( x) lim x a h( x)
Следствие 1
Постоянный множитель можно выносить за знак предела.
Пусть С – постоянная функция,
тогда lim [С g ( x)] lim С lim g ( x) С lim f ( x)
x a
x a
x a
x a
x a
4.
Следствие 2Если функция f(x) имеет предел при x a , то придел x a целой положительной
степени ее равен такой же степени предела этой функции, то есть
lim x a [ f ( x)] n [lim x a f ( x)] n
n N
Пример
2
3
10 20 2 30 3
( x 1)( x 2) 2 ( x 30) 3
10
20
30
lim x
lim x 1 1 1 lim x 1 lim x 1 lim x 1 1 1 1 1
x6
x
x
x
x x x
Лемма
1
Пусть f ( x) A при x a . Тогда обратная по величине функция
f ( x)
в некоторой окрестности U точки а.
a
Доказательство
Положим | A | 0 . На основании определения предела функции имеем
,при
x U a
ограничена
| f ( x) A |
2
. Отсюда получаем | f ( x) | | A [ A f ( x)] | | A | | A f ( x) | | A | | A | | A | 0 при
. Таким образом,
Теорема 3
1
1
2
f ( x) | f ( x) | | A |
x U a
2
.
2
Если функция f(x) имеет предел при x a, отличный от нуля, то предел обратной ей
по величине функции
1
f ( x)
функции, то есть
1
f ( x) lim
lim
x a
равен обратной величине предела данной
1
x a
f ( x)
(8).
| A|
2
5.
ДоказательствоПусть lim x a f ( x) A 0
Тогда на основании леммы и учитывая, что произведение ограниченной функции на
бесконечно малую функции, есть бесконечно малая функция, будем иметь
1
1
1
1
1
1 1
при x a . Отсюда получаем lim
[ A f ( x)] 0
f ( x)
A
x a
A f ( x)
f ( x)
A
lim
x a
f ( x)
Теорема 4
Если делимое f(x) и делитель g(x) имеют пределы при x a и предел делителя отличен
от нуля, то предел их частного при x a равен частному пределов делимого и
делителя, то есть lim f ( x) lim f ( x) (9).
x a
x a
g ( x)
lim x a g ( x)
Доказательство
Пусть lim g ( x) 0 . Тогда, используя теорему о пределе произведения (теорема 2) и
теорему о пределе обратной величины функции (теорема 3), получим
x a
lim x a
lim x a f ( x)
f ( x)
1
1
1
lim x a f ( x)
lim x a f ( x) lim x a
lim x a f ( x)
g ( x)
g ( x)
g ( x)
lim x a g ( x) lim x a g ( x)
Пример
lim
x 1
x2 1
lim
x3 1
x 1
( x 1)( x 1)
lim
( x 1)( x 2 x 1)
x 1
lim x 1 ( x 1)
x 1
2
2
3
x x 1 lim x 1 ( x x 1)
2
6.
Теорема 5Если функция f(x) имеет предел при x a и n f ( x) (n – натуральное) существует в
точке а и в некоторой ее окрестности U a , то lim x a n f ( x) n lim n a f ( x)(10)
Некоторые признаки существования предела функции
Не всякая функция имеет предел, если даже она ограничена. Укажем два признака
существования предела функции.
Теорема о промежуточной функции
Пусть в некоторой окрестности U a точки а функции f(x) заключена между двумя
функциями (x ) и (x) , имеющими одинаковый предел А при x a, то есть
( x) f ( x) ( x) (1) и lim x a ( x) lim x a ( x) A (2), тогда функция f(x) имеет тот же предел,
то есть lim x a f ( x) A (3).
Доказательство
Из неравенства (1) имеем ( x) A f ( x) A ( x) A , отсюда | f ( x) A | max _(| ( x) A |, | ( x) A |)(4).
На основании условия (2) для 0 U a , что | ( x) A | и | ( x) A | при x U a
(5). Поэтому из неравенства (4) получаем | f ( x) A | при x U a . (6)
Определение
1.Функция f(x) называется возрастающей (не убывающей) на данном множестве Х,
x1 x2 ( x , x X )
если из неравенства
следует неравенство f ( x1 ) f ( x2 )
(соответственно f ( x ) f ( x )) .
1
1
2
2
7.
2.Функция f(x) называется убывающей (не возрастающей) на данном множестве Х,если из неравенства x1 x2 ( x1 , x2 X )
следует неравенство f ( x1 ) f ( x2 )
(соответственно f ( x1 ) f ( x2 )) .
3.Возрастающая или убывающая функция называется монотонной на данном
множестве Х.
Теорема
Пусть функция f(x) монотонна и ограничена при x<a и x>a. Тогда существует
соответственно левый предел lim x a 0 f ( x) f (a 0)
и правый предел ее lim x a 0 f ( x) f (a 0) .
Если lim x a 0 f ( x) f (a 0) = lim x a 0 f ( x) f (a 0) , то функция имеет предел в точке а.
8.
Первый замечательный предел(предел отношения синуса бесконечно малой дуги к самой дуге)
Теорема Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в
радианах, равен единице, то есть
sin x
lim x 0
1
(1)
x
Доказательство
B
C
O
A
Рассмотрим в координатной плоскости круг радиуса R с центром в начале координат
OA R, AOB x,0 x
2
, AC OA
S AOB S сект.AOB S AOC
то есть
x
sin x
1 2
1
1
R sin x R 2 x R 2 tgx
2
2
2
1
cos x
1
или
x
1
sin x cos x
.
В силу четности функций
и
это неравенство справедливо и для
интервала x 0 . Перейдя в этом неравенстве к пределу при x 0 и заметив,
2
что в силу непрерывности функции cosx при х=0 имеет место равенство lim x 0 cos x 1
sin x
x
получим lim
что равносильно lim
.
1
1
x 0
sin x
x 0
x
9.
Второй замечательный пределРассмотрим выражение 1 1n , где n – натуральное число.
Задаем для n неограниченно возрастающие значения и вычисляем
Получим следующий результат
n
n
1
1
n
n
1
2
10
100
1000
10000
2
2,25
2,594
2,705
2,717
2,718
1
1
n
1
1
n
n
.
n
Как видно из таблицы при увеличении n выражение
изменяется все
медленнее и стремится к некоторому пределу, приближенно равному 2,718.
Теорема
n
1
Последовательность 1 стремится к конечному пределу, заключенному между 2
n
и 3.
(Доказательство на основании разложения по биному Ньютона). Этот предел
называется числом e. Итак e lim n 1 1 n ,е=2,7182818284…
Рассмотрим функцию
1
1
x
x
n
,где ( x ( , 1) (0, )) Можно доказать, что e lim x
Другое выражение для числа е. Полагая
1
( 1)
x
1
1
x
будем иметь e lim 0 1 .
1
x
10.
При вычислении пределом полезно применять следующие формулы:1
ln( 1 x)
k x
k
;
lim x 0 (1 kx) x e k ; lim x 0
1 . Данные формулы легко получаются из
lim x (1 ) e
x
x
двух основных формул.
Понятие об асимптотических формулах
Пусть ( x ), ( x ) -функции определенные в окрестности точки а. Обобщая
определение о бесконечно малой функции будем говорить, что ( x) 0( ( x))при x a (1).
если ( x) ( x) ( x) где ( x ) 0 при x a (2).
( x)
0 (3).
Если ( x ) 0 в некоторой окрестности точки а, то из (2) имеем lim x a
( x)
Определение
Если при x aсправедливо равенство f ( x ) ( x ) 0( ( x ))
асимптотическим выражением для функции f(x) при
Используется запись f ( x ) ~ ( x ) при x a .Если
f ( x)
получаем lim
(5).
1
x a
( x) 0
x)
(4), то функция (называется
.
, то при
x a
x U a
из формулы (4)
( x)
Выясним условие существования для функции f(x) ненулевого асимптотического
приближения ( x ) kx b при x (6).
11.
Пусть f ( x ) kx b ( x ) (7) где ( x ) 0 при x , то есть( x ) 0( x )
,причем очевидно также, что ( x ) 0( kx b) при x .Их (7) будем иметь
при x
f ( x)
b ( x)
k
x
x
x (8)
Переходя к пределу при x в равенстве (8) и учитывая, что ( x ) 0при x
x
получим k lim x f ( x ) (9).Из формулы (7) b lim x [ f ( x) kx] (10).
x
Обратно, если существуют пределы (9),(10), из которых хотя бы один не нулевой, то
справедливо асимптотическое разложение (7).
График линейного асимптотического разложения y=kx+b называется асимптотой кривой
y=f(x) и имеет вид:
Y=kx+b M’
“”””
”’
M
y=f(x)
Здесь для точек M(x,y) и M’(x,Y) Y y MM ' 0 при x
12.
ПримерПостроить при x линейную асимптотическую формулу для функции
f ( x) x 2 x 1
Решение
Используя формулы (9),(10) имеем
b lim x ( x 2 x 1 x ) lim x
x 1
x2 x 1 x
k lim x
lim x
x2 x 1
1 1
lim x 1 2 1
x
x x
1
1
x
2
1 1
1 2 1
x x
1
1
Таким образом f ( x) x 2 x 1 ~ x 2 при x .
Непрерывность функции
Приращение аргумента и функции.
Пусть х– некоторое значение данной переменной величины. Наряду с х рассмотрим
и другое значение этой переменной величины .
Определение 1
Приращением некоторой переменной величины называется разность между новым
значением этой величины и ее прежним значением. В нашем случае
( x1 x)
13.
Обозначение x x1 x - приращение величины х.Прибавляя к значению переменной величины ее приращение, получаем приращенное
значение этой величины.
x x -приращенное значение величины х.
Рассмотрим функцию y=f(x) (1)
Даём x для х, тогда y получает соответствующее приращение y . Очевидно это
можно записать y y f ( x x )(2). Из (1) и (2) следует y f ( x x ) f ( x ) (3).
Геометрическая интерпретация
M
M’
‘”‘’
‘
Y=f(x)
B
C
A
x
N
N’
}“’
Кривая АВ – график функции f(x).
14.
Рассмотрим точку M(x,y). Даем приращение координате х - x .Тогда ордината yполучит приращение y . Точка M(x,y) займет положение
M ( x x, y y )
.
Пусть С – точка пересечения прямой параллельной ОХ и перпендикуляра M’N’ на ОХ.
Очевидно MC x, CM ' y .
Может случиться, что для некоторого х при стремлении x 0 точка M’
неограниченно приблизится к М, то есть
y 0
.
В таком случае y=f(x) называется непрерывной при данном значении х.
Определение 2
Функция называется непрерывной в данной точке, если в этой точке бесконечно
малому приращению аргумента соответствует бесконечно малое приращение
функции.
Используя понятие предела функции, получаем развернутое определение
непрерывности функции в точке.
Определение 3
Функция f(x) непрерывна в точке тогда и только тогда, когда 0, ( , x1,) такое, что
(4),если
x x1 x1 0 приращение.
| x1 | x1
| f ( x) f ( x1 ) | fи( x1 x1 ) f ( x,1 ) | любое допустимое
15.
Определение 4Функция f(x) называется непрерывной на данном множестве Х, если
1)она определена на этом множестве, то есть x X f ( x )
2) непрерывна в каждой точке этого множества, то есть
x X справедливо
равенство
lim x 0 y lim x 0 [ f ( x x ) f ( x )] 0 (5), где x x X.
Пример
Исследовать на непрерывность функцию
y x2
Решение
Давая х приращение x , получим y ( x x) 2 x 2 x(2 x x)
Очевидно, каково бы ни было фиксированное значение х, если
есть функция непрерывна при любом x R.
x 0,то y 0
,то
Определение 5
Точка, в которой нарушается непрерывность функции называется точкой разрыва этой
функции. Если x x0 -точка разрыва функции y=f(x), то возможны два случая:
1) функция f(x) определена при x x0 ,причём
y f ( x0 x0 ) f ( x0 ) 0при x0 x x0 0
16.
2) функция f(x) не определена при x x0 и говорить о приращении функции в точкеx x0 не имеет смысла . В этом случае условимся x x0 называть точкой разрыва
функции f(x) только тогда, когда функция f(x) определена в непосредственной
близости значения x 0 .
Если можно изменить или дополнительно определить функцию f(x) в точке
x x0
,то есть выбрать число f ( x0 ) , так, что измененная или дополненная функция f(x)
будет непрерывна при x x0,то эта точка называется устранимой точкой разрыва
функции f(x).
В противном случае, то есть когда функция f(x) остается разрывной при x x0при
любом выборе числа значение называется неустранимой точкой разрыва функции
f(x).
Пример 1
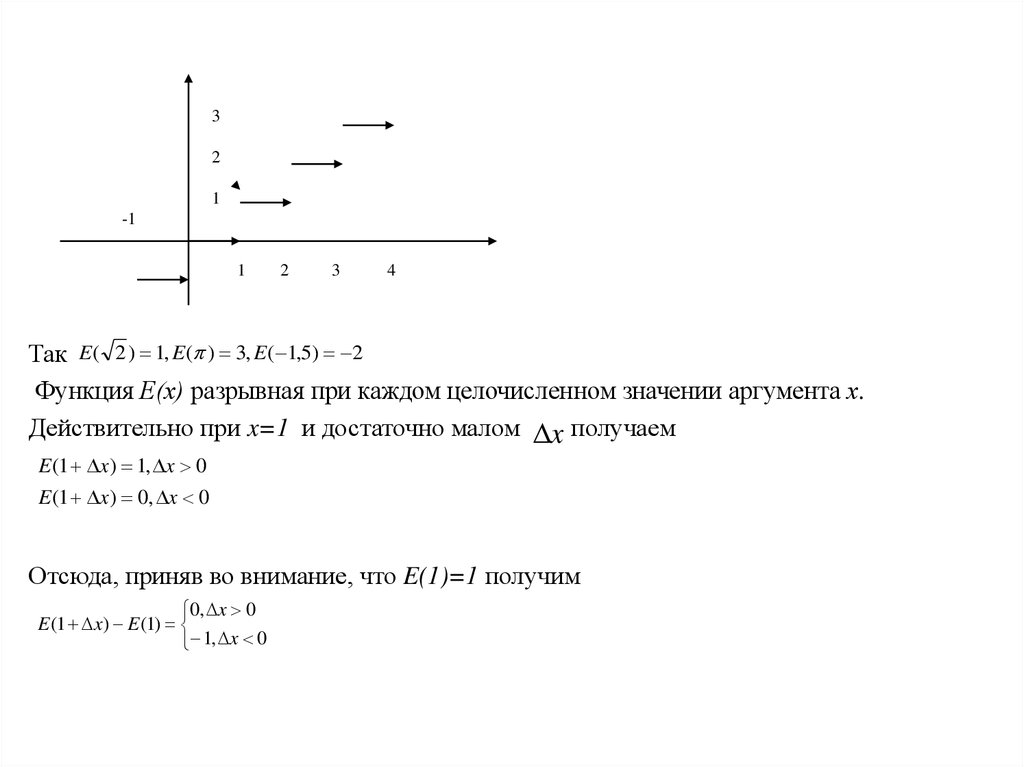
Рассмотрим функцию Е(х), равную целой части числа х, то есть, если x=n+q, где n –
целое число, 0 q 1, то E(x)=n
17.
32
1
-1
1
2
3
4
Так E ( 2 ) 1, E ( ) 3, E ( 1,5) 2
Функция Е(х) разрывная при каждом целочисленном значении аргумента х.
Действительно при x=1 и достаточно малом x получаем
E (1 x ) 1, x 0
E (1 x ) 0, x 0
Отсюда, приняв во внимание, что E(1)=1 получим
0, x 0
E (1 x ) E (1)
1, x 0
18.
Следовательно, приращение функции y E(1 x ) E(1) не стремится к нулю при x 0то есть функция разрывная при х=1. Аналогичное рассуждение можно провести и для
x=k, где k -целое.
Пример 2
Функция f ( x ) 1 , не определена при х=2, но имеет смысл для всех значений x 2
( x 2) 2
2
Какое бы значение не приписывали числу f(2), всегда будем иметь
f (2 x ) f (2)
1
f ( 2)
( x ) 2
при
x 0
. Таким образом, при х=2 при любом выборе
значения f(2) при x 0 y , следовательно, эта функция имеет
неустранимую точку разрыва при х=2.
19.
В виду важности понятия непрерывности функции приведем другое определениенепрерывности функции в точке, эквивалентное, приведенному выше.
Определение 6
Функция f(x) называется непрерывной при , если
эта функция определена при ;
имеет место равенство lim
(1).
x x f ( x ) f ( x1 )
То есть функция непрерывна в данной точке , тогда и только тогда, когда предел
1
функции при x x1
равен значению функции в предельной точке. Точка предельная точка области определения функции f(x).
Для функции, непрерывной на множестве Х, в силу формулы (1) для каждого значения
x1 X выполнено неравенство x x1
Так как x1 lim x x x ,то отсюда получаем lim x x f ( x ) f (lim x x x )(2) , то есть , если функция
непрерывна, то знаки предела и функции перестановочны.
Справедливо усиленное свойство перестановочности функции f(x) и предела, а именно
x (t ) - непрерывная функция (t ) x1 при t t1 , тогда для f(x) имеем
1
lim t t1 f ( (t )) f (lim t t1 (t ))
1
1
20.
Основные теоремы о непрерывных функцияхТеорема 1
Сумма конечного числа непрерывных функций есть функция непрерывная.
Доказательство
Пусть f1 ( x), f 2 ( x-) непрерывные функции на множестве Х и x1 X , тогда
lim x x [ f 1 ( x ) f 2 ( x )] lim x x f 1 ( x ) lim x x f 2 ( x ) f 1 ( x1 ) f 2 ( x2 ) , то есть предел суммы
1
x x1
1
1
при
равен значению этой суммы при x x1 . Следовательно f1 ( x) f 2 ( x) также
непрерывная на множестве Х.
Теорема 2
Произведение конечного числа непрерывных функций есть функция непрерывная.
Доказательство аналогично доказательству в теореме 1.
Следствие
Полином P( x ) a0 a1 x ... an x n - непрерывная функция.
Теорема 3
Частное от деления двух непрерывных функций есть функция непрерывная во всех
точках, в которых делитель отличен от 0.
Доказательство аналогичное.
21.
Следствиеa0 a1 x ... an x n
Дробно-рациональная функция R( x ) b0 b1 ... bm x m
непрерывна всюду за
исключением тех значений х, где знаменатель обращается в 0.
Теорема 4
Непрерывная функция от непрерывной функции также непрерывна. Сложная функция, состоящая
из непрерывных функций, непрерывна.
Доказательство
Пусть x1 X и
f ( ( x ))
- определена в этой точке, причем u ( x )непрерывная в точке
x x1 , а f(u) непрерывная в точке u1 ( x1 ) . На основании усиленного свойства
перестановочности функции и предела имеем lim x x f ( ( x )) f (lim x x ( x )) f ( ( x1 )) , то
1
1
есть f ( ( x )) непрерывная в точке x x1 .
Пример
Функции (sin x ) 2 и sin( x) 2 - непрерывные в силу непрерывности функций sinx и x 2
Теорема 5
Если функция y=f(x) непрерывная и строго монотонная на интервале (a,b), то
существует однозначная обратная функция , определенная на интервале (f(a),f(b)),
которая также непрерывная и монотонная.
22.
Раскрытие неопределенностейМожет случиться, что f(x) определена и непрерывная всюду, за исключением
некоторого значения x x1 , при котором функция f(x) теряет смысл, то есть
становиться неопределенной. Каким образом можно выбрать число . Чтобы
дополненная функция была непрерывной при x x1 . Для этого необходимо и
достаточно выполнение равенства lim x x f ( x ) f ( x1 ) . Операция нахождения
предела функции f(x) при x x1 в этом случае называется раскрытием
неопределенности, а сам предел, если он существует носит название истинного
значения функции f(x) при x x1
Пример
x2 4
при х=2 функция не определена. Полагая, дополнительно
f ( x)
1
x 2
f (2) lim x 2
x2 4
lim x 2 ( x 4) 4
x 2
получим функцию непрерывную всюду, в том числе и
при х=2. Если же положить
f ( 2) 4 ,то то соответствующая функция будет
разрывная при х=2.
4
2
23.
Классификация точек разрываОпределение
Точка x 0 разрыва функции f(x) называется точкой разрыва первого рода, если
существуют конечные односторонние пределы функции
lim
lim
x x0 0
x x0 0
f ( x ) f ( x0 0)
f ( x ) f ( x0 0)
При этом f(x) не обязательно должна быть определена в точке x 0 , то есть f ( x0 )
может не существовать
B=f(a+0)
A=f(a-0)
a
- называется скачком функции f(x) в точке x 0
Все прочие точки разрыва x1 функции f(x) называются ее точками разрыва второго
рода.
f ( x0 0) f ( x0 0)
Точки бесконечного разрыва x1 характеризуются тем, что для них существуют
односторонние пределы
24.
limx x1 0
f ( x ) f ( x1 0)
lim
x x1 0
f ( x ) f ( x1 0)
хотя бы один из которых, является бесконечным.
В этом случае прямая x x1 называется вертикальной асимптотой графика функции
f(x)























 Математика
Математика








