Решение квадратного уравнения

1. РЕШЕНИЕ КВАДРАТНОГО УРАВНЕНИЯ

НАЧАТЬ

2.

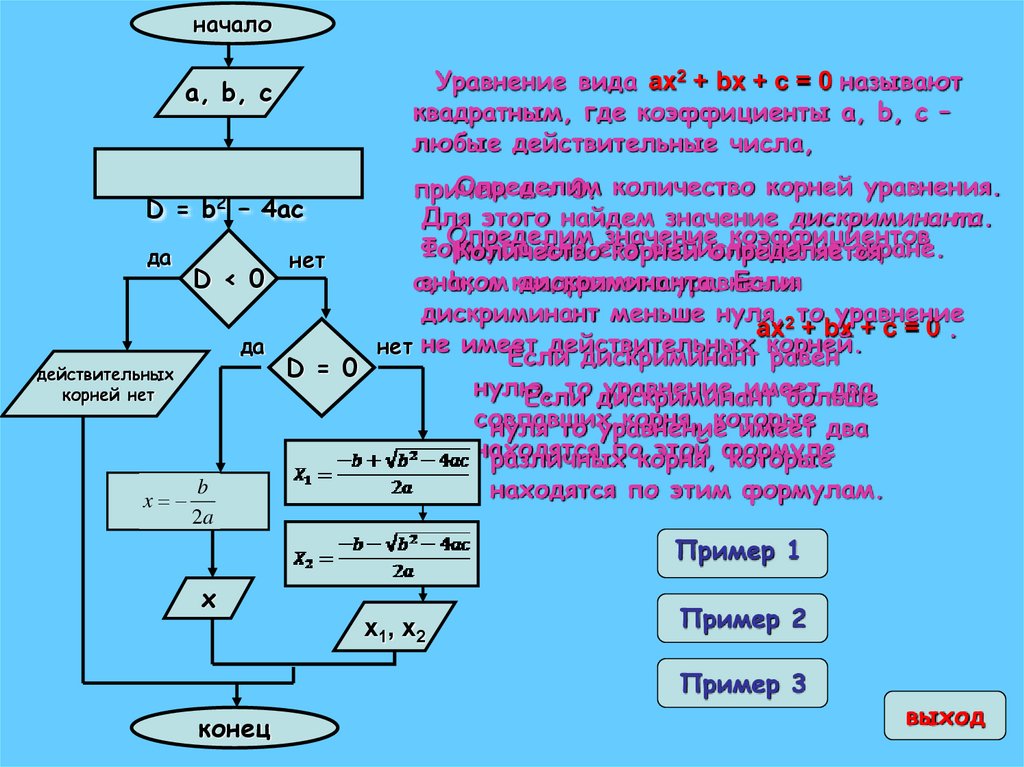
начало
Уравнение вида ax2 + bx + c = 0 называют
квадратным, где коэффициенты a, b, c –
любые действительные числа,
a, b, c
D =
да
b2
– 4ac
D < 0
да
действительных
корней нет
x
нет
D = 0
Определим
причем
a ≠ 0. количество корней уравнения.
Для этого найдем значение дискриминант а.
Определим
значение
коэффициентов
Формула
для его
вычисления
на экране.
Количество
корней
определяется
a,
b, с квадратного
уравнения
знаком
дискриминанта.
Если
дискриминант меньше нуля,2 то уравнение
ax + bx + c = 0 .
действительных
нет не имеет
Если дискриминант корней.
равен
нулю,
то дискриминант
уравнение имеет
два
Если
больше
совпавших
корня, которые
нуля то уравнение
имеет два
находятся
покорня,
этой формуле
различных
которые
находятся по этим формулам.
b
2a
Пример 1
x
x1, x2
Пример 2
Пример 3
конец
выход

3. Пример 1

начало
Пример 1
a, b, c
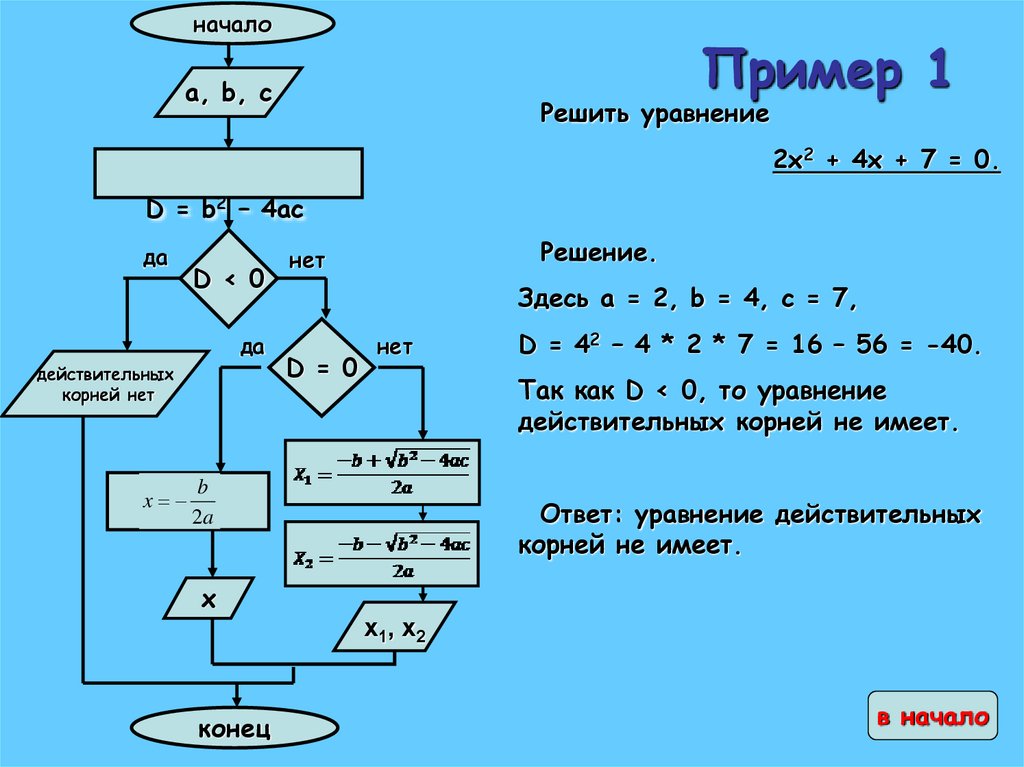
Решить уравнение
2x2 + 4x + 7 = 0.
D = b2 – 4ac
да
D < 0
да
действительных
корней нет
x
Решение.
нет
Здесь a = 2, b = 4, c = 7,
D = 0
нет
D = 42 – 4 * 2 * 7 = 16 – 56 = -40.
Так как D < 0, то уравнение
действительных корней не имеет.
b
2a
Ответ: уравнение действительных
корней не имеет.
x
x1, x2
конец
в начало

4. Пример 2

начало
Пример 2
a, b, c
Решить уравнение
4x2 - 20x + 25 = 0.
D = b2 – 4ac
да
D < 0
да
действительных
корней нет
Решение.
нет
Здесь a = 4, b = -20, c = 25,
D = 0
нет
D = (-20)2 – 4 * 4 * 25 = 400 – 400 = 0.
Так как D = 0, то уравнение имеет два
совпавших корня.
20
Значит, x1 = x2 =
= 2,5.
2*4
x1 = x 2 =
= - b / (2a)
Ответ: корень уравнения: x = 2,5.
x
x1, x2
конец
вв начало
начало

5. Пример 3

начало
Решить уравнение
a, b, c
Пример 3
3x2 + 8x - 11 = 0
D =
да
b2
Решение.
– 4ac
D < 0
да
действительных
корней нет
Здесь a = 3, b = 8, c = -11,
нет
D = 0
D = 82 – 4 * 3 * (-11) = 64 + 132 = 196.
нет
Так как D > 0, то уравнение имеет два
различных корня.
Значит,
x
b
2a
x1 = (- b +
D ) / (2a)
x2 = (- b -
D ) / (2a)
6
=
6
=
= 1
11
3
Ответ: корни уравнения: x1 = 1,
x
x1, x2
конец
8 196
x1 =
2*3
8 196
x2 =
2*3
11
x2 =
3
в начало