Вывод формулы Резерфорда для вероятности обратного рассеяния альфа-частиц. АФ1.A

1.

1.10. Вывод формулы Резерфорда для вероятности
обратного рассеяния альфа-частиц
В качестве упражнения, выведем формулу Резерфорда.
2
Ze d
dN Nnh
2
Mv sin 4
2
2
dN – число частиц, рассеянных в телесный угол d ;
N – число падающих частиц;
– угол рассеяния;
M и v – (приведенная) масса и скорость -частицы;
Z и n – заряд и концентрация атомов в рассеивающей фольге;
h – ее толщина.
1

2.

Рассмотрим задачу двух тел, взаимодействующих посредством кулоновской
силы, квадратично спадающей с расстоянием.
Это – основное содержание гипотезы Резерфорда, подтвержденной по
итогам сопоставления результатов последующих расчетов с полученными
им экспериментальными данными.
Математически постановка задачи сходна с задачей небесной механики,
только знак взаимодействия противоположный.
Решение для траектории – кривая второго порядка. Гипербола.
2

3.

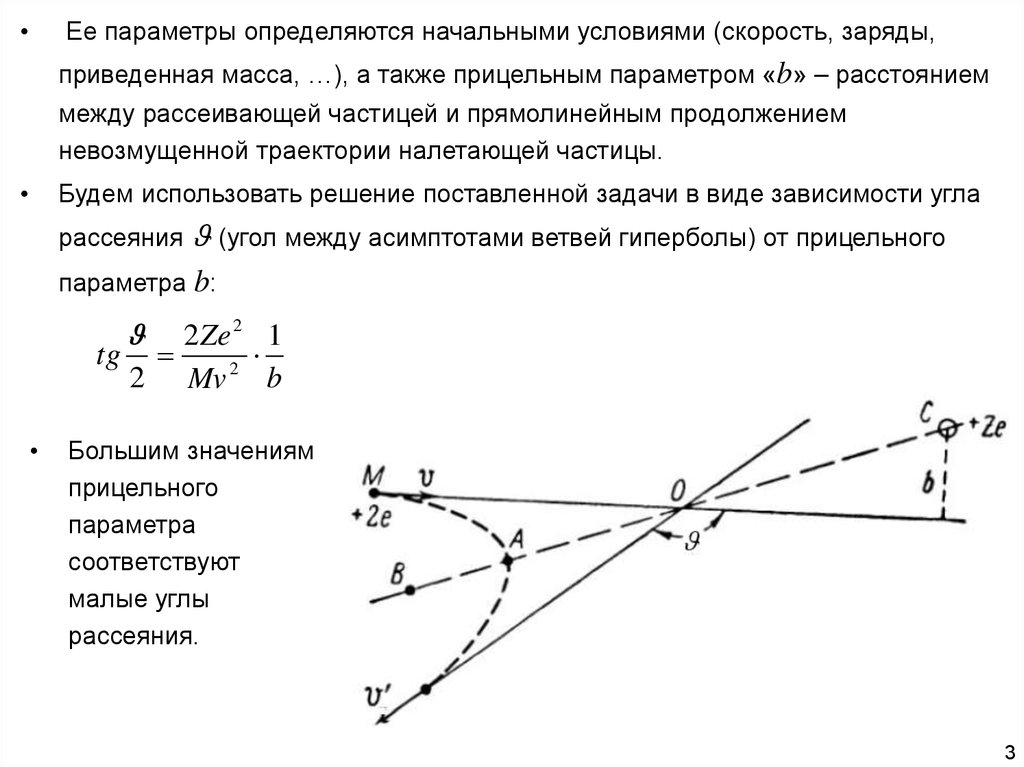
Ее параметры определяются начальными условиями (скорость, заряды,
приведенная масса, …), а также прицельным параметром «b» – расстоянием
между рассеивающей частицей и прямолинейным продолжением
невозмущенной траектории налетающей частицы.
Будем использовать решение поставленной задачи в виде зависимости угла
рассеяния (угол между асимптотами ветвей гиперболы) от прицельного
параметра b:
2Ze 2 1
tg
2
2 Mv b
Большим значениям
прицельного
параметра
соответствуют
малые углы
рассеяния.
3

4.

Вычислим вероятность того, что прицельный параметр пробной -частицы,
случайно «запущенной» в пределах участка мишени площадью S, по
отношению к одной конкретной рассеивающей частице будет принадлежать
интервалу [b; b+db].
2 b db
S
Из рисунка, эта вероятность равна отношению площадей:
Умножив полученное значение на число рассеивающих частиц в
рассматриваемой части мишени, получим вероятность
dw того, что
прицельный параметр пробной частицы окажется в интервале [b; b+db] по
отношению к одной из частиц мишени.
dw
2 b db
nhS 2 nhb db
S
В этом случае, угол рассеяния будет
близок к , удовлетворяющему условию
2Ze 2 1
tg
2
2 Mv b
4

5.

В этом случае, угол рассеяния будет близок
к , удовлетворяющему условию:
2Ze 2 1
tg
2
2 Mv b
«Близок» – значит в пределах [ ; +d ]
В пространстве этому условию
соответствует телесный угол
d :
d 2 sin d
Чтобы избавиться от неизмеримого в эксперимента прицельного параметра
в ранее полученной формуле
dw 2 nhb db
и перейти к измеримой вероятности рассеяния в от телесный угол, поделим
два последних выражения друг на друга:
dw
b
db
nh
d
sin d
5

6.

dw
b
db
nh
d
sin d
Сюда можно подставить зависимость b от угла рассеяния
2Ze 2 1
tg
2
2 Mv b
2 Ze 2 1
b
2
Mv tg
2
Отсюда же вычислим и нужную нам производную (она отрицательна, но нам
это неважно):
db 2Ze 2
1
1
d
Mv 2 tg 2 2 cos 2
2
2
Подставив b и db/d в верхнюю формулу, получим для вероятности
рассеяния в телесный угол:
2Ze 2
dw
nh
2
d
Mv
2
1
1
tg sin 2tg 2 cos 2
2
2
2
6

7.

для вероятности рассеяния в телесный угол:
2Ze 2
dw
nh
2
d
Mv
2
1
1
tg sin 2tg 2 cos 2
2
2
2
sin 2 sin
Использовав тригонометрическое тождество
2
получим
Ze 2
dw
nh
2
d
Mv
1
sin
4
2
cos
2
,
.
2
Вероятность dw связывает число падающих -частиц N с числом dN
частиц, рассеянных в телесный угол
d вблизи угла рассеяния :
dN N dw
2
Ze
d
dN Nnh
2
Mv
sin 4
2
Окончательно:
Это и есть формула Резерфорда.
2
7