Квадратное уравнение и его корни

1. Квадратное уравнение и его корни

1 урок

2. Устно:

Является ли число 7,5 корнем уравнения 2 х 7 8?
Найдите корни уравнения (6 х 5)( х 5) 0
х 1 3
Площадь квадрата равна 36 кв.м. Найдите длину
стороны квадрата.
Мальчик задумал число, возвел его в квадрат и
получил 144. Он попросил товарищей отгадать
задуманное число. Они дали ему два различных ответа
и оба оказались правы. Разве это возможно?
х 2 25
Разложите на множители :
16
х
81
х2 7
2

3. Внимательно рассмотрите предложенные равенства и условно разбейте их на 4 группы:

2
3
)
9
x
4
2)3 4 7
1) x 4
4)3 x 6 x 8 0
2
5)5 x 7 2
7) 0,5х 8 6 х 8)1 9 х 7 х
2
3 2
2
7
7
10)
9
21
6)4 х 4 81
3х 2 7 4 х
9)
1
2
7
9 х 3х 4
11)
0
2
12
12)3х3 3

4. Внимательно рассмотрите предложенные равенства и условно разбейте их на группы:

2)3 4 7
3 2
2
7
7
10)
9
21
3)9 x 2 4
2
4)3 x 6 x 8 0
7) 0,5х 2 8 6 х
2
3х 7 4 х
9)
1
2
7
1) x 4
5)5 x 7 2
9 х 3х 4
11)
0
2
12
6)4 х 4 81
8)1 9 х 7 х
12)3х 3
3

5. Квадратное уравнение —уравнение вида ax² + bx + c = 0, где a, b, c — некоторые числа (a ≠ 0) x — неизвестное

4)3х 6 х 8 0
3)9 х 4
2
2
7) 0,5х 8 6 х
2
3х 7 4 х
9)
1
2
7
2

6. Квадратное уравнение —уравнение вида ax² + bx + c = 0, где a, b, c — некоторые числа (a ≠ 0) x — неизвестное.

3х 6 х 8 0
2
9х2 4
2
9х 4 0
3х 6 х ( 8) 0
2
9 х 2 0 х ( 4) 0
0,5х 2 8 6 х
0,5х 6 х 8 0
2
3х 7 4 х
1
2
7
2
21х 8 х 35 0
2

7. Квадратное уравнение —уравнение вида ax² + bx + c = 0, где a, b, c — некоторые числа (a ≠ 0) x — неизвестное.

...х ...х ... 0
2
a = -0,003
b=0
c=0
a=5
b = -1,5
c=0
a= 7
b=0
c =4
3
11
a=
b = 3 5
c = -6

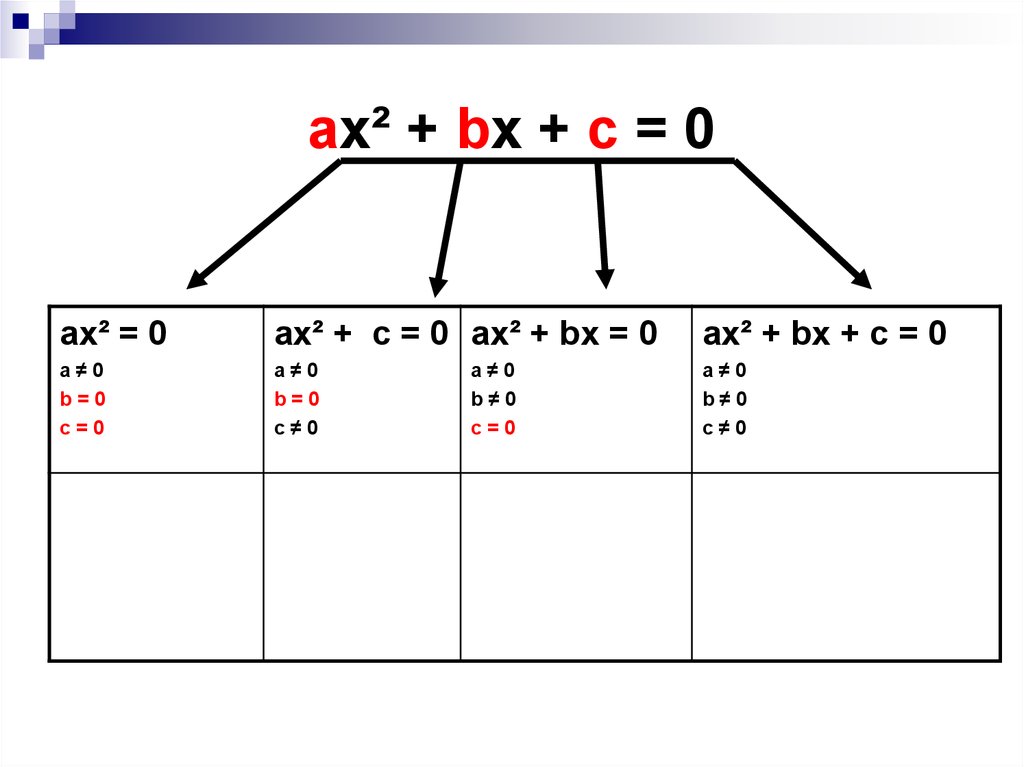
8. ax² + bx + c = 0

ax² = 0
ax² + c = 0 ax² + bx = 0
ax² + bx + c = 0
a≠0
b=0
c=0
a≠0
b=0
c≠0
a≠0
b≠0
c≠0
a≠0
b≠0
c=0

9. ax² + bx + c = 0

ax² = 0
ax² + c = 0 ax² + bx = 0
ax² + bx + c = 0
a≠0
b=0
c=0
a≠0
b=0
c≠0
a≠0
b≠0
c≠0
a≠0
b≠0
c=0

10. Квадратное уравнение —уравнение вида ax² + bx + c = 0, где a, b, c — некоторые числа (a ≠ 0) x — неизвестное

Квадратное уравнение может иметь два
корня, один корень (одинаковые) или не
иметь корней;
Если сумма коэффициентов равна нулю, то
квадратное уравнение имеет два различных
корня;
Если сумма коэффициентов a и c равна b,
то уравнение имеет два различных корня;

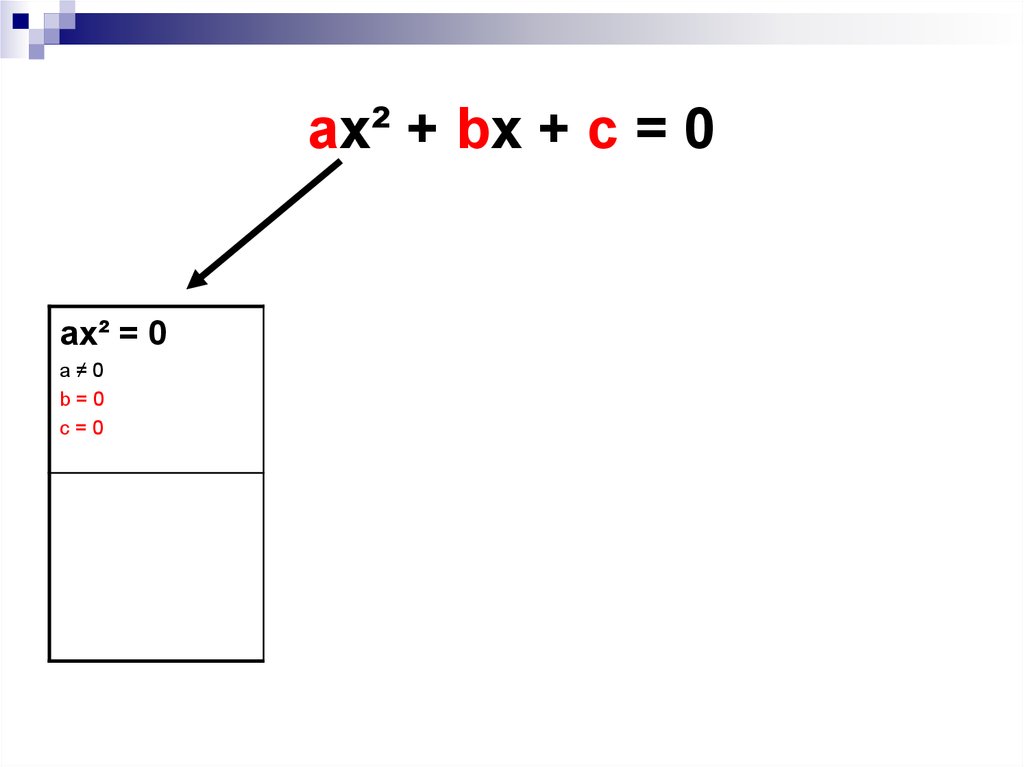
11. ax² + bx + c = 0

ax² = 0
a≠0
b=0
c=0

12. ax² + bx + c = 0

ax² = 0
ax² + c = 0
a≠0
b=0
c=0
a≠0
b=0
c≠0

13. Уравнение вида имеет два корня и

Уравнение вида
имеет два корня
х d, где d 0
2
d и d
Если d = 0, то уравнение имеет один
корень х = 0.
Если d < 0, то уравнение не
имеет действительных корней.

14. Подведем итоги:

Уравнение вида…………..
называется ………;
Числа a, b, c называются
соответственно…………………………………;
По значению коэффициентов делятся
на ………………… и
………………..уравнения;
Может иметь…………. корней;
Уравнения вида
х2 d, где d 0
имеют корни…………

15. Квадратное уравнение и его корни

2 урок

16. ax² + bx + c = 0

ax² = 0
ax² + c = 0
a≠0
b=0
c=0
a≠0
b=0
c≠0

17. ax² + bx + c = 0

ax² = 0
ax² + c = 0 ax² + bx = 0
a≠0
b=0
c=0
a≠0
b=0
c≠0
a≠0
b≠0
c=0

18. Квадратное уравнение —уравнение вида ax² + bx + c = 0, где a, b, c — некоторые числа (a ≠ 0) x — неизвестное

Если в квадратном уравнении
коэффициенты b и с не равны нулю, то
уравнение называется полным
квадратным уравнением;
Если один из коэффициентов b или с
равен нулю, или оба коэффициента
равны нулю, то квадратное уравнение
называется неполным.

19. До свидания!