Модуль «Алгебра». ГИА 2013

1. ГИА 2013 Модуль «АЛГЕБРА»

2. Модуль «Алгебра»

Решите неравенство 7+2(х-4)≥х+4.
7 2(x - 4) x 4
7 2x - 8 x 4
2x - x 7 - 4 0
x -3
x
-3
2
Ответ: [-3;+∞)

3. Повторение

При решении неравенства можно переносить
слагаемые из одной части в другую, меняя
знак слагаемых на противоположный.
Уравнение вида aх+b≥0 называется
линейным.
Числа, которые больше данного числа, на
числовой прямой лежат правее данного
числа.
Если неравенство содержит нестрогий
знак (≥), то соответствующая точка на
числовой прямой будет темной, а
скобка в ответе квадратной.
3

4. Модуль «Алгебра»

2 x
4 .
Решите неравенство
x 3
2 x
4
x 3
1)
2 x 4( x 3)
2 x 4x 12
x 4x 12 2
5x 14 : ( 5)
x 2,8
2) Так как неравенство
содержит рациональную
дробь, то ее знаменатель не
может быть равен нулю.
x 3 0
x 3
2,8
Ответ: [-2,8; 3), (3;+∞).
4
3
x

5. Повторение

Если обе части неравенства разделить на
одно и то же отрицательное число, то
необходимо изменить знак неравенства на
противоположный.
Если в промежуток входит светлая точка, то
этот промежуток разбивается на две части, а
в ответ записывается круглая скобка,
соответствующая светлой точке.
5

6. Модуль «Алгебра»

Решите систему неравенств
4 4 x 1
1) .
5 x 3 2
4 x 1 4
4 4 x 1
5x 3 2.
1
5
2) .
5
4
5 x 2 3
6
4 x 5
: ( 4)
5x 1
:5
5
x
4
1
x
5
3) .
4) .
1
5
5
4
x
5
4
3
4
1
3
4
Ответ: 2.
x
x
x
x

7. Повторение

Данная система представляет собой систему
линейных неравенств, в которой решаются
одновременно оба неравенства.
Если числитель дроби меньше знаменателя,
то дробь правильная, если же числитель
больше знаменателя, то дробь неправильная.
Неправильная дробь больше правильной, и
соответственно правее на числовой прямой.
Решением системы неравенств
является тот промежуток, где
штриховки совпадают.
7

8. Модуль «Алгебра»

1)(-∞;-8),(4;+∞)
2)(-∞;-4),(3;+∞)
õ2 4 õ 12 5 õ ⇒ õ2 õ 12 0
3)(-∞;-3),(4;+∞)
Рассмотрим соответствующую функцию у=х²-х-12. 4)(4;+∞)
Её график – парабола, ветви направлены вверх (а>0).
Найдем нули функции (абциссы точек пересечения графика с осью Ох).
Решите неравенство х²+4х-12>5х.
õ2 õ 12 0
⇒
x1 4;
x2 3
Изобразим геометрическую модель решения неравенства.
Т.к. неравенство содержит знак «больше 0»,
то на рисунке надо взять промежуток,
x где часть графика выше оси Ох.
4
3
Ответ: 2.
8

9. Повторение

Неравенство вида ах²+bx+с>0 называется
квадратным (неравенством второй степени
с одной переменной)
Приведенным называется квадратное
уравнение, старший коэффициент которого
равен единице.
Если числа х₁ и х₂ таковы, что х₁+х₂=-b,
х₁∙х₂=с, то эти числа – корни уравнения
(обратная теорема Виета).
9

10. Модуль «Алгебра»

Решите неравенство -2х²-5х≥-3.
- 2x 2 - 5x -3 ⇒ - 2x 2 - 5x 3 0
Рассмотрим соответствующую функцию у = -2х²-5х+3.
Её график – парабола, ветви направлены вниз (а<0).
Найдем нули функции (абциссы точек пересечения графика с осью Ох).
- 2x 2 - 5x 3 0
x1 0,5;
x2 3
Изобразим геометрическую модель решения неравенства.
Т.к. неравенство содержит знак «больше 0»,
то на рисунке надо взять промежуток, где
x часть графика выше оси Ох.
0,5 3
Ответ: [-0,5; -3].
10

11. Повторение

Дискриминант – различитель можно найти
по формуле D b 2 4ac
Так как D>0, то уравнение имеет два корня.
Корни квадратного уравнения можно
вычислить по формулам: x1, 2 b D
2a
11

12. Модуль «Алгебра»

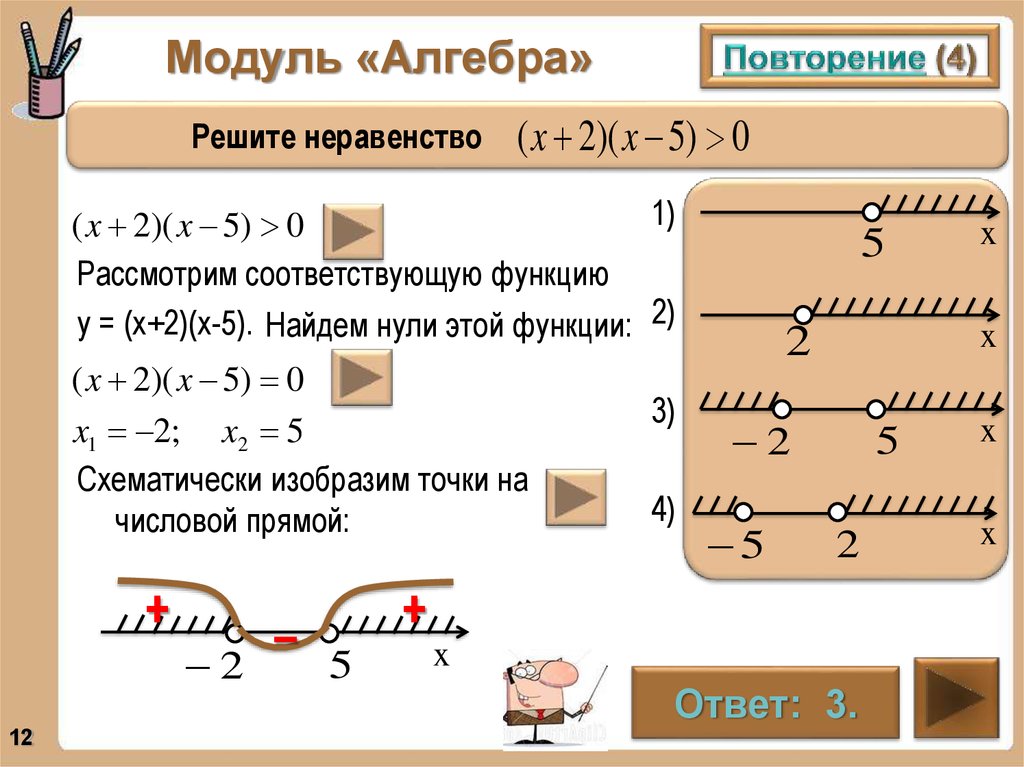
Решите неравенство
( x 2)( x 5) 0
1) .
( x 2)( x 5) 0
Рассмотрим соответствующую функцию
у = (х+2)(х-5). Найдем нули этой функции: 2) .
( x 2)( x 5) 0
x1 2; x2 5
Схематически изобразим точки на
числовой прямой:
+
2
12
–
3) .
5
x
2
2
5
4) .
5
2
+
5
x
x
Ответ: 3.
x
x

13. Повторение

Неравенства вида (х-a)(x-b)(x-c)∙…>0
решаются методом интервалов.
Произведение равно нулю тогда, когда один
из множителей равен нулю (при условии, что
другие множители не теряют смысла)
В данных неравенствах знаки на промежутке
постоянен, и меняются при переходе через
нуль функции.
Если в неравенстве вида (х-a)(x-b)(x-c)∙…>0 во
всех скобках коэффициенты при х равны +1 и
a≠b≠c то можно расставить знаки на
промежутках таким образом: на самом правом
ставится знак «+», а далее знаки чередуются
13

14. Модуль «Алгебра»

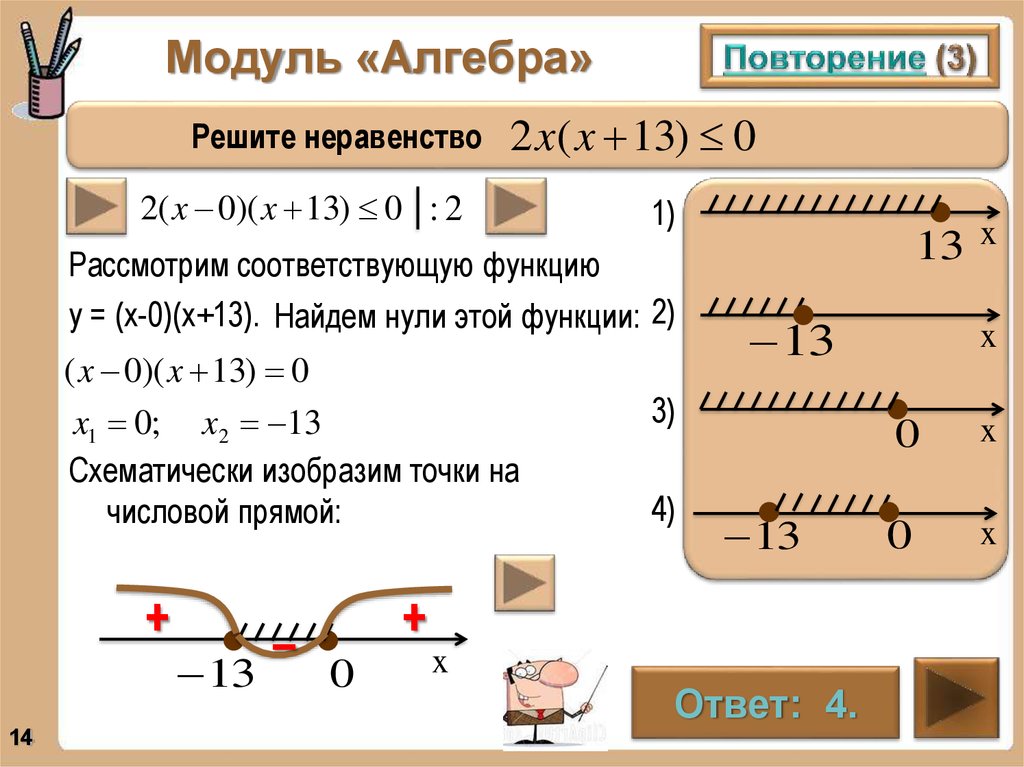
Решите неравенство
2 x( x 13) 0
2( x 0)( x 13) 0 : 2
1) .
Рассмотрим соответствующую функцию
у = (х-0)(х+13). Найдем нули этой функции: 2) .
( x 0)( x 13) 0
x1 0; x2 13
Схематически изобразим точки на
числовой прямой:
+
14
13
–
13 x
13
3) .
4) .
13
+
0
x
Ответ: 4.
x
0
x
0
x

15. Повторение

В неравенстве 2х(х+13)≤0 множитель х
можно заменить множителем (х-0).
Если обе части неравенства разделить на
одно и тоже положительное число, то при
этом знак неравенства не меняется.
Т.к. неравенство содержит знак «меньше 0»,
то на рисунке надо взять промежуток, где
часть «кривой знаков» ниже оси Ох.
15

16. Модуль «Алгебра»

Сопоставьте между
А) х² > 100
собой неравенства и
Б) -х² ≤ 100
множества их
В) х ²≤ 100
решений.
õ2 100
2
õ
100
2
õ 100 0
x 2 100
( õ 10)( x 10) 0
Х – любое число.
y ( õ 10)( x 10)
( õ 10)( x 10) 0
õ 10
+
–
10
+
10
Ответ:
16
1)(-∞;∞)
2)(-∞;-10);(10;+∞)
3)(-∞;-10];[10;+∞)
4)[-10;10]
õ2 100
õ2 100 0
( õ 10)( x 10) 0
y ( õ 10)( x 10)
( õ 10)( x 10) 0
õ 10
+
x
10
А
2
Б
1
В
4
–
+
10
x

17. Повторение

Квадрат любого числа есть число
неотрицательное.
17

18. Модуль «Алгебра»

Решите неравенство
( x 2)( x 4)( x 5)
0
x 5
1)
( x 2)( x 4)( x 5)
0
x 5
2)
x 5 0
x 5
y ( x 2)( x 4)
+
+
( x 2)( x 4) 0
2
( x 2)( x 4) 0
x1 2;
–
x2 4
Ответ: (-∞;2);(4;5);(5;+∞)
18
45
x

19. Повторение

Чтобы сократить дробь, надо числитель и
знаменатель разделить на одно и то же
выражение, не равное нулю.
Так как знаменатель дроби не может
обращаться в нуль, то точка х=5 выпадает из
решения.
19