Похожие презентации:
Метод рационализации при решении неравенств. Урок повторения по алгебре в 11 профильном классе
1. Муниципальное бюджетное общеобразовательное учреждение лицей № 6 городского округа Тольятти
Метод рационализации прирешении неравенств
урок повторения по алгебре
в 11 профильном классе
Подготовила
Овчинникова Наталья Александровна,
учитель математики высшей категории
МБУ лицея №6 г. о. Тольятти
2. Метод рационализации неравенств известен около 50 лет, встречался под названиями: - метод декомпозиции; - метод замены
множителей;- обобщение метода интервалов
3. Данный метод позволяет с помощью условий равносильности сводить решение целых классов сложных неравенств к решению простых
рациональных неравенствклассическим методом интервалов.
4.
Идея метода рационализациисостоит в использовании свойств
монотонной функции.
Доказательства равносильных переходов
приведены в пособии:
МАТЕМАТИКА ЕГЭ 2014.
РЕШЕНИЕ НЕРАВЕНСТВ С ОДНОЙ
ПЕРЕМЕННОЙ (типовые задания С3)
Прокофьев А.А., Корянов А.Г.
5. http://alexlarin.net/ege/2014/C3-2014.pdf
6. Суть метода рационализации заключается в замене сложного выражения F(x) на более простое выражение G(x) (в конечном счете,
рациональное),при которой неравенство G(x) 0
равносильно неравенству F(x) 0
в области определения выражения
F(x).
где
- один из знаков <, >, ≤, ≥
7.
Метод рационализации используют ипри решении неравенств вида:
f1 ( x) f 2 ( x) ... f k ( x)
F ( x)
0
g1 ( x) g 2 ( x) ... g l ( x)
Любой из множителей можно заменять
на совпадающий с ним по знаку
8.
Таблица замены множителей№
Выражение F
1.
log h f log h g
2.
log h f log p g 0
Выражение G
h 1 f g 0
h 1 f 1 p 1 g 1 0
3.
4.
5.
h h
f
g
f g
f g
h 1 f g 0
f g
f g f g 0
- один из знаков <, >, ≤, ≥
9.
Пример 1log 5 x
x 2
4
4
x 5
5 х 0
5 x 1
х 2 0
5 x 1 x 2 1 0
log 5 x x 2 4 4
log 5 x x 2 0
Ответ : 1;4
10.
Пример 2log x 3 x log x 4 x log x x 7 x 12 1 0
2
Решение :
log x 3 x log x 4 x log x 3 x log x 4 x 1 0
log x 3 x 1 log x 4 x 1 0
х 0
x 1
3 x 0
x 1 2 3 x 1 4 x 1 0
Ответ : 0;1 1;1,5 2;3
11.
Пример 3log 2 x 2 x 3 x 1 log 2 x x 2 3 2 x 0
2 x 2 x 0
2
2 x x 1
3 x 1 0
2
2
x
x
0
2 x x 2 1
3 2 x 0
2
2
(
2
x
x
1
)(
3
x
1
1
)(
2
x
x
1)( 3 2 x 1) 0
2
Ответ : ;1 1;1,5
3
12.
Пример 4log x 2 4 7 x 2 x 2
2
x 2 0
x 2 1
2
4 7 x 2 x 0
x 2 1 4 7 x 2 x 2 ( x 2) 2 0
13.
х 2, х 1, х 30,5 х 4
x 2 1 x 2 1 3x 3x 2 0
0,5 х 4
3х х 1 х 3 х 1 0
Ответ : 0,5;0 1;4
14.
Пример 5log 4 х2 12х 8 4 х 5 0
Заменим данное неравенство равносильной системой,
используя метод рационализации:
( 4 x 2 12 x 8 1)( 4 x 5 1) 0
4 x 2 12 x 8 0
2
4 x 12 x 8 1
4 x 5 0
(2 x 3) 2 (( 4 x 5) 2 1) 0
( x 1)( x 2) 0
5
3
x , x
4
2
15.
Окончательно получаем, что решением являются все х такие,что
5 5 3
х 1; ;
4 4 2
Ответ:
5 5 3
х 1; ;
4 4 2
16.
Пример 6x
2
2 x 2
2 x 2 x 1
x 2 x 2
2
9 x 2
x 2x 2 0
2
2
2
x 2 x 2 1 2 x x 1 9 x 0
2
Ответ : 3; 1 3 1;2
17.
Пример 7Для каждого значения параметра а
найти решения неравенства
x
sin x
a
sin x
log a x x log a x
,
x
a
удовлетворяющие условию
Решение:
x
2
18.
xsin x
a
sin x
log a x x log a x
x
a
0 x
2
a 0, a 1
sin x
a
sin x
x log a x x log a a log a x x 0
x
sin x
log a x x x log a x x
a
a
sin x
log a x 1 x x 0
a 1 x a x 1 sin x a 0
sin x
a
0
19. Список используемых источников: 1. Прокофьев А.А., Корянов А.Г. Материала курса «Готовим к ЕГЭ хорошистов и отличников»: лекции
1 – 4 . М.: Педагогическийуниверситет «Первое сентября», 2012
https://edu.1september.ru/distance/
20. Список используемых источников: 2. Коропец З.Л. , Коропец А.А. , Алексеева Т.А. Математика. Нестандартные методы решения
неравенств и их систем.Орел, 2012
3. Прокофьев А.А. Корянов А.Г.
Математика ЕГЭ 2014.
Решение неравенств с одной
переменной (типовые задания С3)
http://alexlarin.net/ege/2014/C3-2014.pdf











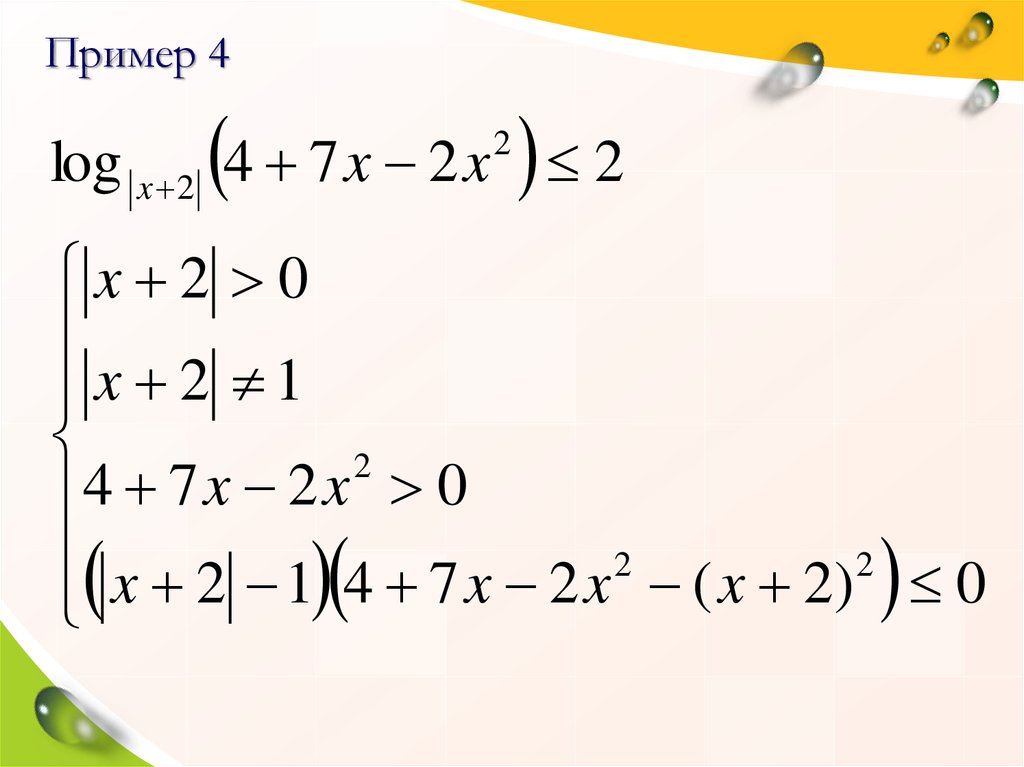
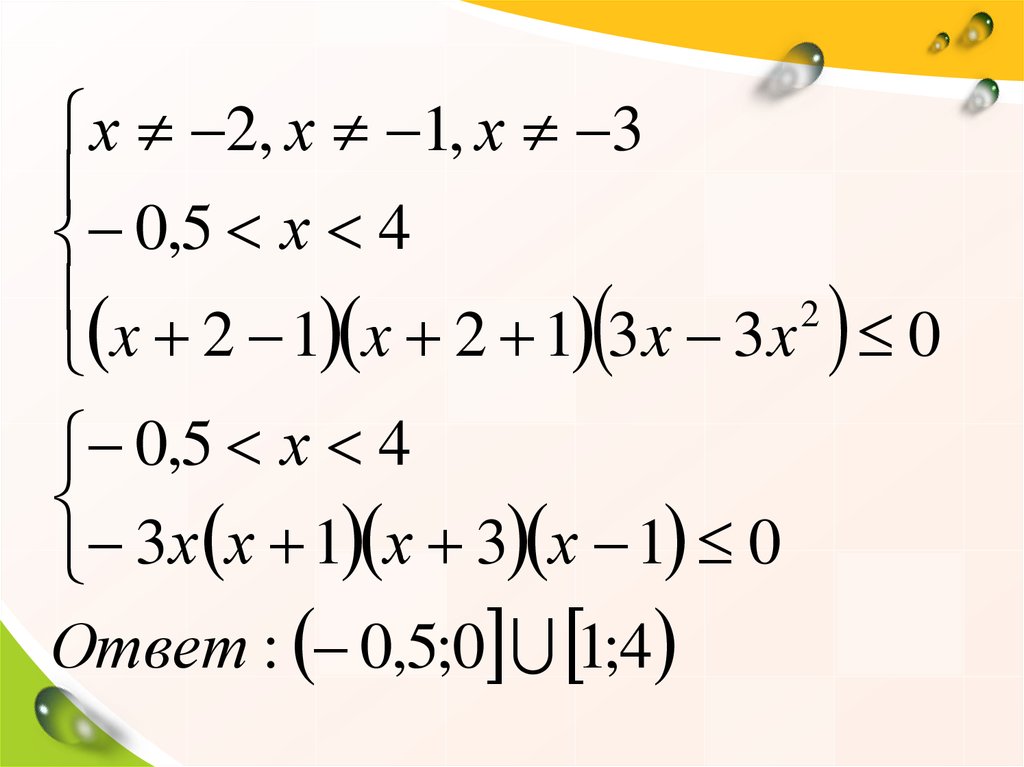







 Математика
Математика








