Похожие презентации:
Решение логарифмических неравенств с помощью метода рационализации
1. Решение логарифмических неравенств с помощью метода рационализации
Готовимся к ЕГЭ (задание С3)Решение логарифмических
неравенств
с помощью метода
рационализации
2.
Суть метода рационализации длярешения логарифмических неравенств
(метода замены множителя) состоит в
том, что в ходе решения осуществляется
переход от неравенства, содержащего
логарифмические выражения, к
равносильному рациональному
неравенству (или равносильной системе
рациональных неравенств).
Примечание.
В вариантах ЕГЭ в 2012 году в задании С3 необходимо было решить систему
неравенств. За верное решение только одного неравенства предложенной системы,
согласно разработанным критериям, эксперты ЕГЭ ставили 1 балл.
3.
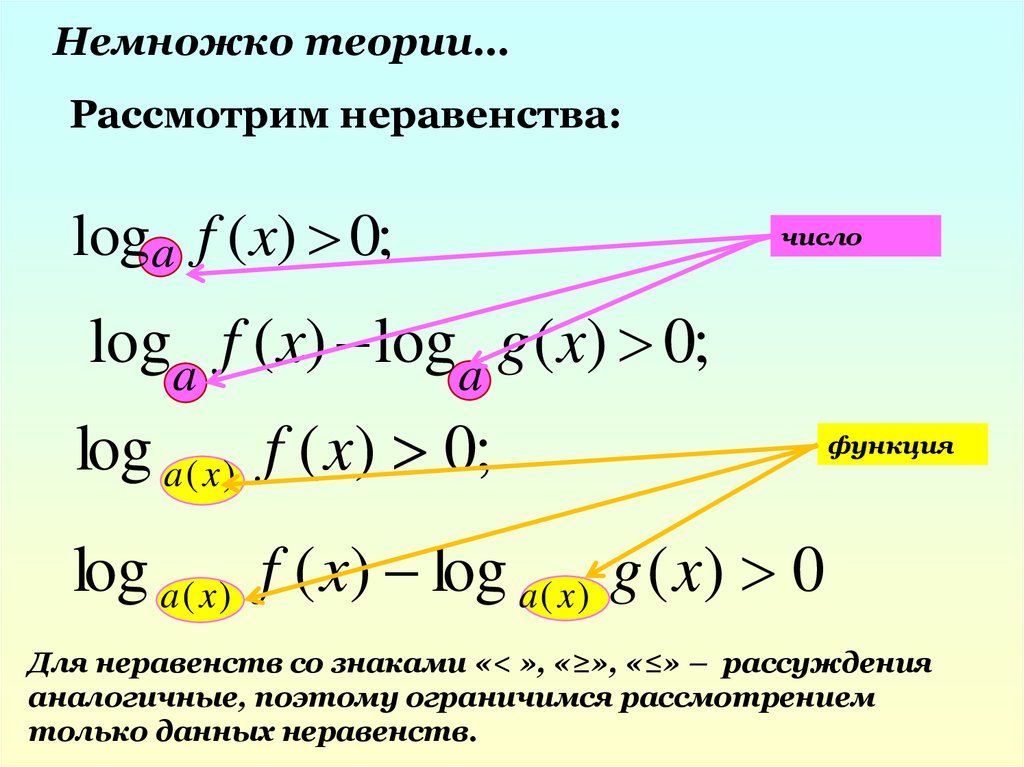
Немножко теории…Рассмотрим неравенства:
loga f ( x) 0;
число
loga f ( x) loga g ( x) 0;
log a ( x ) f ( x) 0;
функция
log a ( x ) f ( x) log a ( x ) g ( x) 0
Для неравенств со знаками «< », «≥», «≤» – рассуждения
аналогичные, поэтому ограничимся рассмотрением
только данных неравенств.
4.
1) loga f ( x) 0, a 0, a 1.log a f ( x) log a 1.
Если а 1, то f ( x) 1, значит,
(a 1) ( f ( x) 1) 0;
Если 0 a 1, то 0
(a 1) ( f ( x) 1) 0.
Следовательно :
logЗнак
a t возрастает на R
f («сохраняется».
x) 1, значит,
Имеем : a 1 0; f ( x) 1 0.
log a t убывает на R
Имеем : a 1 0; f(x) 1 0.
(a 1) ( f ( x) 1) 0,
log a f ( x) 0
f ( x) 0.
5.
loga f ( x) loga g ( x) 0, a 0, a 1.loga f ( x) loga g ( x),
Если a 1, то f ( x) g ( x) 0, тогда
(a 1)( f ( x) g ( x)) 0,
Знак
Если 0 a 1, то 0 f ( x) g ( x), значит,
«сохраняется».
(a 1)( f ( x) g ( x)) 0.
Имеем :
log a f ( x) log a g ( x) 0
(a 1)( f ( x) g ( x)) 0,
f ( x) 0,
g ( x ) 0.
6.
(a 1) ( f ( x) 1)loga f ( x) 0;
loga f ( x) 0;
loga f ( x) loga g ( x) 0;
loga f ( x) loga g ( x) 0;
(a 1)( f ( x) g ( x))
При решении учитываем ограничения!
7.
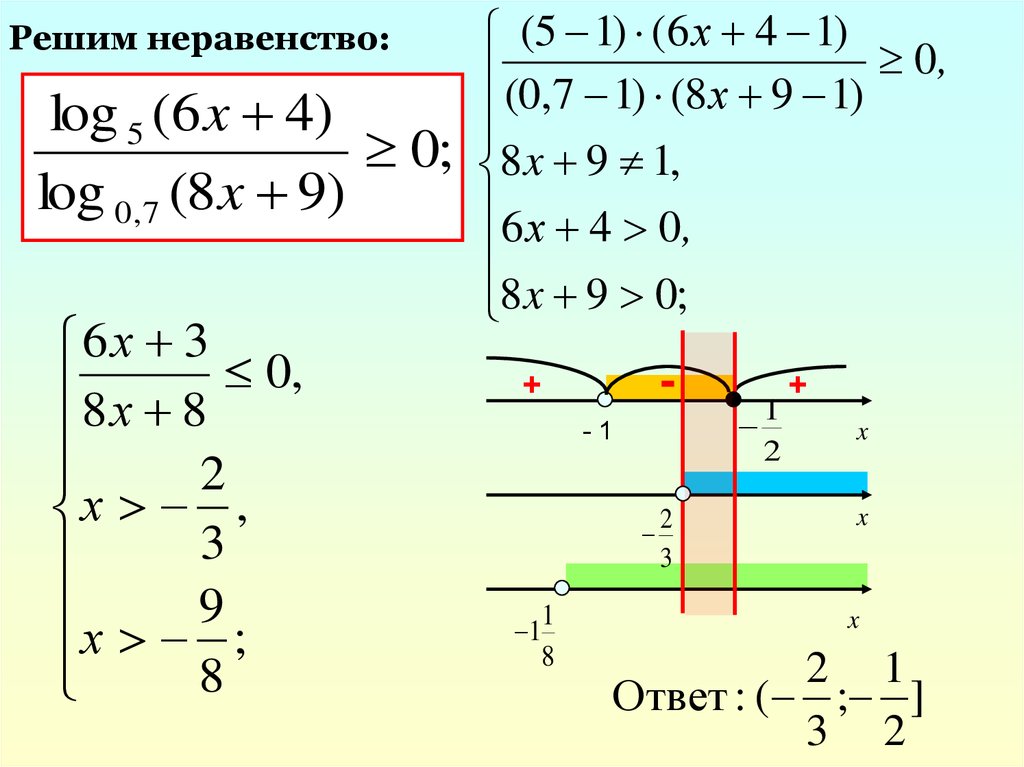
Решим неравенство:log 5 (6 x 4)
0;
log 0,7 (8 x 9)
6х 3
8 х 8 0,
2
х ,
3
9
х 8 ;
(5 1) (6 х 4 1)
(0,7 1) (8 х 9 1) 0,
8 x 9 1,
6 х 4 0,
8 x 9 0;
-
+
-1
1
1
8
2
3
1
2
+
x
x
x
2 1
Ответ : ( ; ]
3 2
8.
log a ( x ) f ( x) 0.Если a( x) 1, то f ( x) 1,
тогда (a( x) 1) ( f ( x) 1) 0.
Если 0 a( x) 1, то 0 f ( x) 1,
тогда (a( x) 1) ( f ( x) 1) 0;
log a(x) f(x) 0
Имеем:
(а( х) 1) (
a( x) 0,
a( x) 1,
f ( x) 0;
f ( x) 1) 0,
9.
log a ( x ) f ( x) log a ( x ) g ( x) 0,log a ( x ) f ( x) log a ( x ) g ( x)
Если a( x) 1, то f ( x) g ( x) 0,
тогда (a( x) 1) ( f ( x) g ( x)) 0.
Если 0 a( x) 1, то 0 f ( x) g ( x),
тогда (a( x) 1) ( f ( x) g ( x)) 0;
log a ( x ) f ( x) log a ( x ) g ( x) 0
Имеем: (a( x) 1)( f ( x) g ( x)) 0,
a( x) 0,
a( x) 1,
f ( x) 0,
g ( x) 0.
10.
Решим неравенство:Ограничения:
2 х 3 0,
2 х 3 1,
x 2 0;
log 2 x 3 x 1;
2
log 2 x 3 x 1
2
3
х 2 ,
х 1,
x 0.
log 2 x 3 x 1 0;
2
log 2 x 3 x log 2 x 3 (2 x 3) 0;
2
11.
log 2 x 3 x log 2 x 3 (2 x 3) 0;2
-1
(2 x 3 1) ( x
х 3 ;
2
х 1;
x 0;
2
2 x 3) 0,
(2 x 2)( х 1)( x 3) 0,
3
х ;
2
х 1;
x 0.
12.
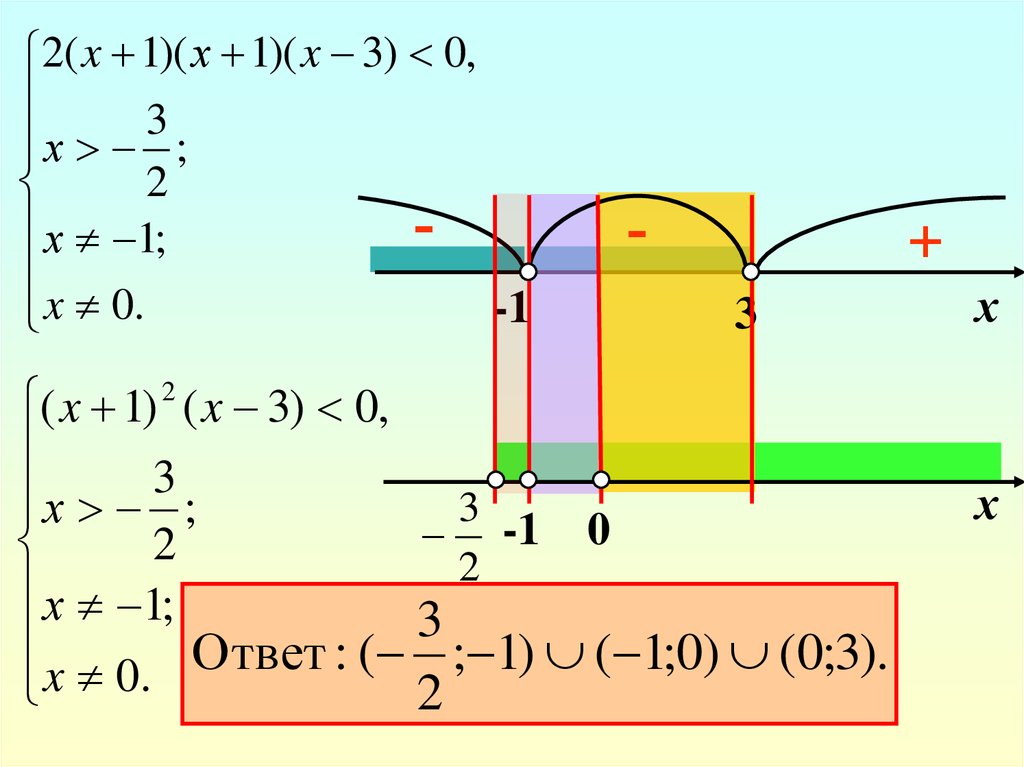
2( x 1)( х 1)( x 3) 0,3
х ;
2
х 1;
x 0.
-1
-
+
3
( x 1) 2 ( x 3) 0,
х 3 ;
3
-1 0
2
2
х 1;
3
x 0. Ответ : ( 2 ; 1) ( 1;0) (0;3).
х
х
13.
x 21;
2x 1
4
Решим неравенство:
log 2 x 1
Ограничения:
х 2
0,
2
x
1
2 х 1 0,
2 x 1 1;
4
1
x
,
2
1
х ,
2
x 1;
1
х ,
2
x 1;
14.
x 21;
2x 1
4
log 2 x 1
x 2
log 2 x 1 (2 x 1) 0;
2x 1
4
log 2 x 1
-1
x 2
2 x 1 1
(2 x 1) 0;
2x 1
4
2
x 2 4x 1
0;
2 x 2
2x 1
4
2
x 4x 3
0;
x 1
2x 1
4
15.
Решаем методом интервалов.x 4x 3
0;
x 1
2x 1
1
х ,
2
x 1;
4
+
3
-
2
+
1) х -
1
2
2) Нули функции :
х 1,
2
х 1,
х 2 3;
-
х 1,
х 1,
х 3.
+
-
-1 1
1
3
х
2
Ответ : [ 3; )
1
2
1
х
16. Пробный ЕГЭ. С-Петербург. 07.04.2012.
Решить неравенство :log
1
49
(26 5 x) log 6 x
1
1
7
Ограничения (ОДЗ) :
26
х
,
26 5 х 0,
5
6 x 0, x 6,
6 x 1; x 5;
26
,
х
5
x 5.
17.
log 1 (26 5 x) log 6 x49
1
1;
7
1
log 7 2 (26 5x) log 6 x 7 1;
1
log 7 (26 5 x) ( log 6 x 7) 1, ;
2
2 log (6 x)
log 7 (26 5x)
1
1 0;
2
log 7 (6 x)
log 7 (26 5 x) 2 log 7 (6 x)
0;
2 log 7 (6 x)
7
log 7 (26 5 x) log 7 (6 x)
0;
2 log 7 (6 x)
2
18.
log 7 (26 5 x) log 7 (6 x)0,
2 log 7 (6 x)
2
26 5 x (6 x) 2
0,
6 x 1
7-1>0
26 5 x 36 12 x x
0,
5 x
2
x 7 x 10
0,
x 5
2
( x 2)( x 5)
0,
x 5
19.
( x 2)( x 5)0
,
x 5
ОДЗ
26
,
х
5
x 5.
2
+
+
5
x
5 26
x
5
26
Ответ : 2;5 5; .
5
20. Практикум
Решите неравенства:1) log x 2 x 1 1;
6 x
2) log 0 ,25 x
1;
4
1
3) log 3 x
log 3 27 x 9 0;
27
2
2
4
x
3 x
4) log x 5
3;
log x 5
x 3
x
2
x 1
7 x
5) log x 8
;
1 log x 8
x 7
x 1
6) log 6 x
x4
0;
2
x 12 x 36
Практикум
21.
Ответык заданиям
«Клик» по нужному заданию даёт
переход к фрагменту решения и ответу
Назад - в «Практимум»
22.
log x 2 x 1 1;2
x 1 x 1 x 2 0,
х 0,
x 1,
x 1 .
2
2
1
Ответ : - 1;0 0; 1; .
2
Досрочный ЕГЭ
26.04.2012
23.
6 xlog 0 ,25 x 2
1
4
ЕГЭ - 2012. Запад.
07.06.2012
2
6
х
x
2
(
0
,
25
x
1) (
) 0,
4
x 6,
х 0,
x 2,
x 2.
Ответ : - ; 3 - 2;0 0;2 2;6 .
24.
log 3 x1
log 3 27 x 9 0
27
3 log 3 x 3 2 log 3 3x 9 0,
х 0,
1
x ;
3
log 3 x 3 1 0,
х 0,
1
x ;
3
ЕГЭ - 2012. Восток.
07.06.2012
3x 1 3 3x 0,
х 0,
1
x ;
3
1
Ответ : 0; 1; .
3
25.
4x
3 x
log x 5
3;
log x 5
x 3
x
ЕГЭ-2012.
Резервный день
«основной волны».
21.06.2012
x 3
3
log
3,
x 5
x
х
х 0,
Т.к.
0,то
x 3;
х 3
4
3
x
3 x
x 3
x 5,
log x 5
4 log x 5
.
4 log x 5
x
x
x
x 4;
x 3
x
5
1
x
5
0,
x
х 0,
x 3;
x 5,
x 4;
Ответ : - 5;-4 - 3;-1 3; .
26.
2ЕГЭ -2012.
«Вторая
волна».
10.07.2012.
x 1
7 x
log x 8
;
1 log x 8
x 7
x 1
x 7
x 7
2 log x 8
1 log x 8
;
x 1
x 1
x 7
log x 8
1 0;
x 1
x 2 8 х 15
0,
x 7
x 1
х 1,
x 7;
x 8,
Ответ : - 8;-7 - 5;-3 7; .
x 7;
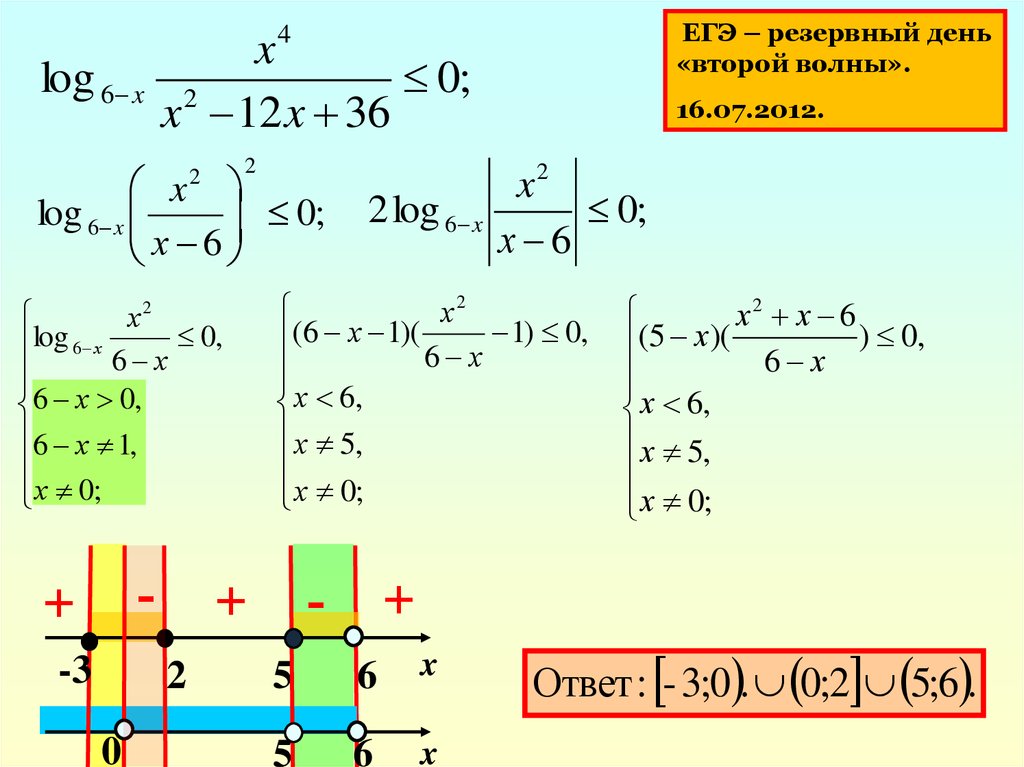
27.
ЕГЭ – резервный день«второй волны».
4
log 6 x
x
0;
2
x 12 x 36
2
x
0;
log 6 x
х 6
2
х2
0,
log 6 х
6 х
6 х 0,
6 х 1,
х 0;
-
+
-3
0
x2
0;
х 6
х2
1) 0,
(6 х 1)(
6 х
х 6,
х 5,
х 0;
+
2
2 log 6 x
16.07.2012.
х2 х 6
) 0,
(5 х)(
6 х
х 6,
х 5,
х 0;
+
5
6
x
5
6
x
Ответ : - 3;0 . 0;2 5;6 .
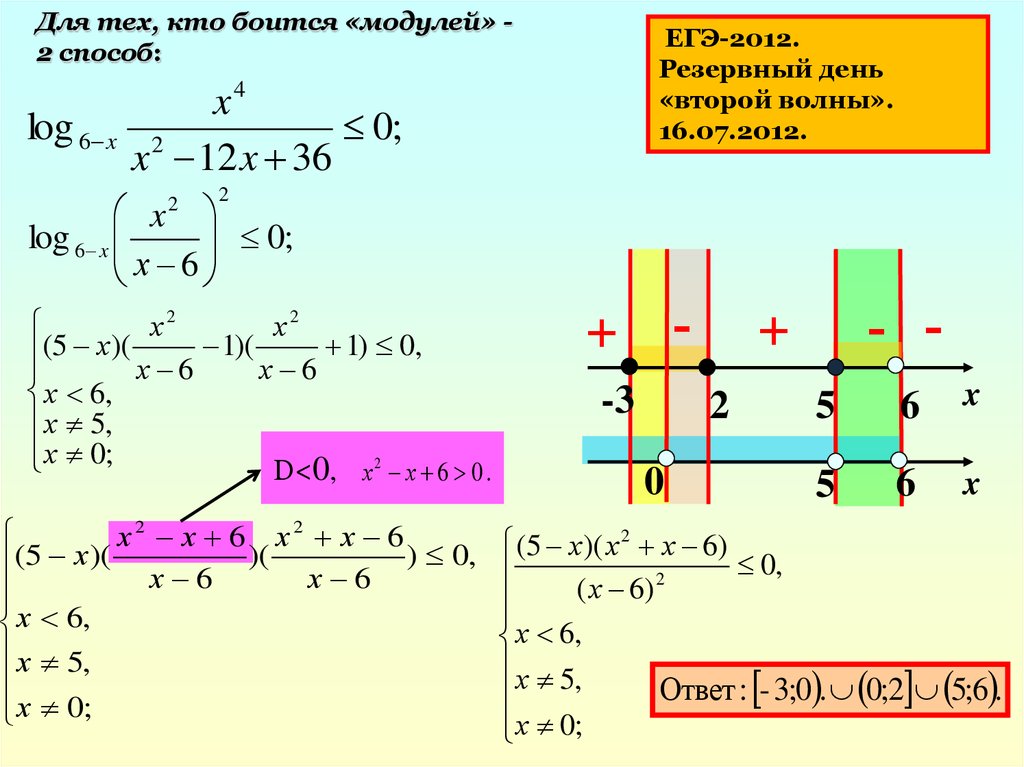
28.
Для тех, кто боится «модулей» 2 способ:log 6 x
ЕГЭ-2012.
Резервный день
«второй волны».
16.07.2012.
x4
0;
2
x 12 x 36
2
x
0;
log 6 x
х 6
2
х2
х2
1)(
1) 0,
(5 х)(
х 6
х 6
х 6,
х 5,
х 0;
D<0, х 2 х 6 0 .
х2 х 6 х2 х 6
)(
) 0,
(5 х)(
х 6
х 6
х 6,
х 5,
х 0;
-
+
-3
2
0
- -
+
5
6
x
5
6
x
(5 х)( х 2 х 6)
0,
2
( х 6)
х 6,
х 5,
Ответ : - 3;0 . 0;2 5;6 .
х 0;
29.
На память…Выражение (множитель)
в неравенстве
На что меняем
(правая часть неравенства равна
нулю!)
log a f log a g
(a 1) ( f g )
(помните, что f >0, g >0,a >0, a 1)
log a f 1
(a 1) ( f a)
(помните, что f >0, ,a >0, a 1)
log a f
(a 1) ( f 1)
(помните, что f >0, a >0 ,a 1)
Примечание: a – функция от х или число, f и g – функции от х.
30.
В презентации использовались ресурсы:1. Корянов А.Г., Прокофьев А.А. Интернет – ресурс:
http://alexlarin.net/ege/2011/C3-2011.pdf
2. ЕГЭ-2013: Математика: самое полное издание типовых
вариантов / авт.-сост. И.В. Ященко, И.Р. Высоцкий; под ред.
А.Л. Семенова, И.В. Ященко. – М.: АСТ: Астрель, 2013. -123 с.
– (Федеральный институт педагогических измерений).
3. Экзаменационные задания: http://alexlarin.net/








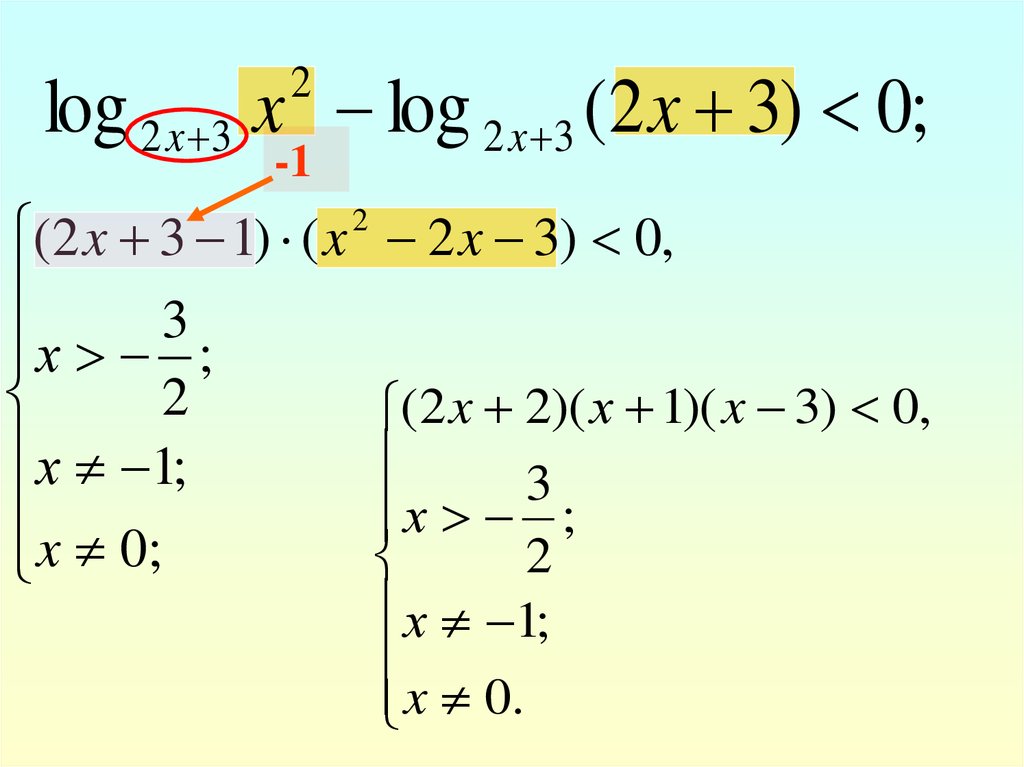

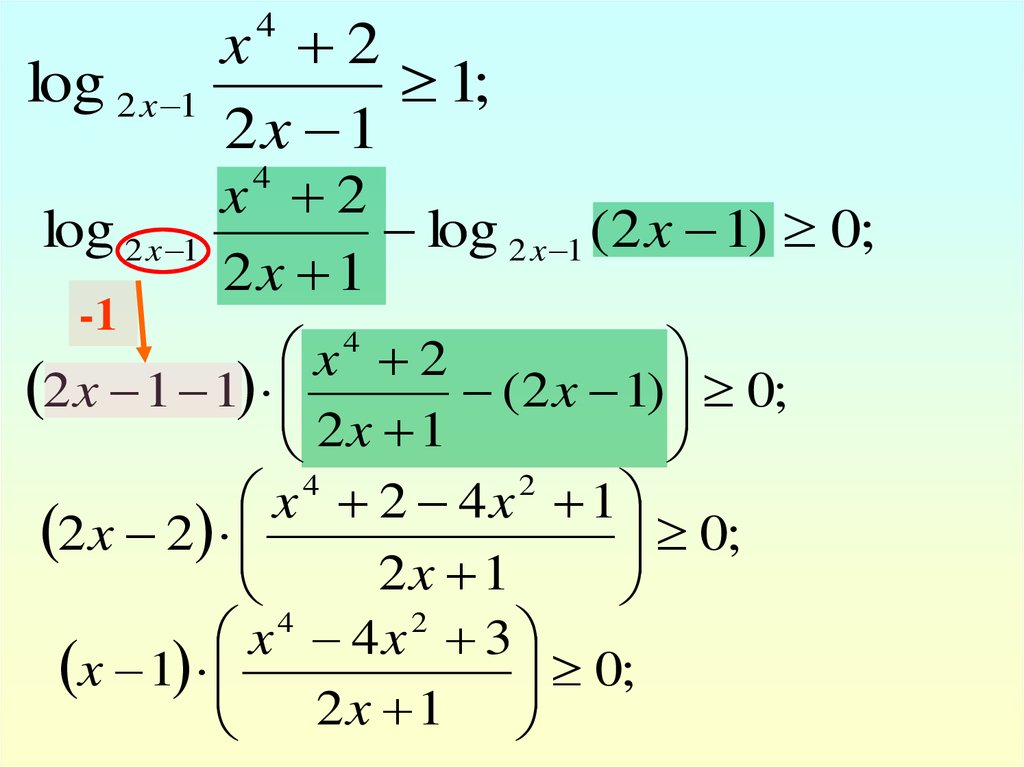



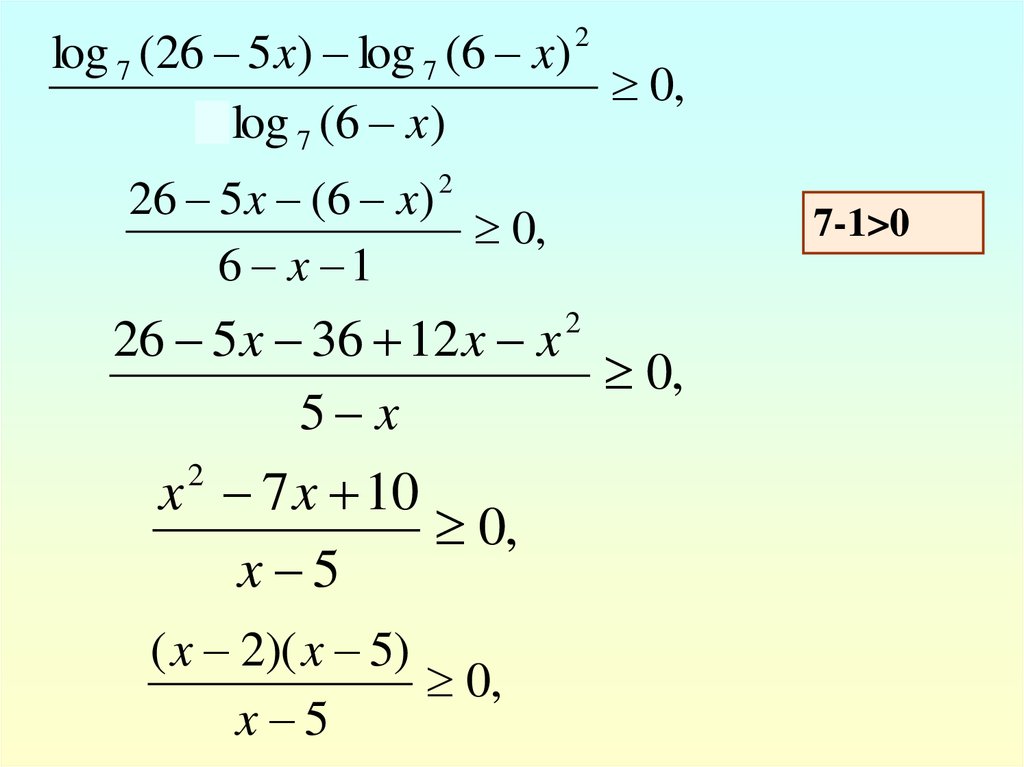










 Математика
Математика








