Свойства степени с рациональным показателем

1. Свойства степени с рациональным показателем.

“Пусть кто-нибудь попробует
вычеркнуть из математики
степени, и он увидит, что без
них далеко не уедешь”.

2. Задание на дом.

1. п 34, № 437-440 абв
2. Софизм по теме:
• сформулировать,
• придумать док-во
• разбор софизма

3. Вспомним теорию

1
Вспомним теорию
Арифметическим корнем n – ой степени (n N, n 2) из
неотрицательного числа a называется такое
неотрицательное число, n – я степень которого равна а:
2 n 1
2n
a
2 n 1
a
nk
2n
a
a,
mn
n N
n N
a ,
k
a
m
,
при
a 0

4.

2
1)
m
n
a
Если
n
Степень с рациональным
показателем.
m
0,
n
m Z , n N , a 0;
где
am ,
m
n
a n am
то
a 0.
при
2) При a > 0, b > 0, p и q - рациональные числа:
a a a
p
q
(a ) a
p q
p
a p a
( ) p
b
b
p q
pq
p
a
p q
a
q
a
(ab) a p b p
p

5.

Вспомним теорию
П
О
К
А
ВОЗ ВЕ
А
Т
Е
Л
Ь
Ч
Е
ДЕНИ Е
Т
И
Ы
Н
И О Р
Ц СТ ЕП
Н
А
О
ПР ОИЗ ВЕ ДЕ
А
ДЕ ЛЕ НИЕ
И
Е
По горизонтали:
1.Действие, с помощью которого
вычисляется значение степени
2. Произведение, состоящее из
одинаковых множителей .
3. Действие показателей степеней при
возведении степени в степень .
ЕНЬ
Д
И
НИЕ
И
Ц
А
4. Действие степеней, при которых
показатели степеней вычитаются .
По вертикали:
5. Число всех одинаковых множителей
6. Степень с нулевым показателем .
7. Повторяющийся множитель .
8. Значение 105 : ( 23 • 55 ) .
9. Показатель степени, который обычно не
пишут .

6. Тренировочные упражнения

5
1) Вычислить:
2
3 3 27 9 5
64
3
3
2) Найдите значение выражения
3) Упростить выражение
c c
5
c
1
5
5
=-26,5
6 2 17 5 6 2 17 = -2
=1
4
4) Найдите значение выражения
(
2с
2с
d
d
5) Упростить выражение
2c
2c
d
) (
d
1
2
d
2c
1
3
1
2
2c
)
d
125 8 5 5 49
1
2
6) Упростить выражение
a 2 2 a 1 a 2 2 a 1
2
2
2
2
= 2
=
4
= 7 5 35

7. Дешифратор Фамилия немецкого математика, который ввел термин - “показатель степени”.

Л Т Н Р Ш О Ь И Е Ф К А Д Ю
9\4 9
5 11 -2 4\9 20 5\3 1\3 1
3
8 64 2
1) -81\3 2) 811\2 3) (3\5)-1 4) (5\7)0 5) 27-1\3 6) (2\3)-2 7) 161\2 * 1251\3
Слово: 1) 2) 3) 4) 5) 6) 7)
-2 9 5/3 1 1/3 9/4 20
ШТ И Ф Е Л Ь

8. Михаэль Штифель

Немецкий
математик 15-16
века Один из
изобретателей
логарифмов

9. Дешифратор Фамилия французского математика, который ввел современную запись степеней.

Л Т Н Р Ш О Ь И Е Ф К А Д Ю
9\4 9
5 11 -2 4\9 20 5\3 1\3 1
3
8 64 2
1) Х1\3=4 2) у-1= 3 3) ( х+6)1\2 = 3 4) у1\3 =2 5) (у-3)1\3=2 6) а1\2 : а = 1\3
Слово: 1) 2) 3) 4) 5) 6)
64 1/3 3 8 11 9
Д Е К А Р Т

10. РЕНЕ ДЕКАРТ (17 ВЕК)

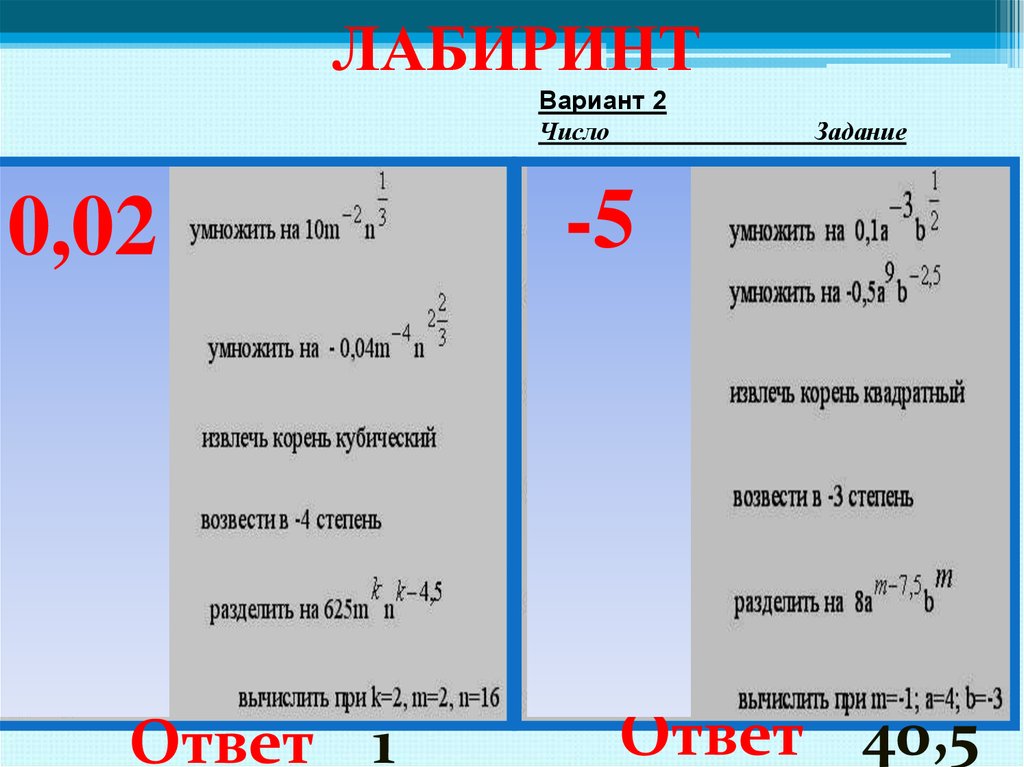
11. ЛАБИРИНТ

Вариант 2
Число
-5
0,02
ВАРИАНТ 1
Число
Задание
Задание
Ответ 1
Ответ 40,5

12.

Задания для самостоятельной работы
Вычислить: 1)
2)
3)
4)
5)
2
3) :
3
5( 27
(( 4 2 4 8 ) 2 6)(( 4 2 4 8 ) 2 6)
8 28 8 28
64
5
6
(0,125)
1
3
4
32 2 16
1
1
2
(3 ) 4
0 4
(3 100 23 5 23 2 )( 3 10 3 4 )
Упростить:
6)
3
b b
3
7)
(
0,5а
1
4
(2 а)
3
4
b
2
4
1
4
(2 а) а
2
3
4
) : ( 2а а 2 )
3
4

13.

Проверка
1)
2)
2
5
(
3
3
3
)
3
5( 27 3 ) :
15
3
2
(( 2 8 ) 6)(( 2 8 ) 6)
4
2
4
4
4
2
( 2 8 2 2 8 6)( 2 8 2 2 8 6)
4
4
( 2 8 2)( 2 8 2) ( 2 8 ) 4
2
2 8 2 16 4 14

14.

Проверка
3)
8 28 8 28
1 2 7 7 1 2 7 7 (1 7 ) 2 (1 7 ) 2
1 7 1 7 7 1 1 7 2
4)
5
6
1
3
64 (0,125) 32 2 4 16
5
6
6
(2 )
1
3 3
(0,5 )
4
1
1
2
(30 ) 4 4
3
4
2
2 2 (2 )
5
1 4
1 1
6
5
5
2 ( ) 2 2 4 2 2 2 4 2
2
5

15.

5)
Проверка
3
3
3
3
3
( 100 2 5 2 2 )( 10 4 )
(а аb b )(a b) a b следует
3
3
3
3
( 10 ) ( 4 ) 10 4 6
По формуле
b3 b 2
6)
3
b
4
2
2
2 4
1
3 3
b
3
1
3
b
3
3
b

16.

Проверка
(
7)
0,5а
1
4
(2 а )
1
4
3
4
3
4
1
4
2 0,5a (2 a) (2 a) a
2 (2 a)
3
4
2)
3
4
3
(2 а ) а
) : ( 2а а 2 ) 4
2
1
4
1)
1 a (2 a)
3
4
a (2 a)
3
4
3
4
1
3
4
3
4
1
1
3
4
a (2 a)
3
4
;