Похожие презентации:
Решение логарифмических уравнений
1. Решение логарифмических уравнений
2. Простейшее логарифмическое уравнение
log a x b x a , x 0b
Например:
log 3 x 2
x 3
2
x 9;
Ответ : 9
( x 0) *
3.
№1. Решить уравненияx 1 0
a) log 2 x 1 3
log 2 x 1 log 2 2
3
x 1*
x 1 8
x 7
Ответ : 7
4.
б) log 2 x 1 log 2 x 3 3log 2 x 1 x 3 log 2 23
x 1 0
x 1
x 1*
x 3 0 x 3
x2 4x 3 8
x2 4x 5 0
x1 1
x2 5 исключено *
Ответ :1
5.
в) lg x 3 2 lg 2 lg xРешение
г ) log 7 36 log 7 3x 12 log 7 4
Решение
д) log x log 4 x 1,5 0
2
4
Решение
Далее
6. Решение уравнения под буквой в
в) lg x 3 2 lg 2 lg xx 3 0 x 3
x 0*
x 0
x 0
lg x 3 lg x lg 22
lg x x 3 lg 4
Согласно свойству:
p log a b log a b p
x 2 3x 4
x 2 3x 4 0
x1 1;
x2 4 ; исключено *
Ответ :1
Назад
7. Решение уравнения под буквой г
г ) log 7 36 log 7 3x 12 log 7 4log 7 3 x 12 log 7 36 log 7 4
36
log 7 3 x 12 log 7
4
3 x 12 9
3 x 12 0
3 x 12
x 4*
3 x 21
x 7;
Ответ : 7
Назад
8. Решение уравнения под буквой д
д) log 24 x log 4 x 1,5 0x 0*
log 4 x 1,5
1
log x log 4 x 1,5 0
2
Обозначим : log 4 x t
x 4 1,5
2
4
x
1
4
t 0,5t 1,5 0
2
t1 1
log 4 x 1
t 2 1,5
x 4
x
3
2
1
43
1
x
8
Ответ : 0,125;4
Назад
9. Решение уравнений с разными основаниями
а) log a x loga
2 log 1 3
x 0*
a
log a x log
1
a2
2 log a 1 3
1
1
log a x log a 2 log a 3
1
1
2
log a x 2 log a 2 log a 3
22
log a x log a
3
4
x
3
Опираясь на свойство:
1
log a q b log a b
q
4
Ответ :
3
10.
7б ) log x 2 log 4 x 0
6
1
1
7
log 2 x 0
log 2 x 2
6
6 3 log 22 x 7 log 2 x 0
3 log 22 x 7 log 2 x 6 0
Обозначим : log 2 x t
3t 2 7t 6 0
D 7 4 3 6 121
x 0
x 0;1 1; *
x 1
Опираясь на свойство:
1
log a b
log b a
log 2 x 3
x 8
2
7 11
3
6
7 11
2
t2
6
3
log 2 x
x 2
t1
x
1
Ответ : 3 ;8
4
2
3
1
3
4
2
3
11. Задание из пособия по подготовке к ЕГЭ Найти наибольший корень уравнения:
а)2 log x 1 3 3 log 3 x 1 5 0Ответ: 8
б )2 log 3 x 1 4 log 2 3x 1 3 0
Ответ: 5
в)2 x log 2 x 3 3 log 2 x 2 6 x 9 4 x 12
Ответ: 7



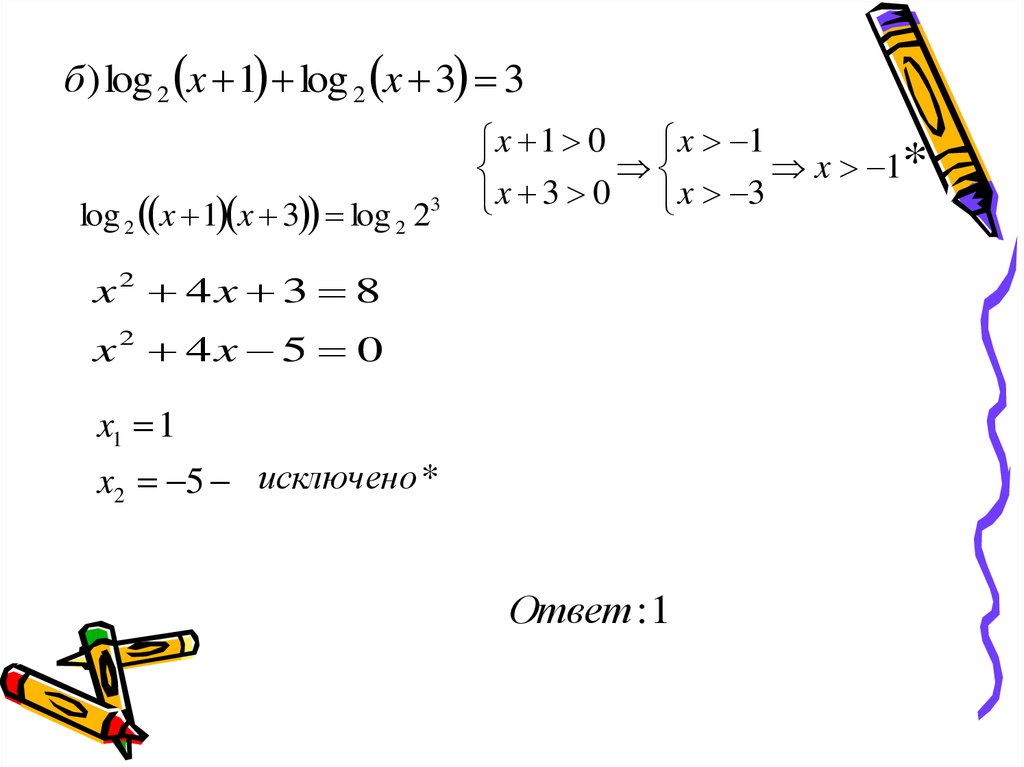





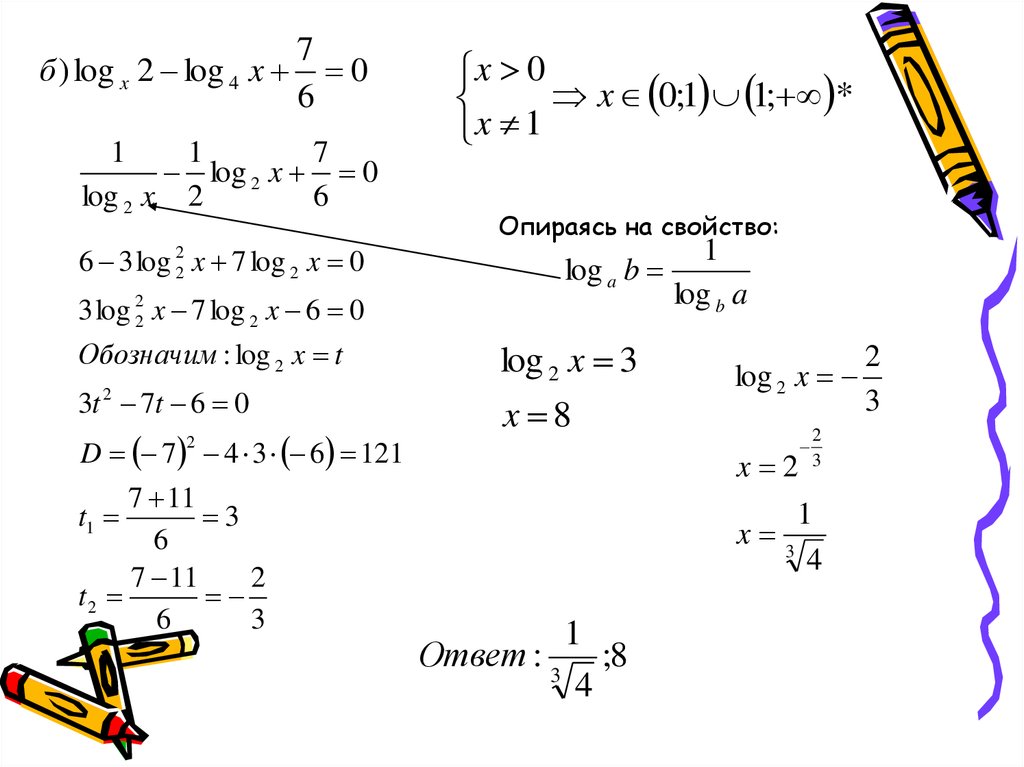

 Математика
Математика








