Похожие презентации:
Графический способ решения систем уравнений
1.
Графический способ решения систем уравненийПодготовил учитель математики Данилов С.Р.
2.
Дорогие друзья!Эта презентация поможет Вам научиться решать
системы уравнений с двумя переменными одним
из самых простых и наглядных способов –
графическим.
Но этот способ напрямую связан с построением
графиков уравнений, входящих в ту или иную
систему, поэтому для начала будет полезно
вспомнить, как выглядят графики основных
известных Вам элементарных функций.
Итак…
Дальше
3.
уВы, конечно, помните, что
графиком функции называют
множество всех точек
координатной плоскости,
абсциссы которых равны
значениям аргументов, а
ординаты –
соответствующим значениям
функции.
у = f(х)
х
0
Вы уже знакомы с некоторыми
важными видами функций
Дальше
4.
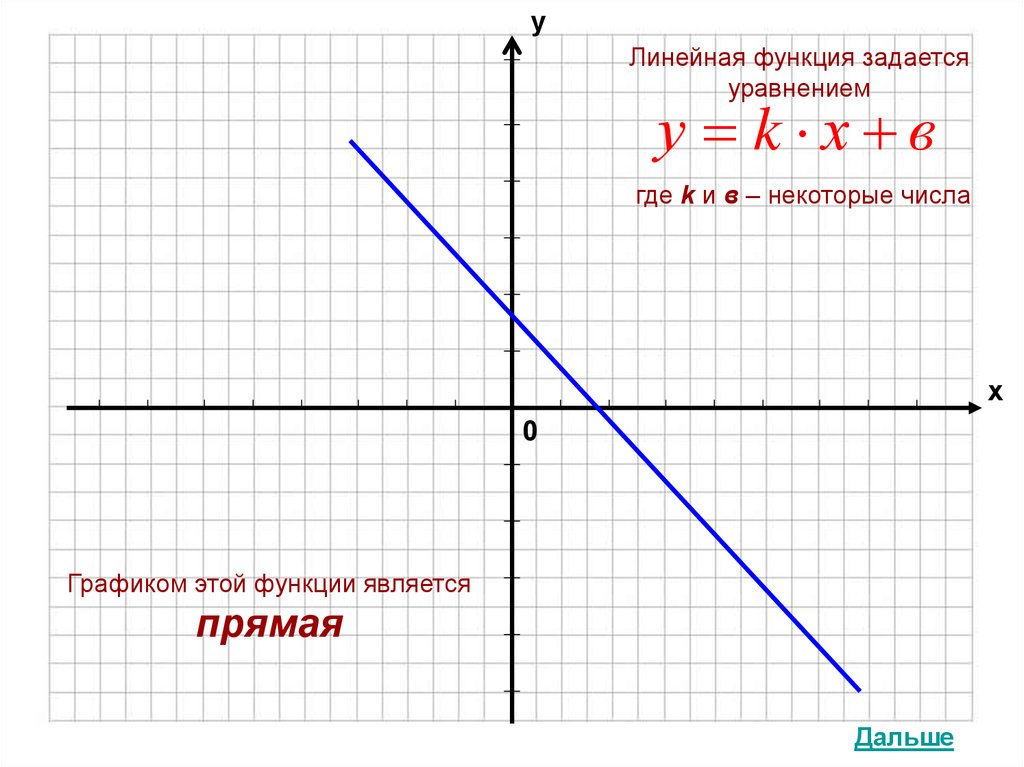
уЛинейная функция задается
уравнением
у k х в
где k и в – некоторые числа
х
0
Графиком этой функции является
прямая
Дальше
5.
уФункция обратной
пропорциональности
k
у
х
, где k 0
х
0
График этой функции называется
гиперболой
Дальше
6.
уРассмотрим функцию
( х а) 2 ( у в) 2 r 2
где а, в и r – некоторые числа
r
А
а
в
х
0
Графиком этой функции является
окружность
радиуса r с центром в т. А (а;в)
Дальше
7.
Квадратичная функцияу
у а х в х с
2
где а,в,с – некоторые числа и
а 0
в
2а
х
0
Графиком этой функции является
парабола
Дальше
8.
Графиком уравнения с двумя переменныминазывается, как вы знаете, множество точек
координатной плоскости, координаты которых
обращают уравнение в верное равенство.
Причем иногда уравнения могут быть достаточно
сложными, а графики таких уравнений – очень
необычными по форме.
Давайте рассмотрим несколько примеров таких
уравнений, используемых в высшей математике.
Дальше
9.
уРассмотрим, например,
уравнение
у 2 (а х) х 2 (а х)
0
Графиком этого уравнения будет
кривая, называемая
строфоидой
Дальше
10.
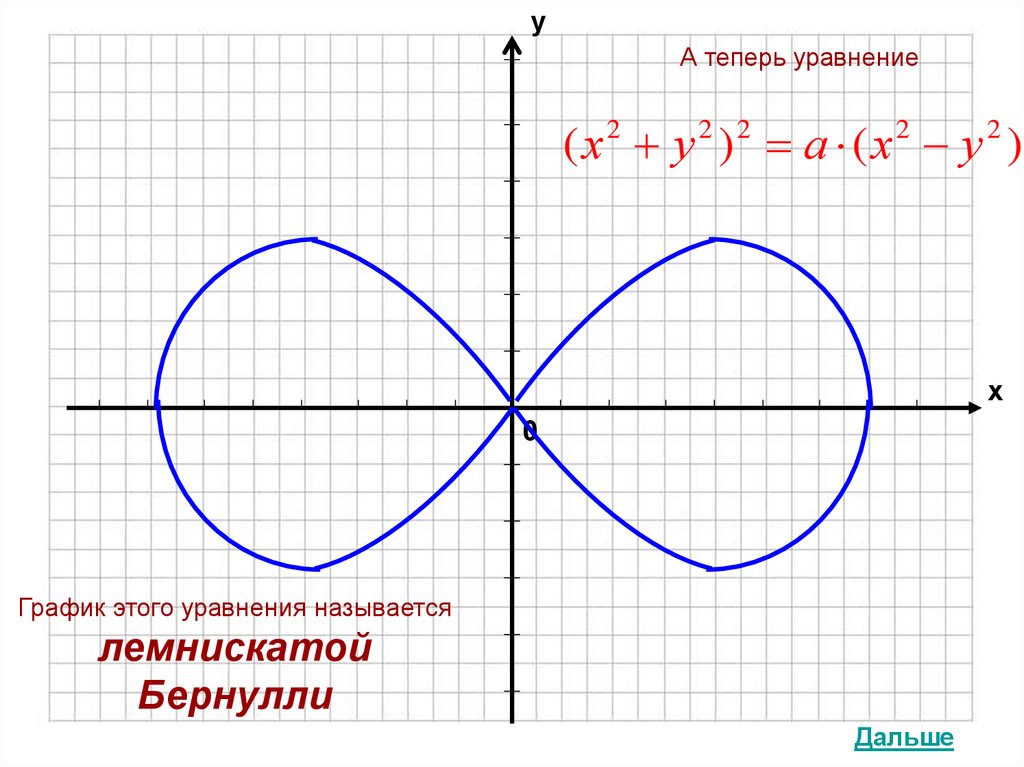
уА теперь уравнение
(х у ) а (х у )
2
2 2
2
2
х
0
График этого уравнения называется
лемнискатой
Бернулли
Дальше
11.
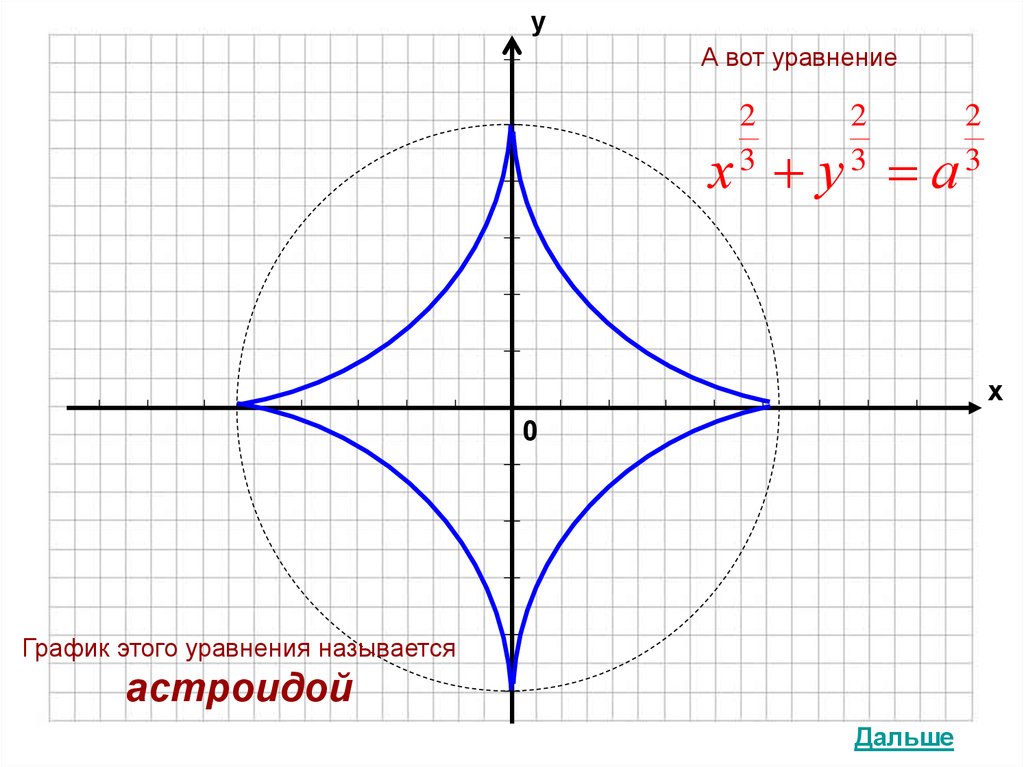
уА вот уравнение
2
3
2
3
х у а
2
3
х
0
График этого уравнения называется
астроидой
Дальше
12.
уСледующий пример:
( х 2 у 2 2ах) 2 4а 2 ( х 2 у 2 )
х
0
Эта кривая называется
кардиоидой
Дальше
13.
Конечно, Вам придется иметь дело с уравнениямипопроще, и, тем не менее, графики их нужно уметь
строить.
!
А теперь к делу – учимся решать системы
уравнений с двумя переменными
графически!
Уравнение 1,
Уравнение 2;
!
?
Дальше
14.
Пусть требуется решить системууравнений:
х2 + у2 = 25,
у = -х2 + 2х + 5;
Построим в одной системе
координат графики уравнений
х2 + у2 = 25 и у = -х2 + 2х + 5
Координаты любой точки окружности
являются решением уравнения
х2 + у2 = 25, а координаты любой
точки параболы являются решением
уравнения у = -х2 + 2х + 5.
Значит, координаты каждой из точек
пересечения окружности и параболы
удовлетворяют как первому
уравнению системы, так и второму,
т.е. являются решением системы.
Находим по рисунку значения
координат точек пересечения
графиков: А(-2,2;-4,5), В(0;5),
х1 -2,2, у1 -4,5
С(2,2;4,5), D(4;-3). Тогда система
имеет 4 решения
х3 2,2, у3 4,5
Второе и четвертое из этих решений – точные,
а первое и третье – приближенные.
х2 0, у2 5
х4 4, у4 -3
Дальше
15.
Давайте сделаем из рассмотренного примеравыводы.
Чтобы решить систему двух уравнений с двумя
неизвестными, нужно:
Построить в одной системе координат графики
уравнений, входящих в систему;
Определить координаты всех точек пересечений
графиков (если они есть);
Координаты этих точек и будут решениями системы.
Помните о двух вещах!
1. Если точек пересечения графиков нет, то система решений не имеет;
2. Координаты точек пересечения определяются приблизительно, поэтому и
решения могут получиться приблизительными;
Чтобы проверить точность полученных решений, их нужно подставить
в уравнения системы!
Дальше
16.
Решаем систему:Задание 1
у
ху 3,
3 х у 0;
у 3х
Преобразуем уравнения
системы:
3
у ,
х
у 3х;
у
1
3
х
1
0
х
Строим в одной системе
координат графики уравнений
системы
А теперь самостоятельно
определите решения системы.
Дальше
17.
Решаем систему:у
у х 2 0,
х у 2 0;
Задание 2
у х2
Преобразуем уравнения
системы:
у х2 ,
у х 2;
1
1
х
0
Строим в одной системе
координат графики уравнений
системы
у х 2
А теперь самостоятельно
определите решения системы.
Дальше
18.
уЗадание 3
Перед Вами графики двух
уравнений. Запишите систему,
определяемую этими
уравнениями, и ее решение.
х-у=1
1
1
х
0
3х+2у=18
Дальше
19.
уЗадание 4
Перед Вами графики двух
уравнений. Запишите систему,
определяемую этими
уравнениями, и ее решение.
у 2х
у
1
1
2
х
х
0
Дальше
20.
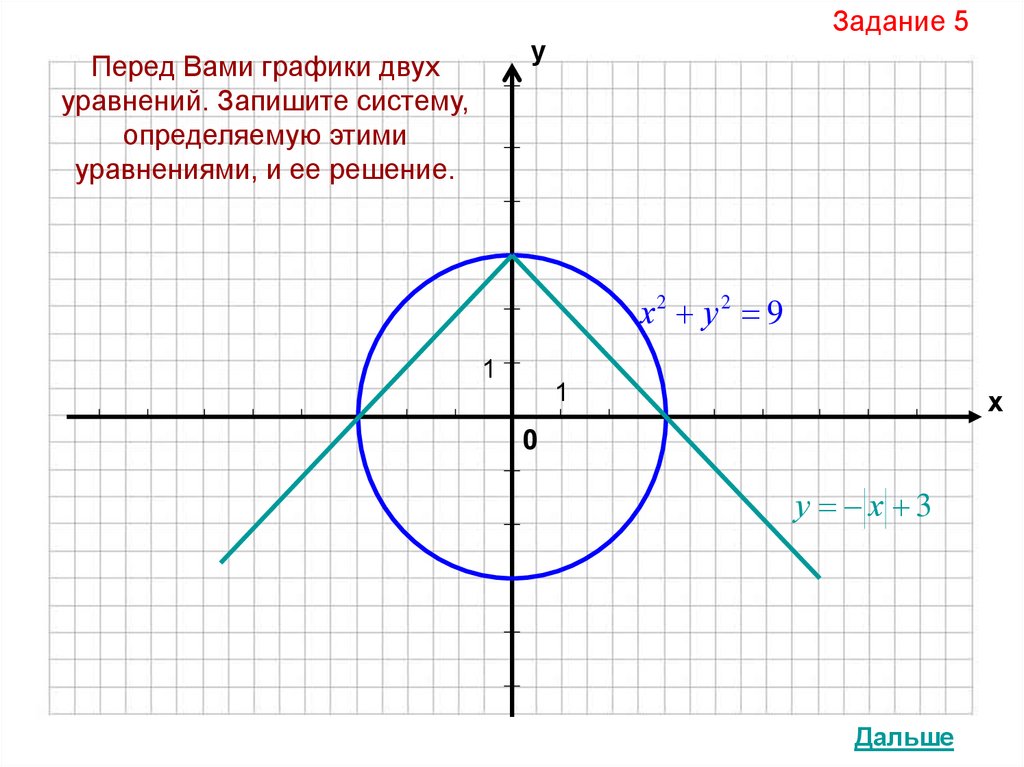
Задание 5у
Перед Вами графики двух
уравнений. Запишите систему,
определяемую этими
уравнениями, и ее решение.
х2 у2 9
1
1
х
0
у х 3
Дальше
21.
уЗадание 6
у х2 2
Перед Вами графики двух
уравнений. Запишите систему,
определяемую этими
уравнениями, и ее решение.
1
1
х
0
у х2 4
Дальше
22.
у0


















 Математика
Математика








