Функция. 9 класс

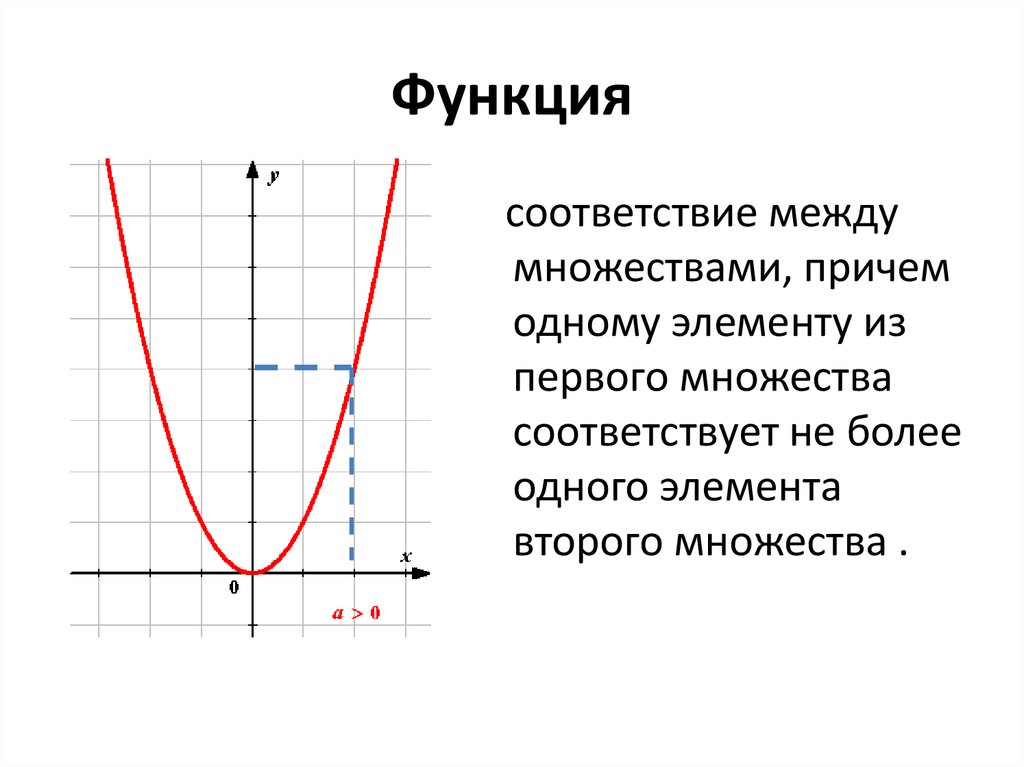
1. Функция

соответствие между
множествами, причем
одному элементу из
первого множества
соответствует не более
одного элемента
второго множества .

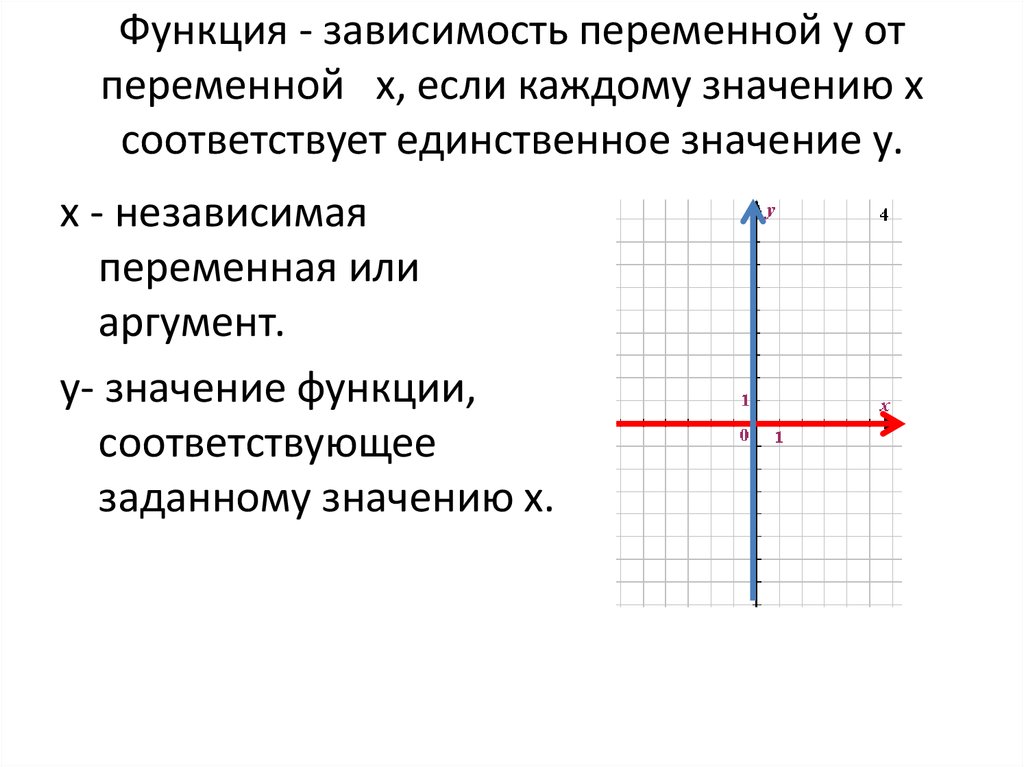
2. Функция - зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у.

х - независимая
переменная или
аргумент.
у- значение функции,
соответствующее
заданному значению х.

3.

первое множество
называется областью
определения функции
D ( f )= (-∞; +∞)
второе множество –
множеством значений
функции
E ( f )=[0; +∞).

4.

Область определения
функции - все значения,
которые принимает
независимая переменная.
D ( f )= (-∞; +∞)
Область значений функции
( множество значений )- все
значения, которые
принимает функция.
E ( f )=[0; +∞).

5. Виды функций

Линейная у 4 х 8
Прямая пропорциональность у 9,5 х
9
Обратная пропорциональность у
х
2
Квадратичная у х
Кубическая у 0,6 х 3 2
Квадратный корень у х
Модуль у I x I

6.

Какие из данных графиков
являются
Графиками функций?

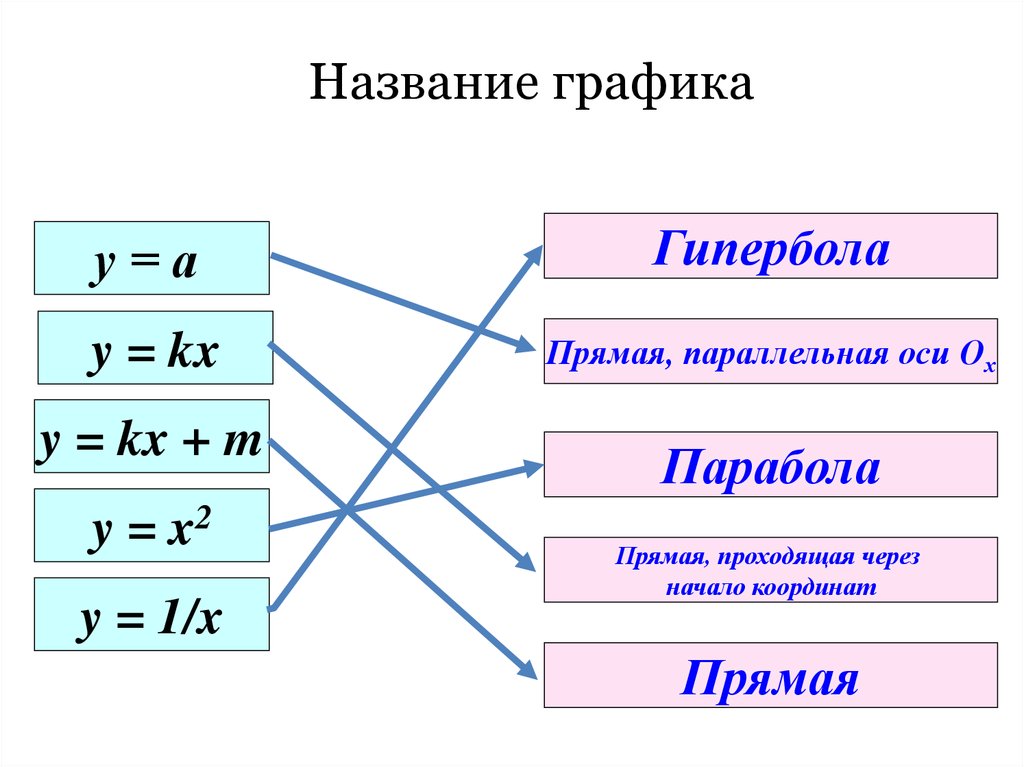
7.

Название графика
у=а
Гипербола
y = kx
Прямая, параллельная оси Ох
y = kx + m
y = x2
y = 1/x
Парабола
Прямая, проходящая через
начало координат
Прямая

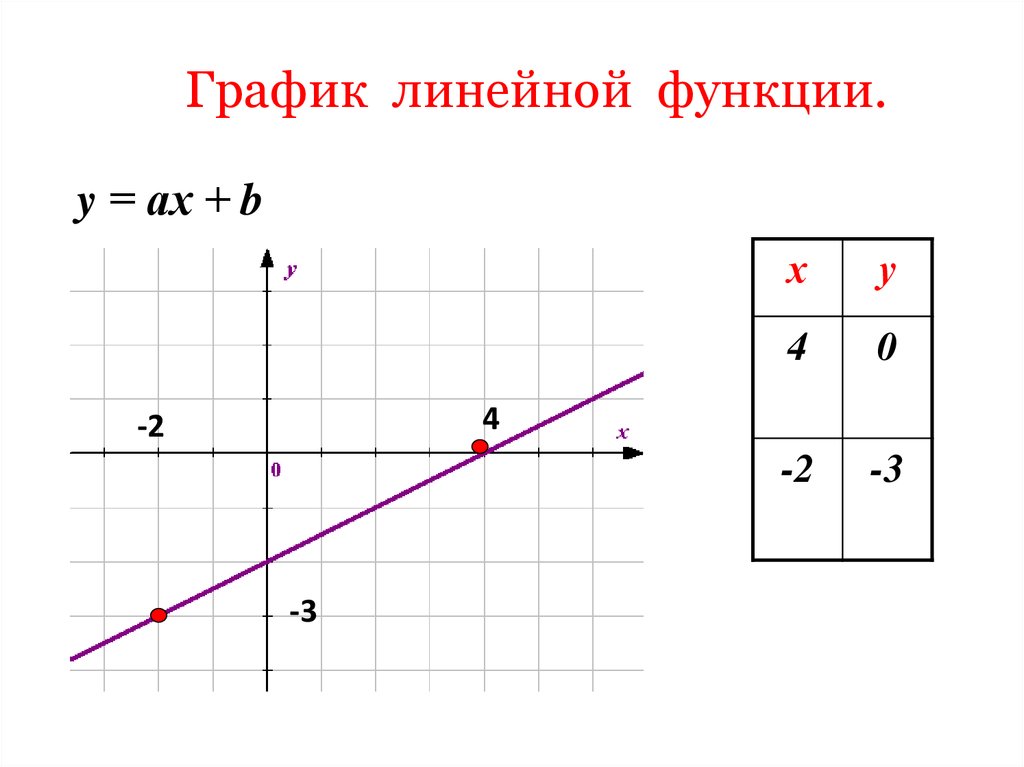
8. График линейной функции.

y = ах + b
х
у
4
0
-2
-3
4
-2
-3

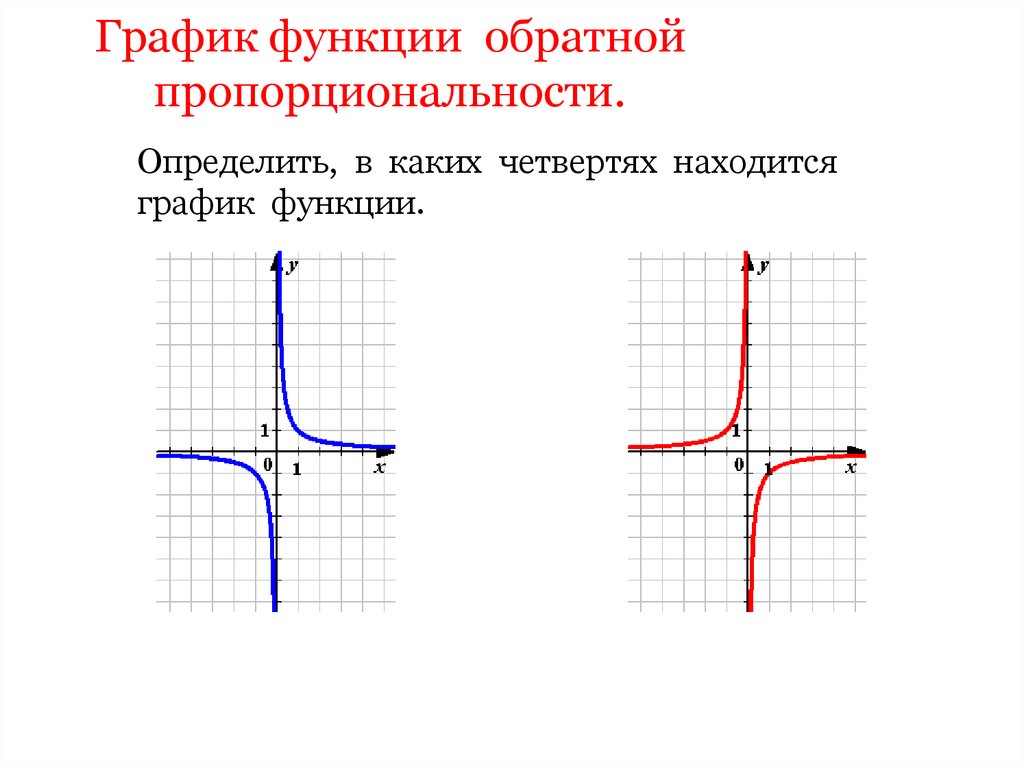
9. График функции обратной пропорциональности.

Определить, в каких четвертях находится
график функции.

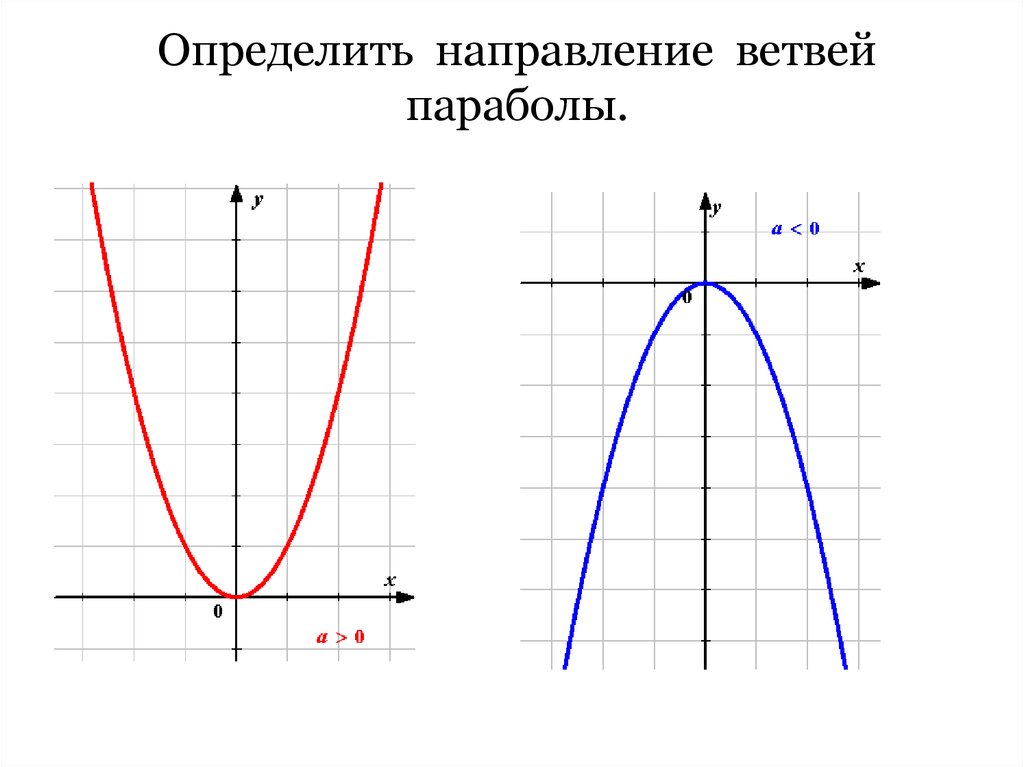
10. Определить направление ветвей параболы.

11. Преобразование графиков- найти

у 0,5 х
у х 2
у 3х 1
у 3

12.

Преобразование графиков- найти
1
1
1
1
у 2
у 2
у
у
х
х
х
х
1.
3.
2.
4.

13.

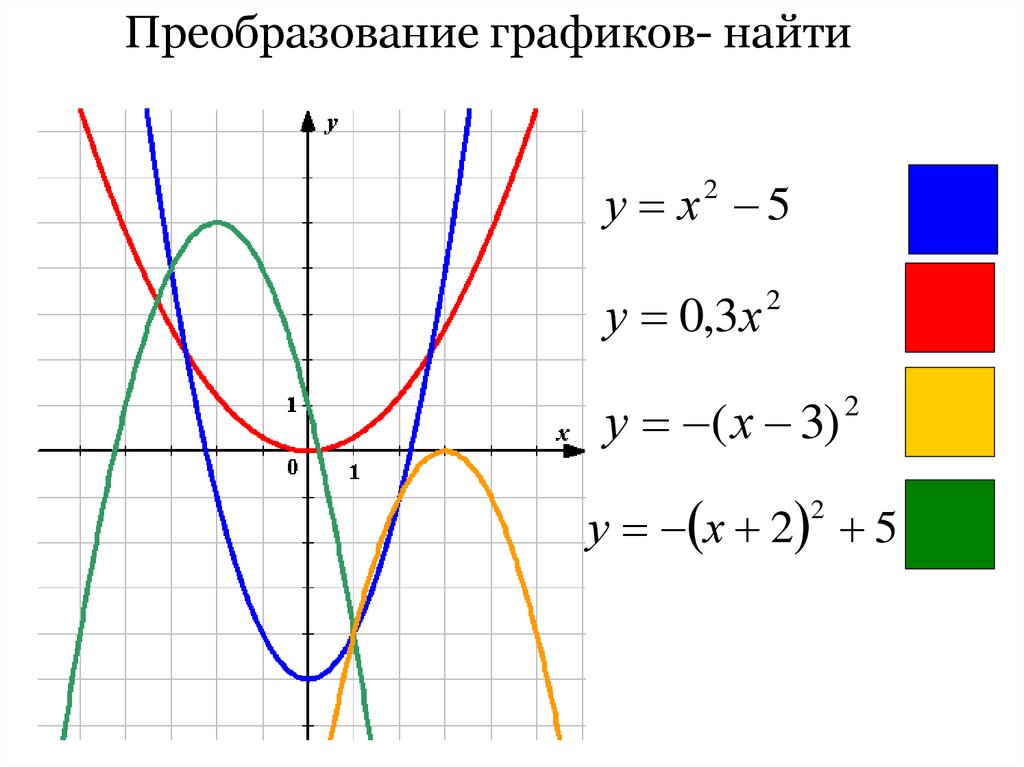
Преобразование графиков- найти
у х2 5
у 0,3х
2
у ( х 3)
2
у х 2 5
2

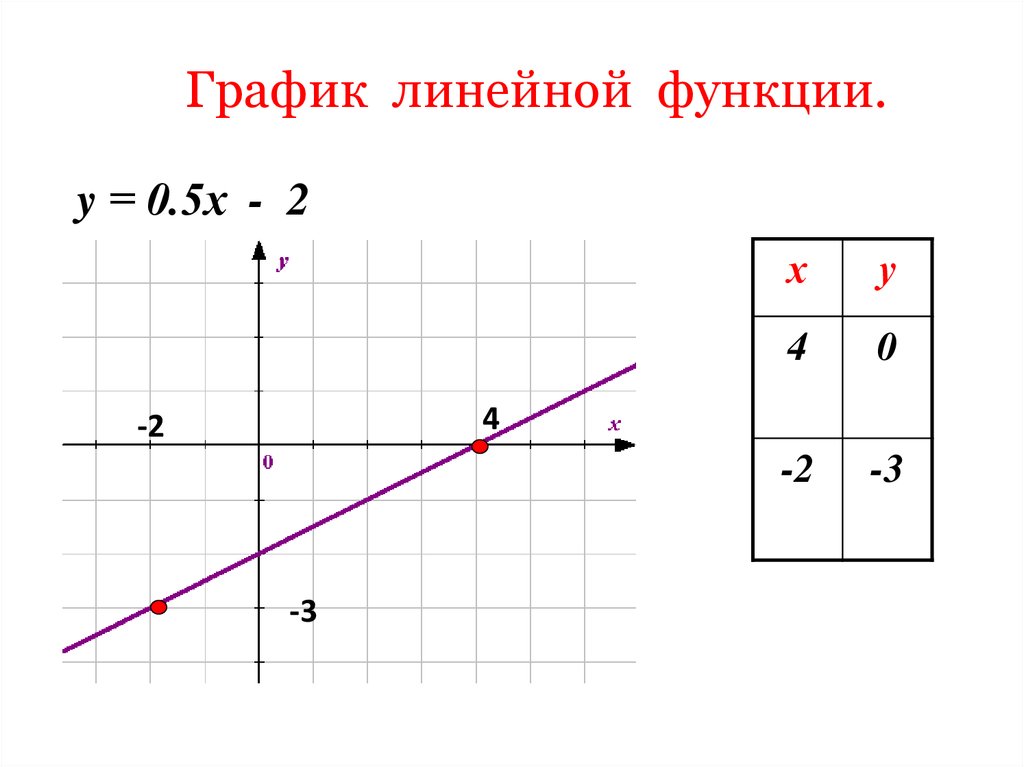
14. График линейной функции.

y = 0.5х - 2
х
у
4
0
-2
-3
4
-2
-3

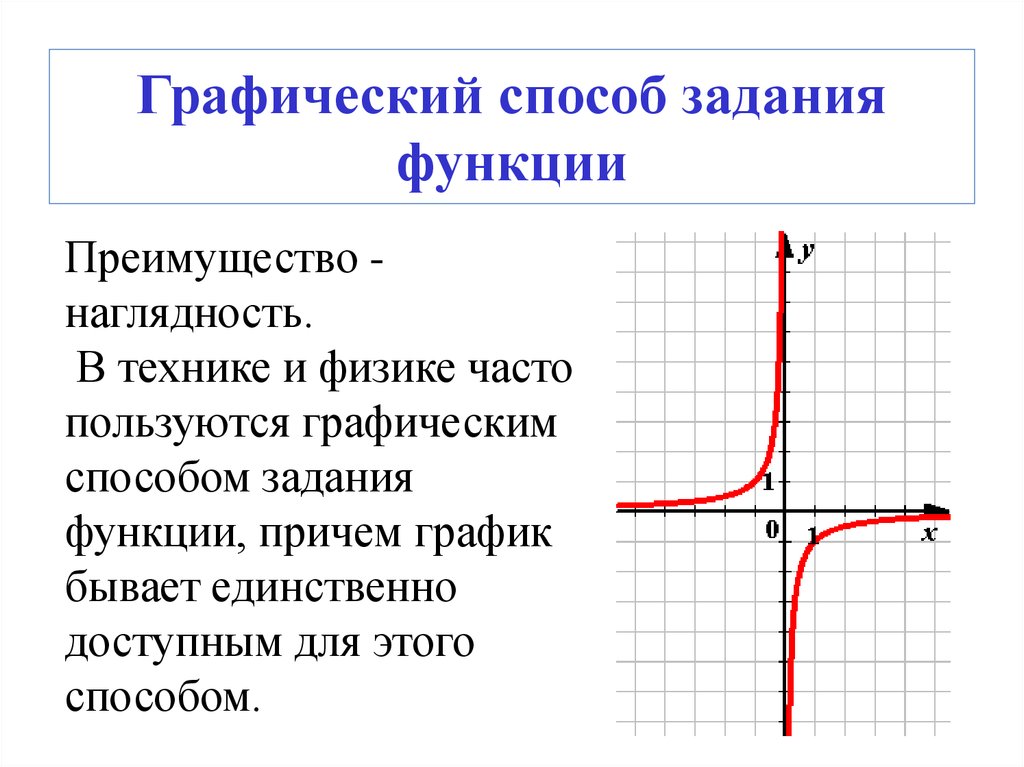
15. Графический способ задания функции

Преимущество наглядность.
В технике и физике часто
пользуются графическим
способом задания
функции, причем график
бывает единственно
доступным для этого
способом.

16.

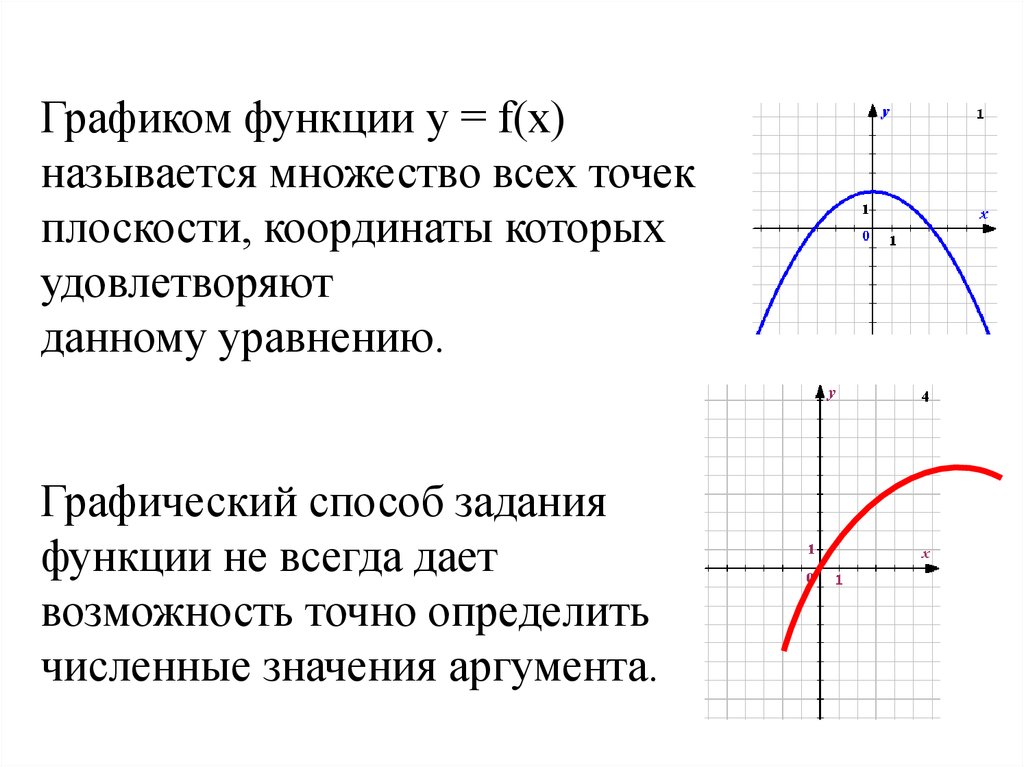
Графиком функции y = f(x)
называется множество всех точек
плоскости, координаты которых
удовлетворяют
данному уравнению.
Графический способ задания
функции не всегда дает
возможность точно определить
численные значения аргумента.

17. Аналитический способ

Самый распространенный
3
у 0,6 х 2
способом задания функций
- компактность
- возможность вычисления
значения функции при
произвольном значении аргумента
из области определения.

18. Недостатки

- отсутствие наглядности
(компенсируется возможностью
построения графика)
- необходимость выполнения
иногда очень громоздких
вычислений.

19. При аналитическом способе

функция может быть задана
явно
у 4 х 8
неявно
у 4х 8 0
параметрически
х=х(t) y=y (t)

20. Словесный способ задания функции Этот способ состоит в том, что функциональная зависимость выражается словами. функция E(x)

целая часть числа x.

21. Основными недостатками

- невозможность вычисления
значений функции при
произвольном значении
аргумента
- отсутствие наглядности

22. Главное преимущество

-возможность задания тех
функций, которые не удается
выразить аналитически.

23. Табличный способ

Функцию можно задать,
перечислив все её
возможные аргументы
и значения для них.
Примерами могут служить
программа передач, расписание
поездов
х
у
4
0
-2
-3

24. График роста 0 - 8 лет

х,л
0
1
2
3
у,м
0,5
0,8
0.95
1,0
4
5
6
7
8

25. Поход

х
0
1
2
у
0
4
8
2
1
4
у = 4х
8

26. Траектория полёта

У= а (х – в)² +с

27. Постоянное расстояние S=200км

U
50
100
200
25
t
4
2
1
8
У = 200 / х

28.

График
уравнения с
двумя
переменным
и

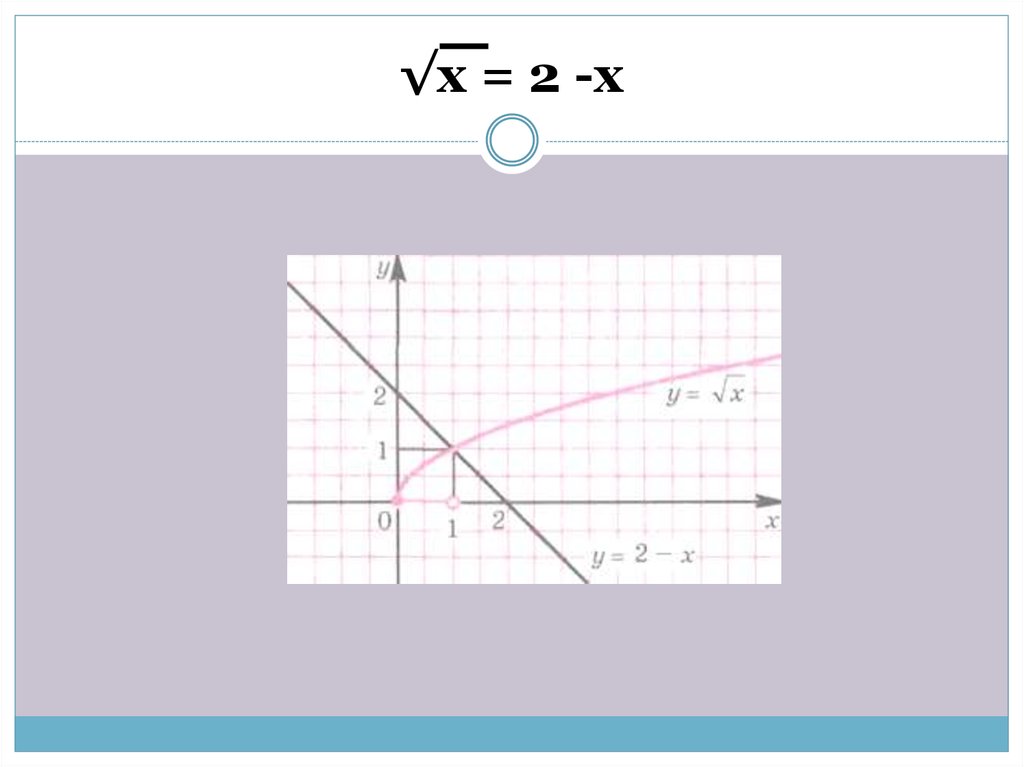
29. √x = 2 -x

30. √x < 2 -x

√x < 2 -x

31. √x+3 = x + 1

32. √x+3 > x + 1

√x+3 > x + 1

33. «…радость видеть и понимать…» А.Эйнштейн

Чувство Эмоции Разум
Возможность человеку
открывать