Похожие презентации:
Материалы к урокам и факультативным занятиям для 11 класса
1.
2. Материалы к урокам и факультативным занятиям для 11класса
Учитель ГБОУ гимназии № 49 Приморского района Санкт-ПетербургаАлексеевой Людмилы Васильевны
3.
«Если имеются две неравные площади,то, постоянно прибавляя к самому себе
избыток, на который большая площадь
превосходит меньшую, можно получить
площадь, которая была бы больше
любой заданной ограниченной площади.»
Архимед
4.
Определение.Криволинейной трапецией
называют фигуру,
ограниченную графиком
непрерывной функции,
заданной на отрезке [a;b] и
принимающей на нем
положительные значения,
отрезками прямых х=а и
х=b и отрезком [a;b] оси
абсцисс.
5.
Найти площадь криволинейнойтрапеции можно
способом последовательных приближений
способом составления интегральных сумм
используя определенный интеграл
6.
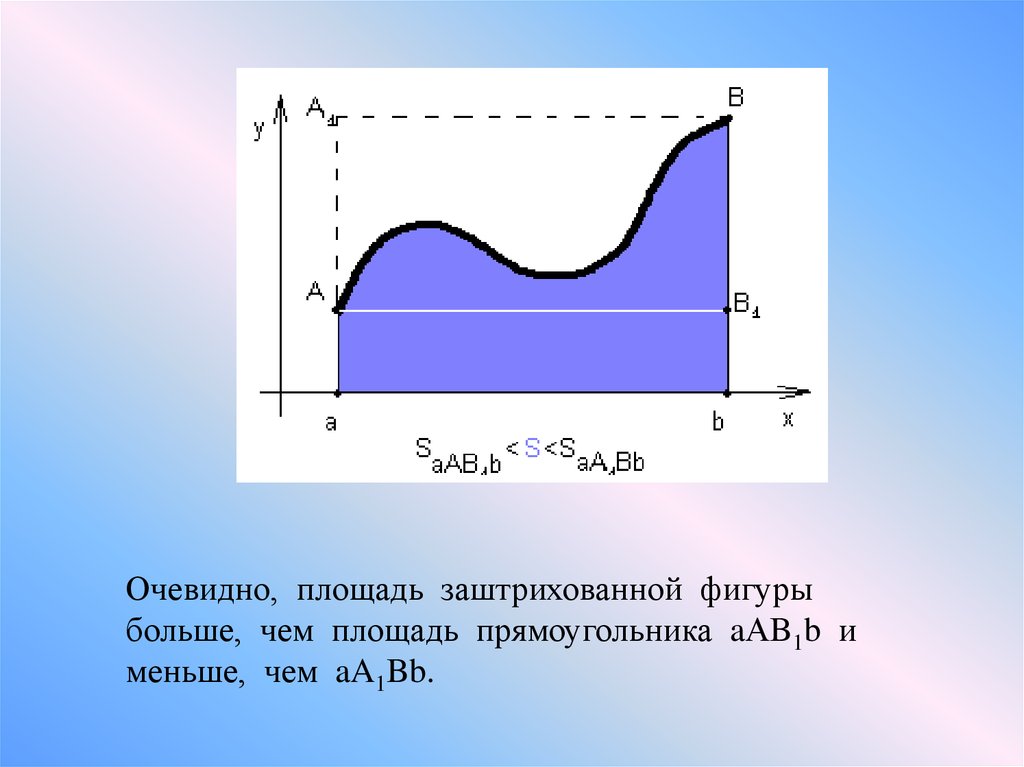
Очевидно, площадь заштрихованной фигурыбольше, чем площадь прямоугольника aАB1b и
меньше, чем aA1Bb.
7.
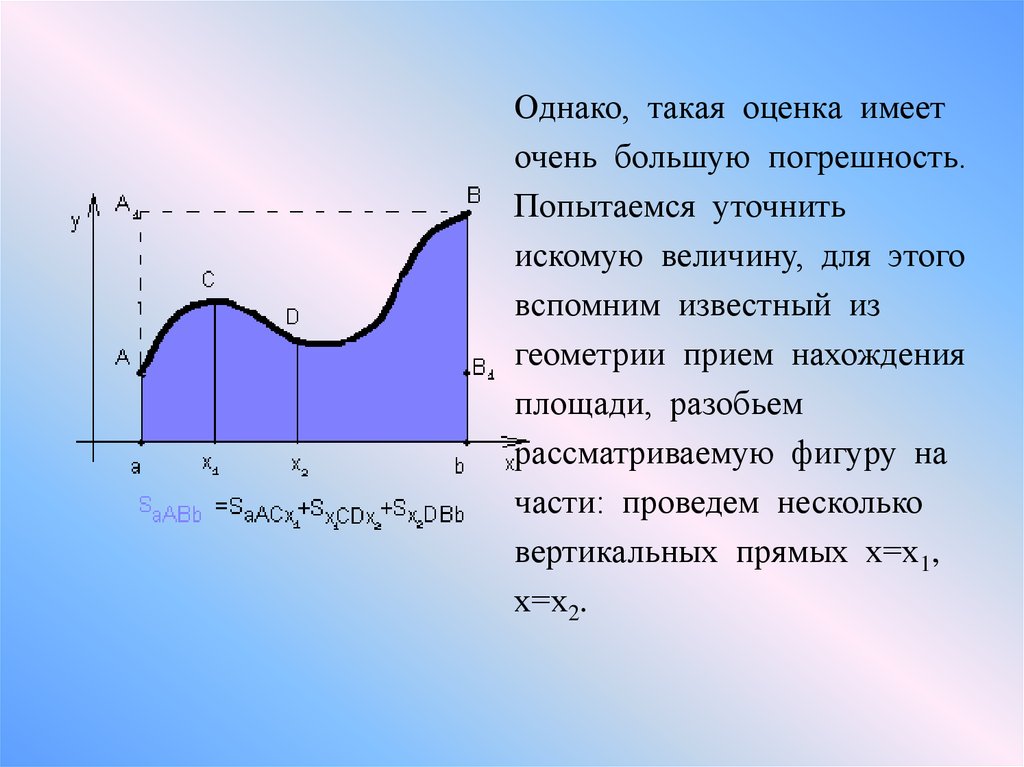
Однако, такая оценка имееточень большую погрешность.
Попытаемся уточнить
искомую величину, для этого
вспомним известный из
геометрии прием нахождения
площади, разобьем
рассматриваемую фигуру на
части: проведем несколько
вертикальных прямых х=х1,
х=х2.
8.
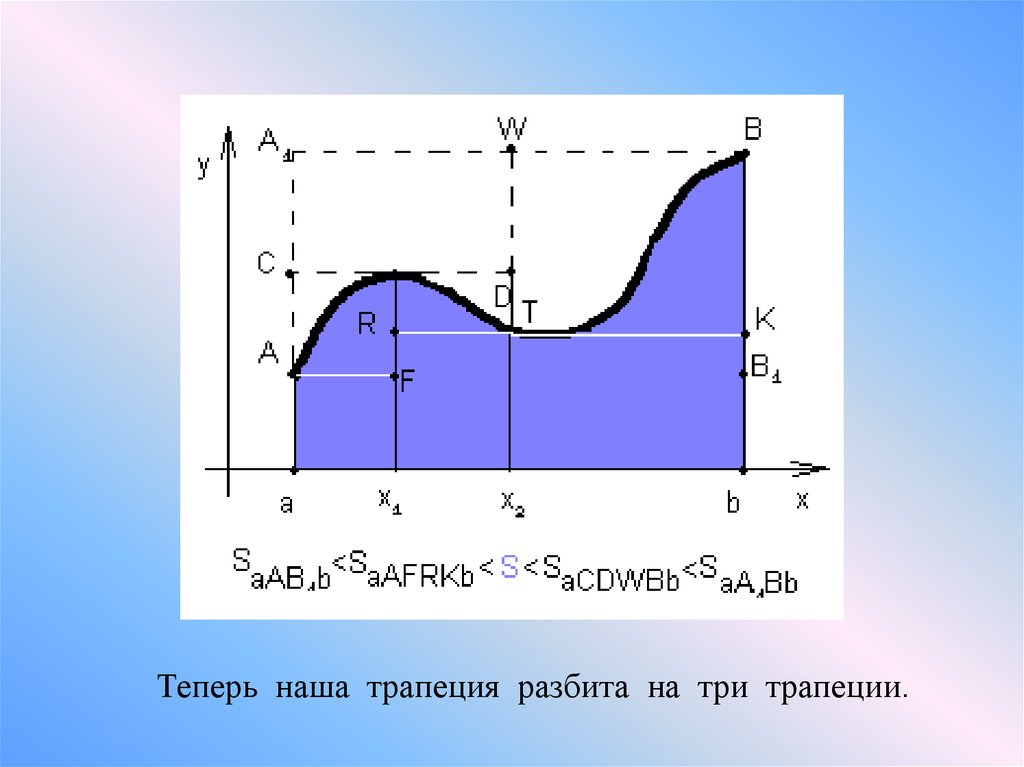
Теперь наша трапеция разбита на три трапеции.9.
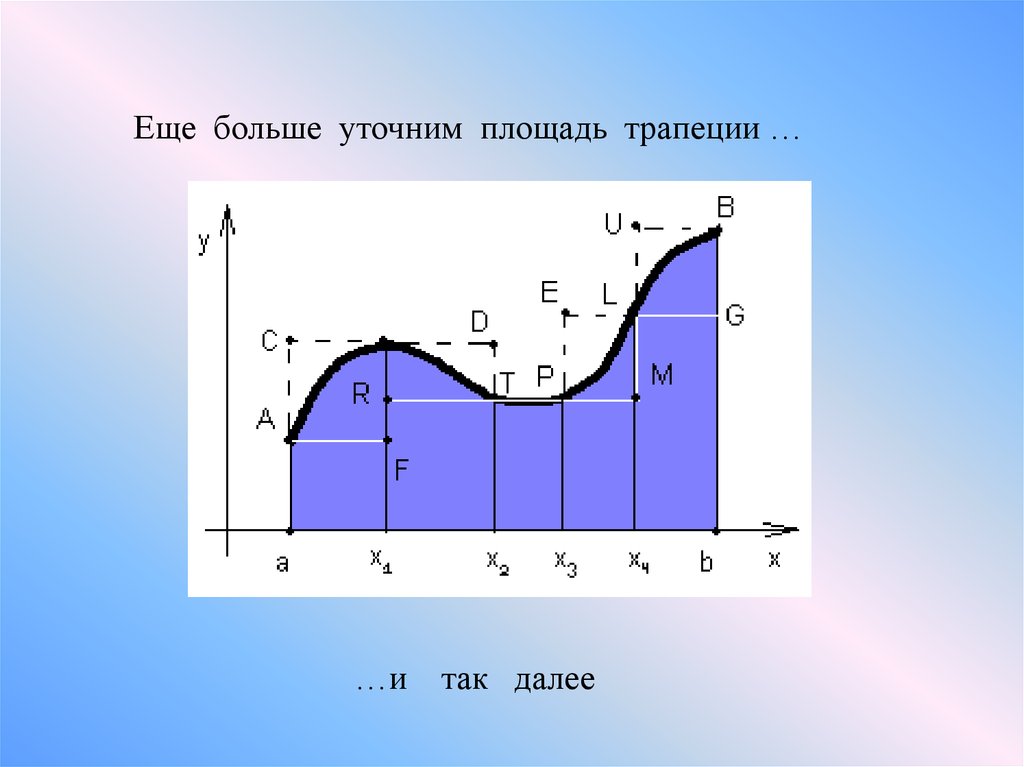
Еще больше уточним площадь трапеции ……и так далее
10.
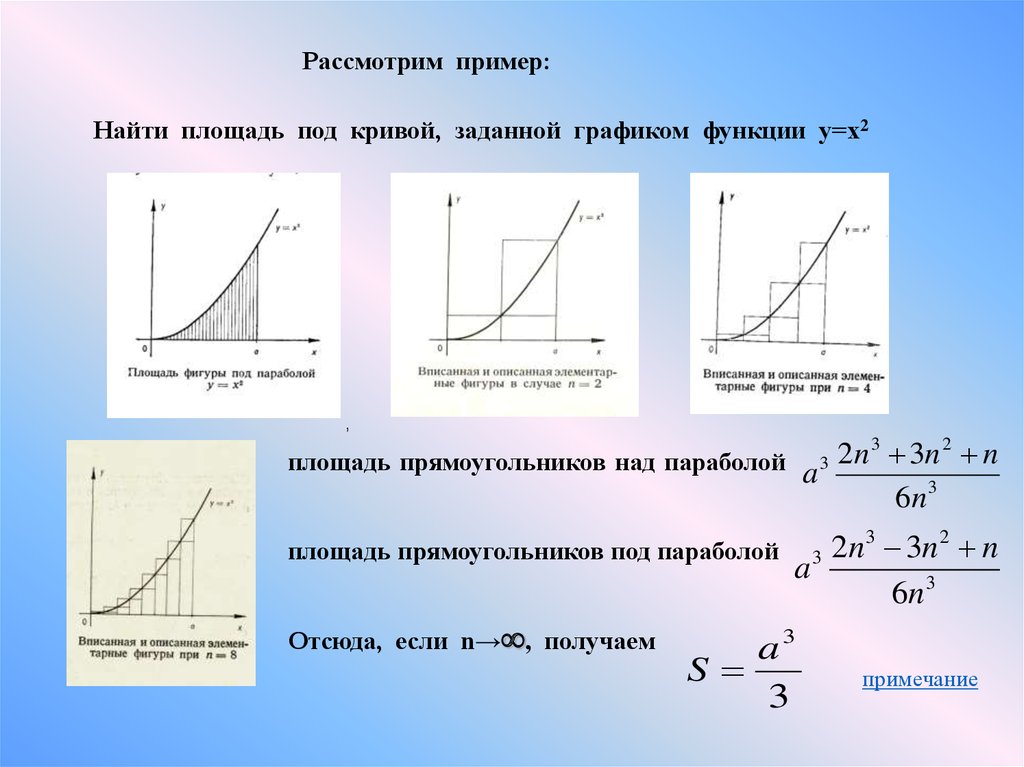
Рассмотрим пример:Найти площадь под кривой, заданной графиком функции у=х2
,
площадь прямоугольников над параболой a 3 2n 3n n
3
3
2
6n
площадь прямоугольников под параболой
Отсюда, если n→ , получаем
2n 3 3n 2 n
a
6n 3
a3
S
3
3
примечание
11.
Нахождение суммы последовательностиквадратов натуральных чисел
справедлива формула
n n 1 n 2
1 2 3 ... n
6
2
2
2
2
доказательство можно провести по индукции
12.
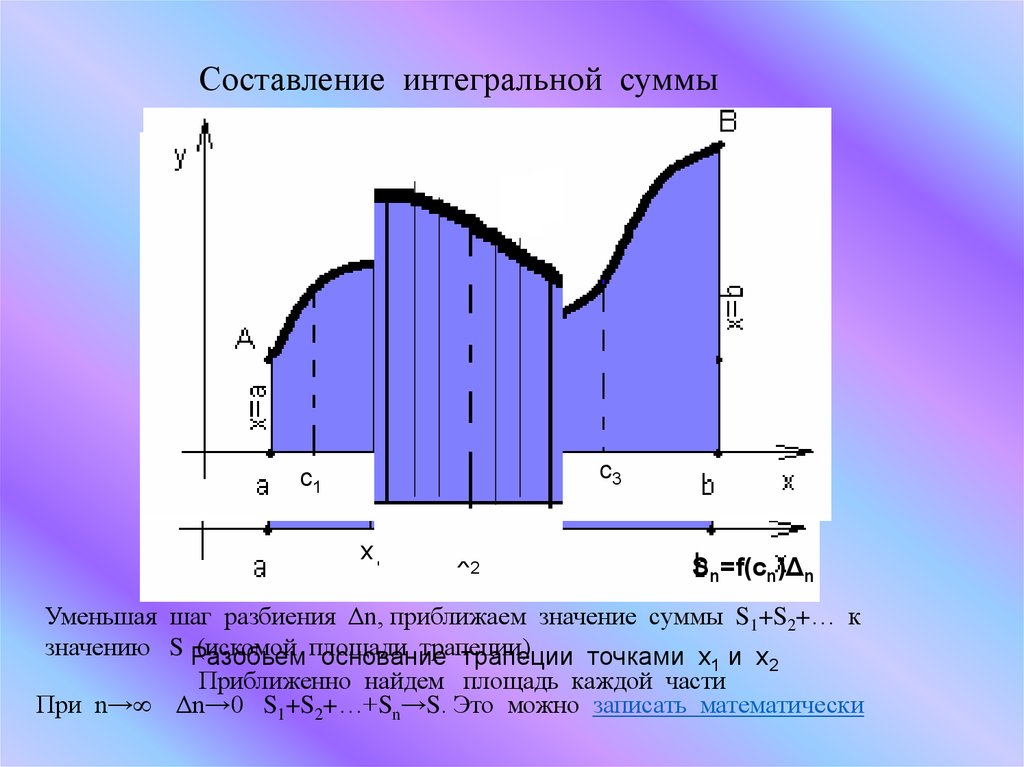
Составление интегральной суммыc1
c3
c2
х1
х2
Sn=f(cn)Δn
Уменьшая шаг разбиения Δn, приближаем значение суммы S1+S2+… к
значению S Разобьем
(искомой площади
трапеции)
основание
трапеции точками x1 и х2
Приближенно найдем площадь каждой части
При n→ Δn→0 S1+S2+…+Sn→S. Это можно записать математически
13.
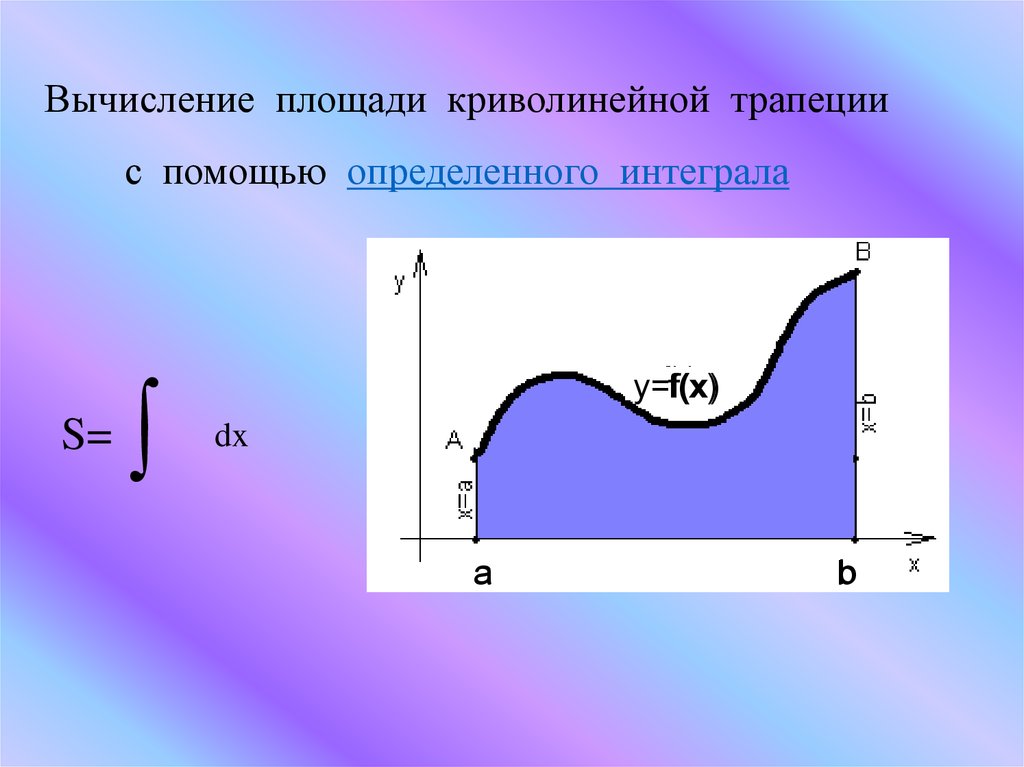
Вычисление площади криволинейной трапециис помощью определенного интеграла
S=
∫
y=f(x)
f(x)
dx
a
b
14.
Вычисление определенного интеграла.b
f
x
dx
F
b
F
a
a
Формула Ньютона – Лейбница
15.
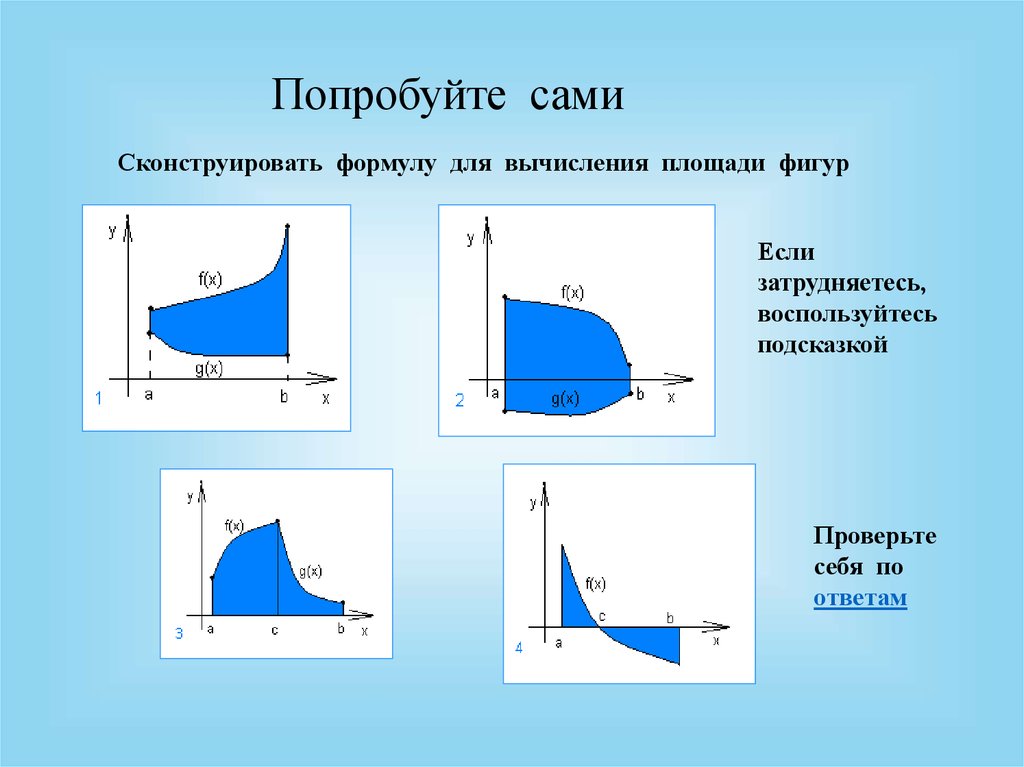
Попробуйте самиСконструировать формулу для вычисления площади фигур
Если
затрудняетесь,
воспользуйтесь
подсказкой
Проверьте
себя по
ответам
16.
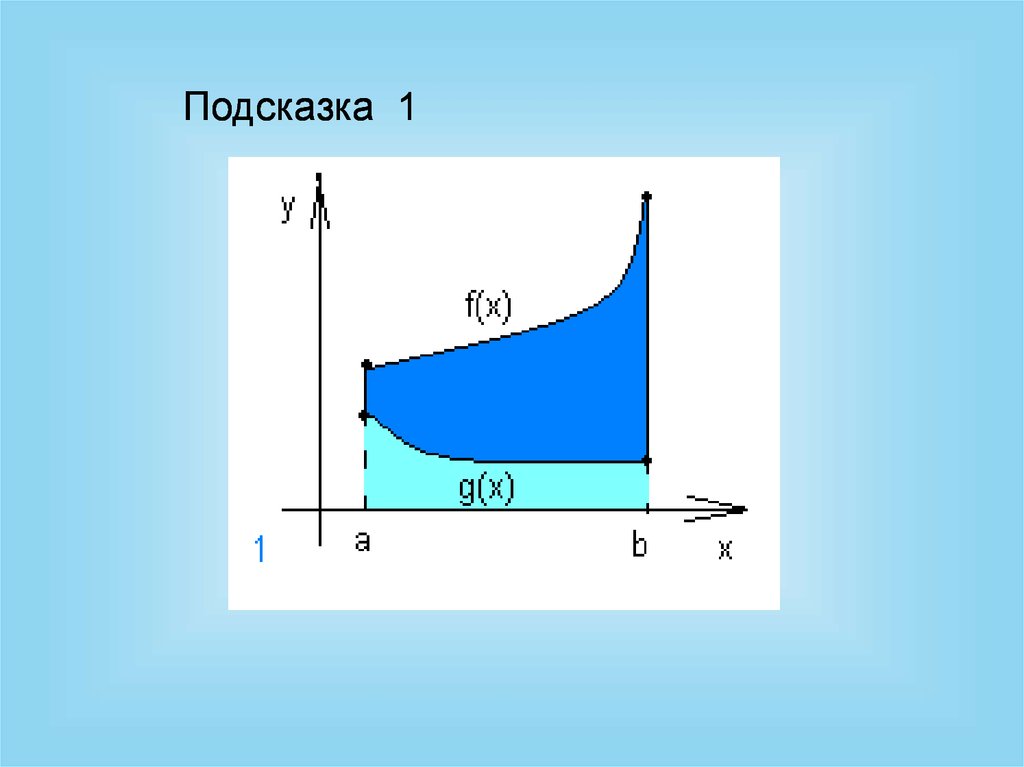
Подсказка 117.
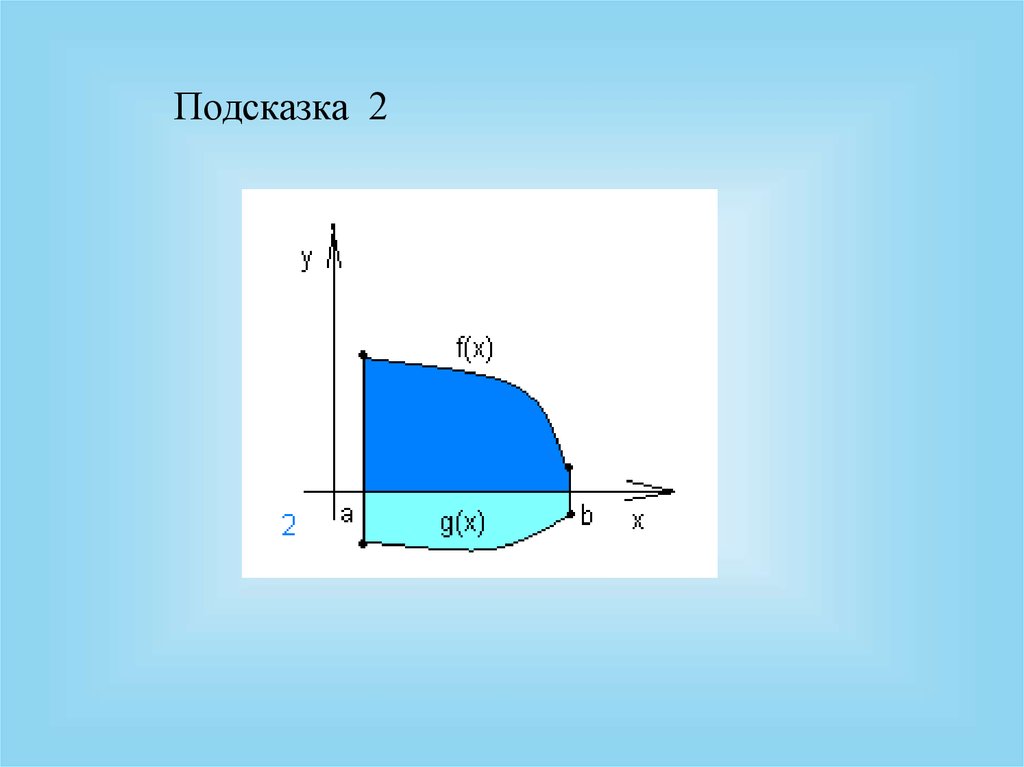
Подсказка 218.
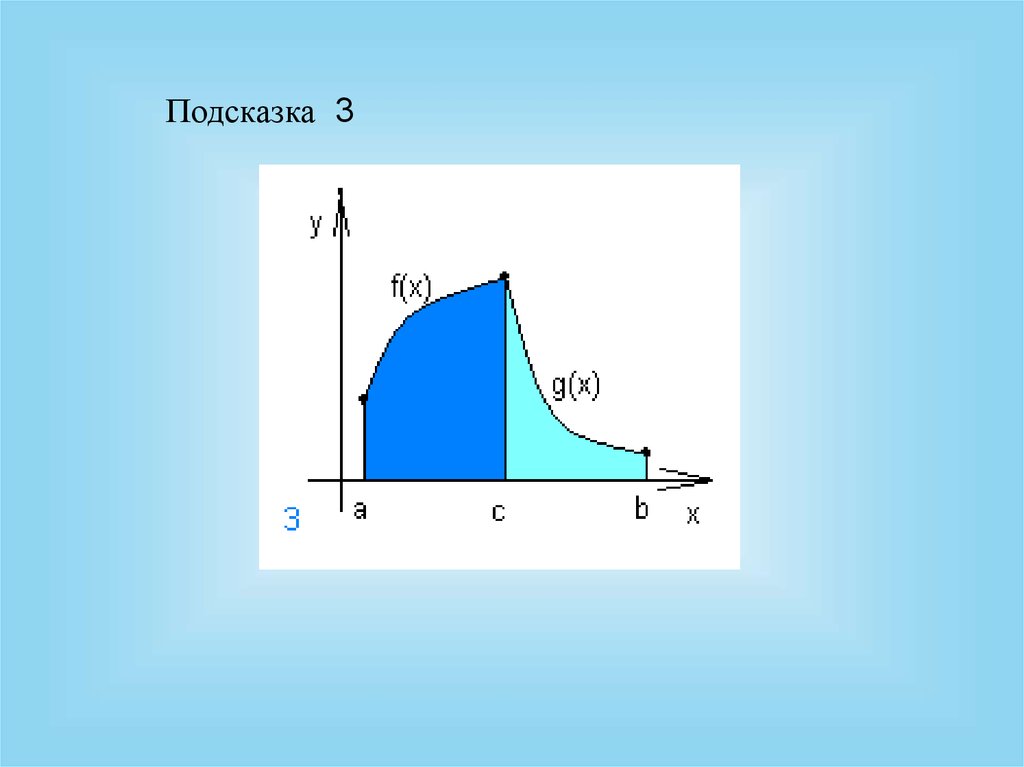
Подсказка 319.
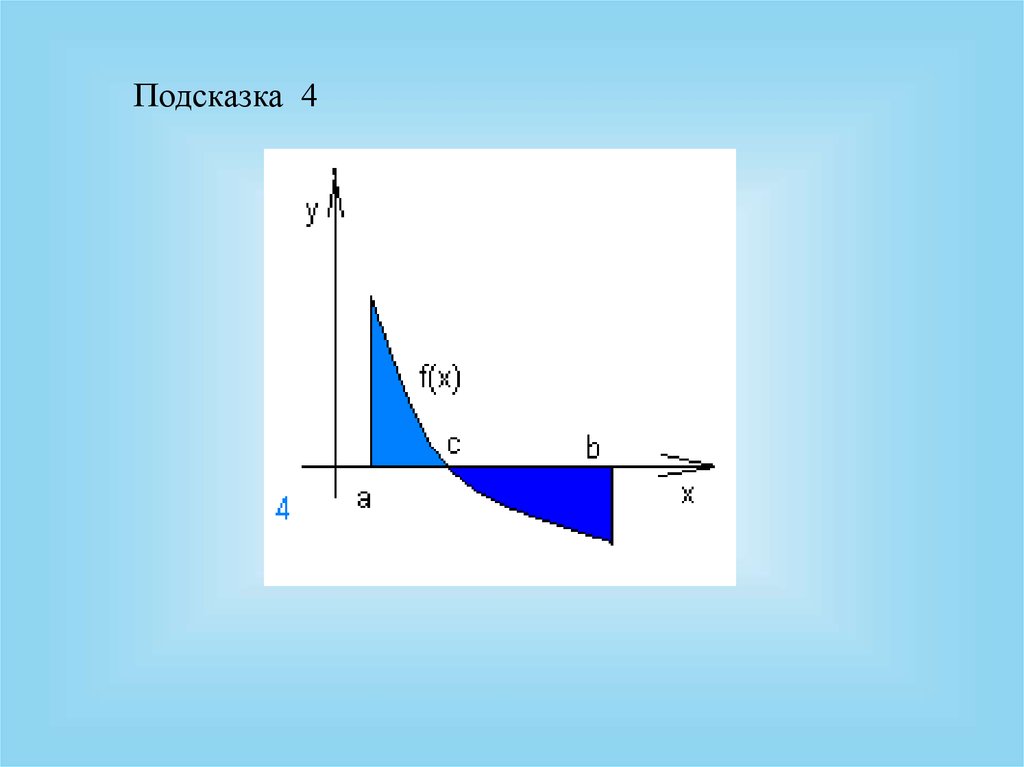
Подсказка 420.
Проверь себя1.
b
b
b
a
a
a
S f x dx g x dx f x g x dx
b
2. S
f x g x dx
a
b
4. S
f x dx
a
3.
b
b
a
a
S f x dx g x dx
Ура! Получилось!
М о л о д е ц !!!








 Математика
Математика Педагогика
Педагогика








