Прямоугольный параллелепипед

1.

2.

ПРЯМОУГОЛЬНЫЙ
ПАРАЛЛЕЛЕПИПЕД
Параллелепипед называется прямоугольным, если его боковые рёбра перпендикулярны к основанию, а основания являются прямоугольниками.

3.

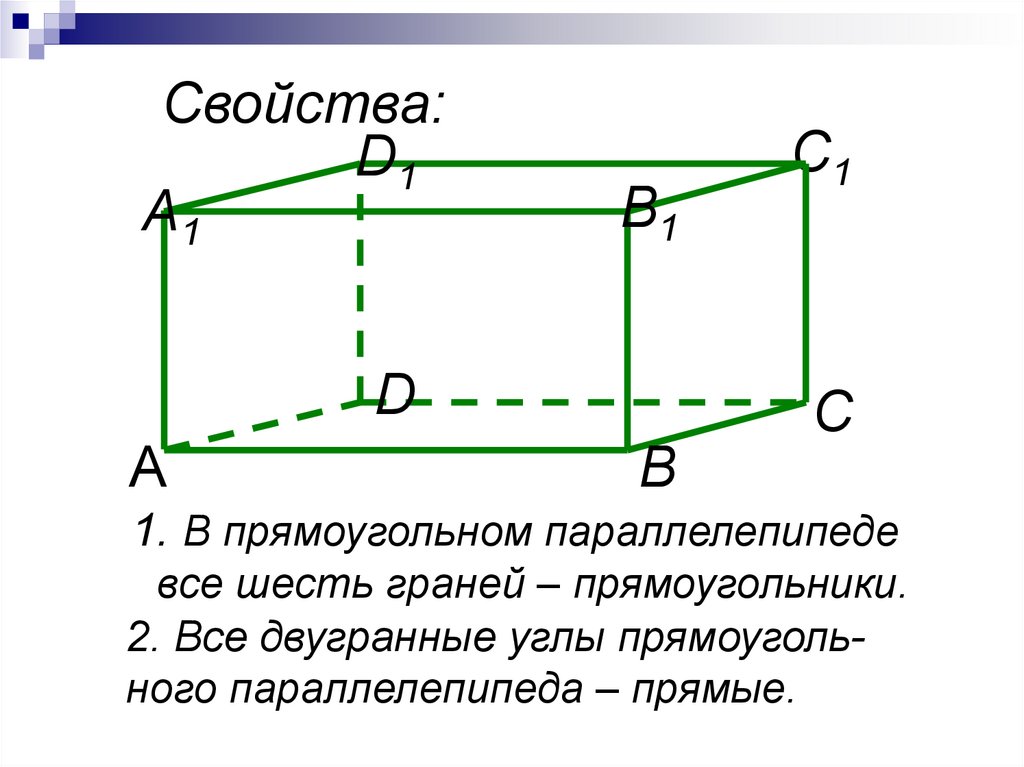
Свойства:
D1
A1
B1
D
А
В
C1
С
1. В прямоугольном параллелепипеде
все шесть граней – прямоугольники.
2. Все двугранные углы прямоугольного параллелепипеда – прямые.

4.

Теорема: квадрат диагонали
прямоугольного
параллелепипеда равен сумме
квадратов трех его измерений

5.

C1 Доказать:
D1
AC1 2=AB2+AD2+AA12
B1
A1
Доказательство:
1. ABD –
прямоугольный
По т. Пифагора
DB2=AB2+AD2
D
А
С
В
2. BDD1 –
прямоугольный
По т. Пифагора
BD12=BD2+DD12
3. Из 1 и 2 следует: AC1 2=AB2+AD2+AA12

6.

СЛЕДСТВИЕ:
ДИАГОНАЛИ ПРЯМОУГОЛЬНОГО
ПАРАЛЛЕЛЕПИПЕДА РАВНЫ

7.

Формулы полной поверхности и объёма
прямоугольного параллелепипеда
Sпов. 2(ab bc ac)
V a b c
c
d
b
a (а=в=с - куб)
V S осн h
Sпов. Sбок. 2Sосн.
Sбок. Pосн.h

8.

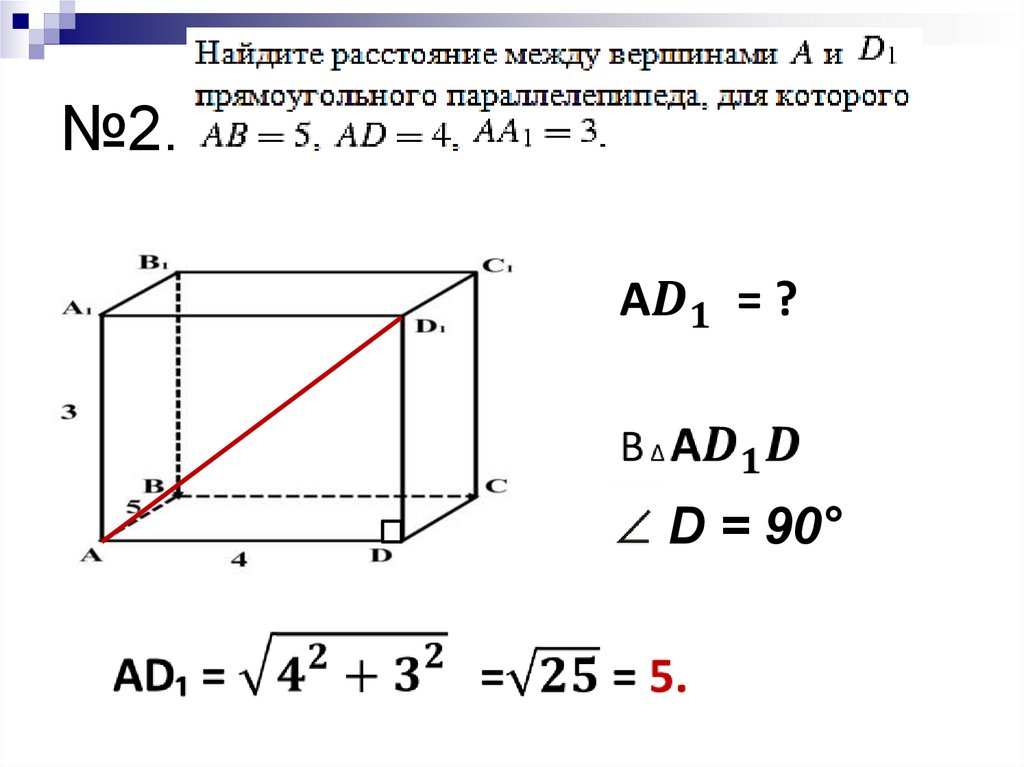
ЗАДАЧИ НА ЕГЭ

9. №1.

16+25+9 = 50.

10. №2.

D = 90°

11. №3.

3
45°
5 3
D= 90° ;
4 45°
5
A = 90° ;
B = 45°;

12.

№ 4.
Объем куба равен 64.
Найдите площадь его поверхности.
V a
a
a2
a
a
S 6a
3
2
V 64
S 6 4
a 64
S 96
3
a 3 64
a 4
9 6
3
10 х
х
2

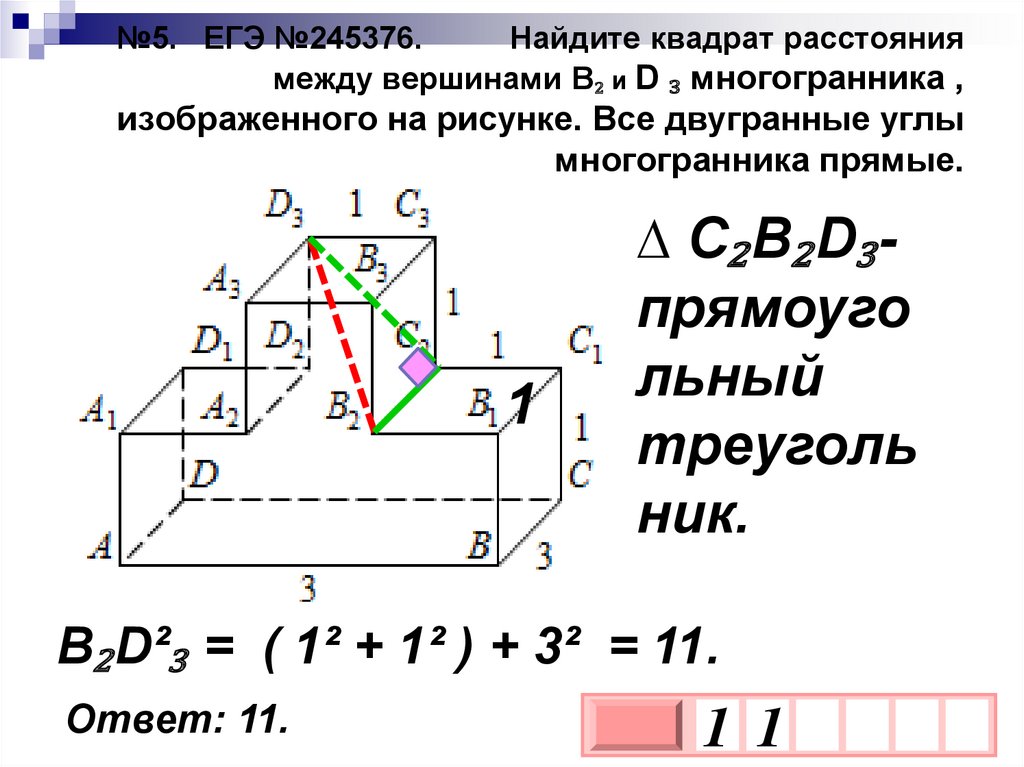
13. №5. ЕГЭ №245376. Найдите квадрат расстояния между вершинами B₂ и D ₃ многогранника , изображенного на рисунке. Все двугранные

углы
многогранника прямые.
1
∆ C₂B₂D₃прямоуго
льный
треуголь
ник.
B₂D²₃ = ( 1² + 1² ) + 3² = 11.
Ответ: 11.
1 1
3
10 х
х

14. № 6. ЕГЭ №245373. Найдите угол CAD₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ

дайте в градусах.
AD₂ = CD₂= CA- диагонали
равных квадратов .
∆ CAD₂ - равносторонний
треугольник.
CAD₂=60°.
60°
Ответ:60°.
6 0
3
10 х
х

15.

№ 7. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
4
3
2
8
Площадь поверхности данной фигуры
будет равна площади поверхности
прямоугольного параллелепипеда.
Sпп 2(8 10 8 6 6 10) 376
6
10
3 7 6
3
10 х
х

16.

№8. Найдите объём многогранника, изображенного на
рисунке (все двугранные углы прямые).
V1 8 10 6 480
4
3
2
8
6
{8;6;10}
V2 2 3 4 24
{2;3;4}
10
V V1 V2 480 24 456
4 5 6
3
10 х
х

17.

№9. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
4
2
S1 2 (3 2 2 4 4 3) 52
3
6
S2 2 (3 5 5 4 4 3) 94
3
4
5
S3 2 4 8
S S1 S 2 2 S3 52 94 2 8 130
1 3 0
3
10 х
х

18.

№10. Найдите объём многогранника, изображенного на рисунке
(все двугранные углы прямые).
4
2
V1 3 2 4 24
3
6
V2 3 5 4 60
3
4
5
V V1 V2 24 60 84
8 4
3
10 х
х

19. Домашнее задание

Стр. 53 – 54 повт
п.19-24
Б-№ 187(б),
190(а,б), п-193(а,б)