Треугольники

1. Треугольники

Виды треугольников
Элементы треугольника
Свойства
Равенство треугольников
Подобие треугольников
Формулы площади

2.

А,В,С – вершины
В
АВС.
АВ,ВС,АС – стороны
АВС.
АС ВС АВ АС ВС
Стороны любого треугольника подчинены
условию:длина каждой из них меньше
суммы и больше разности длин двух других
сторон.
Сумма углов треугольника равна 180
А
С

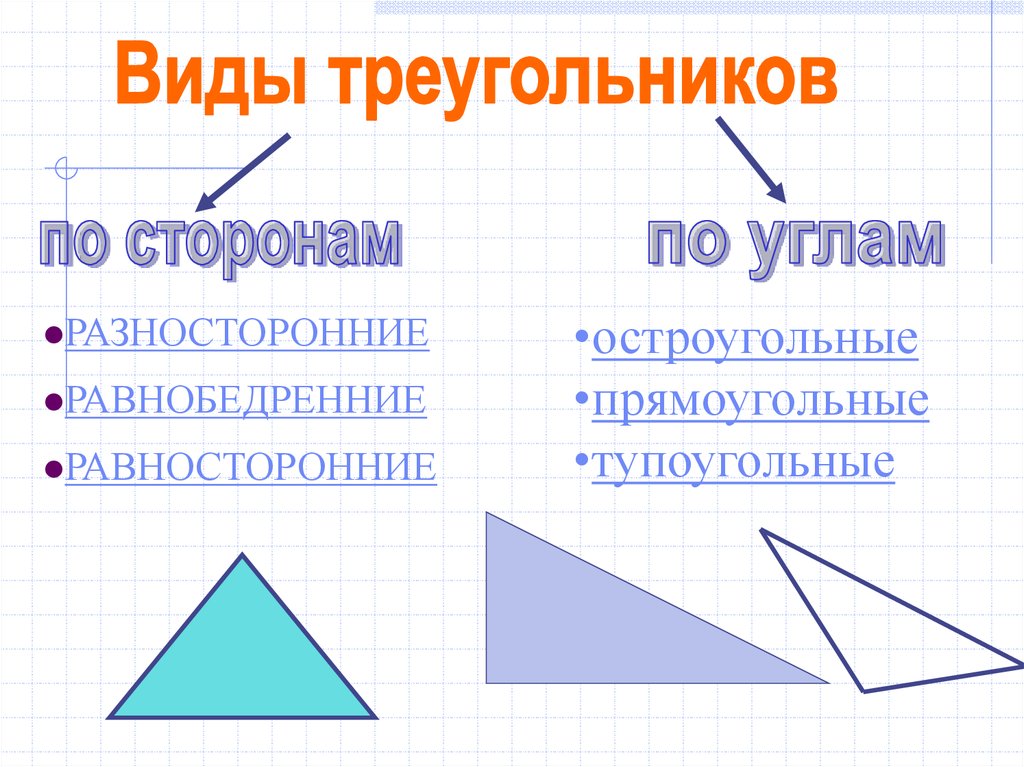
3.

РАЗНОСТОРОННИЕ
РАВНОБЕДРЕННИЕ
РАВНОСТОРОННИЕ
•остроугольные
•прямоугольные
•тупоугольные

4.

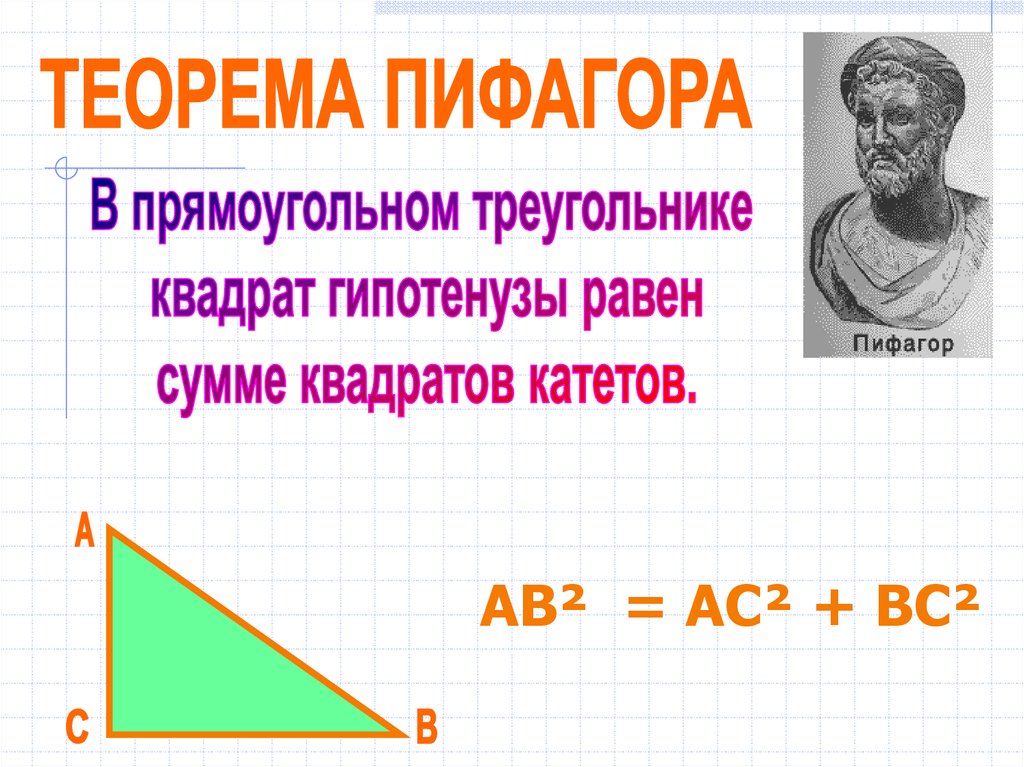
5.

AB² = AC² + BC²

6.

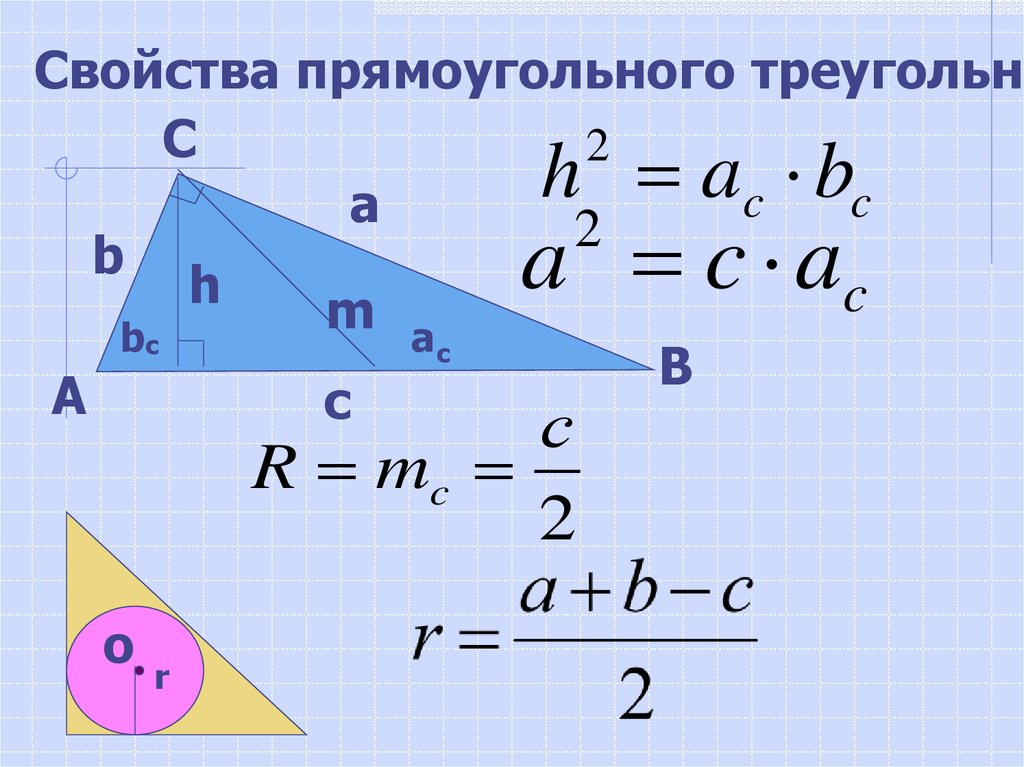
Свойства прямоугольного треугольни
С
2
h
a
b
c
c
а
2
b
h
c
m
bc
ac
В
А
c
a c a
с
R mc
2
o
r

7.

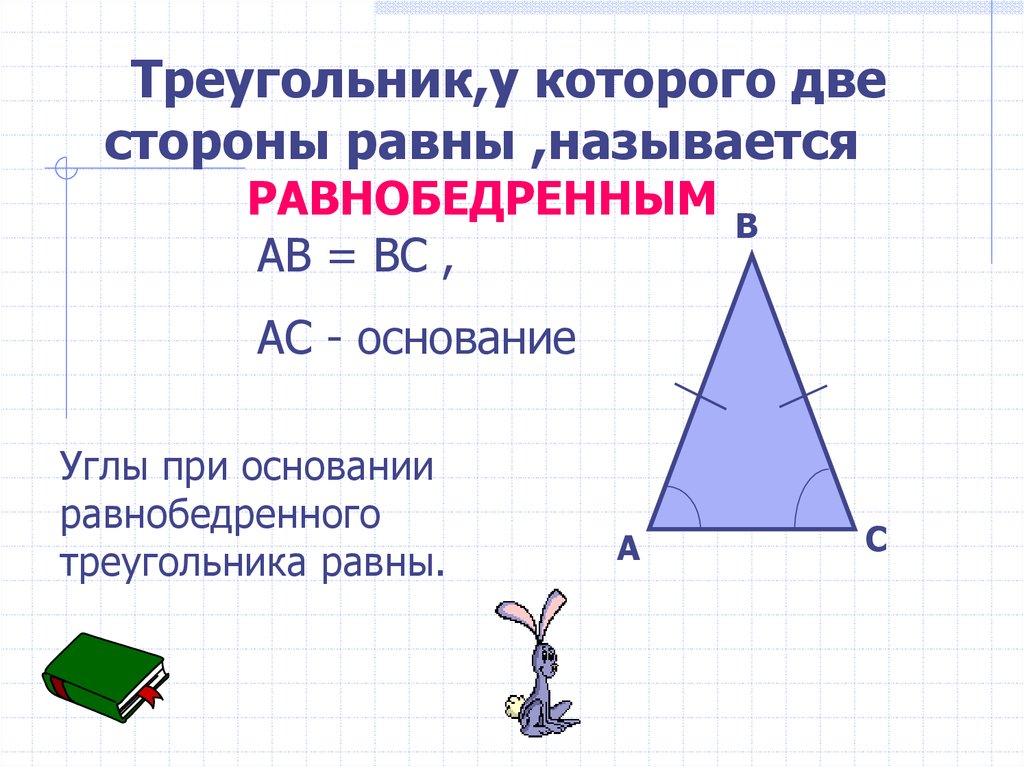
Треугольник,у которого две
стороны равны ,называется
РАВНОБЕДРЕННЫМ
AB = BC ,
В
AC - основание
Углы при основании
равнобедренного
треугольника равны.
А
С

8.

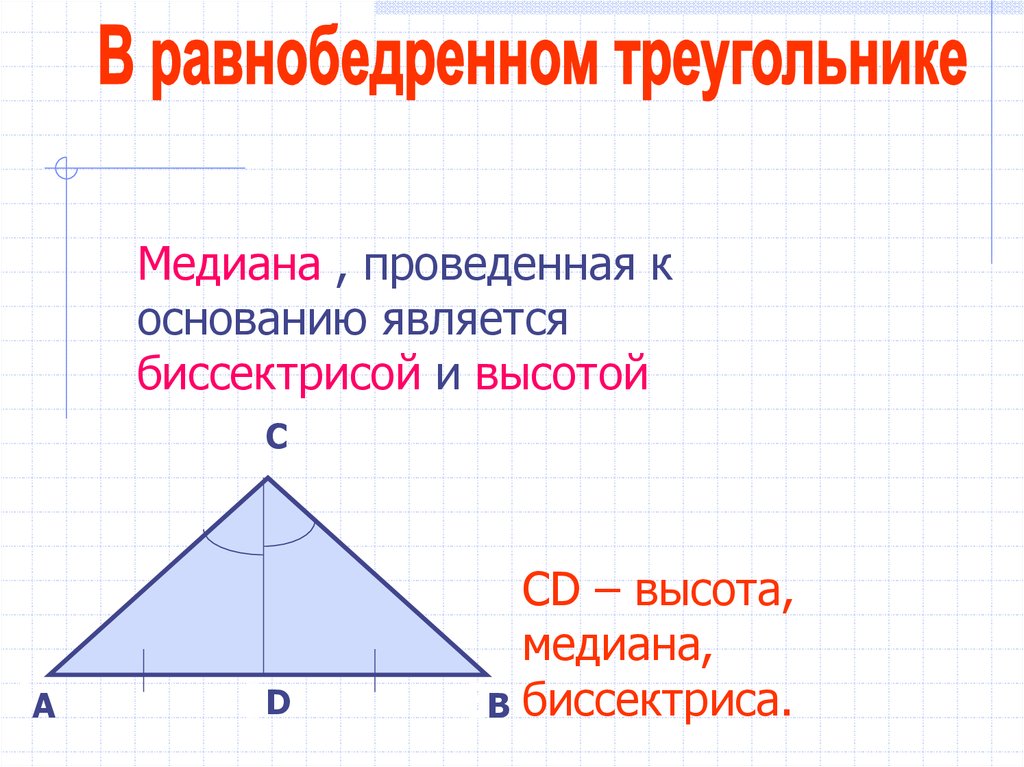
Медиана , проведенная к
основанию является
биссектрисой и высотой
С
A
D
CD – высота,
медиана,
B биссектриса.

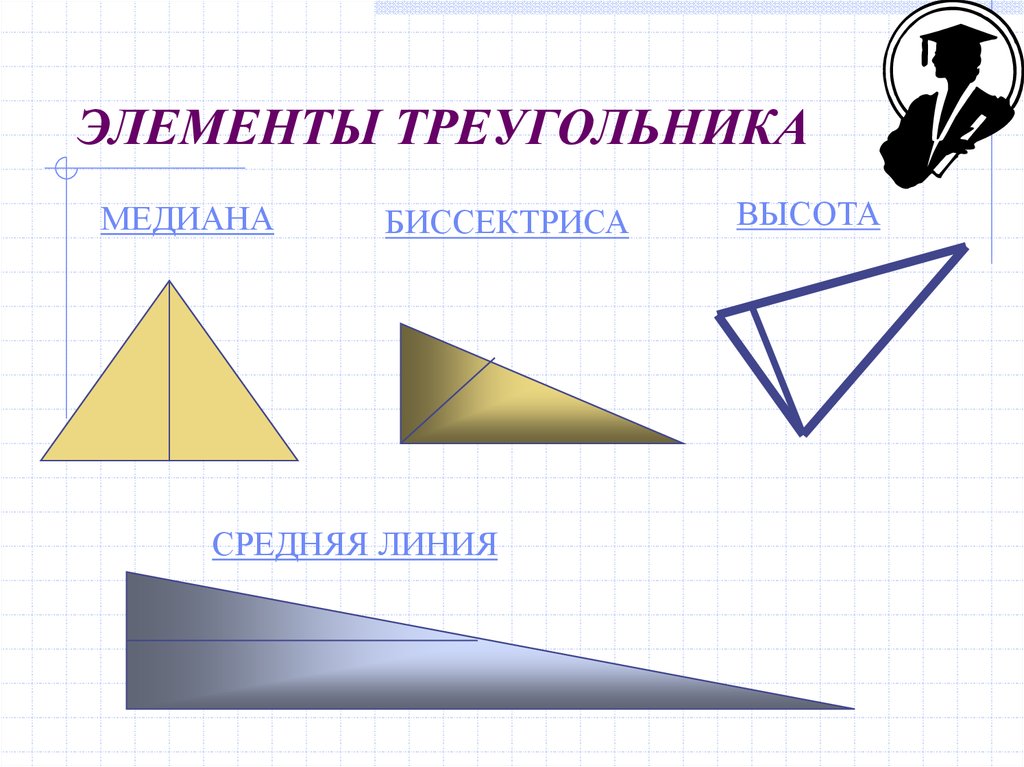
9. ЭЛЕМЕНТЫ ТРЕУГОЛЬНИКА

МЕДИАНА
БИССЕКТРИСА
СРЕДНЯЯ ЛИНИЯ
ВЫСОТА

10. СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА

СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА-ОТРЕЗОК,
КОТОРЫЙ СОЕДИНЯЕТ СЕРЕДИНЫ ДВУХ СТОРОН
ЭТОГО ТРЕУГОЛЬНИКА.
В
Д-СЕРЕДИНА АВ
Е-СЕРЕДИНА АС
Д
А
ДЕ-СРЕДНЯЯ
ЛИНИЯ
СВОЙСТВА
Е
С
1.СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА ПАРАЛЛЕЛЬНА ОСНОВАНИЮ ТРЕУГОЛЬНИКА;
2.СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА РАВНА ПОЛОВИНЕ ОСНОВАНИЯ ТРЕУГОЛЬНИКА;

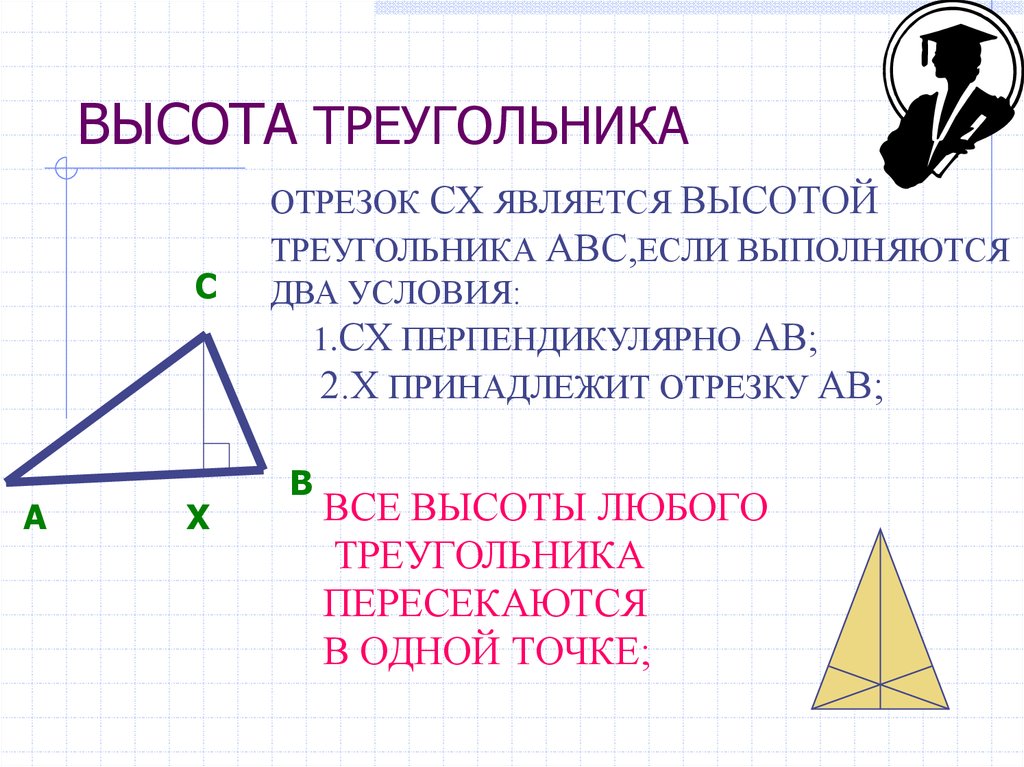
11. ВЫСОТА ТРЕУГОЛЬНИКА

С
А
Х
ОТРЕЗОК СХ ЯВЛЯЕТСЯ ВЫСОТОЙ
ТРЕУГОЛЬНИКА АВС,ЕСЛИ ВЫПОЛНЯЮТСЯ
ДВА УСЛОВИЯ:
1.СХ ПЕРПЕНДИКУЛЯРНО АВ;
2.Х ПРИНАДЛЕЖИТ ОТРЕЗКУ АВ;
В
ВСЕ ВЫСОТЫ ЛЮБОГО
ТРЕУГОЛЬНИКА
ПЕРЕСЕКАЮТСЯ
В ОДНОЙ ТОЧКЕ;

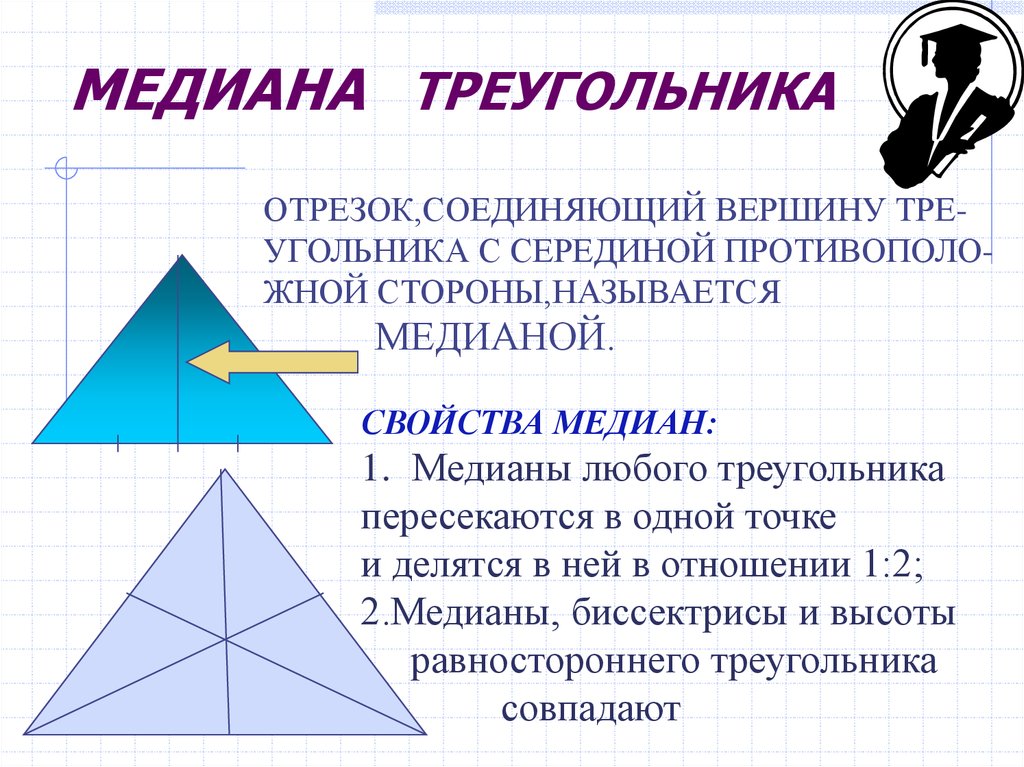
12. МЕДИАНА ТРЕУГОЛЬНИКА

ОТРЕЗОК,СОЕДИНЯЮЩИЙ ВЕРШИНУ ТРЕУГОЛЬНИКА С СЕРЕДИНОЙ ПРОТИВОПОЛОЖНОЙ СТОРОНЫ,НАЗЫВАЕТСЯ
МЕДИАНОЙ.
СВОЙСТВА МЕДИАН:
1. Медианы любого треугольника
пересекаются в одной точке
и делятся в ней в отношении 1:2;
2.Медианы, биссектрисы и высоты
равностороннего треугольника
совпадают

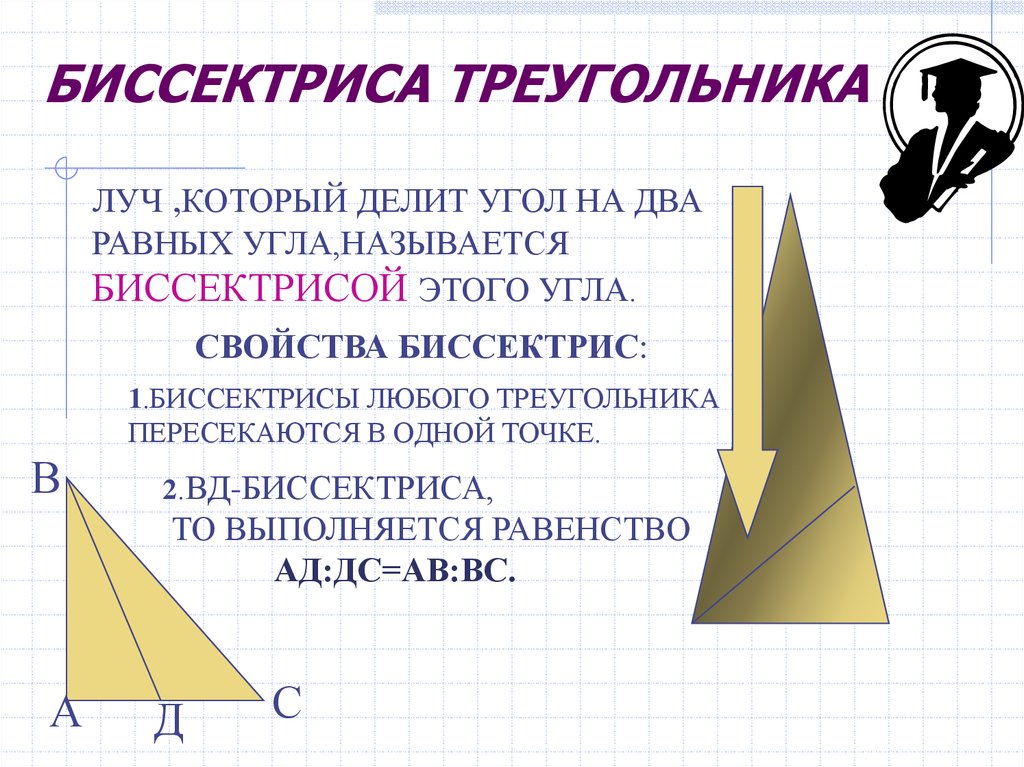
13. БИССЕКТРИСА ТРЕУГОЛЬНИКА

ЛУЧ ,КОТОРЫЙ ДЕЛИТ УГОЛ НА ДВА
РАВНЫХ УГЛА,НАЗЫВАЕТСЯ
БИССЕКТРИСОЙ ЭТОГО УГЛА.
СВОЙСТВА БИССЕКТРИС:
1.БИССЕКТРИСЫ ЛЮБОГО ТРЕУГОЛЬНИКА
ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ.
В
2.ВД-БИССЕКТРИСА,
ТО ВЫПОЛНЯЕТСЯ РАВЕНСТВО
АД:ДС=АВ:ВС.
А
Д
С

14.

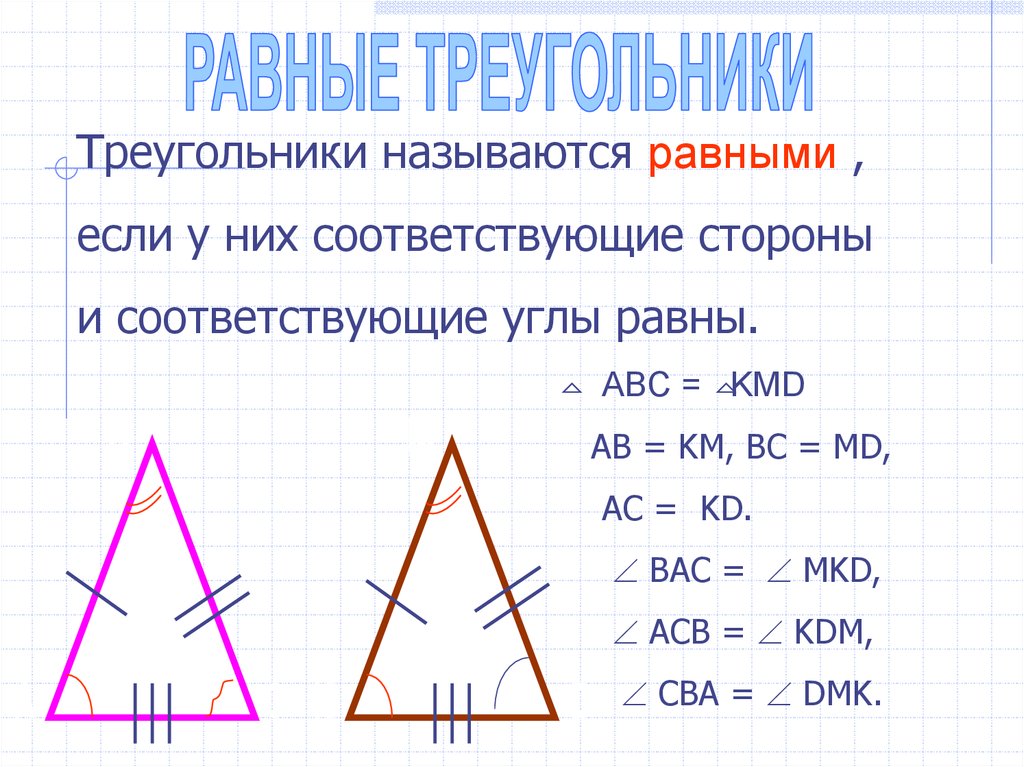
Треугольники называются равными ,
если у них соответствующие стороны
и соответствующие углы равны.
ABC = KMD
AB = KM, BC = MD,
AC = KD.
BAC = MKD,
ACB = KDM,
CBA = DMK.

15.

1. А А
1
В В
1
АВ
АС
2.
А1 В1 А1С1
А А1
АВ
ВС
АС А
3.
А1 В1 В1С1 А1С1
В1
В
С А1
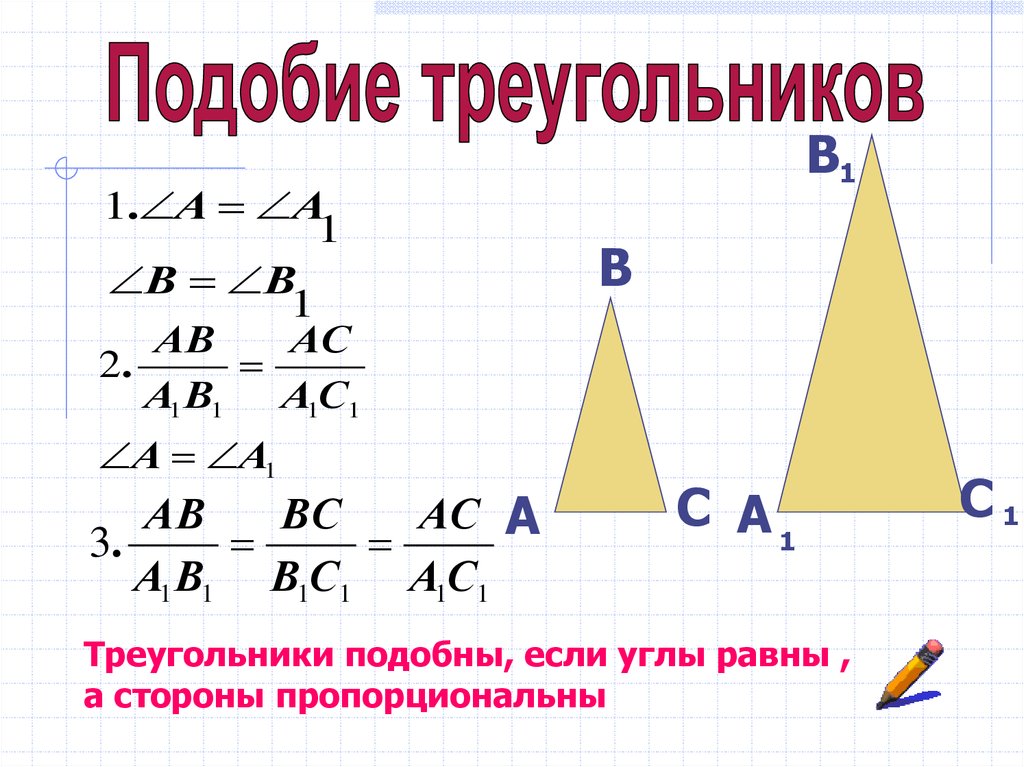
Треугольники подобны, если углы равны ,
а стороны пропорциональны
С1

16. Площадь треугольника

a b
S
sin
2
b h
S
2
a
b
c
m
a
a b
S
2
S
h
c
b
a
2
4
3

17.

Задачи
1. Две стороны равнобедренного треугольника равны
2см и 6 см. Найти основание (боковую сторону)
1)2 см ; 2) 6 см ;
3) 8 см ; 4) 4 см
2. Сторона равностороннего треугольника 18 3см.
Найти биссектрису ( медиану)этого треугольника.
1) 27 см
2) 9 3 см
3) 3 3 см 4) 9 см
3.Катеты прямоугольного треугольника 6 см и 8 см
(4 см и 9 см ). Найти его площадь.
1)48см 2 2)18см 2 3)36см 2 4)24см 2
4.В прямоугольном треугольнике высота, проведенная к
гипотенузе, разбивает её на отрезки длиной 12 см и
18 см .Найти длину большего (меньшего) катета.
1)15 2см2)10 6см3)6 15см4)6 10см