Похожие презентации:
Бесконечно убывающая геометрическая прогрессия. 10 класс
1.
Какая наука может быть более благородна,более восхитительна, более полезна для
человечества, чем математика? Франклин
Мыслить последовательно, судить
доказательно, опровергать неправильные
выводы должен уметь всякий: физик и
поэт, тракторист и химик.
Э.Кольман
В математике следует помнить не формулы,
а процессы мышления.
В.П.Ермаков
Легче найти квадратуру круга, чем
перехитрить математика. Огастес де Морган
2.
10 класс3. I. Арифметическая и геометрическая прогрессии. Вопросы
1. Определение арифметической прогрессии.Арифметической
прогрессией
называется прогрессии.
2.
Формула n-го члена
арифметической
последовательность, каждый член которой, начиная со
3.
Формула
суммы
первых nчлену,
членов
второго,
равен
предыдущему
сложенному с одним
n
1
n
и тем
же
числом.
арифметической
прогрессии
.
n
1
a d
a
a
2
a
d
n
1
1
n
1
4. S
Определение
прогрессии.
nгеометрической
S
n
a
a a d n 1
n
n
2
2
Геометрической
прогрессией
называется
5. Формула n-го члена геометрической прогрессии.
последовательность отличных от нуля чисел,
n 1каждый
b
b
q
bnФормула
b
q
,
b
0
член
которой,
начиная
со
второго,
равен
предыдущему
n
1
1
6.
суммы
первых
n
членов
геометрической
1
n
n
n же число
члену,
умноженному
на одноbи q
то
прогрессии
.
1
Sn
1
q 1
, q 1
4. II. Арифметическая прогрессия. Задания
1. Арифметическая прогрессия задана формулой an = 7 – 4n(-33)
Найдите a10.
2. В арифметической прогрессии a3 = 7 и a5 = 1.
Найдите a4 .
3. В арифметической прогрессии a3 = 7 и a5 = 1.
Найдите a17.
4. В арифметической прогрессии a3 = 7 и a5 = 1.
Найдите S17.
(4)
(-35)
(-187)
5. II. Геометрическая прогрессия. Задания
5. Для геометрической прогрессиинайдите пятый член
2 2
2; ; ;...
3 9
2
81
6. Для геометрической прогрессии
найдите n-й член.
2 2
2; ; ;...
3 9
1
2
3
7. В геометрической прогрессии
b3 = 8 и b5 = 2.
8. В геометрической прогрессии
b3 = 8 и b5 = 2.
9. В геометрической прогрессии
b3 = 8 и b5 = 2.
Найдите b4.
Найдите b1 и q.
Найдите S5.
n 1
(4)
1
и
32
2
(62)
6.
7.
8.
n1
0
n
2
9.
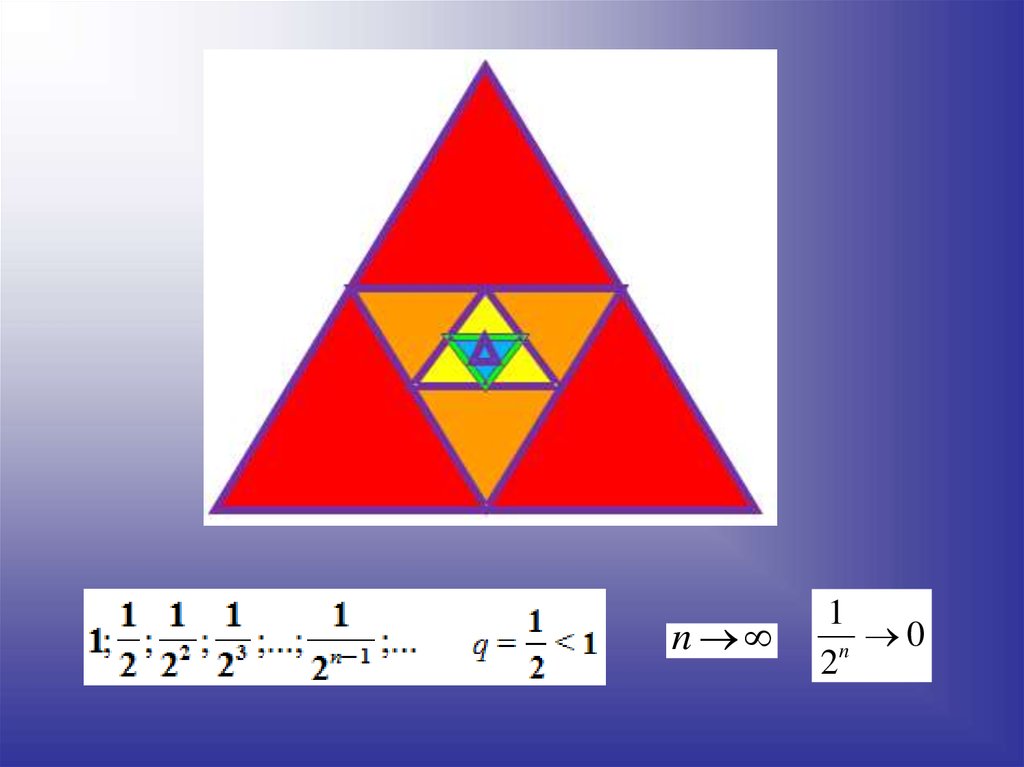
определение:Геометрическая прогрессия называется
бесконечно убывающей, если модуль её
знаменателя меньше единицы.
q 1
10. Задача №1
Является ли последовательность бесконечноубывающей геометрической прогрессией, если
она заданна формулой:
10
а )bn n
7
б)bn 4
n 2
Решение: а)
b1
10
7
10
b2
49
10 10 1
q
:
49 7 7
1
1
7
данная геометрическая прогрессия является бесконечно убывающей.
б)
данная последовательность не является бесконечно убывающей
геометрической прогрессией.
11.
1lim n 0
n 2
1
lim 1 n 1
n
2
lim S n 1
n
12.
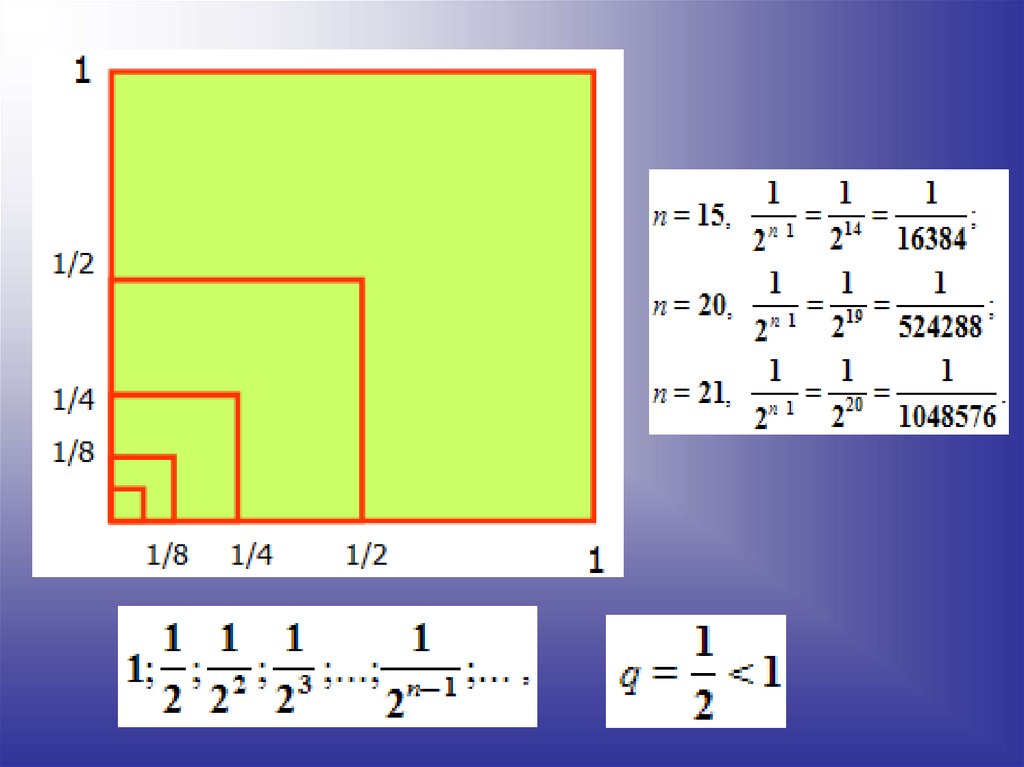
Сумма бесконечно убывающей геометрической прогрессииесть предел последовательности S1, S2, S3, …, Sn, … .
1 1 1
1
1
,
,
,
,...,
гдеb
1
,
q
Например, для прогрессии
1
3 9 27
3
имеем
Так как
n
1
1 1
1 2
1 1 7
3 3 3 1 n
S1 1, S 2 1 , S3 1 ,..., S n
,...
3 3
3 9 9
4 4 3
1
1
3
n
3
1
lim 0, то lim S n .
n
n
4
3
Сумму бесконечно убывающей геометрической прогрессии
можно находить по формуле
S
b1
1 q
13. Выполнение заданий
1. Найти сумму бесконечно убывающей геометрическойпрогрессии с первым членом 3, вторым 0,3.
2. №13;
3. №15(1;3);
4. №19;
№14;
№16(1;3) №18(1;3);
№20.
учебник, стр. 138
14. Вопросы
• С какой последовательностью сегодняпознакомились?
• Дайте определение бесконечно
убывающей геометрической прогрессии.
• Как доказать, что геометрическая
прогрессия является бесконечно
убывающей?
• Назовите формулу суммы бесконечно
убывающей геометрической прогрессии.
15. На дом:
• 1. Читать § 2 (с. 133-137)• 2. № 15(2;4), № 16(2;4), №18(2;4)
16.
• Известный польскийматематик Гуго Штейнгаус
шутливо утверждает, что
существует закон, который
формулируется так:
математик сделает это
лучше. А именно, если
поручить двум людям, один
из которых математик,
выполнение любой
незнакомой им работы, то
результат всегда будет
следующим: математик
сделает ее лучше.
Гуго Штейнгаус
14.01.1887-25.02.1972














 Математика
Математика








