Линейные неравенства с параметром

1.

Работу подготовила
Коваленко Ирина Анатольевна,
учитель математики школы №3
город Стародуб Брянская область

2.

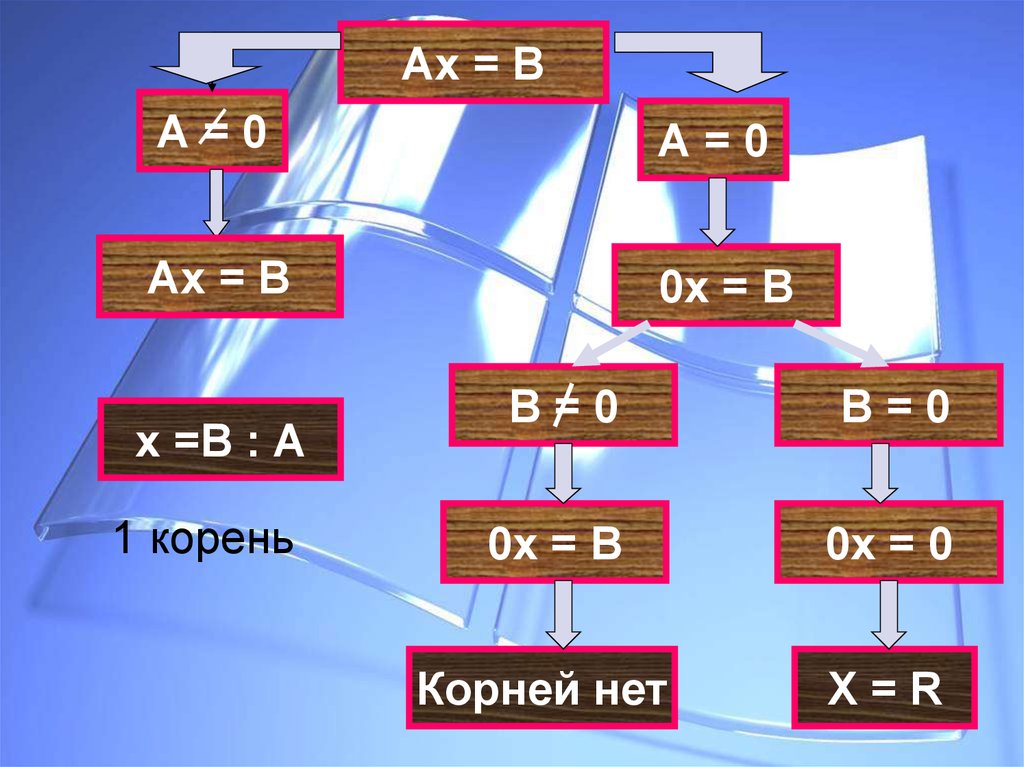
Ах = В
А=0
А=0
Ах = В
0х = В
х =В : А
1 корень
В=0
В=0
0х = В
0х = 0
Корней нет
Х=R

3. Алгоритм решения линейных уравнений с параметром

1.Найти ДЗП ( допустимые
значения параметра).
2. На ДЗП привести уравнение к
стандартному виду.
3. Найти КЗП и решить частные
уравнения.
4. Решить общие уравнения.
5. Нанести все решения на ось
параметра.
6. Записать ответ.

4.

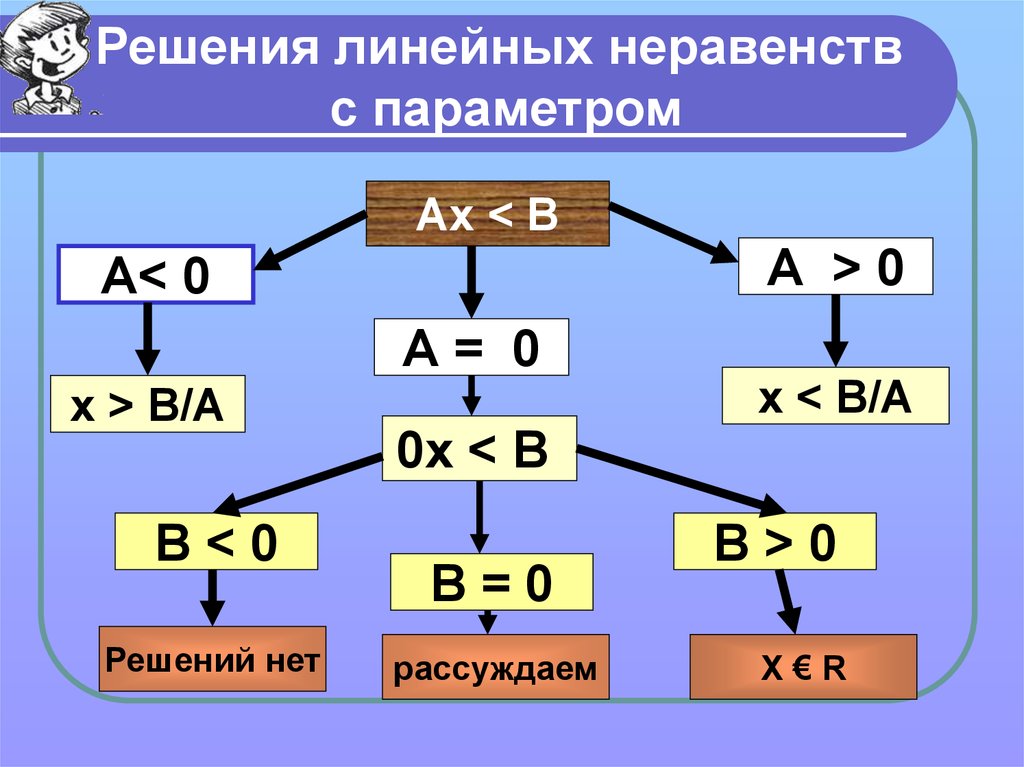
Решения линейных неравенств
с параметром
Ах < В
А< 0
А= 0
х > В/А
В<0
Решений нет
0х < В
В=0
рассуждаем
А >0
х < В/А
В>0
Х€R

5.

Неравенства с двумя переменными а и х
вида F(x,a) >< 0 называется
неравенством с переменной х и
параметром а, если для любого значения
а надо решить соответствующие
частные неравенства относительно х

6. Пример: Решить неравенство 3(2а – х) < ах + 1

Пример: Решить неравенство
3(2а – х) < ах + 1
6а – 3х <ах + 1 ( первая степень
переменной х – линейное
неравенство)
1. ОДЗП: а – любое число
2. -3х –ах < 1-6а
( 3 + а)х > 6а -1.
3. КЗП: 3 +а =0, а = -3.
При а = -3 имеем: 0х > -19, х – любое число.

7. 4. Рассмотрим ось параметров.

х <(6а -1) / ( а+3)
Х – любое
число
-3
х > (6а -1) / ( а+3)
а
4. При а <-3 3 + а < 0, тогда
х <(6а -1) / ( а+3)
При а >-3 3 + а > 0, тогда х > (6а -1) / ( а+3)
5. Ответ

8.

Алгоритм решения линейных
неравенств с параметром
1. Найти ОДЗ параметра.
2. Привести на ОДЗП неравенство к стандартному
виду.
3. Найти КЗП и решить частные неравенства.
4. Решить неравенство на каждом промежутке.
5. Нанести полученное на ось параметров.
6. Записать ответ.