Похожие презентации:
Прямая. Парабола. Гипербола. Корень
1.
ПрямаяПарабола
Гипербола
Корень
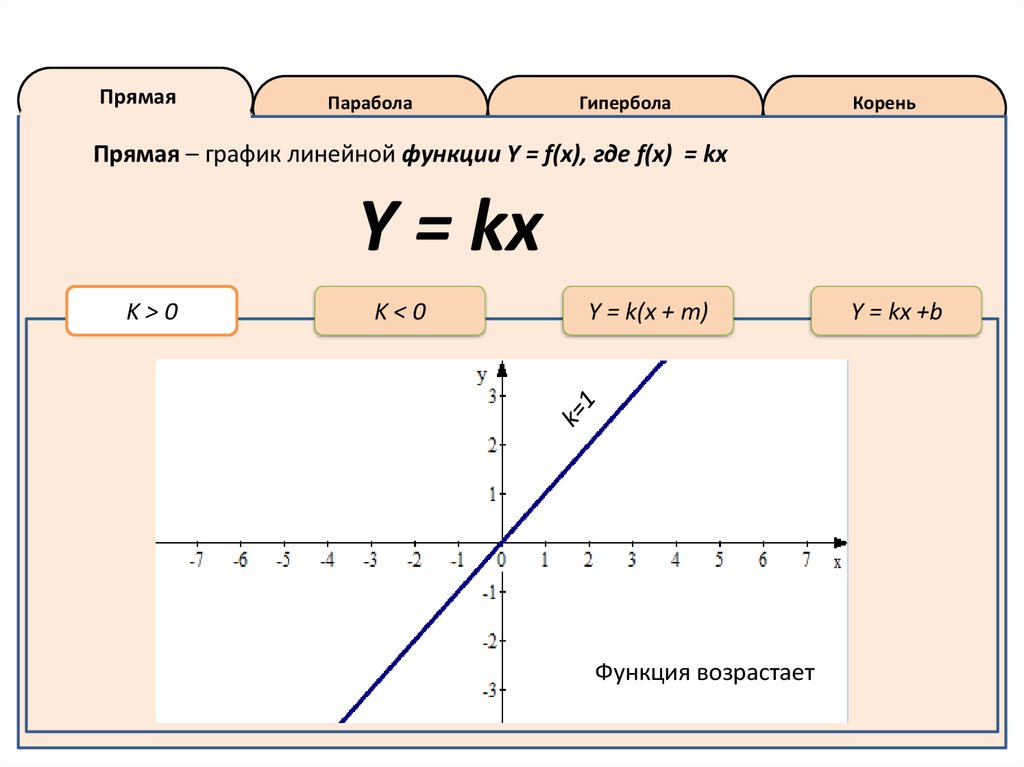
Прямая – график линейной функции Y = f(x), где f(x) = kx
Y = kx
K>0
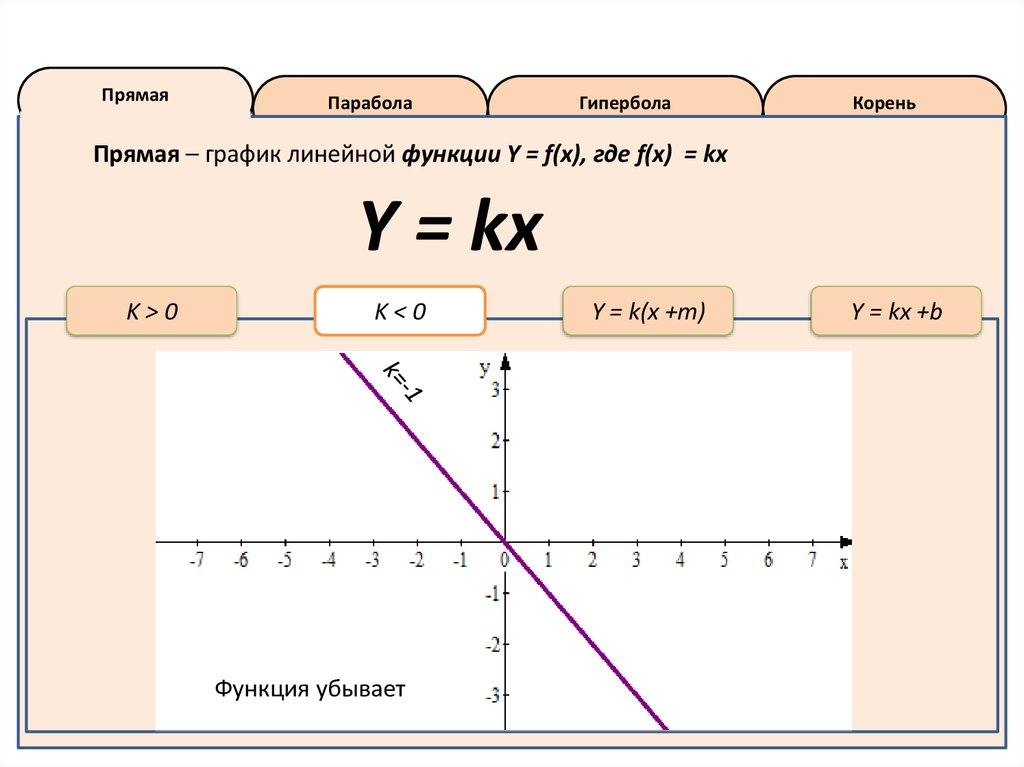
K<0
Y = k(x + m)
Функция возрастает
Y = kx +b
2.
ПрямаяПарабола
Гипербола
Корень
Прямая – график линейной функции Y = f(x), где f(x) = kx
Y = kx
K>0
K<0
Функция убывает
Y = k(x +m)
Y = kx +b
3.
ПрямаяПарабола
Гипербола
Корень
Прямая – график линейной функции Y = f(x), где f(x) = kx
Y = kx
K>0
K<0
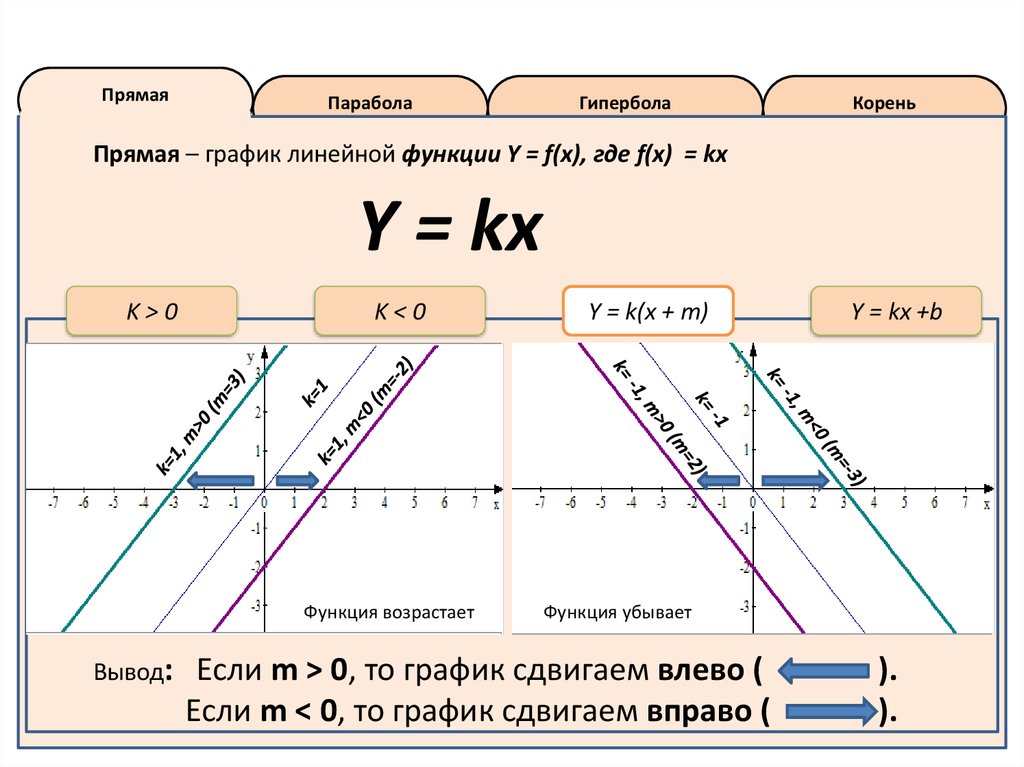
Функция возрастает
Вывод:
Y = k(x + m)
Y = kx +b
Функция убывает
Если m > 0, то график сдвигаем влево (
Если m < 0, то график сдвигаем вправо (
).
).
4.
ПрямаяПарабола
Гипербола
Корень
Прямая – график линейной функции Y = f(x), где f(x) = kx
Y = kx
K>0
K<0
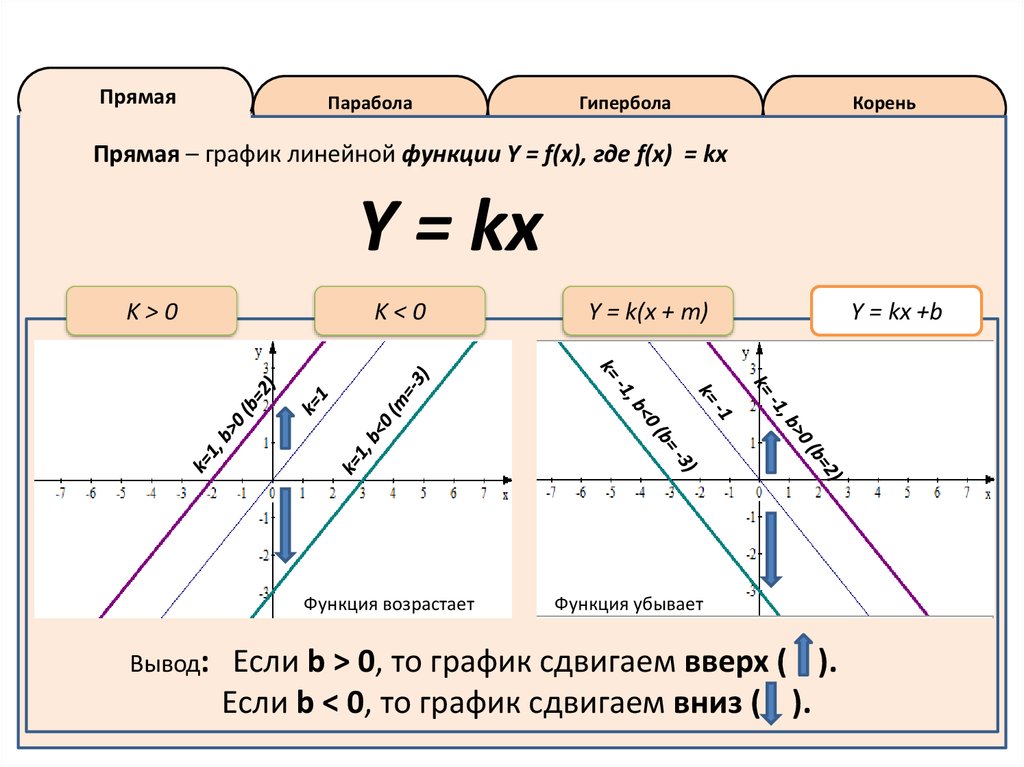
Функция возрастает
Вывод:
Y = k(x + m)
Функция убывает
Если b > 0, то график сдвигаем вверх ( ).
Если b < 0, то график сдвигаем вниз ( ).
Y = kx +b
5.
ПрямаяПарабола
Гипербола
Корень
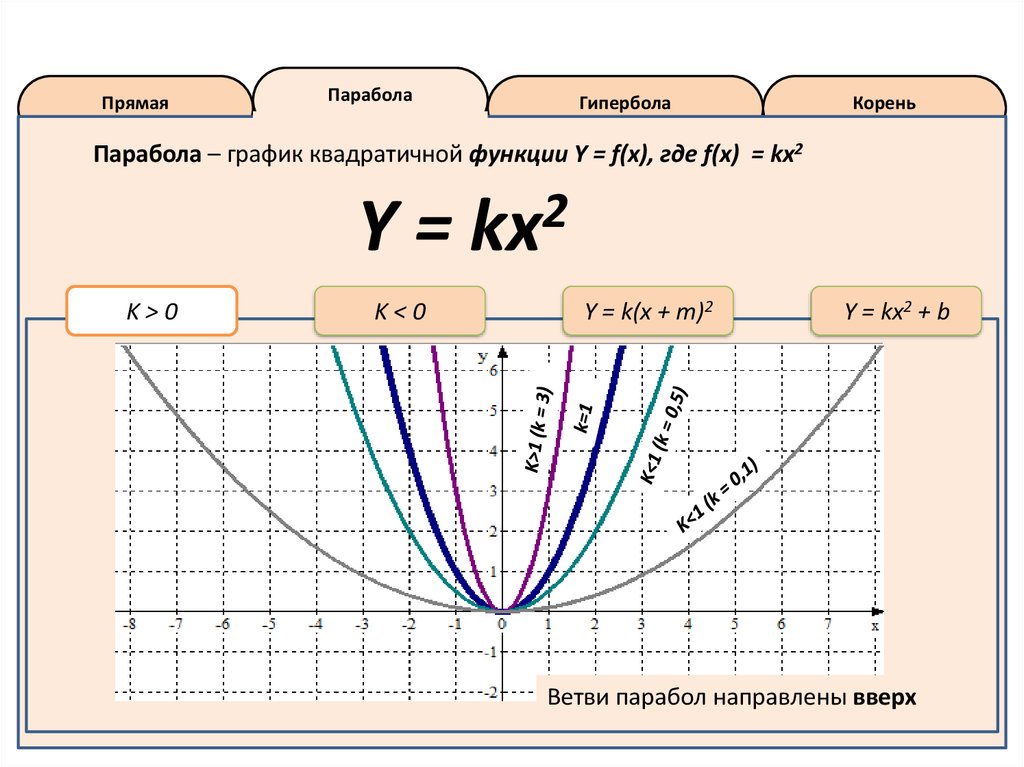
Парабола – график квадратичной функции Y = f(x), где f(x) = kx2
Y=
K>0
K<0
2
kx
Y = k(x + m)2
Y = kx2 + b
Ветви парабол направлены вверх
6.
ПрямаяПарабола
Гипербола
Корень
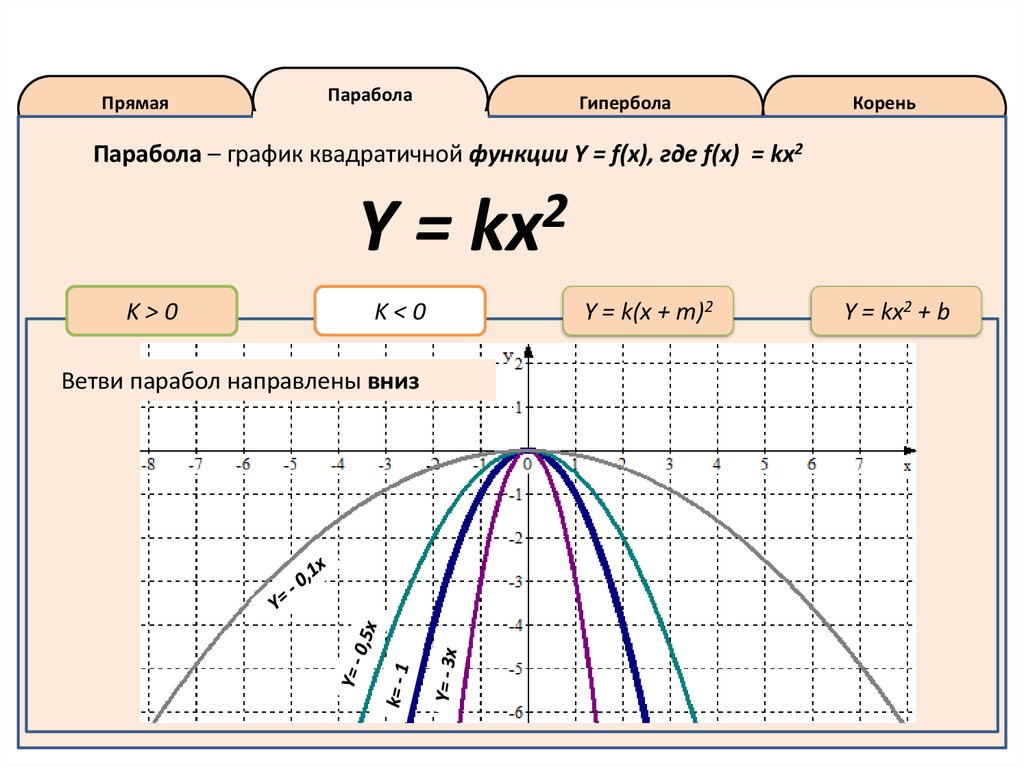
Парабола – график квадратичной функции Y = f(x), где f(x) = kx2
Y=
K>0
K<0
Ветви парабол направлены вниз
2
kx
Y = k(x + m)2
Y = kx2 + b
7.
ПрямаяПарабола
Гипербола
Корень
Парабола – график квадратичной функции Y = f(x), где f(x) = kx2
Y=
K>0
K<0
2
kx
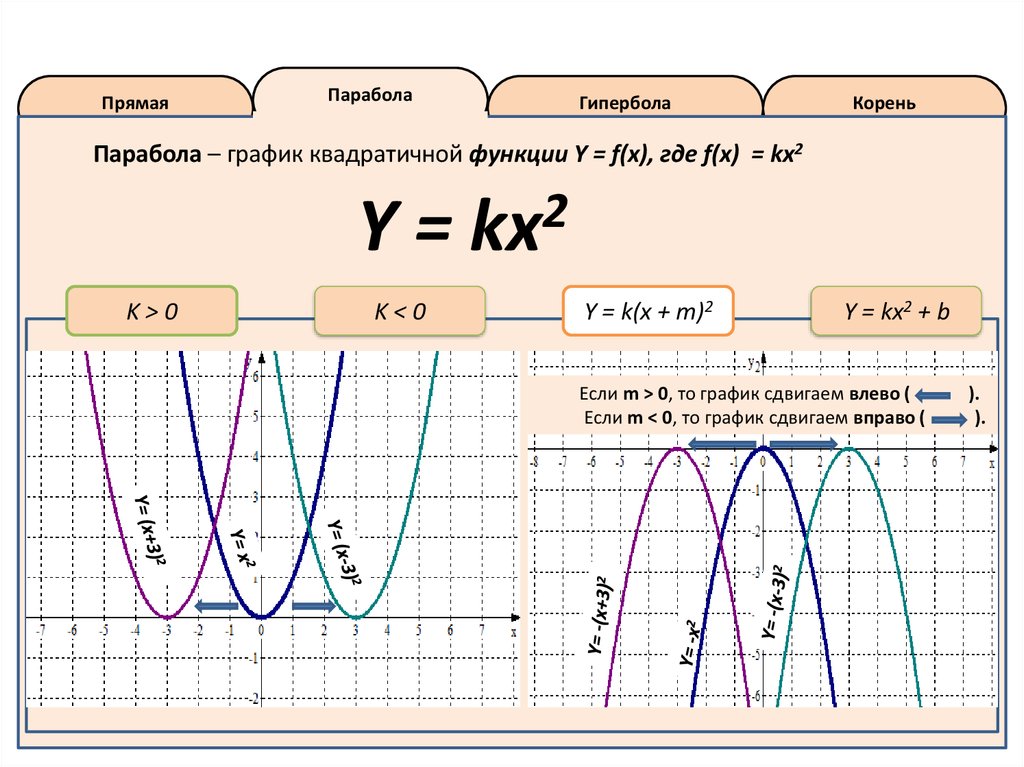
Y = k(x + m)2
Y = kx2 + b
Если m > 0, то график сдвигаем влево (
Если m < 0, то график сдвигаем вправо (
).
).
8.
ПараболаПрямая
Гипербола
Корень
Парабола – график квадратичной функции Y = f(x), где f(x) = kx2
Y=
K>0
K<0
2
kx
Y = k(x + m)
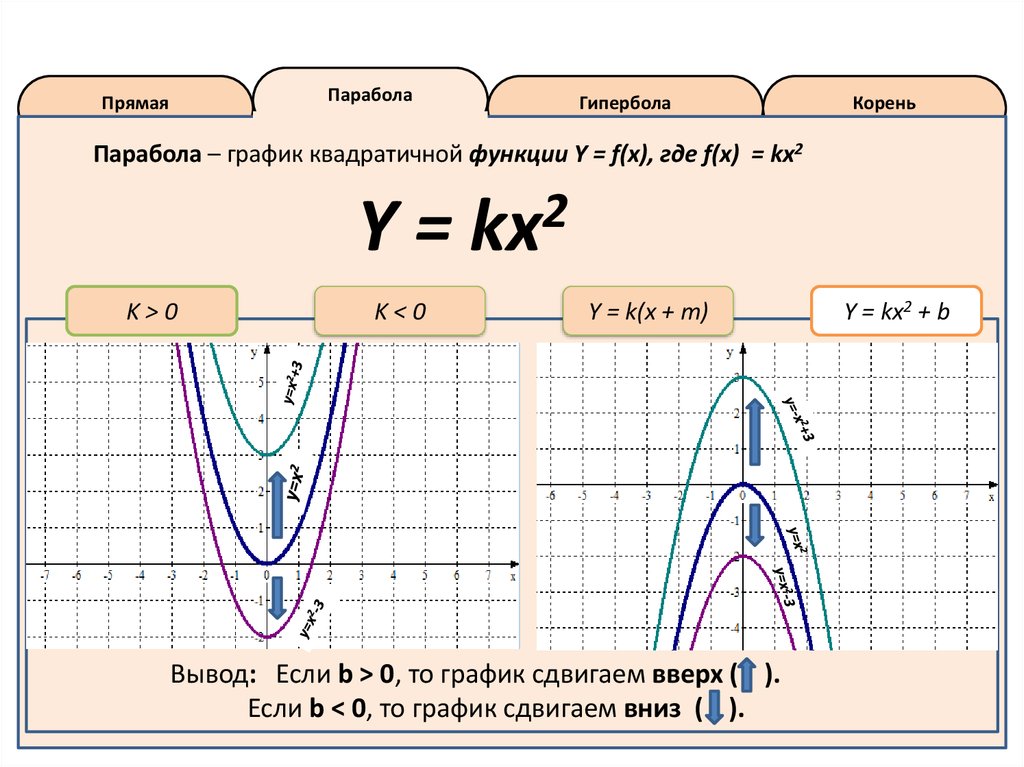
Вывод: Если b > 0, то график сдвигаем вверх ( ).
Если b < 0, то график сдвигаем вниз ( ).
Y = kx2 + b
9.
ПрямаяПарабола
Гипербола
Корень
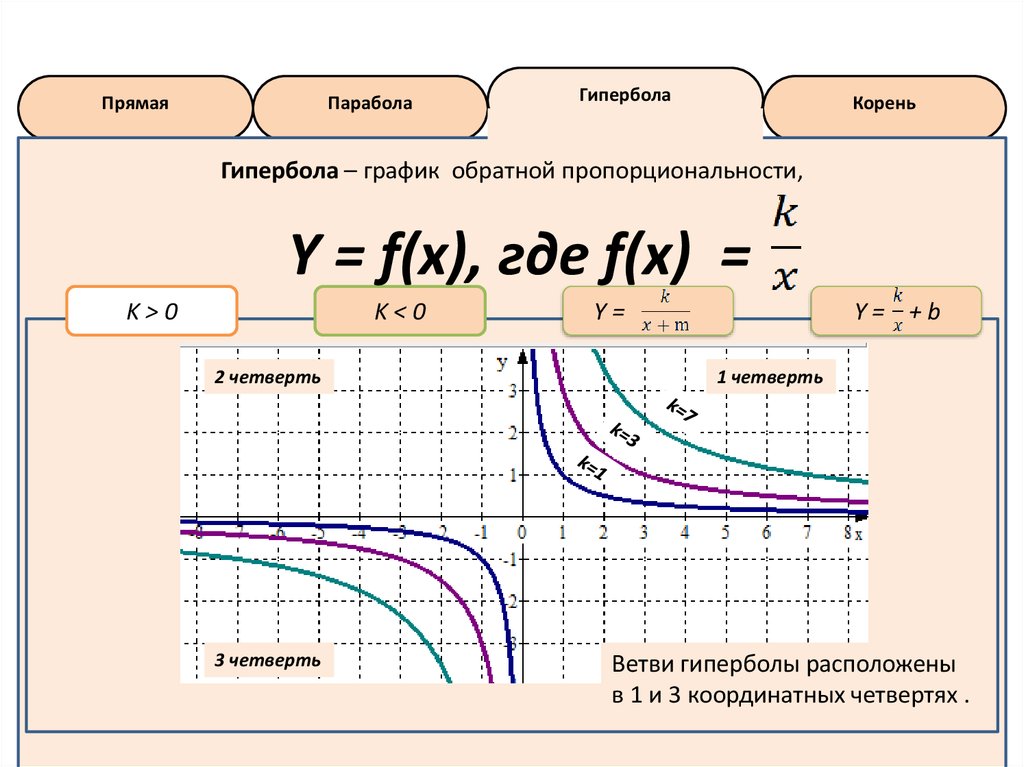
Гипербола – график обратной пропорциональности,
Y = f(x), где f(x) =
K>0
K<0
2 четверть
3 четверть
Y=
Y= +b
1 четверть
Ветви гиперболы расположены
в 1 и 3 координатных четвертях .
10.
ПрямаяПарабола
Гипербола
Корень
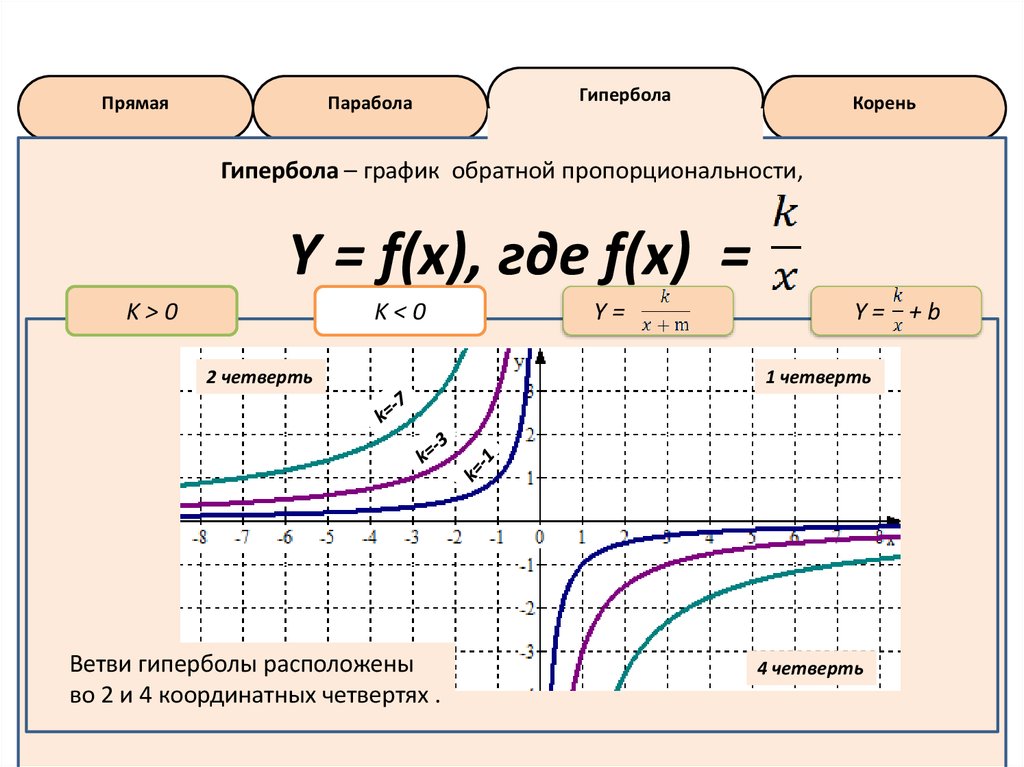
Гипербола – график обратной пропорциональности,
Y = f(x), где f(x) =
K>0
K<0
2 четверть
Ветви гиперболы расположены
во 2 и 4 координатных четвертях .
Y=
Y= +b
1 четверть
4 четверть
11.
ПрямаяГипербола
Парабола
Корень
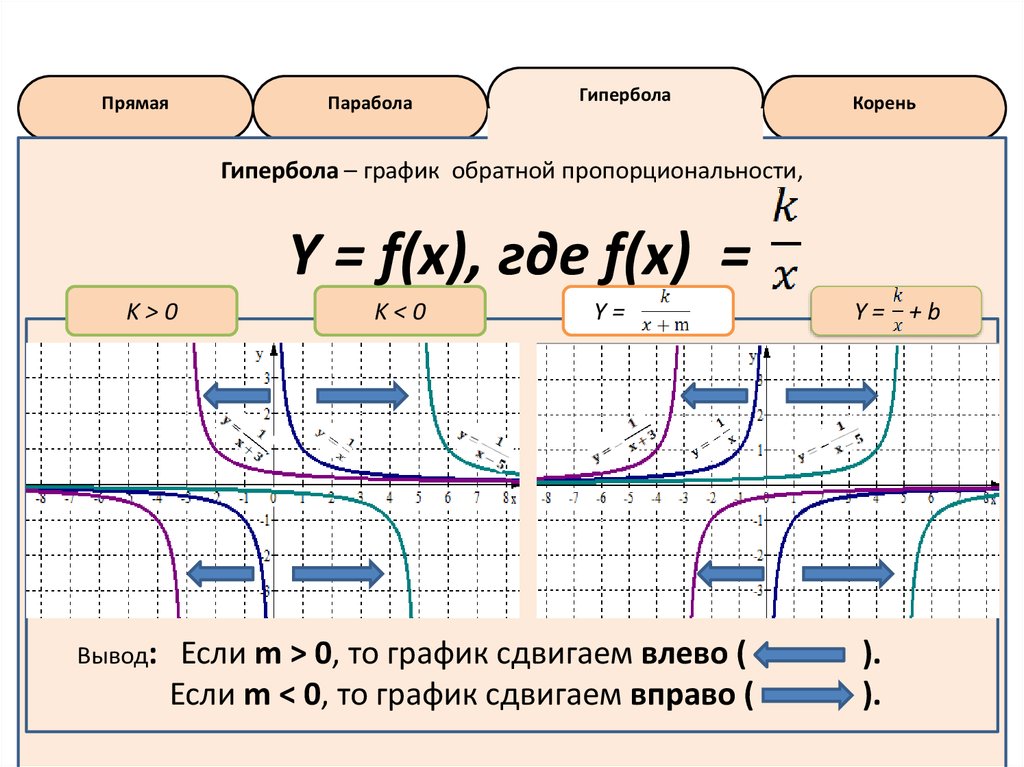
Гипербола – график обратной пропорциональности,
Y = f(x), где f(x) =
K>0
K<0
Y=
Y= +b
=
Вывод:
Если m > 0, то график сдвигаем влево (
Если m < 0, то график сдвигаем вправо (
).
).
12.
ПрямаяПарабола
Гипербола
Корень
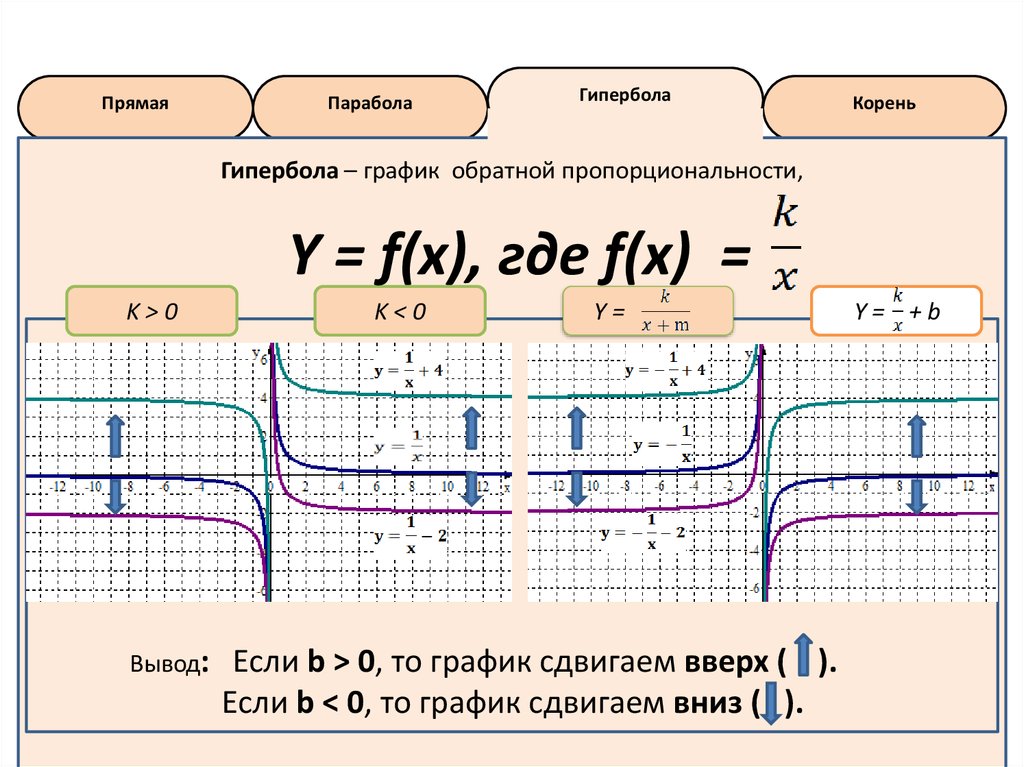
Гипербола – график обратной пропорциональности,
Y = f(x), где f(x) =
K>0
Вывод:
K<0
Y=
Если b > 0, то график сдвигаем вверх ( ).
Если b < 0, то график сдвигаем вниз ( ).
Y= +b
13.
ПрямаяПарабола
Корень
Гипербола
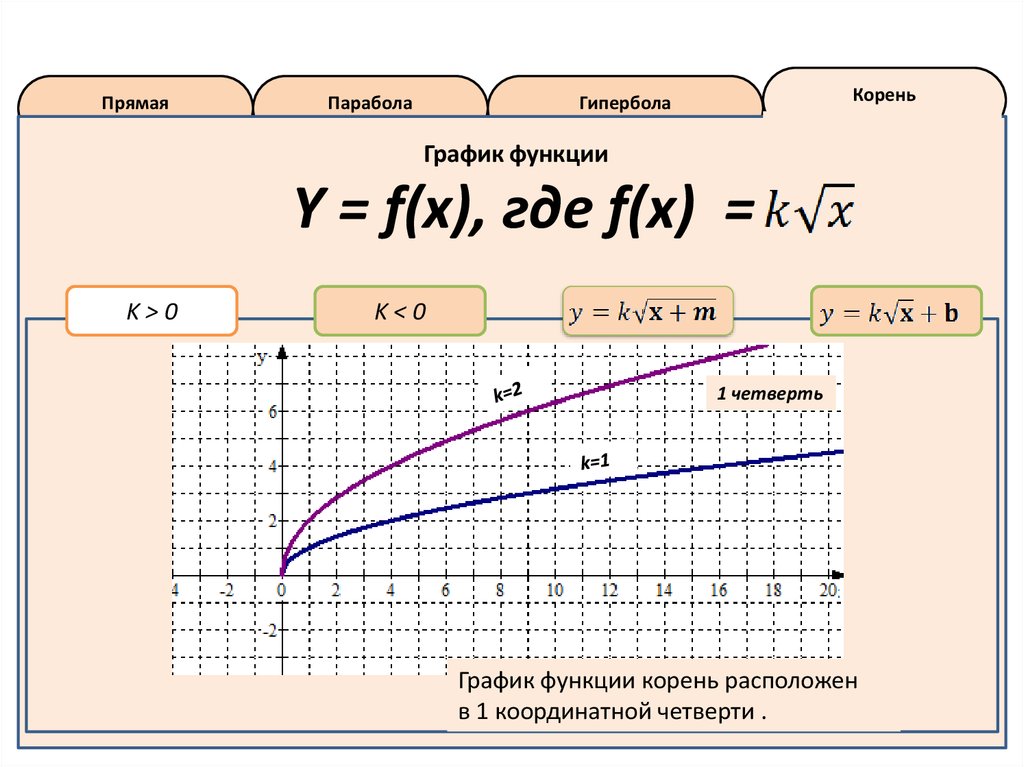
График функции
Y = f(x), где f(x) =
K>0
K<0
1 четверть
График функции корень расположен
в 1 координатной четверти .
14.
ПрямаяПарабола
Корень
Гипербола
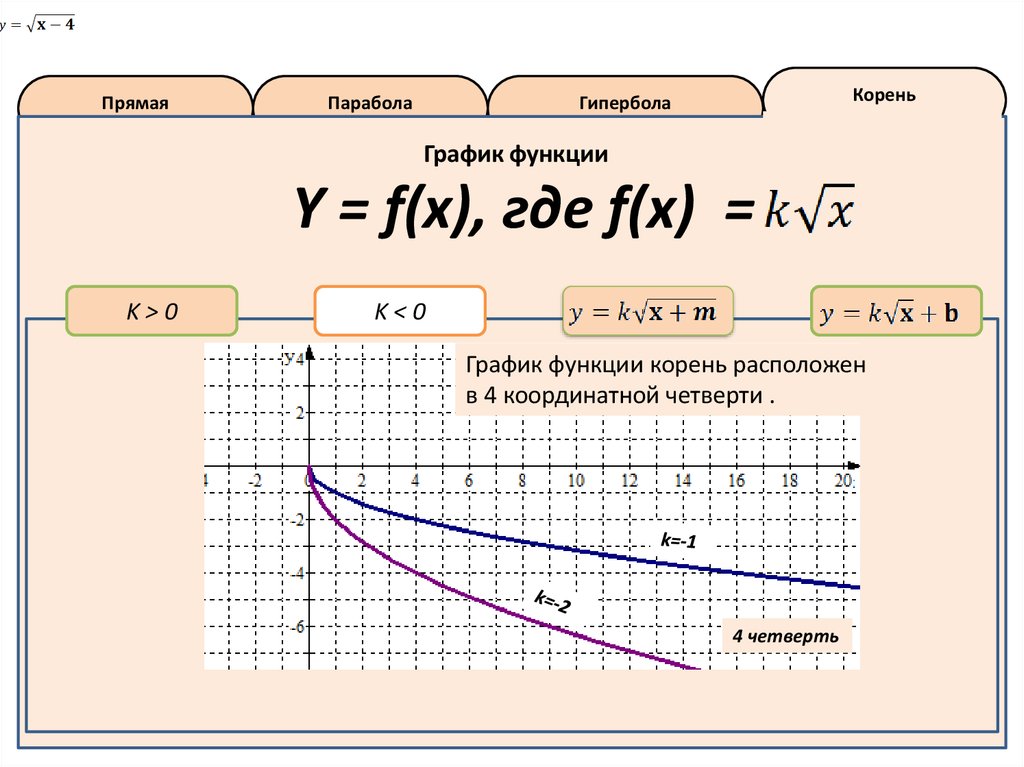
График функции
Y = f(x), где f(x) =
K>0
K<0
График функции корень расположен
в 4 координатной четверти .
4 четверть
15.
ПрямаяПарабола
Гипербола
Корень
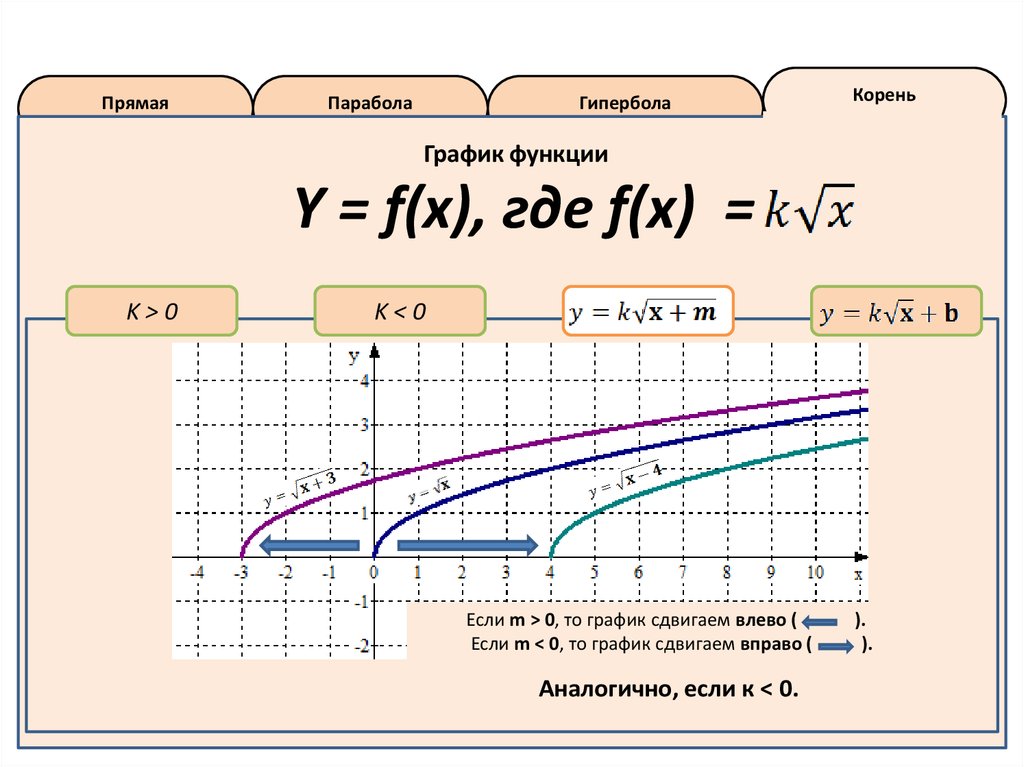
График функции
Y = f(x), где f(x) =
K>0
K<0
Если m > 0, то график сдвигаем влево (
Если m < 0, то график сдвигаем вправо (
Аналогично, если к < 0.
).
).
16.
ПрямаяПарабола
Гипербола
Корень
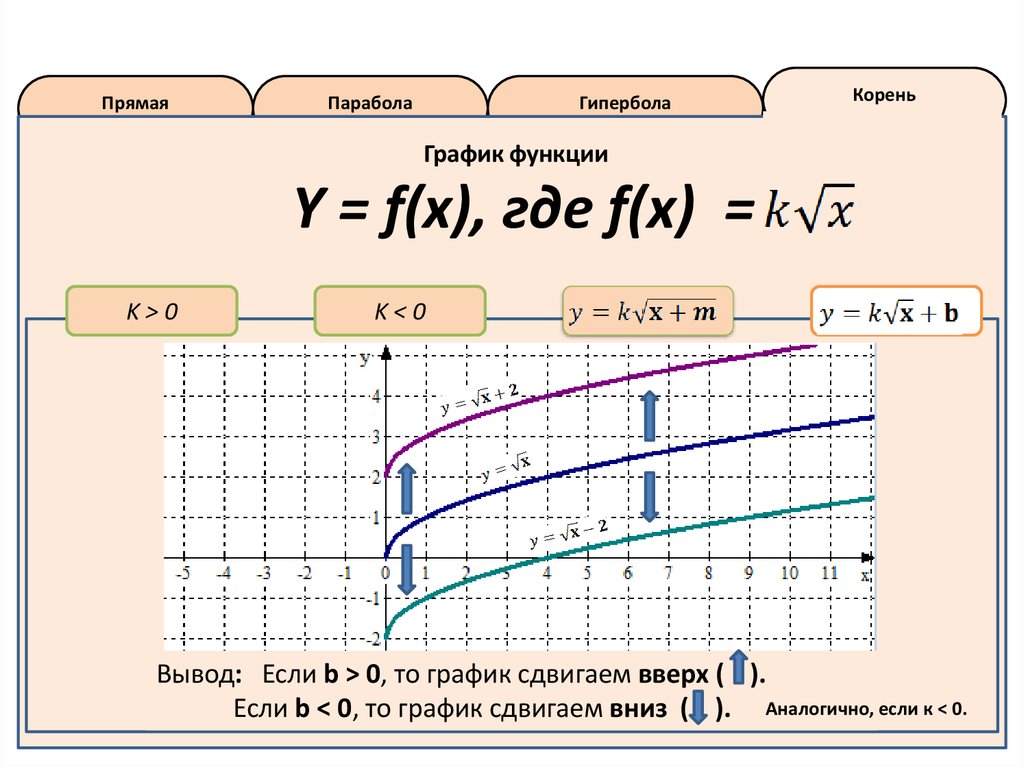
График функции
Y = f(x), где f(x) =
K>0
K<0
Вывод: Если b > 0, то график сдвигаем вверх ( ).
Если b < 0, то график сдвигаем вниз ( ). Аналогично, если к < 0.
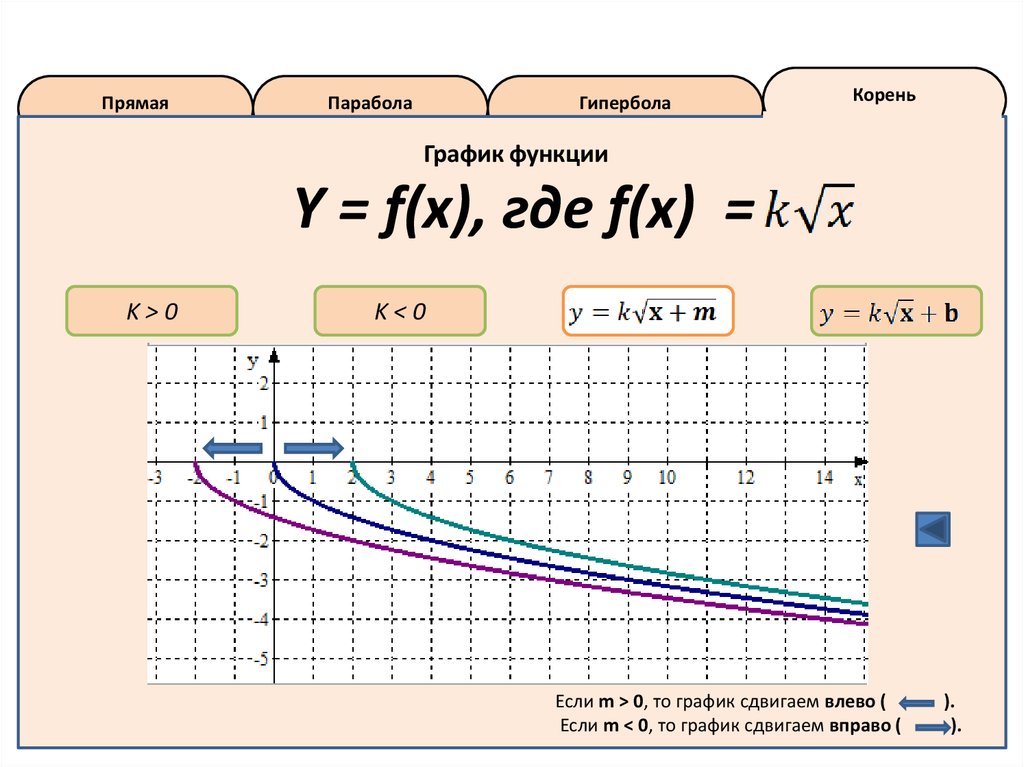
17.
ПрямаяПарабола
Гипербола
Корень
График функции
Y = f(x), где f(x) =
K>0
K<0
Если m > 0, то график сдвигаем влево (
Если m < 0, то график сдвигаем вправо (
).
).
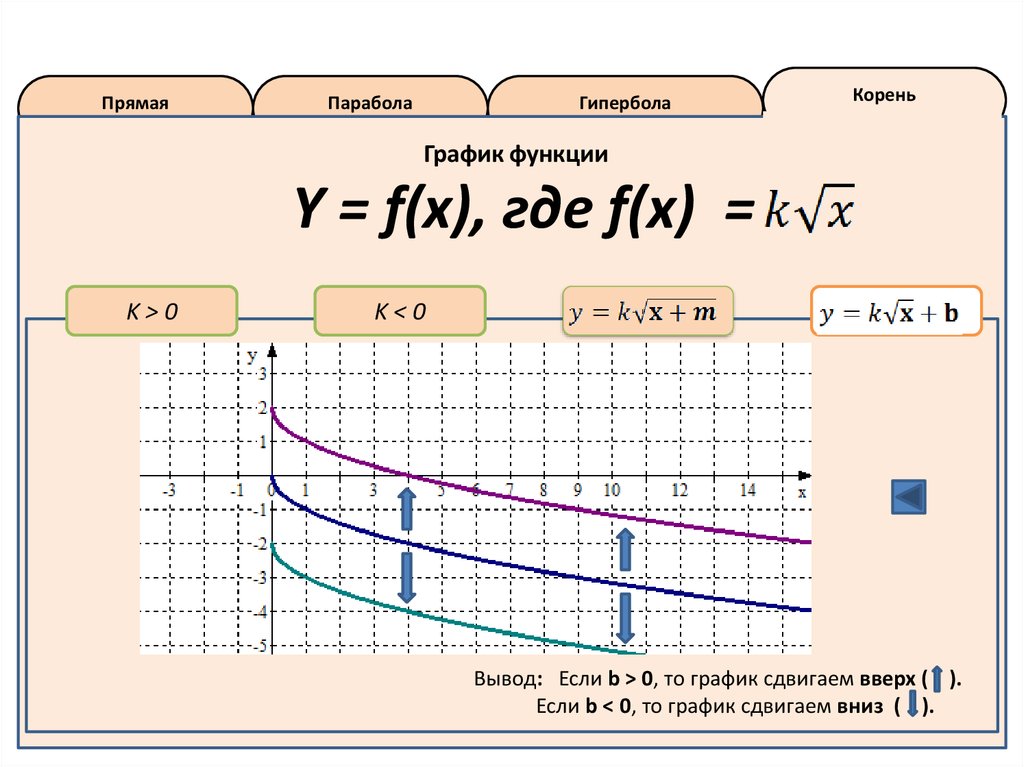
18.
ПрямаяПарабола
Гипербола
Корень
График функции
Y = f(x), где f(x) =
K>0
K<0
Вывод: Если b > 0, то график сдвигаем вверх ( ).
Если b < 0, то график сдвигаем вниз ( ).
 Математика
Математика








