Функции, пределы, непрерывности

1. Функции, пределы, непрерывности.

2. Основные вопросы:

Понятие предела функции.
Основные теоремы о пределах
функций (
).
Методы вычисления пределов
на неопределенность( 0 с с ).
, ,
0 0

3. Предел функции

ПРЕДЕЛ ФУНКЦИИ
–
одно
из
основных
понятий
математического анализа. Понятие предела использовалось
еще Ньютоном во второй половине XVII века и математиками
XVIII века, такими как Эйлер и Лагранж, однако они понимали
предел интуитивно. Первые строгие определения предела дали
Больцано в 1816 году и Коши в 1821 году.

4.

lim f ( x) В
В
x a
f (a ) не существует

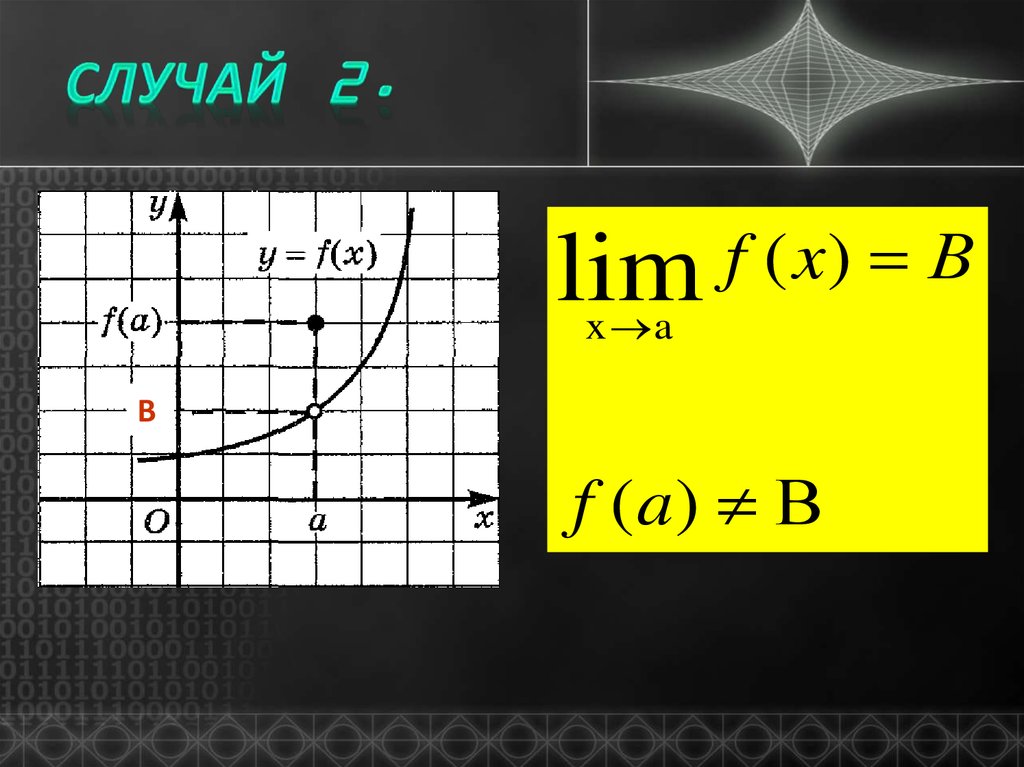
5.

lim f ( x) В
x a
В
f (a) В

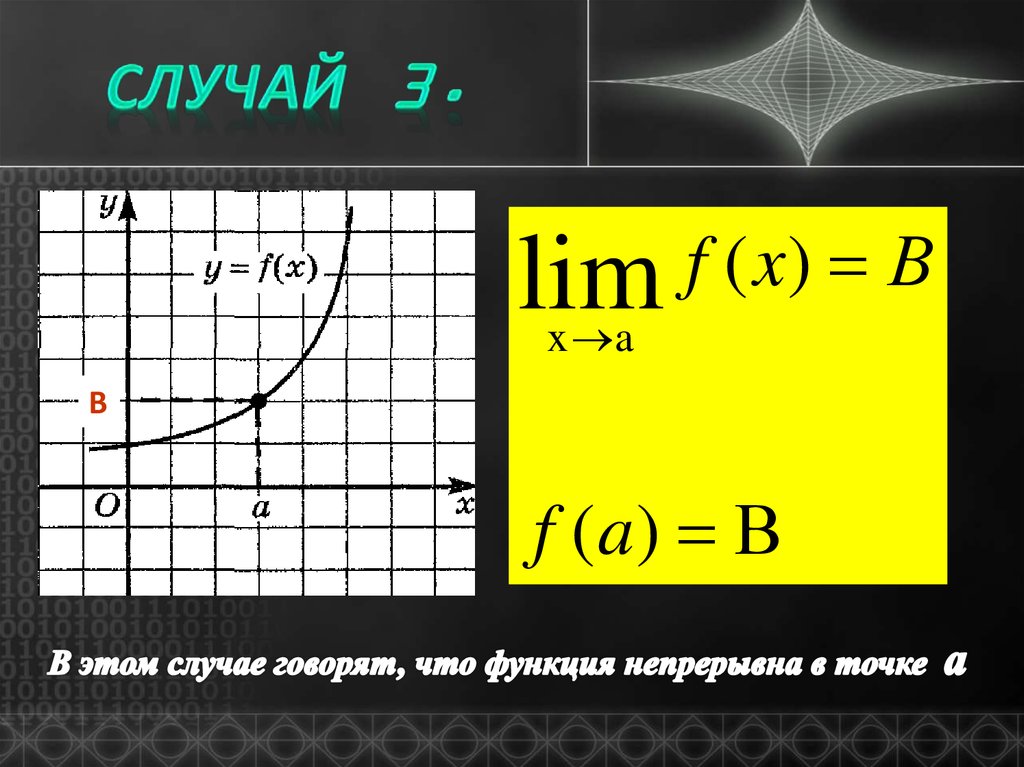
6.

lim
f ( x) В
x a
В
f (a) В

7.

Предел функции

8. Предел функции в точке

Число В называется пределом
функции в точке а, если для всех
значений х , достаточно близких к а
и отличных от а, значение функции
f (x) сколь угодно мало отличается
от В.
lim f ( x ) b
x a

9.

lim ( f ( x) g ( x)) lim f ( x) lim g ( x)
x x0
x x0
x x0

10.

lim C C
x x0

11.

lim ( f ( x) g ( x)) lim f ( x) lim g ( x)
x x0
x x0
x x0

12.

lim f ( x)
f ( x) x x0
lim
, если _ lim g ( x) 0
x x0 g ( x)
x x0
lim g ( x)
x x0

13.

lim (k f ( x)) k lim f ( x)
x x0
x x0

14.

lim ( z ) (lim z)
n
x a
x a
n

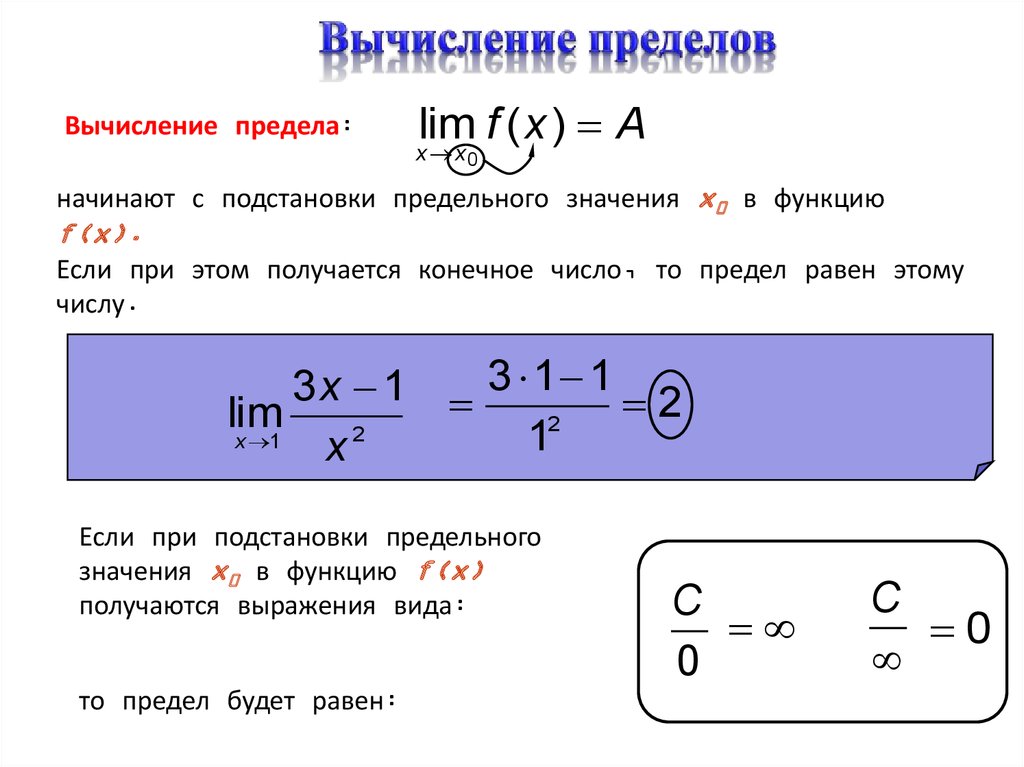
15. Вычисление пределов

Вычисление предела:
lim f ( x ) A
x x0
начинают с подстановки предельного значения x0 в функцию
f(x).
Если при этом получается конечное число, то предел равен этому
числу.
3x 1 3 1 1 2
lim
2
2
x 1
1
x
Если при подстановки предельного
значения x0 в функцию f(x)
получаются выражения вида:
то предел будет равен:
C
0
C
0

16. Вычислить пределы:

lim ( x 7 x 4) 3 7 3 4 8;
2
2
x 3
x 2
( x 2)( x 2)
x2 4
2;
lim
lim
lim 2
x 2
x 2
x 2 x 2 x
x
x( x 2)
3
)
x
)(
2
x
(
2
2
(0 / 0)
2x 3
2x 7x 6
2
;
lim
lim
lim
2
2
x 2 x 2
x 2
x 2
( x 2)
( x 2)

17.

Примеры

18. Последовательности, пределы.

19. Вычисление пределов

Часто при подстановке предельного значения x0 в
функцию f(x) получаются выражения следующих
видов:
0
;
0
; 0 ; 1 ; 0 0 ; 0 ; 0 ;
Эти выражения называются
а
вычисление пределов в этом случае называется
.

20. Методы вычисления пределов на неопределенность

0 с с
, ,
0 0
3x 2 x 0 0 0
lim 2
x 0 2 x 5 x
0 0 0
2
это значит найти
предел (если он существует)
соответствующего выражения, что,
однако не всегда просто.

21.

В большинстве случаев, чтобы раскрыть
0
неопределенность вида
,
0

22.

3x 2 2 x 0
lim 2
x 0 2 x 5 x
0
x 3x 2
3x 2 2
lim
lim
x 0 x 2 x 5
x 0 2 x 5
5

23.

lim 4 x
4x
4*0
0
x 0
lim 2
2
x 0 3 x 2 x
lim 3x 2 x 3 * 0 2 * 0 0
x 0
4x
4
4
lim
lim
2.
x 0 x 3 x 2
x 0 3 x 2
3* 0 2

24.

Чтобы раскрыть неопределенность
данного вида, зависящую от
иррациональности,

25. Раскрытие неопределенностей

Раскрытие неопределенности
0
0
x 2 14 x 32
0
x 2 x 16
lim 2
lim
x 2
x 2
x 6x 8
0
x 2 x 4
x 16 18
lim
9
x 2
x 4
2
Если f(x) – дробно –
рациональная
x 1 1 x 1 1
0
x 1 1 функция,
наlim Если f(x) – иррациональная
lim необходимо разложить
x 0
0
множители
числитель
иx 0 дробь, x
x
x 1 умножить
1
необходимо
знаменатель дроби
числитель и знаменатель
x 1 1
1дроби на выражение,
1
lim
lim
числителю.
x 0
x 0
сопряженное
x x 1 1
x 1 1 2

26.

26

27.

,0 ,
lim (2 x 1)
3
x
1
lim
0
x x 3
x 5
lim
x 2 x

28.

29.

Чтобы раскрыть неопределенность
вида
,

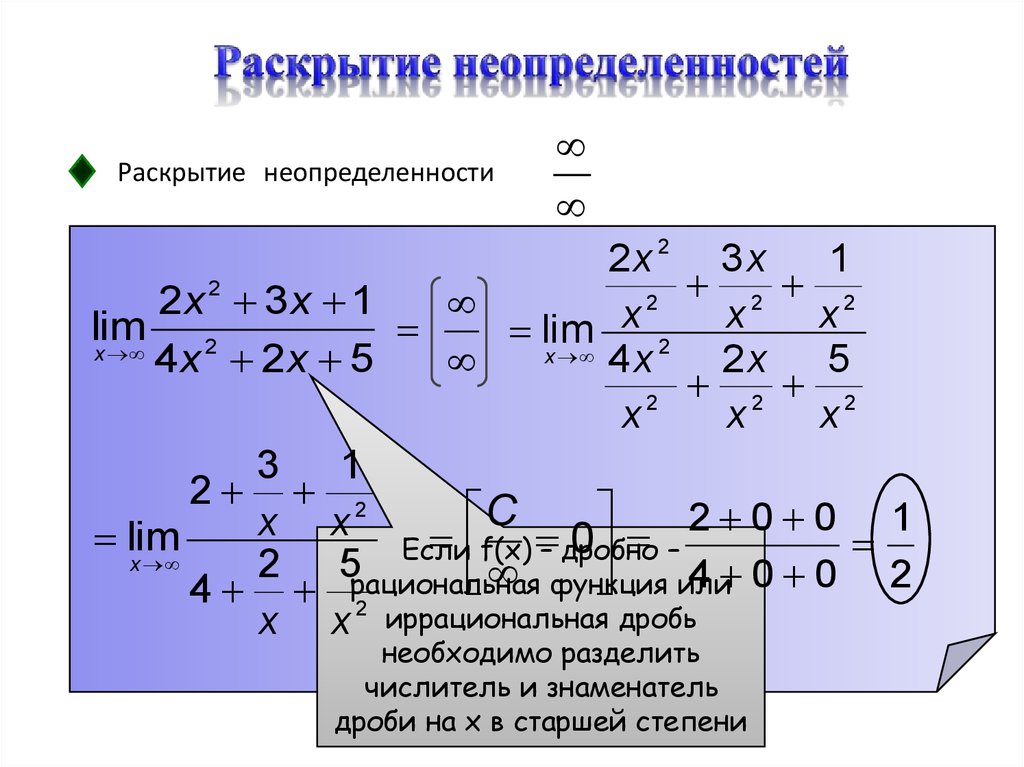
30. Раскрытие неопределенностей

Раскрытие неопределенности
2x 2 3 x 1
2 2
2
2x 2 3 x 1
x
x
x
lim 2
lim
x
x 4 x 2
2x 5
4 x 2x 5
2 2
2
x
x
x
3 1
2 2
C
2 0 0 1
x
x
lim
f(x) – дробно
0 –
Если
x
2 5рациональная
4 0 0 2
функция
или
4 2
x x иррациональная дробь
необходимо разделить
числитель и знаменатель
дроби на x в старшей степени

31.

32.

0
0

33. Раскрытие неопределенностей

Раскрытие неопределенности
lim x 2 1 x 2 1
x
lim
x
lim
x
x 1 x 1
2
2
2
Умножим и разделим
2
1)
функцию
на
сопряженное
lim
2
x
2
выражение.
x 1 x 1
2
2
0
2
x2 1 x2 1
( x 1) ( x
2
x 1 x 1
2
x 1 x 1
2

34. Упражнения:

x3 1
lim 2
x 1 x 1
x 2 5 x 10
lim
x 5
x 2 25
1 x2
lim
x 0 1 2 x 2
lim 2 x 2 3x 4
x 2
x 3 3x 1
lim
1
x 0
x 4
4 x 3 3x 2
lim
x 0 2 x 2 5
lim
x 4
x 1
x 1
lim 7 x 2 4 x 3 5 x 1
x 1

35.

x 2 x 2
lim 2
x 0 x 5 x 4
2
2x 2x
lim 3
x 0 5 x 4 x 2
3
2
x 3
lim
x 3 x 3 x 3
x 3
lim 2
x 3 x 9
2 x 2 x 15
lim
x 3 3 x 2 5 x 12
x 2 6x 5
lim
x 5
x 2 25
lim
x 6
6 x
3 x 3

36. Упражнения:

3x 7 x3
lim
x 7 x3 3
x3 5
lim 2
x x 3
x 3 3x 2
lim 4
x x 2 x 3 3 x 1
x x2
lim
x 1 x3 x
x4 1
lim
x 1 x x 2
4 x 5 2 x 4 3x 1
lim 3
x x 2 x 2 4 x 2
x2 2x 3
lim 2
x 2 x 3 x 4
3x 3 2 x 2 3x 1
lim
X 4 x 3 x 2 7 x 8
x 3x 2
lim
x
1 3x
3 5x x 2 2 x 1
lim
*
x 4 2,5 x
1 x2
2
2x 4x 5
lim
x
x3 4
2
lim 2
x
x