Похожие презентации:
Показательные неравенства
1. Показательные неравенства
mathvideourok.moy.su2.
Показательными неравенстваминазываются неравенства вида
а
f ( x)
a
g ( x)
, где а 0, а 1
Теорема: Если а>1, то из
неравенства
f ( x)
g ( x)
а
a , следует f ( x) g ( x)
Если 0<а<1, то из неравенства
f ( x)
g ( x)
а
a , следует f ( x) g ( x)
3.
1)22 х 4
64
2
2
2х 4 6
2 х 4
2х 10
х 5
1
2)
3
1
3
2 х 3,5
2 х 3,5
6
так как у 2m возрастает
на D( у ) R
Ответ : 5;
1
<
3
1
<
3
2 х - 3,5 0,5
m
1
2
1
так как у убывает
3
2х 4
на D( у ) R
х 2
Ответ : 2;
4.
3)0,5х 2 3 х
0,53 х 8
х 3х 3х 8 так как у 0,5 убывает
m
2
на D( у ) R
х2 - 6х 8 0
Рассторим функцию z х - 6 х 8
2
квадратичная, график парабола, ветви вверх
Ее нули : х2 - 6 х 8 0
D
9 8 1 0(2к )
4
3 1
х1;2
2
4
х
1
х 4; 2
х ;2 4;
Ответ : ;2 4;
5.
4 3 104) х 1
1
3 1
х
4 3х 10
1
х
3 3 1
п 0
4п 10
3п 1 1
Пусть 3 п, п 0
х
4п 10
а)
1
3п 1
4п 10 3п 1
0
3п 1
п 9
0
3п 1
6.
п 9решим
неравенство
методом
интервала
0
п 9
3п 1
рассмотрим функцию у
3п 1
1
Непрерывная на D( у ) R, кроме п функция
3
Ее нули : х 9
Данные точки разбивают числовую прямую на
промежутки в каждом из которых функция
определена,непрерывна и не обращается в 0,
а значит сохраняет свой знак.
7.
у ( 1) 0у (1) 0
+
-
+
1
n
9
у (10) 0
3
1
Отметим п >0 и получаем п ;9
3
1
п 9
3
0
1
3 3 3
1 x 2
x
2
так как z 3 возрастает на D( z ) R
х
Ответ : 1;2
8.
5)0,04х 26 0, 2х 25 00, 2 26 0, 2 25 0
2х
х
Пусть 0, 2 п, п 0
х
п 0
2
п 26п 25 0
п 26п 25 0
2
Рассмотрим функцию у п 26п 25
2
квадратичная, график парабола, ветви вверх
Ее нули : п 26п 25 0
2
D
169 25 144 0(2к )
4
13 12
п1;2
1
п 25;1
9.
п 0п 1;25
1 п 25
х
1 0, 2 25
0
х
2
5 5 5
0 х 2 m
0 1
25
n
так как у 5 возрастает на D( y ) R
2 x 0
Ответ : 2;0
10.
х6)
4
4
х
4 4
1
2
1
х
2
к
так как у= убывает на D ( у R
4
1
Ответ : ;
2
11.
7)2х 2
2
х 3
2
х 4
5
х 1
5
х 2
2 4 2 8 2 16 5 5 5 25
х
х
2 (4 8 16) 5 (5 25)
х
х
х
х
х
20 2 20 5 / : ( 20)
х
х
2 5 / :5 0
х
x
2
1
5
m
х
х
x
2 2
5 5
x 0
0
2
Так как у убывает на D ( у ) R
5
Ответ : (0; )
12.
х 18) х 3 3 0
2
х
х
х 3 3 3 0
х
2
3 ( х 3) 0
Решим неравенство методом
интервала
Рассмотрим функцию у 3х ( х 2 3) непрерывная
2
х
Ее нулих : 3 ( х 2 3) 0
3 0; х 3 0
х
2
на D( y ) R функция.
корней нет
х 3
Данные точки разбивают числовую прямую на
промежутки в каждом из которых функция
определена,непрерывна и не обращается в 0,
а значит сохраняет свой знак.
13.
у ( 10) 0у (10) 0
у (0) 0
-
+
3
+
3
х 3; 3
Ответ : 3; 3
х
14.
9 х 279)
0
2х 4
Решим неравенство методом
интервала
x
9 27
Рассмотрим функцию у
непрерывная
2x 4
на D( y ) R, кроме х 2 функция.
Ее нули : 9 27 0
х
9 27
2х
3
3 3
2х 3
m
Так как z 3 монотонна D( y) R
х 1,5
х
15.
Данные точки разбивают числовую прямую напромежутки в каждом из которых функция
определена,непрерывна и не обращается в 0,
а значит сохраняет свой знак.
у (0) 0
+
y (1, 7) 0
1,5
2
+
х
у (3) 0
х ;1,5 2;
Ответ : ;1,5 2;




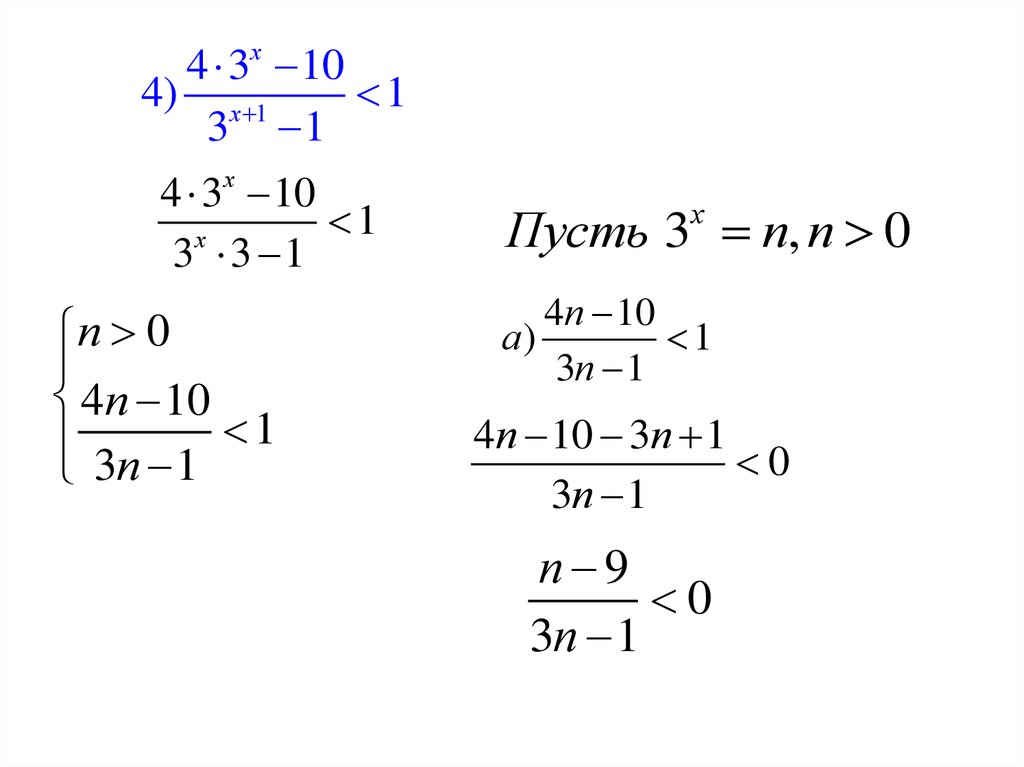










 Математика
Математика








