Похожие презентации:
Поверхности
1. Поверхности
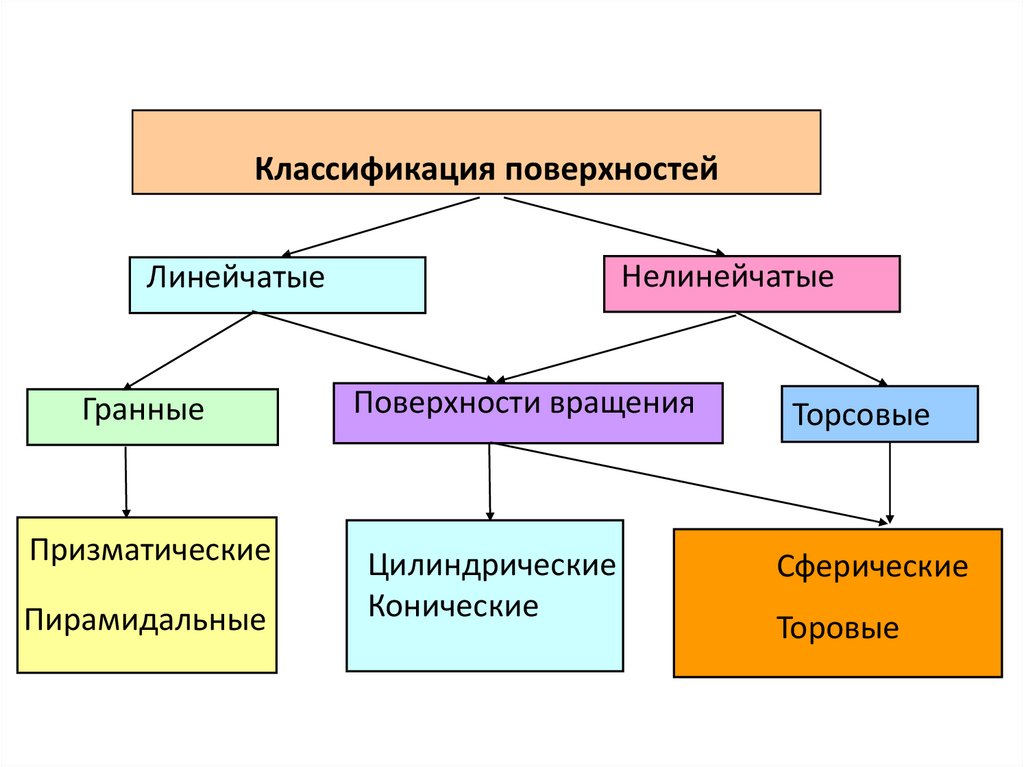
2. Классификация поверхностей
НелинейчатыеЛинейчатые
Гранные
Призматические
Пирамидальные
Поверхности вращения
Цилиндрические
Конические
Торсовые
Сферические
Торовые
3.
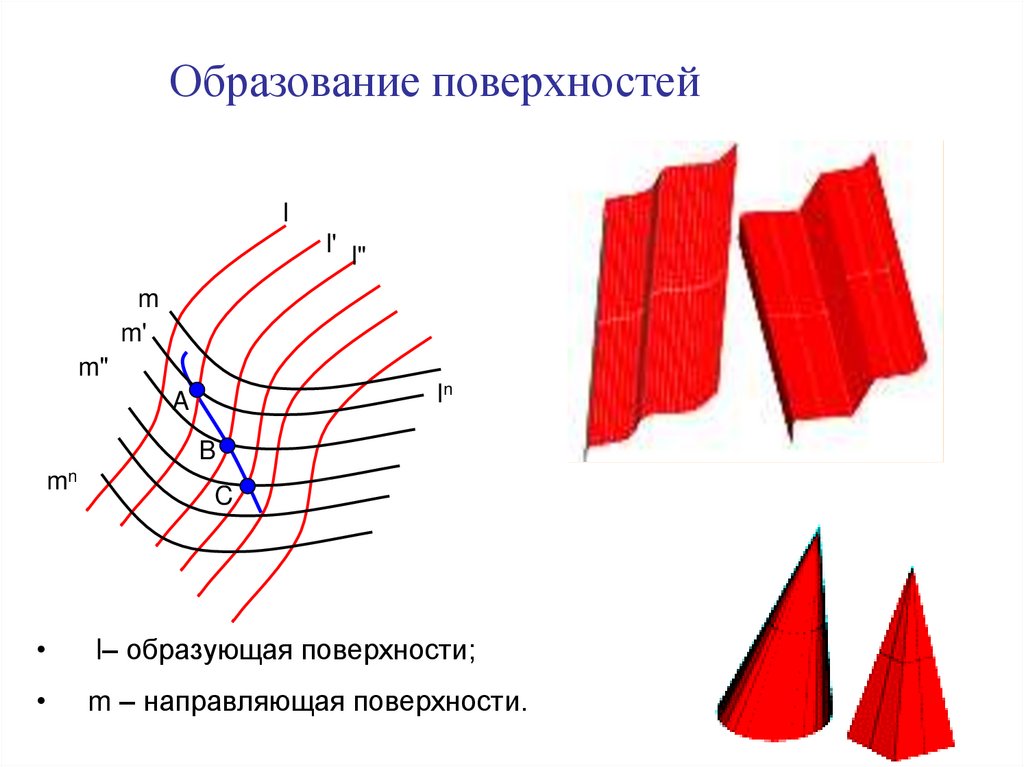
Образование поверхностейl
l' l"
m
m'
m"
ln
A
B
mn
C
l– образующая поверхности;
m – направляющая поверхности.
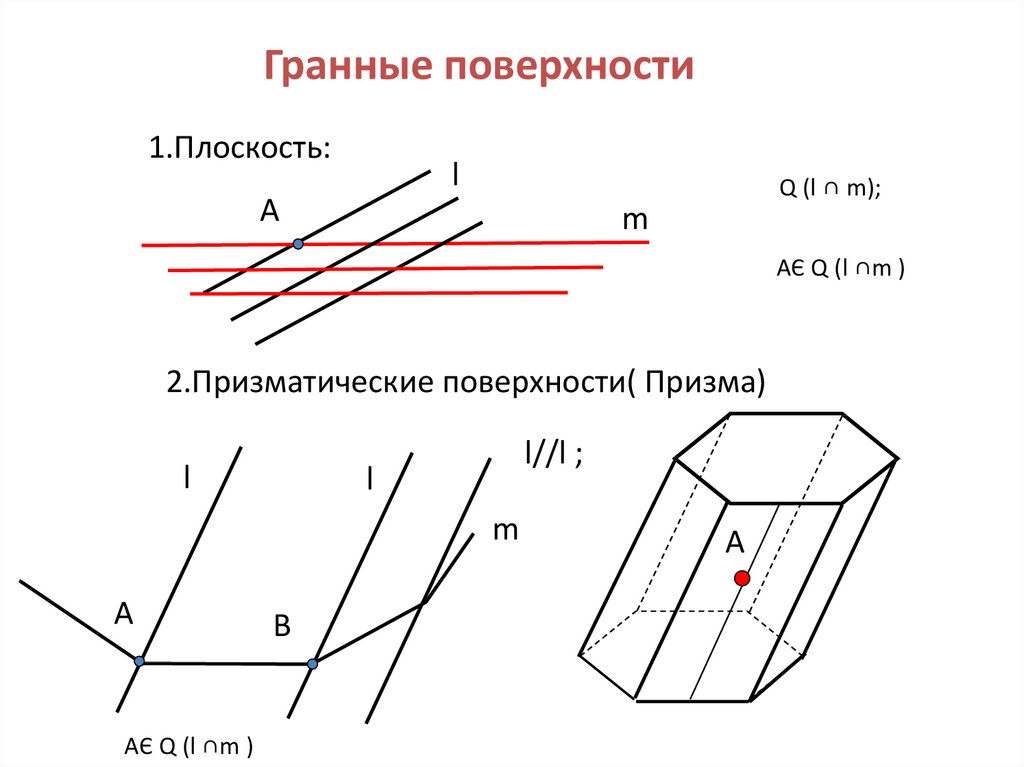
4. Гранные поверхности
1.Плоскость:l
Q (l ∩ m);
A
m
AЄ Q (l ∩m )
2.Призматические поверхности( Призма)
l
l//l ;
l
m
A
AЄ Q (l ∩m )
B
А
5.
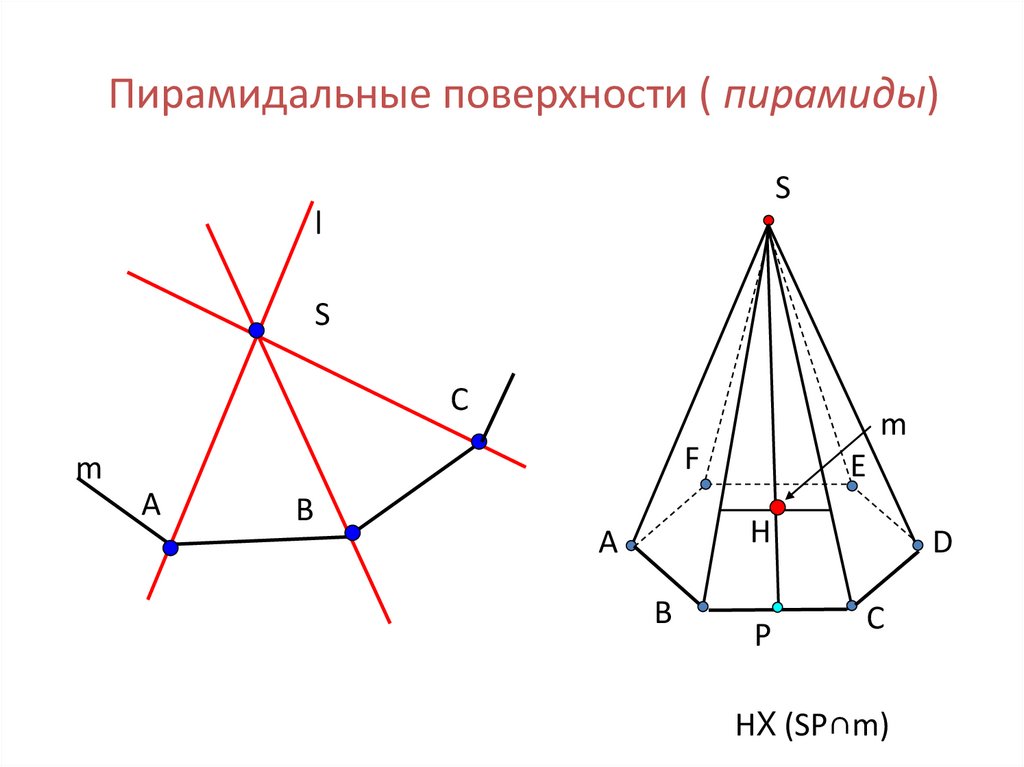
Пирамидальные поверхности ( пирамиды)S
l
S
C
m
F
m
A
B
E
Н
A
B
Р
D
C
HX (SP∩m)
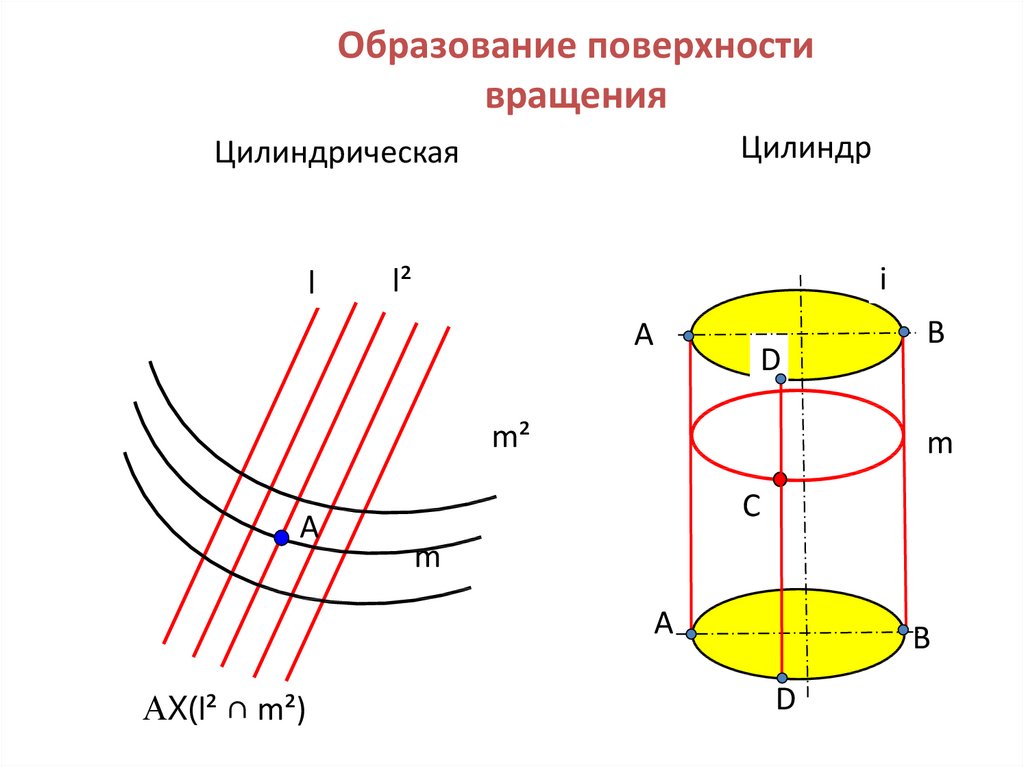
6. Образование поверхности вращения
ЦилиндрЦилиндрическая
l
i
l²
А
D
m²
A
m
С
m
А
AX(l² ∩ m²)
В
В
D
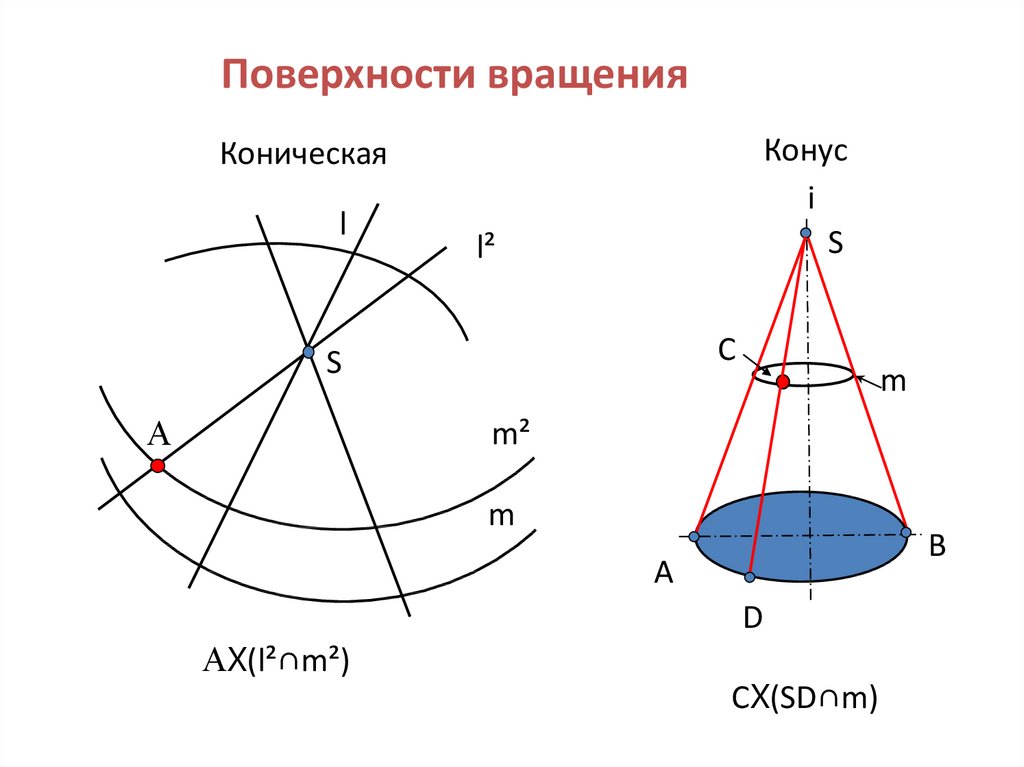
7. Поверхности вращения
Конусi
S
Коническая
l
l²
С
S
A
m
m²
m
В
А
D
AX(l²∩m²)
СX(SD∩m)
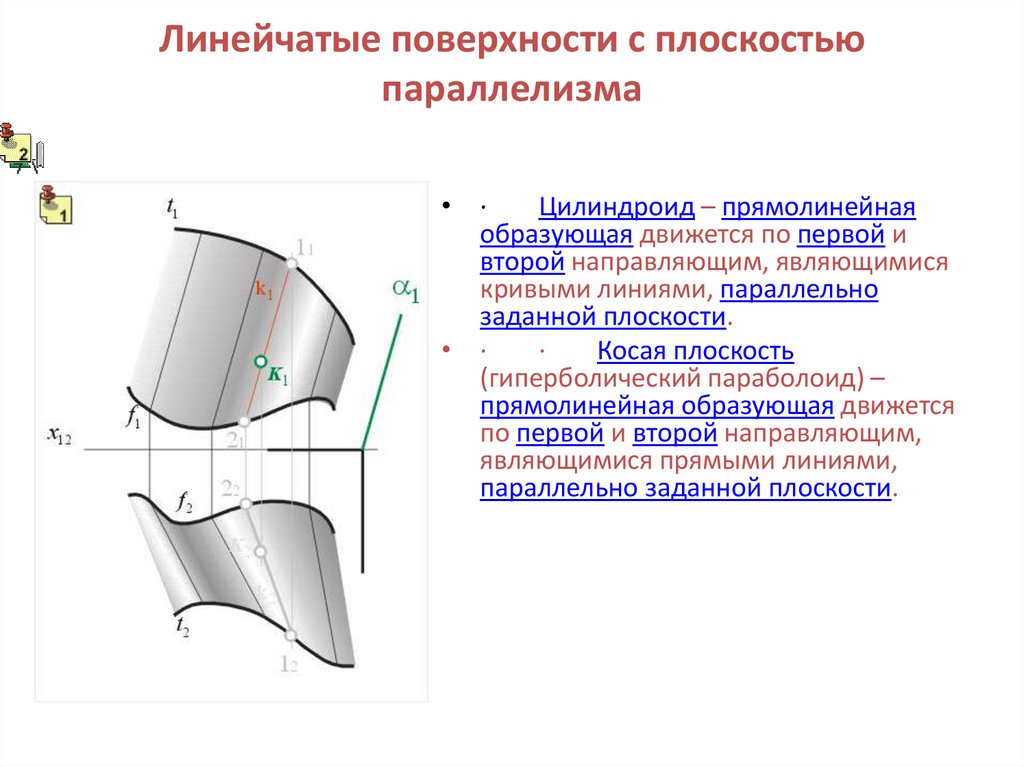
8. Линейчатые поверхности с плоскостью параллелизма
• ·Цилиндроид – прямолинейная
образующая движется по первой и
второй направляющим, являющимися
кривыми линиями, параллельно
заданной плоскости.
• ·
·
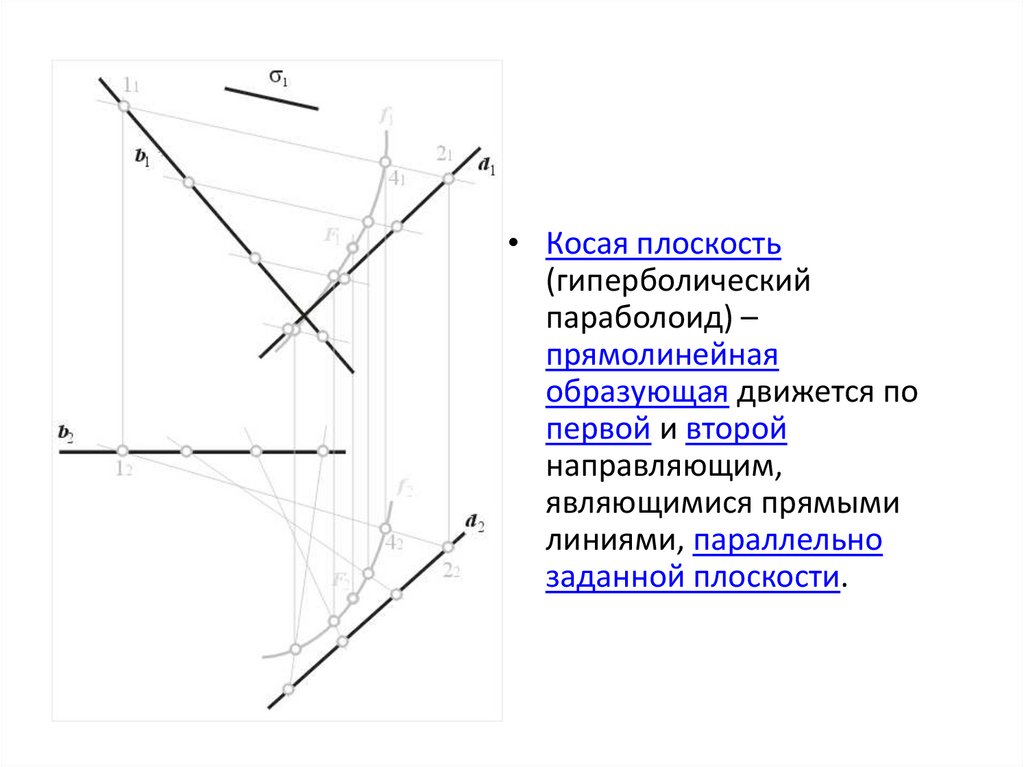
Косая плоскость
(гиперболический параболоид) –
прямолинейная образующая движется
по первой и второй направляющим,
являющимися прямыми линиями,
параллельно заданной плоскости.
9.
• Коноид – прямолинейнаяобразующая движется по
первой и второй
направляющим, одна из
которых прямая линия, а
вторая – кривая линия,
параллельно заданной
плоскости.
10.
• Косая плоскость(гиперболический
параболоид) –
прямолинейная
образующая движется по
первой и второй
направляющим,
являющимися прямыми
линиями, параллельно
заданной плоскости.
11.
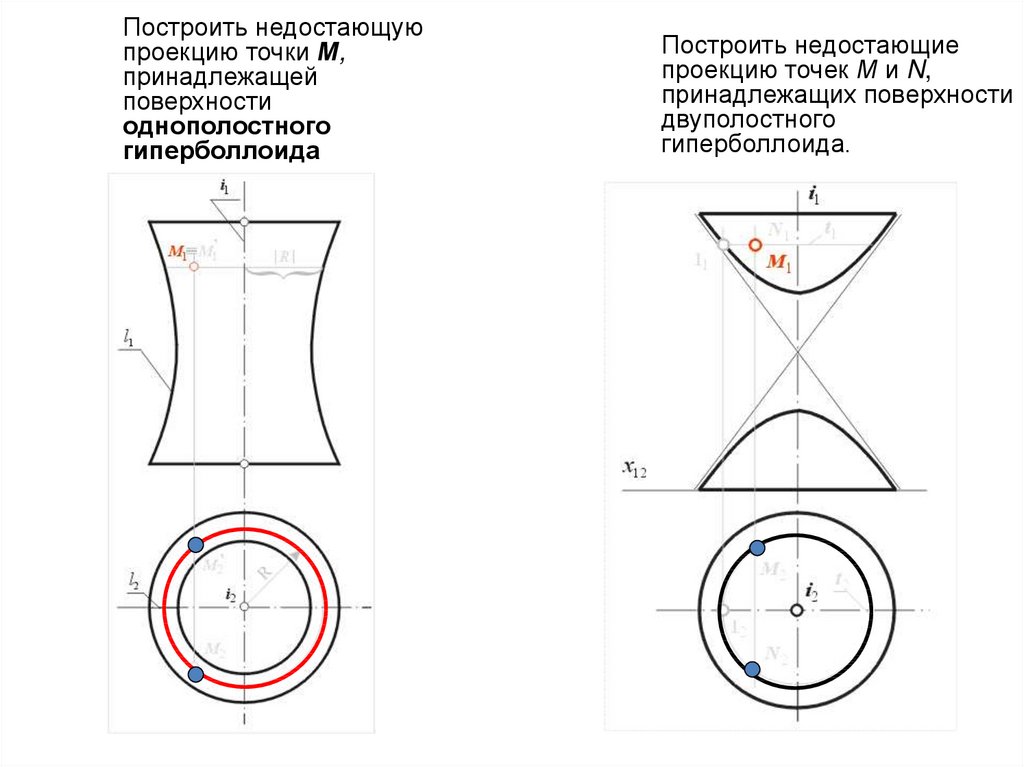
Построить недостающуюпроекцию точки М,
принадлежащей
поверхности
однополостного
гиперболлоида
Построить недостающие
проекцию точек М и N,
принадлежащих поверхности
двуполостного
гиперболлоида.
12.
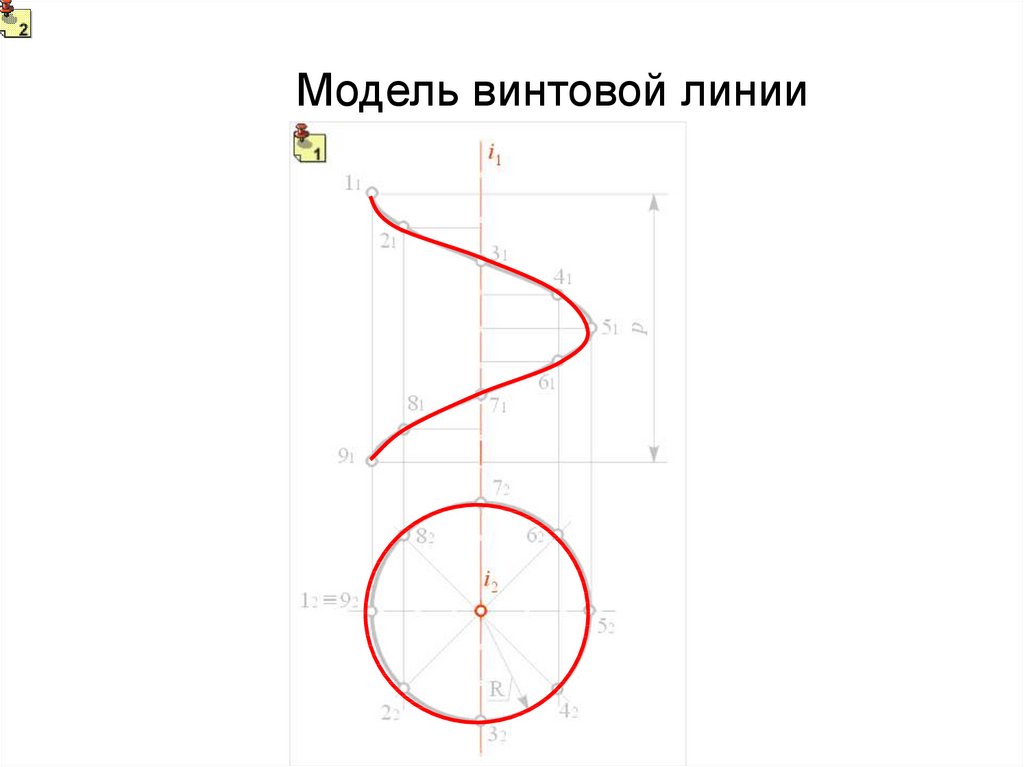
Модель винтовой линии13.
Циклические поверхности14.
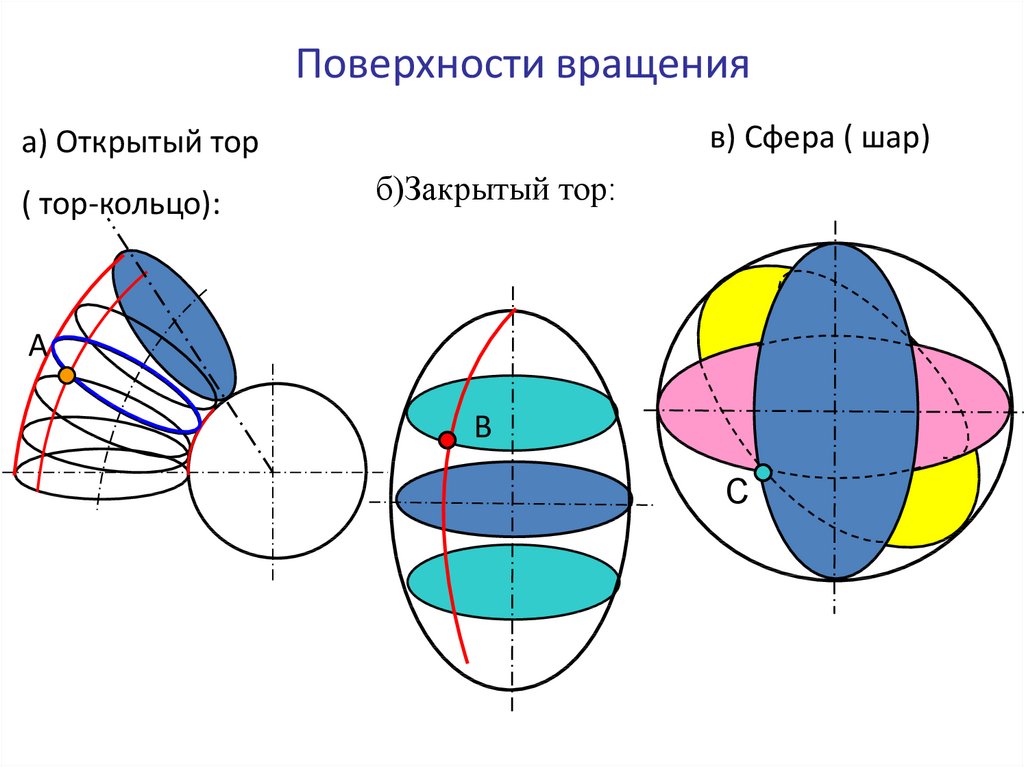
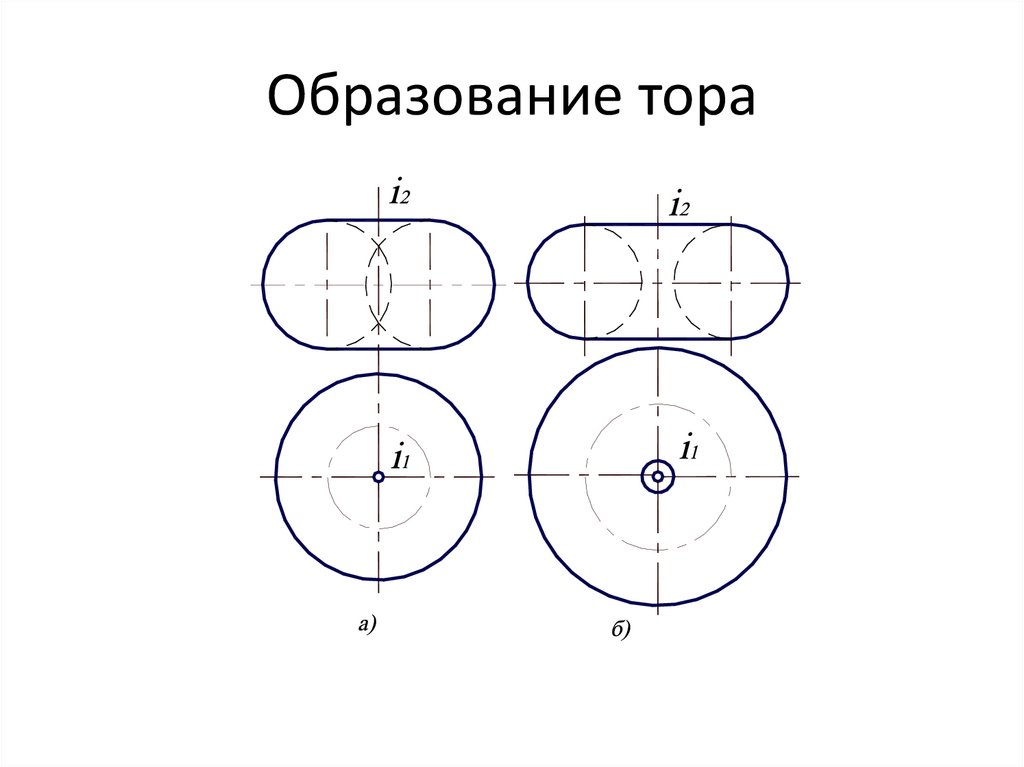
Поверхности вращенияв) Сфера ( шар)
а) Открытый тор
( тор-кольцо):
б)Закрытый тор:
А
В
С
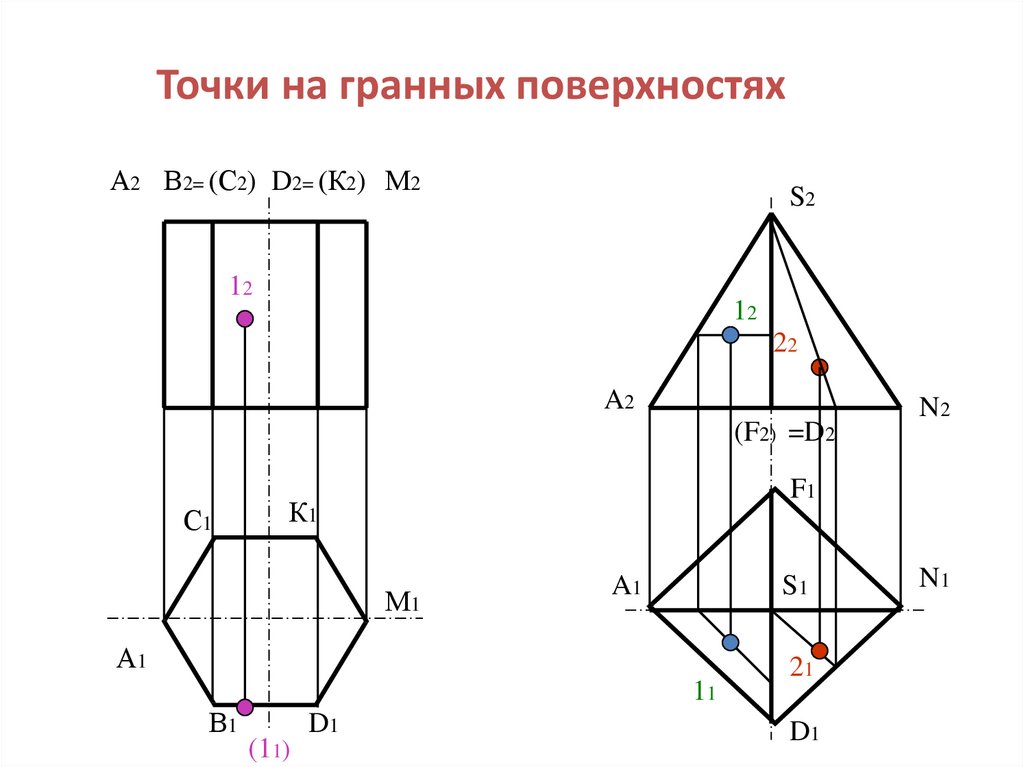
15. Точки на гранных поверхностях
А2 В2= (С2) D2= (К2) М2S2
12
12
22
A2
(F2) =D2
С1
F1
К1
М1
A1
S1
А1
11
В1
(11)
D1
N2
21
D1
N1
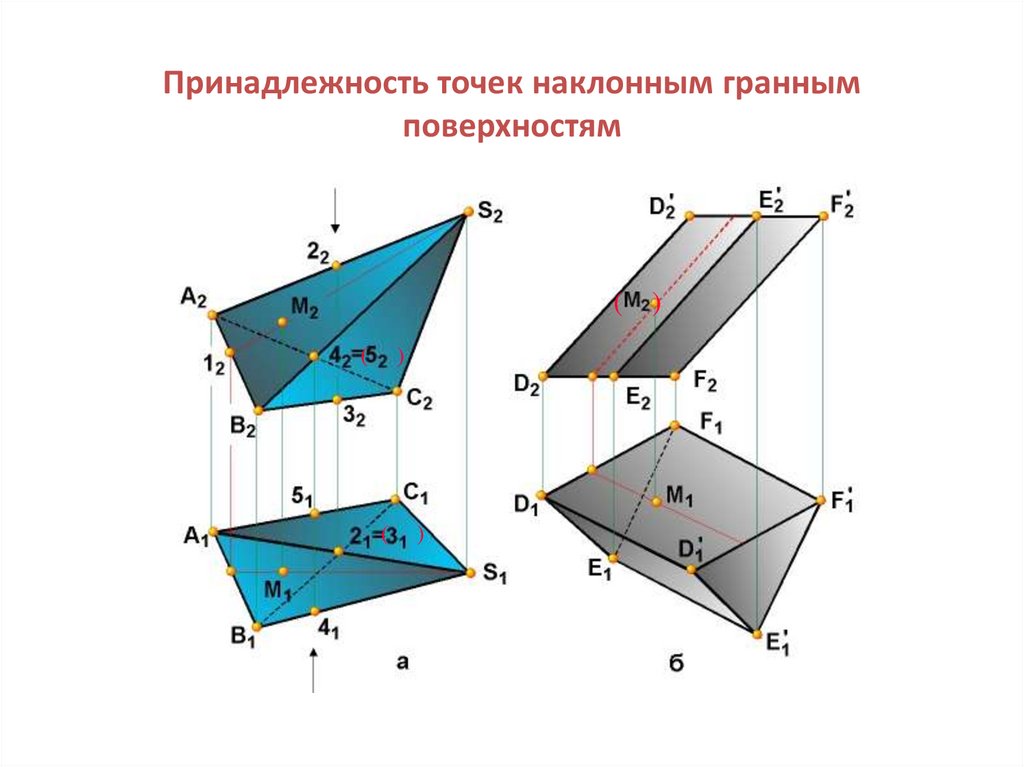
16. Принадлежность точек наклонным гранным поверхностям
( )(
)
(
)
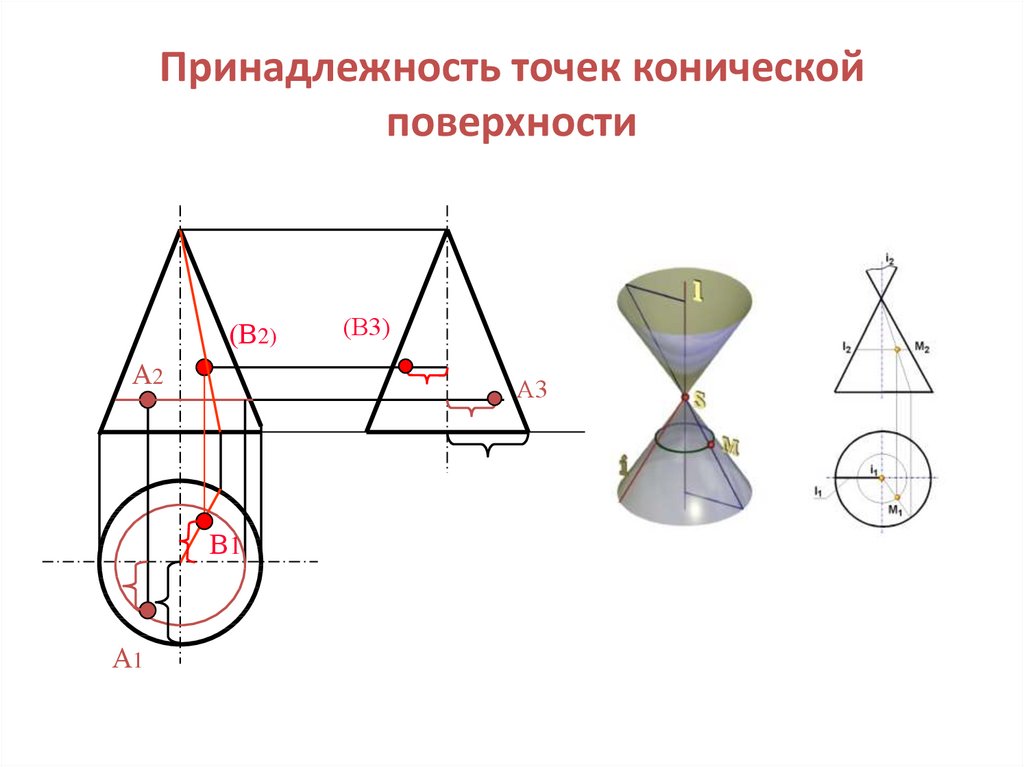
17. Принадлежность точек конической поверхности
(В2)А2
А3
В1
А1
(В3)
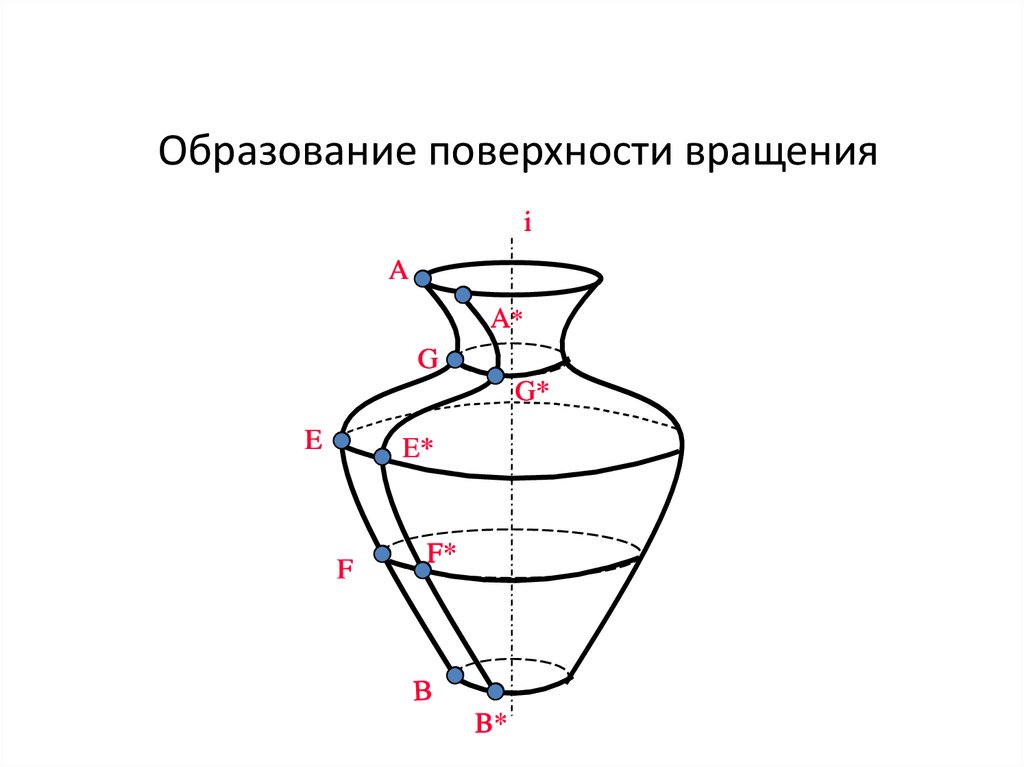
18.
Образование поверхности вращенияi
A
A*
G
G*
E
E*
F
F*
B*
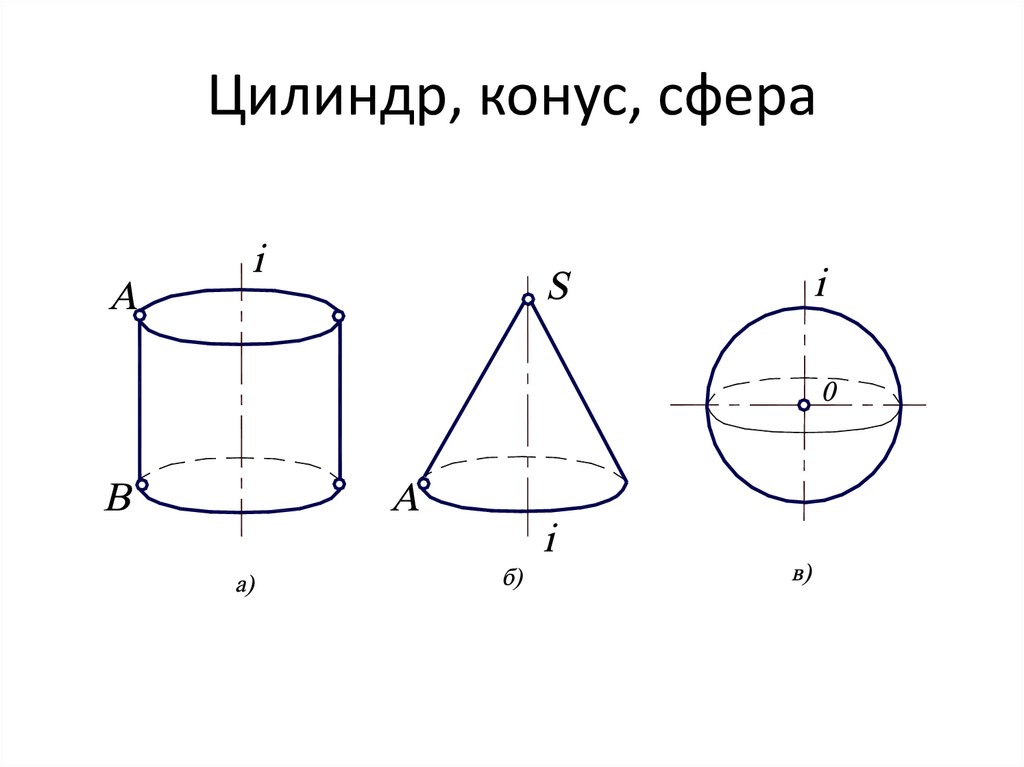
19. Цилиндр, конус, сфера
20. Образование тора
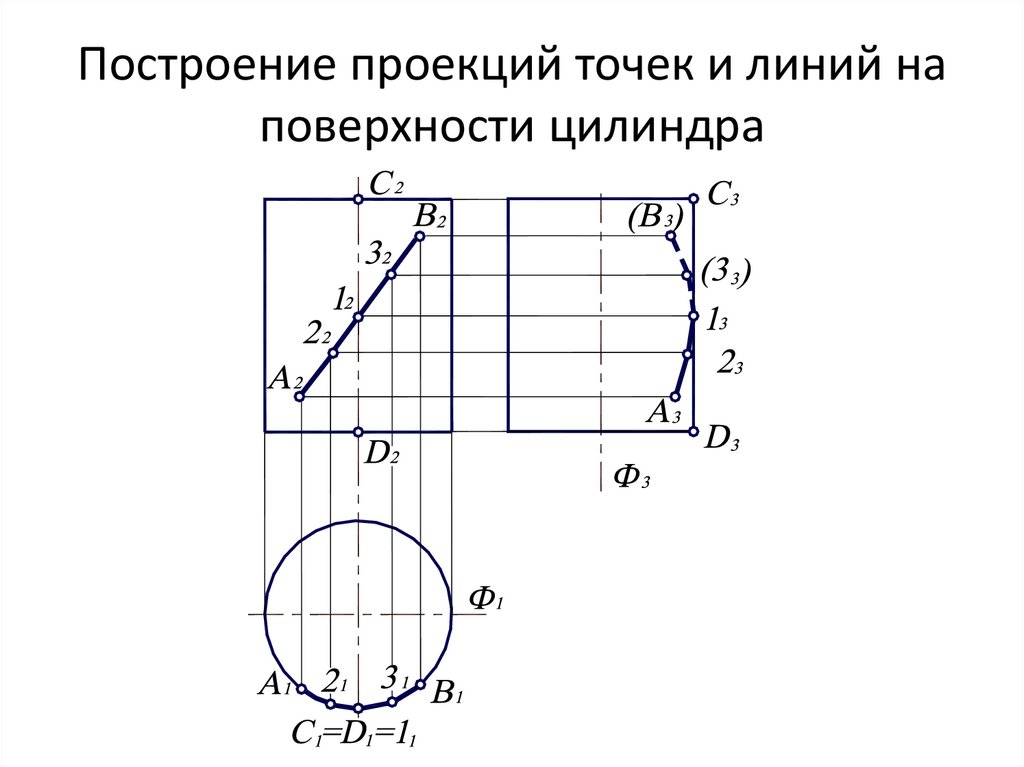
21. Построение проекций точек и линий на поверхности цилиндра
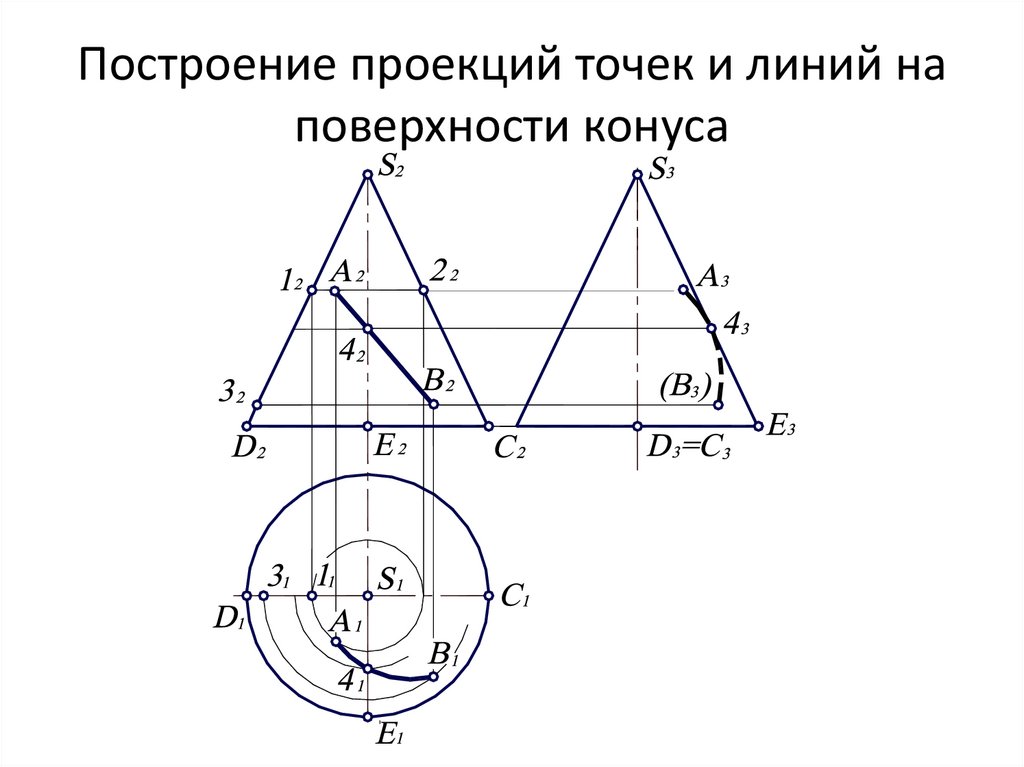
22. Построение проекций точек и линий на поверхности конуса
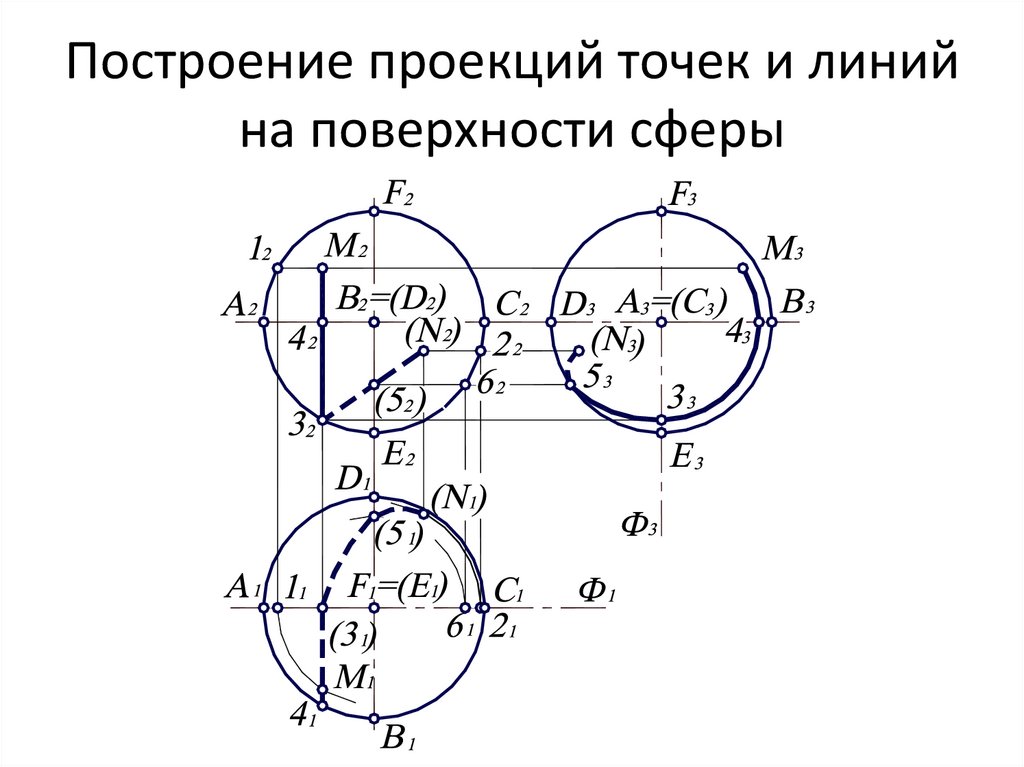
23. Построение проекций точек и линий на поверхности сферы
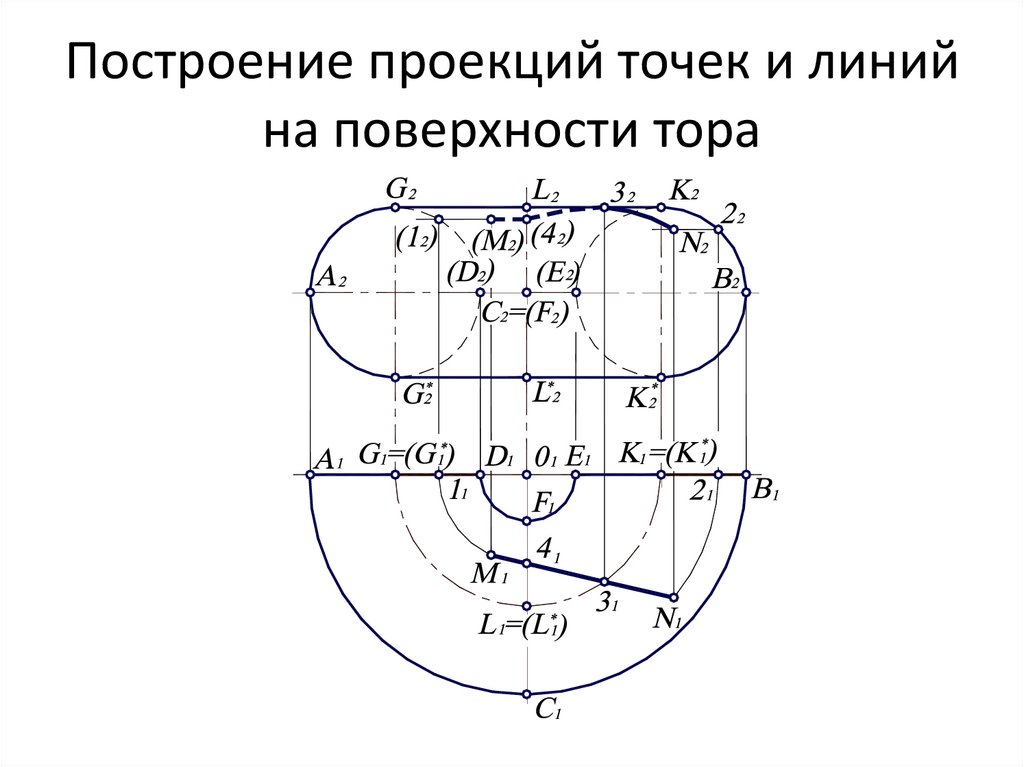
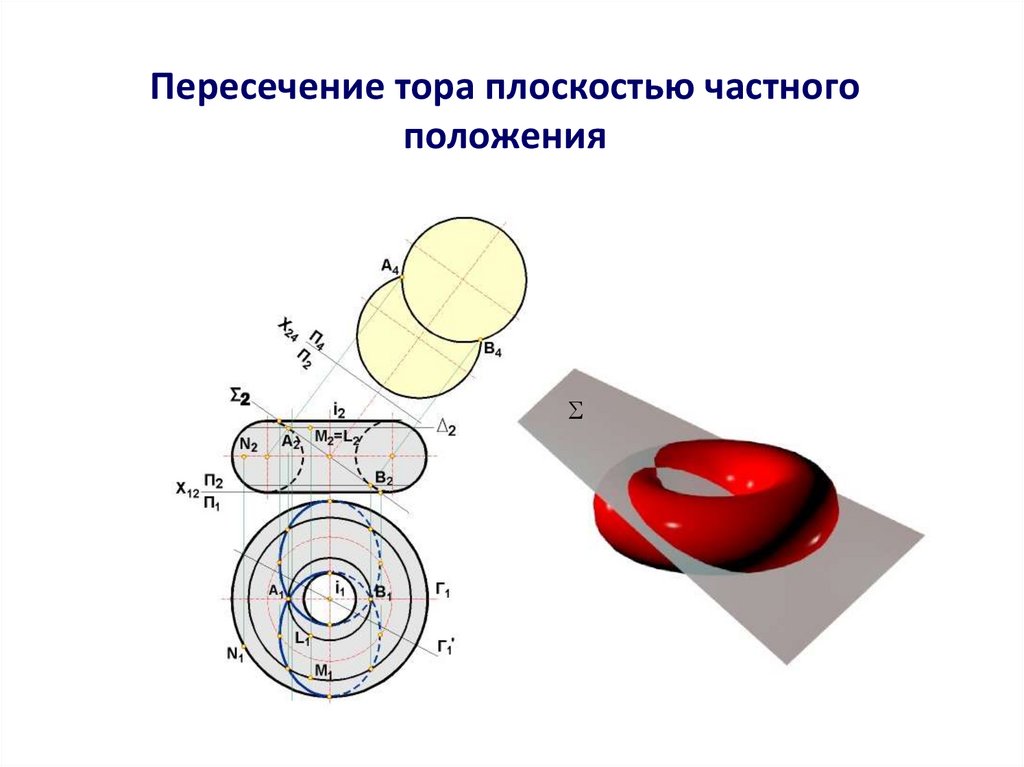
24. Построение проекций точек и линий на поверхности тора
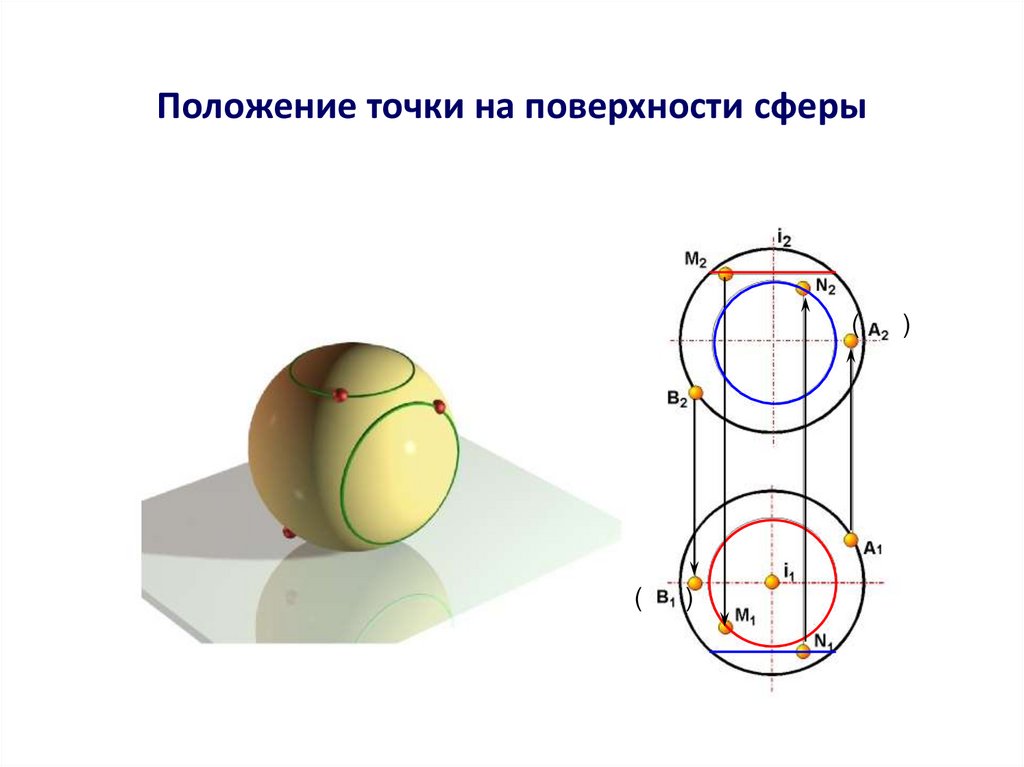
25. Положение точки на поверхности сферы
((
)
)
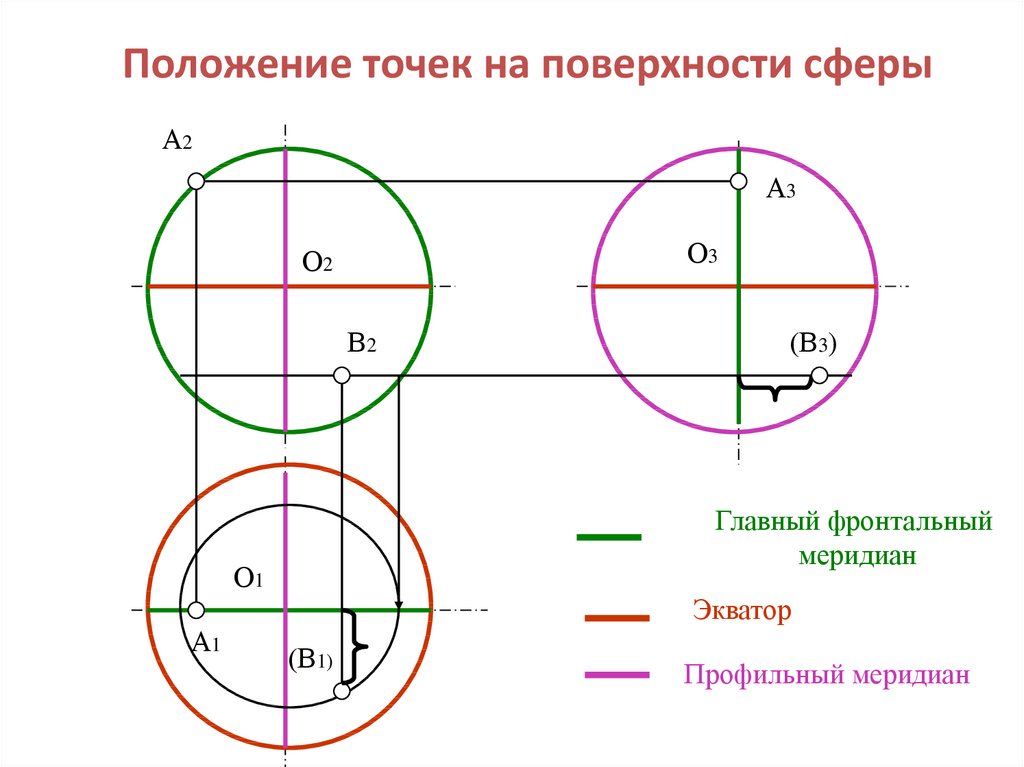
26. Положение точек на поверхности сферы
А2А3
О3
О2
В2
(В3)
Главный фронтальный
меридиан
О1
Экватор
А1
(В1)
Профильный меридиан
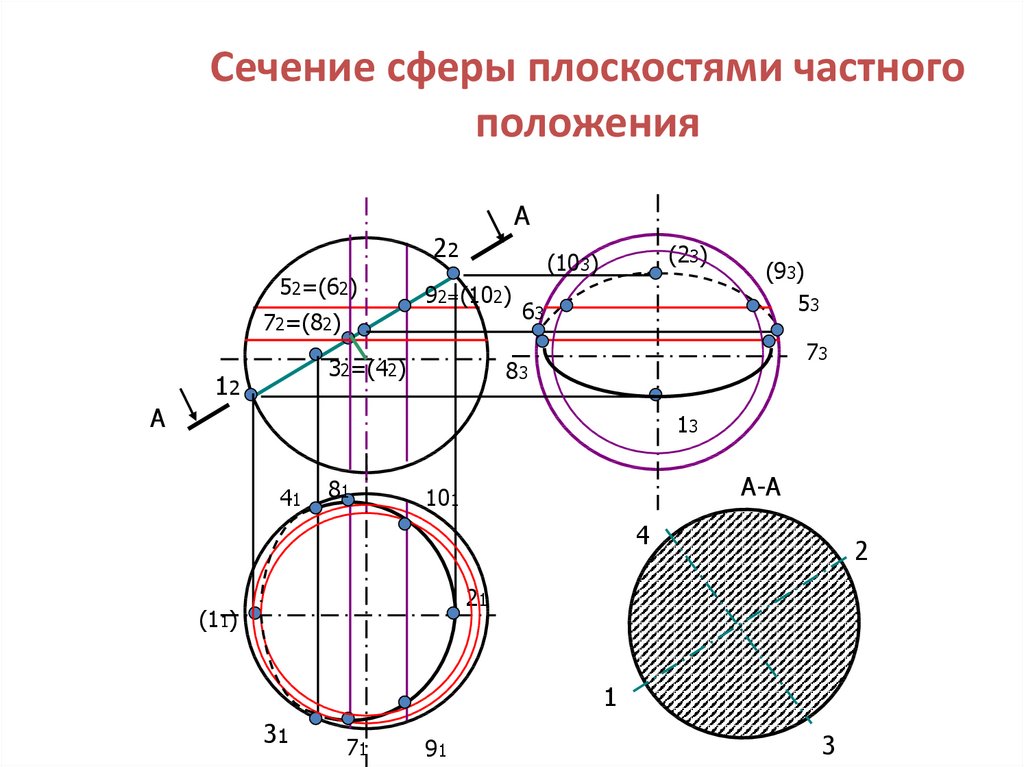
27. Сечение сферы плоскостями частного положения
А22
52=(62)
72=(82)
92=(102)
32=(42)
12
(23)
(103)
63
(93)
53
73
83
А
13
41
81
А-А
101
4
2
21
(11)
1
31
71
91
3
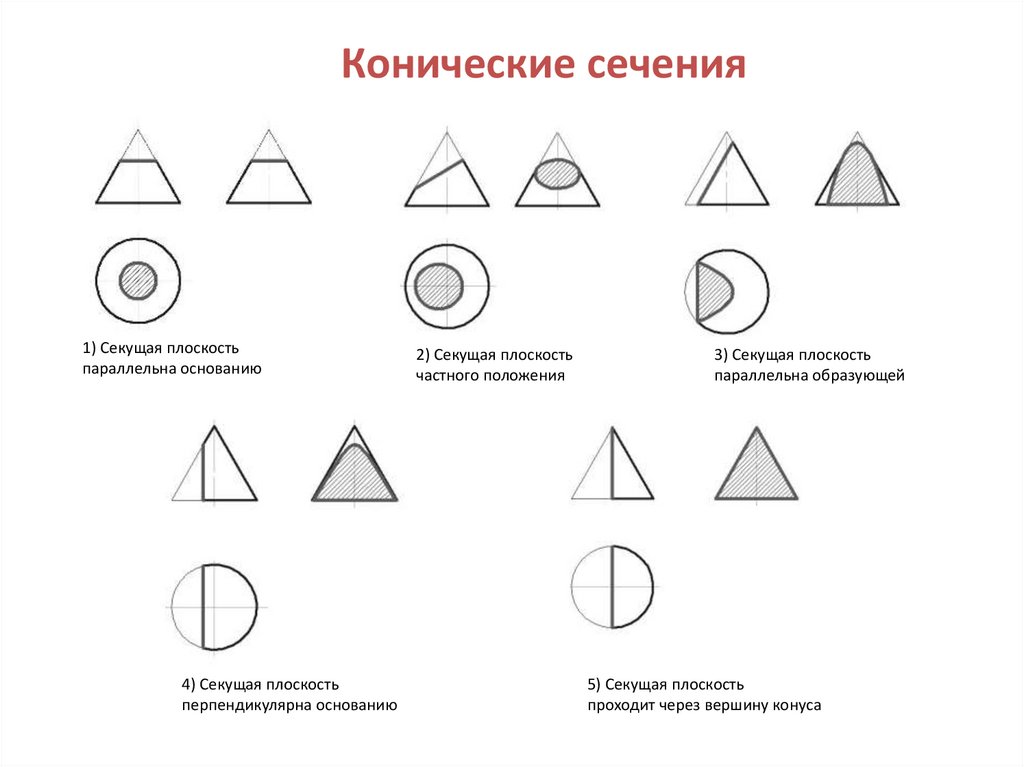
28. Конические сечения
1) Секущая плоскостьпараллельна основанию
4) Секущая плоскость
перпендикулярна основанию
2) Секущая плоскость
частного положения
3) Секущая плоскость
параллельна образующей
5) Секущая плоскость
проходит через вершину конуса
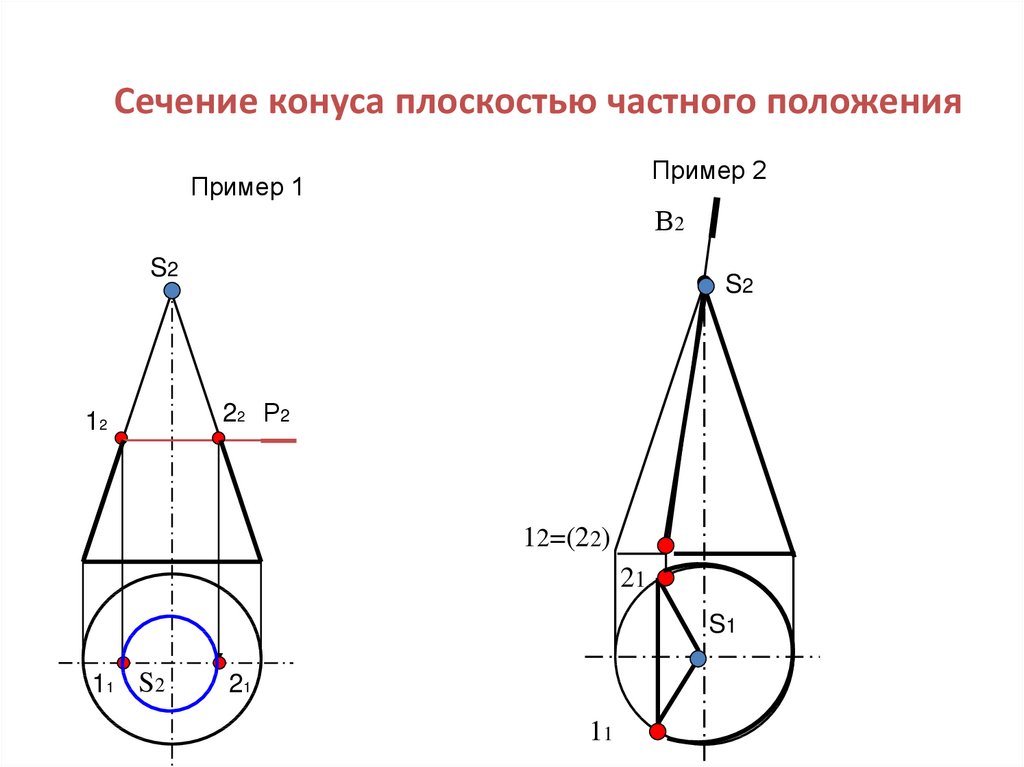
29. Сечение конуса плоскостью частного положения
Пример 2Пример 1
В2
S2
12
S2
22 Р2
12=(22)
21
S1
11 S2
21
11
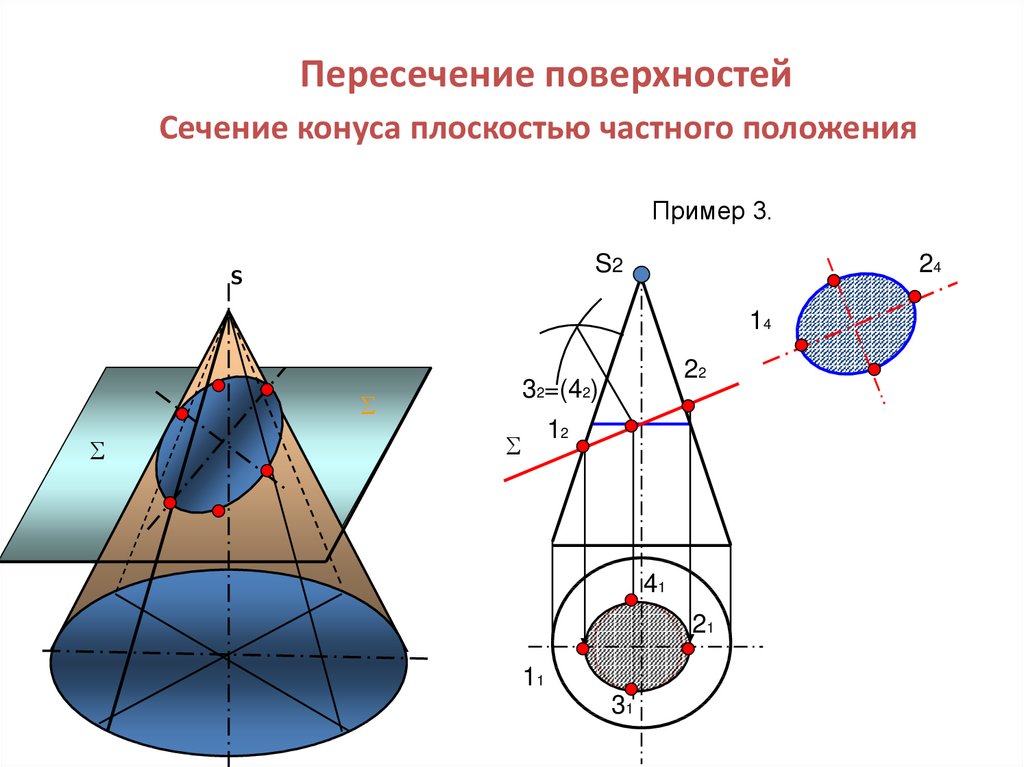
30. Пересечение поверхностей Сечение конуса плоскостью частного положения
Пример 3.S2
s
24
14
22
32=(42)
12
41
21
11
31
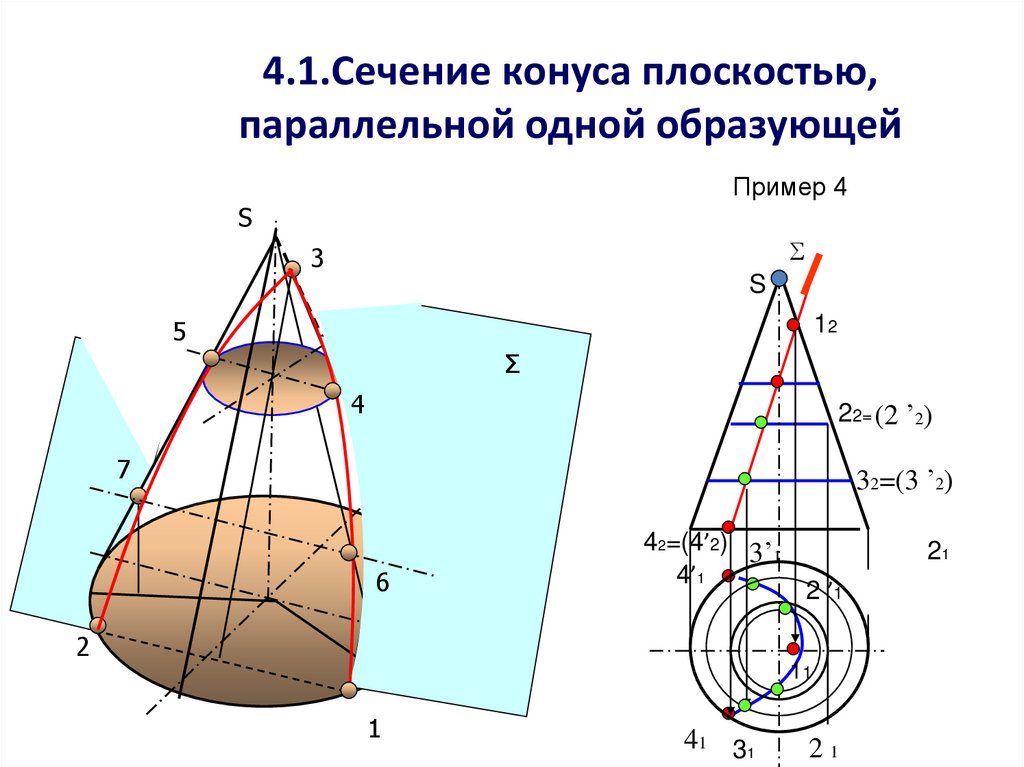
31. 4.1.Сечение конуса плоскостью, параллельной одной образующей
Пример 4S
3
S
12
5
Σ
4
Σ
22= (2 ’2)
7
32=(3 ’2)
6
42=(4’2) 3’1
4’1
21
2 ’1
2
11
1
41 31
21
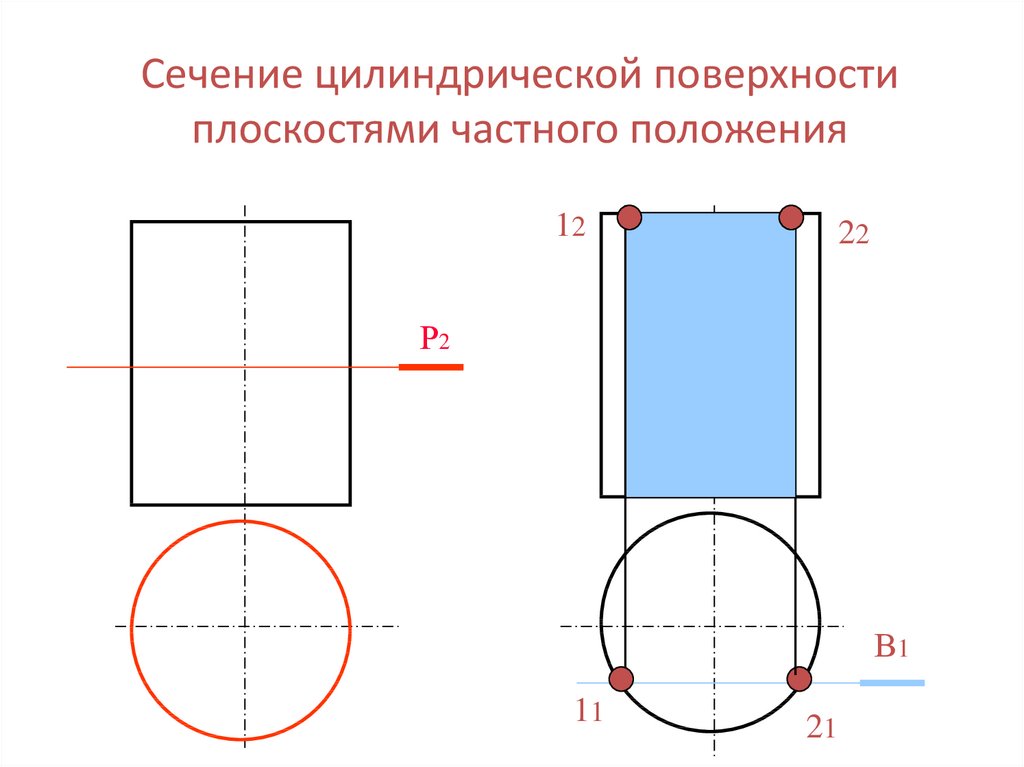
32. Сечение цилиндрической поверхности плоскостями частного положения
1222
Р2
В1
11
21
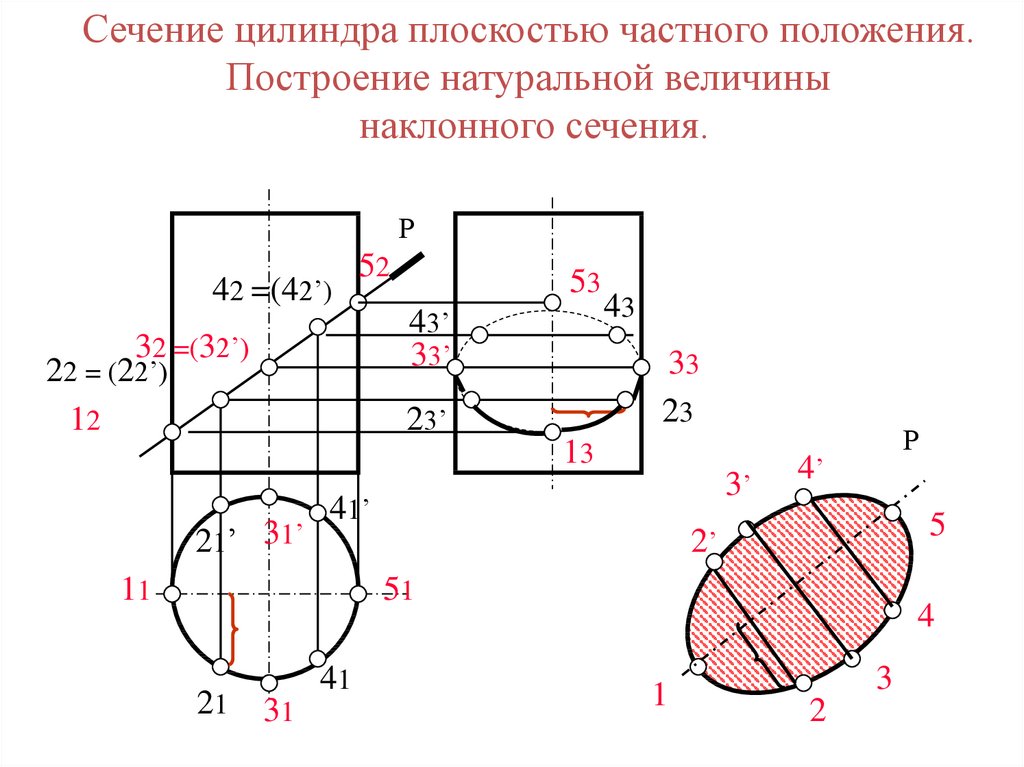
33.
Сечение цилиндра плоскостью частного положения.Построение натуральной величины
наклонного сечения.
Р
42 =(42’)
52
32 =(32’)
22 = (22’)
12
53
43’
33’
43
33
23
23’
13
21’ 31’
3’
41’
11
Р
4’
5
2’
51
21
41
31
4
1
3
2



 Инженерная графика
Инженерная графика








