Похожие презентации:
Матрицы и определители
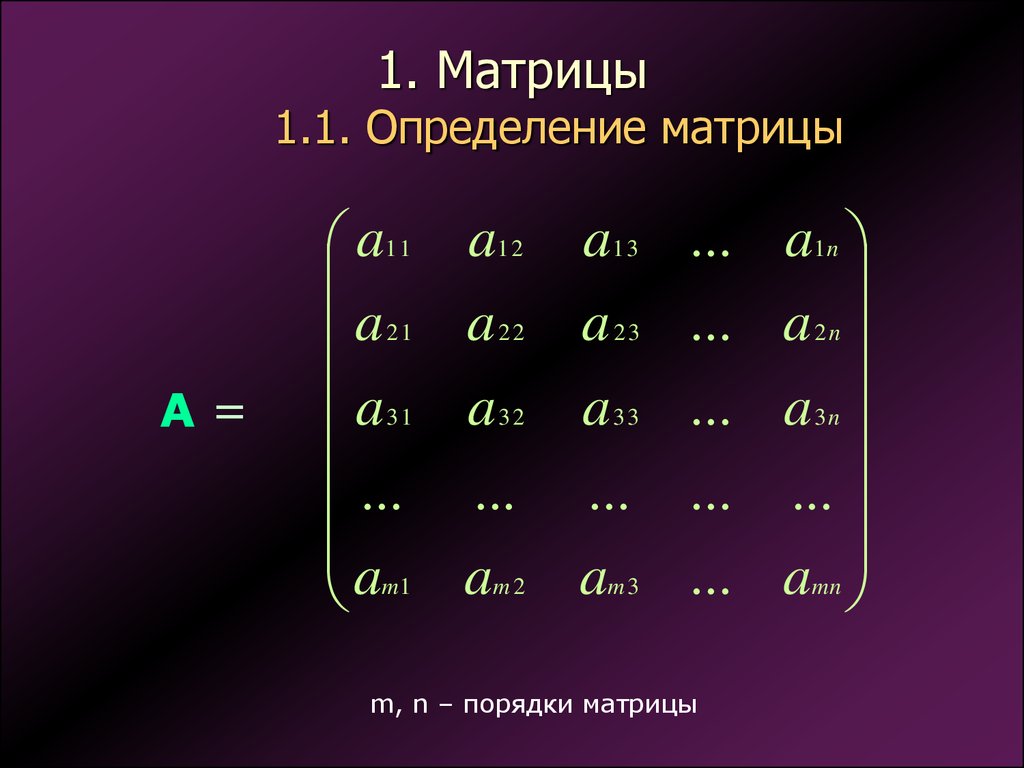
1. 1. Матрицы 1.1. Определение матрицы
A=a1 1
a 21
a31
...
am 1
a1 2
a 22
a32
...
am 2
a1 3 ... a1n
a 2 3 ... a 2 n
a 3 3 ... a 3 n
... ... ...
am 3 ... amn
m, n – порядки матрицы
2. 1.2. Квадратные матрицы
a11a 21
A a 31
...
an1
a12
a 22
a 32
...
an 2
a13
a 23
a 33
...
an 3
...
...
...
...
...
a1 n
a2n
a3n
...
ann
3. 1.4. Транспонирование матриц
a1 1 a 2 1 a 3 1a1 2 a 2 2 a 3 2
T
A a1 3 a 2 3 a 3 3
... ... ...
a1 m a 2 m a 3 m
... an1
... an 2
... an 3
... ...
... an m
4.
Пример транспонирования1 5 3
1 0 6 3
0
0
10
AT 5 0 7 2
A
6
7
8
3 10 8 7
3 2 7
5. 2. Операции над матрицами 2.1. Матричное сложение
A B Cсij aij bij
2 0 3 2
1 2 2 0 1 2
1 3 9 2
3 1 6 3 3 6
4 2 2 4 4 ( 2) 2 4 2 2
6. 2.2. Умножение матрицы на число
k A Bbij k aij
1 2 3 1 3 2 3 6
3 3 1 3 3 3 ( 1) 9 3
4 2 3 4 3 ( 2) 12 6
7. 2.3. Матричное произведение
A B Cñij aik bkj
k
1 2 2 ( 1) 4 0
1 4 2 0
1 2
4 2
12
7
3
4
(
1
)
0
3
2
(
1
)
(
1
)
3
1
0 1
4 4 ( 2) 0 4 2 ( 2) ( 1) 16 10
4 2
Матрицы должны быть сопряженными!
8. 3. Определители
Определитель – это число, дающеекачественную характеристику
матрицы.
a1 1 a1 2 a1 3
a 21 a 22 a 23
det A a 3 1 a 3 2 a 3 3
... ... ...
am1 am 2 am 3
...
...
...
...
...
a1 n
a2n
a3n
...
amn
9. 3.1. Нахождение определителей 1х1
det A a11 a11det( 5) 5 5
10. 3.2. Нахождение определителей 2х2
det A1
2
3
4
a11 a12
a 21 a 22
a11 a22 a12 a21
1 4 2 3 2
11. 3.3. Нахождение определителей 3х3
a1 1 a1 2 a1 3a 2 1 a 2 2 a 2 3 a11 a 22 a33
a31 a32 a33
a11 a12 a13
a 21 a 22 a 23
a21 a32 a13
a31 a12 a 23
a13 a22 a31
a23 a32 a11
a33 a12 a21
12. 3.4. Миноры и алгебраические дополнения
a1 1 ...... ...
Mij ai1 ...
... ...
am1 ...
a1 j ... a1n
... ... ...
aij ... ain
... ... ...
amj ... amn
Aij ( 1)
i j
Mij
13.
1 2 3A 4 0 5
2 4 6
M 32
1 3
4 5
A32 ( 1)
1 5 3 4 5 12 7
3 2
M 32 ( 1) ( 7) 7
14.
1 2 3det 4 0 5 a12 A12 a 22 A22 a32 A32
2 4 6
2 ( 14) 0 4 7 0
A32 7
M 12
4 5
2 6
4 6 5 2 24 10 14
1 2
A12 ( 1)
M 12 ( 1) 14 14
15. 3.7. Обратная матрица
Обратной матрицей для данной квадратнойматрицы A называется такая матрица A-1,
произведение матрицы A на которую справа и слева
является единичной матрицей:
16. Метод нахождения обратной матрицы
Теорема. Для любой невырожденной квадратнойматрицы
существует обратная, и только одна,
определяемая по формуле:
A1 1 A2 1
A1 2 A2 2
1
1
A
A1 3 A2 3
det A
... ...
A1n A2 n
A3 1
A3 2
A3 3
...
A3 n
... An1
... An 2
... An 3
... ...
... An n











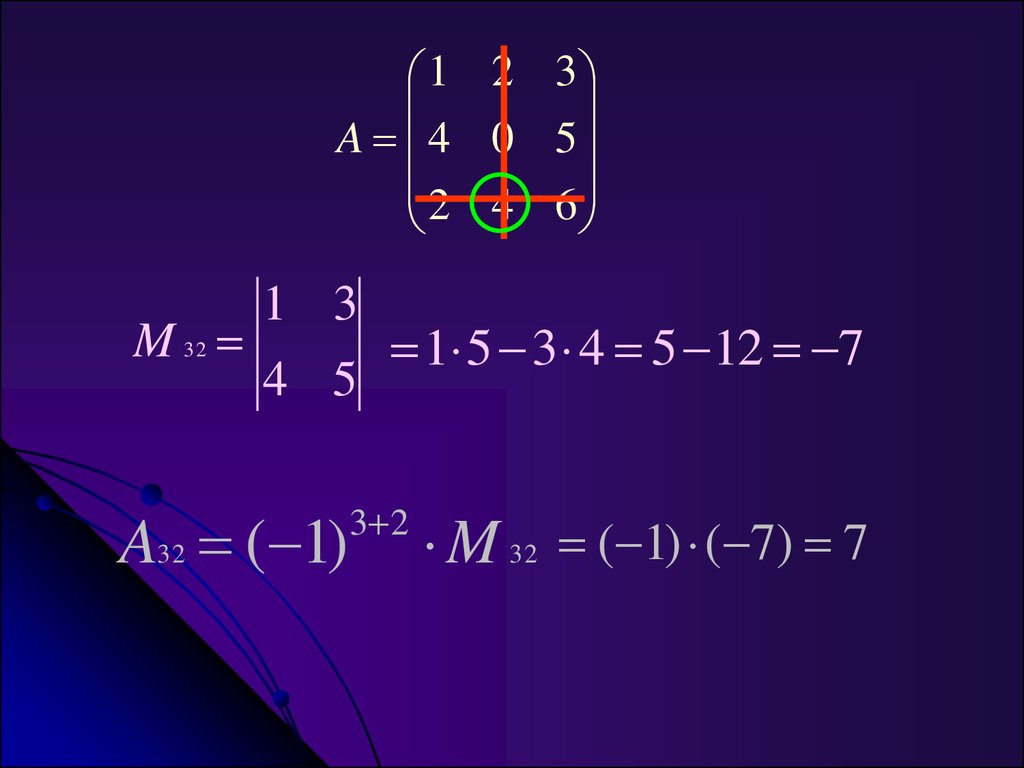



 Математика
Математика








