Логарифмические уравнения

1.

1

2. Свойства логарифма

log a (bc) log a b log a c
b
log a log a b log a c
c
r
log a b r log a b
log a r b
1
log a b
r
log c b
log a b
log c a
а 0;
b 0;
a 1
с 1
с 0

3.

№
a>1
0<a<1
1
D(f) = (0, + ∞)
2
не является ни чётной, ни нечётной;
3
возрастает на (0, + ∞)
убывает на (0, + ∞)
4
не ограничена сверху, не ограничена снизу
5
не имеет ни наибольшего, ни наименьшего значений
6
непрерывна
7
E(f) = (- ∞, + ∞)
8
9
выпукла вверх
выпукла вниз
точка пересечения графика функции с осью Ох (1,0).
3

4.

Уравнения, содержащие неизвестное
под знаком логарифма или в
основании логарифма называются
логарифмическими уравнениями.
4

5.

log a f ( x) log a g ( x)
log a f ( x) g ( x)
f ( x) a
f ( x) g ( x)
f ( x) 0
g ( x)
g ( x) 0
log a ( f ( x))
2n
g ( x)
2n log a f ( x) g ( x)

6.

По определению логарифма;
Метод потенцирования;
Метод введения новой переменной;
Метод логарифмирования;
Метод приведения к одному
основанию;
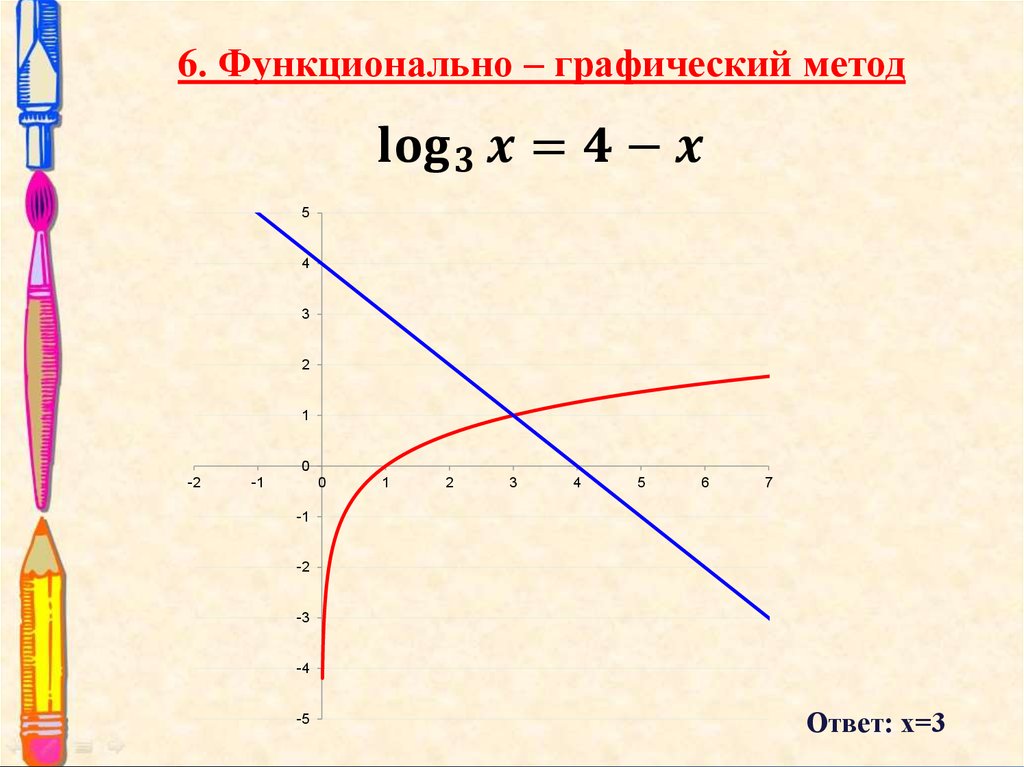
Функционально-графический метод.
6

7.

Методы решения
ЛУ:
1.Применение
определения логарифма
Вид уравнения
log a f ( x) b
2.Введение
новой переменной
log f ( x) b log a f ( x) c 0
3. Приведение к одному и
тому же основанию
log a f ( x) log с g ( x)
4. Метод потенцирования
5 Метод логарифмирования
2
a
log a f ( x) log a g ( x)
обеих частей уравнения
loq a x
х
6. Функциональнографический метод
log a f ( x) g ( x)
с
n

8.

Методы решения логарифмических уравнений
1. По определению логарифма.
На основе определения логарифма решаются уравнения, в которых
по данным основанию и числу определяются логарифм, по
данному логарифму и основанию определяется число и по данному
числу и логарифму определяется основание.