Похожие презентации:
Первообразная. Неопределенный интеграл
1. Первообразная. Неопределенный интеграл.
2. Основные вопросы:
Определение первообразной. Основноесвойство первообразной.
Понятие неопределенного интеграла.
Основные формулы интегрирования.
Непосредственное интегрирование (метод
разложения).
Этапы интегрирования функций методом
подстановки (замены переменной).
Интегрирование некоторых
тригонометрических функций
3. Определение первообразной. Основное свойство первообразной.
Функция F(x) называетсяпервообразной для функции f(x) на
интервале X=(a,b) (конечном или
бесконечном), если в каждой точке этого
интервала f(x) является производной для
F(x), т.е.
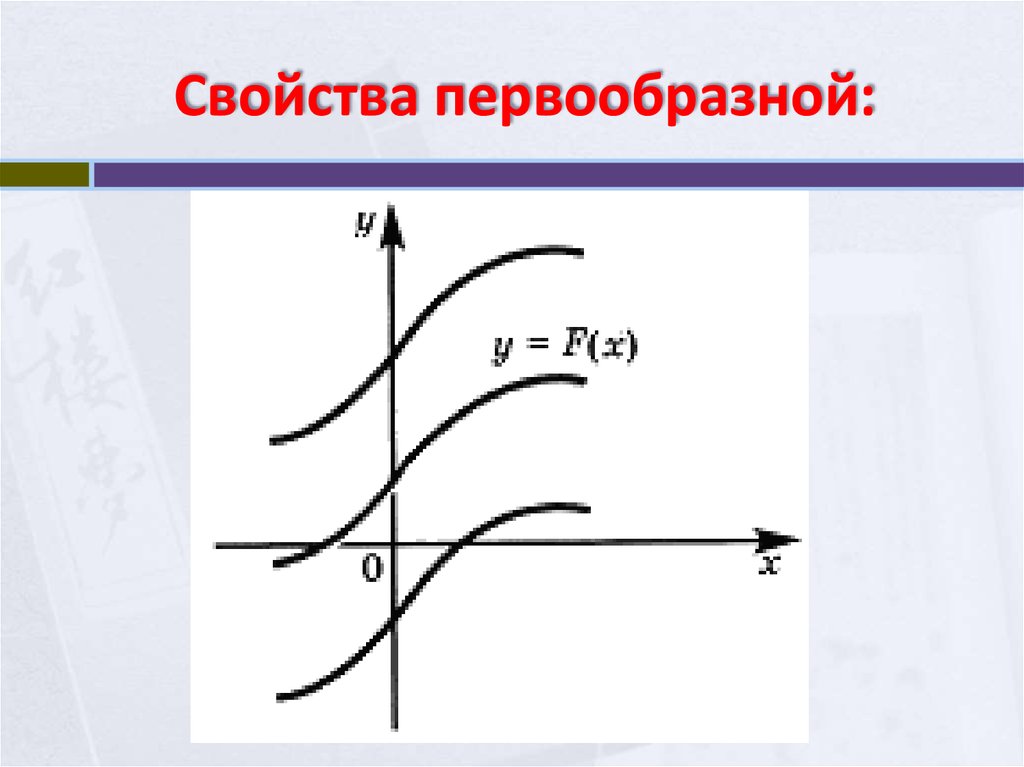
4. Свойства первообразной:
1. Если функция F(x) - первообразная дляфункции f(x) на интервале X, то функция f(x) +
C, где C - произвольная постоянная, тоже будет
первообразной для f(x) на этом интервале.
Этому свойству первообразных можно придать
геометрический смысл: графики любых 2-х
первообразных для функции f(x) получаются друг от
друга параллельным переносом вдоль оси Оу
5. Свойства первообразной:
6. Свойства первообразной:
2. Если функция F(x) - некоторая первообразнаядля функции f(x) на интервале X=(a,b), то
любая другая первообразная F1(x) может
быть представлена в виде
F1(x) = F(x) + C, где C - постоянная на X функция.
7. Свойства первообразной:
3. Для любой первообразной F(x)выполняется равенство dF(x) = f(x) dx.
Из этих свойств следует, что если F(x) - некоторая
первообразная функции f(x) на интервале X, то всё
множество первообразных функции f(x) (т.е.
функций, имеющих производную f(x) и дифференциал
f(x) dx) на этом интервале описывается выражением
F(x) + C, где C - произвольная постоянная.
8. Таблица первообразных
9. Понятие неопределенного интеграла. Основные формулы интегрирования
Множество первообразных функции f(x)называется неопределённым интегралом от этой
функции и обозначается символом
10.
5x
x dx 5 C
4
поскольку функция
x 5 - первообразная для функции х4.
5
Процесс нахождения неопределенного интеграла
функции называется интегрированием этой функции.
11. Свойства неопределенного интеграла:
1. Производная неопределенногоинтеграла равна подынтегральной
функции:
( f ( x)dx) f ( x)
Это свойство считается очень важным, его используют
для проверки правильности вычисления интеграла.
12. Свойства неопределенного интеграла:
2. Дифференциал от неопределенногоинтеграла равен подынтегральному
выражению:
13. Свойства неопределенного интеграла:
3. Неопределенный интеграл отдифференциала функции равен этой
функции плюс произвольная
постоянная:
14. Свойства неопределенного интеграла:
4.Постоянный множитель можновыносить за знак неопределенного
интеграла:
kf
(
x
)
dx
k
f
(
x
)
dx
15. Свойства неопределенного интеграла:
5.Неопределенный интеграл от суммы 2-хфункций равен сумме неопределенных
интегралов от этих функций:
16. Таблица неопределенных интегралов:
17. Таблица неопределенных интегралов:
18. Непосредственное интегрирование (метод разложения).
Непосредственным интегрированиемназывается метод нахождения интегралов,
основанный на использовании таблицы и
основных свойств неопределенных интегралов
Здесь могут представиться следующие случаи:
1. данный интеграл сразу находится по таблице;
2. данный интеграл после применения свойств 4 и 5 сводится к
табличным;
3. данный интеграл после элементарных тождественных
преобразований над подынтегральной функцией и применением
свойств 4 и 5 сводится к табличным.
19.
Проверка:Проверка:
20.
21. Отметим несколько полезных правил для вычисления интегралов.
Если известна первообразная функции, а числа
, т.е.
и
константы, то:
22.
23.
Найти5
(
5
x
3
)
dx
Решение: введем подстановку u = 5x + 3
дифференциал этого выражения:
d (5x + 3) = du
5dx = du, откуда
dx = 1/5 du
Подставив вместо 5х +3 и dx их значения в
данный интеграл, получим:
6
1 5
1 u
1 6
(5x 3) dx 5 u du 5 6 c 30 u c
5
24.
Заменив u его выражением через x, имеем:1
6
(5x 3) dx 30 (5x 3) c
5
Проверка:
1
6
6
d (5 x 3) c (5 x 3) 5 5 dx (5 x 3) 5 dx
30
30
Интеграл найден правильно.
25.
3x
x
1
dx
Решение:
t3 x 1 x t3 1
t 3 x 1
d ( x 1) d (t 3 )
dx 3t dt
2
Заменяя переменную в данном интеграле, имеем:
7
4
t
t
3
2
6
3
3
x
x
1
dx
(
t
1
)
t
3
t
dt
3
(
t
t
)dt 3( c
7 4)
Подставляя вместо t его выражение через x, найдем:
(3 x 1)7 (3 x 1) 4
( x 1) 2 3 x 1 ( x 1) 4 x 1
) c
x x 1 dx 3( 7 4 ) c 3(
7
4
3
( x 1) (4 x 3) 3 x 1 c
28
3
26.
du1
1
sin(5x 3) dx sin u 5 5 cos u c 5 cos(5x 3) c
5x 3 u
d (5 x 3) du
5dx du
du
dx
5
27.
Интегрирование некоторых тригонометрическихфункций.
Интегралы от произведений синусов и
косинусов с разными аргументами, линейно
зависящими от , упрощаются, если
применить тригонометрические формулы
преобразования произведения в сумму:
28.
Вычислим интегралПреобразуем произведение
сумму:
тогда
в
29. Упражнения :
sin 8x cos 3xdxsin 3x sin 2 xdx





























 Математика
Математика








