Похожие презентации:
Проекция вектора перемещения
1. Проекция вектора перемещения
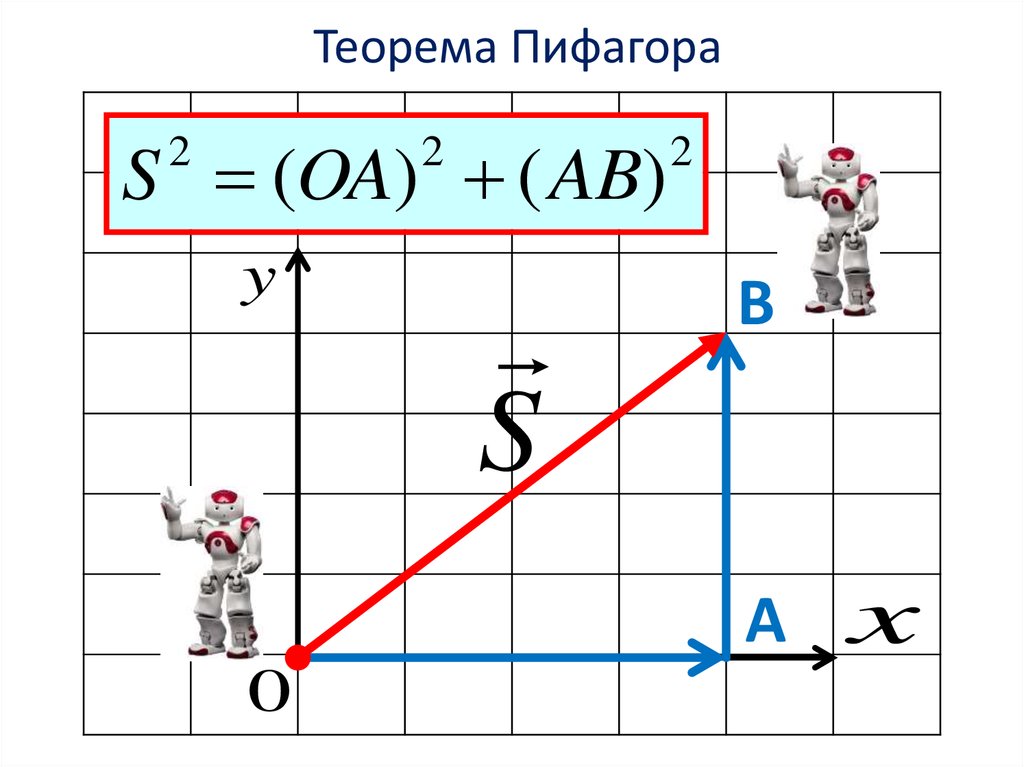
2. Теорема Пифагора
S (OA) ( AB)2
2
y
S
2
B
А x
0
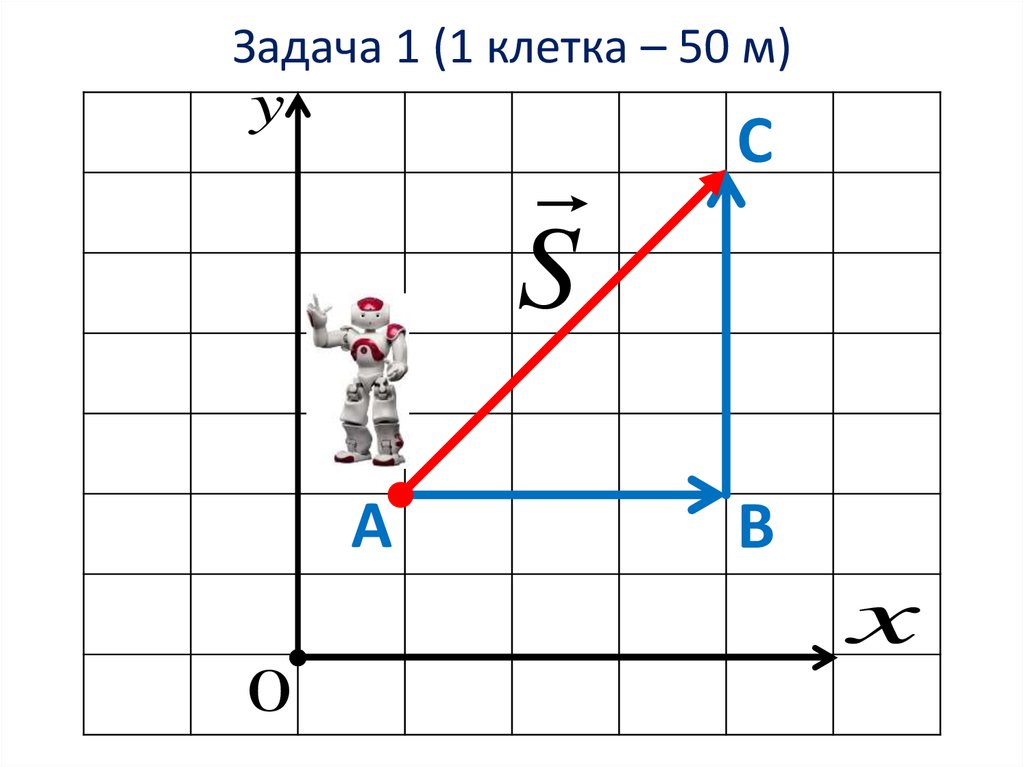
3. Задача 1 (1 клетка – 50 м)
yS
А
С
B
x
0
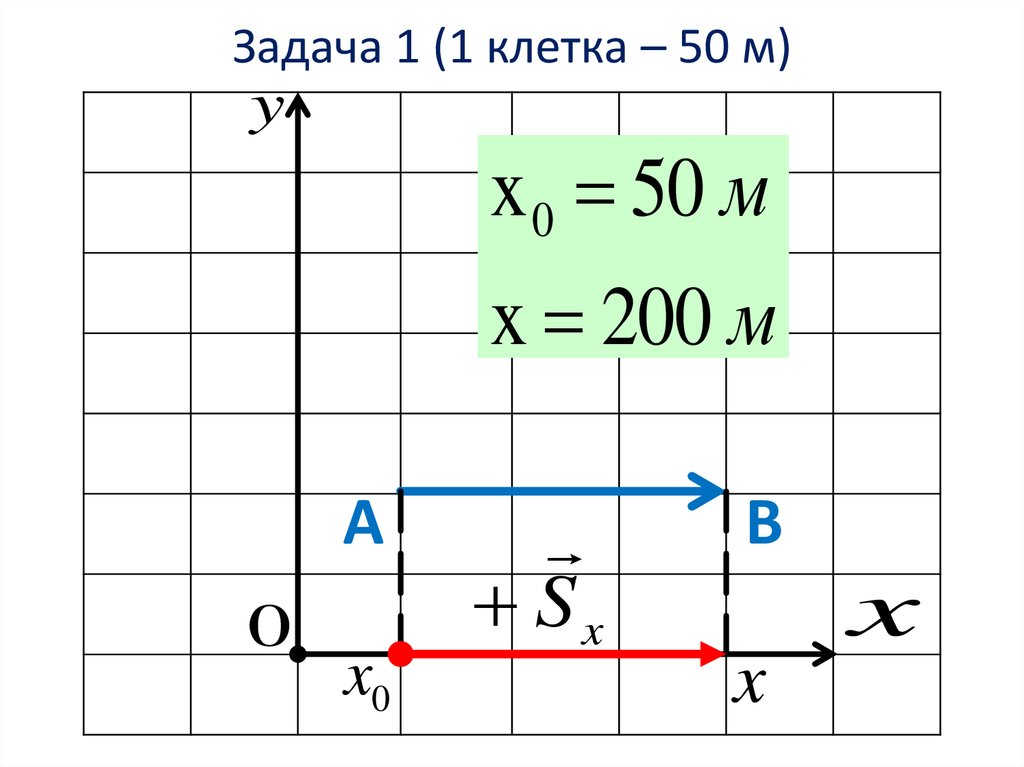
4. Задача 1 (1 клетка – 50 м)
yx 0 50 м
x 200 м
А
0
x0
Sx
B
x
x
5.
Проекция вектора – это отрезок,лежащий на выбранной оси
между перпендикулярами,
опущенными из начала и конца
вектора.
6. Проекция вектора на ось ОХ
x 0 начальная координатаx конечная координата
S x S x x x0 200 50 150 м
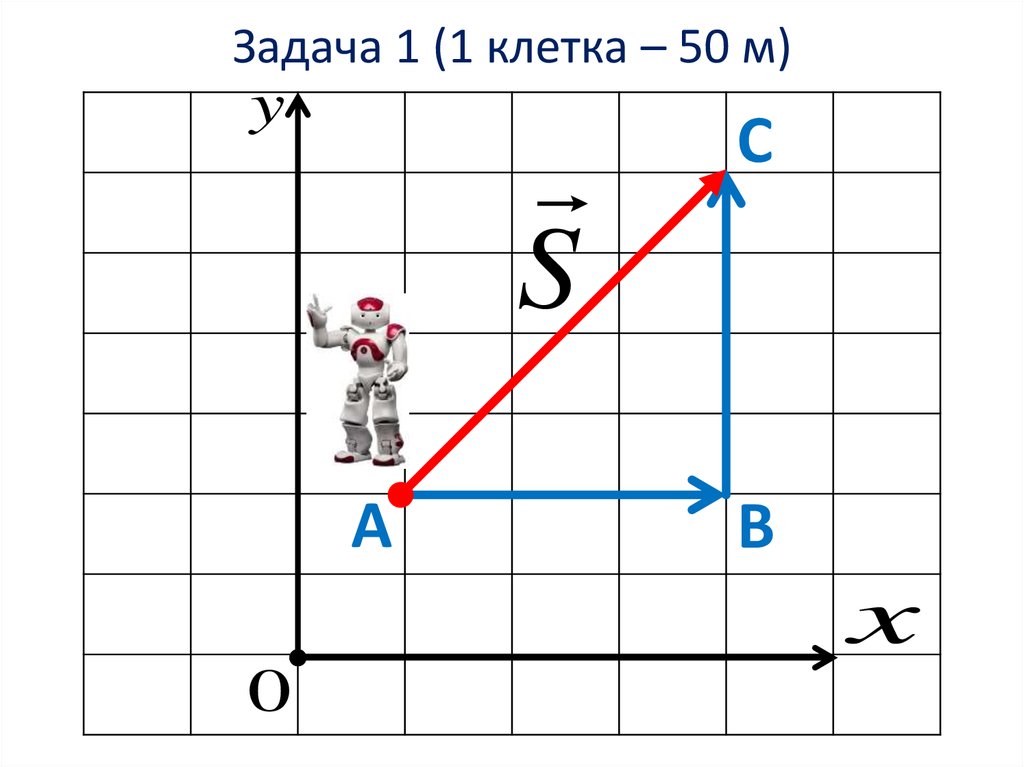
7. Задача 1 (1 клетка – 50 м)
yS
А
С
B
x
0
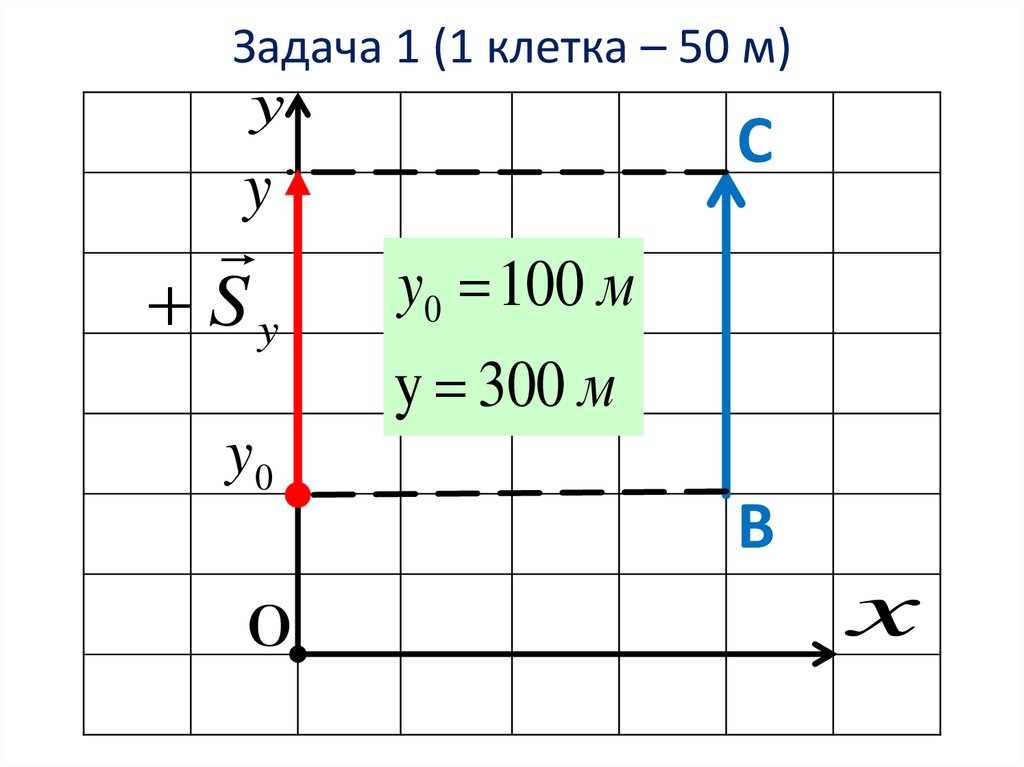
8. Задача 1 (1 клетка – 50 м)
yС
y
Sy
y0
0
y0 100 м
y 300 м
B
x
9.
Проекция вектора – это отрезок,лежащий на выбранной оси
между перпендикулярами,
опущенными из начала и конца
вектора.
10. Проекция вектора на ось ОY
y0 начальная координатаy конечная координата
S y S y y y0 300 100 200 м
11. Подведём итоги!
12. Вектор перемещения
l 350 м2
2
2
2
S S Sx S y
2
2
2
2
S S 200 150 62500
S S 62500 250 м
13. Вектор перемещения
координатный способ2
2
2
2
S S Sx S y
S x x x0
S y y y0
2
2
S S ( x x0 ) ( y y0 )
14. Решим задачу!
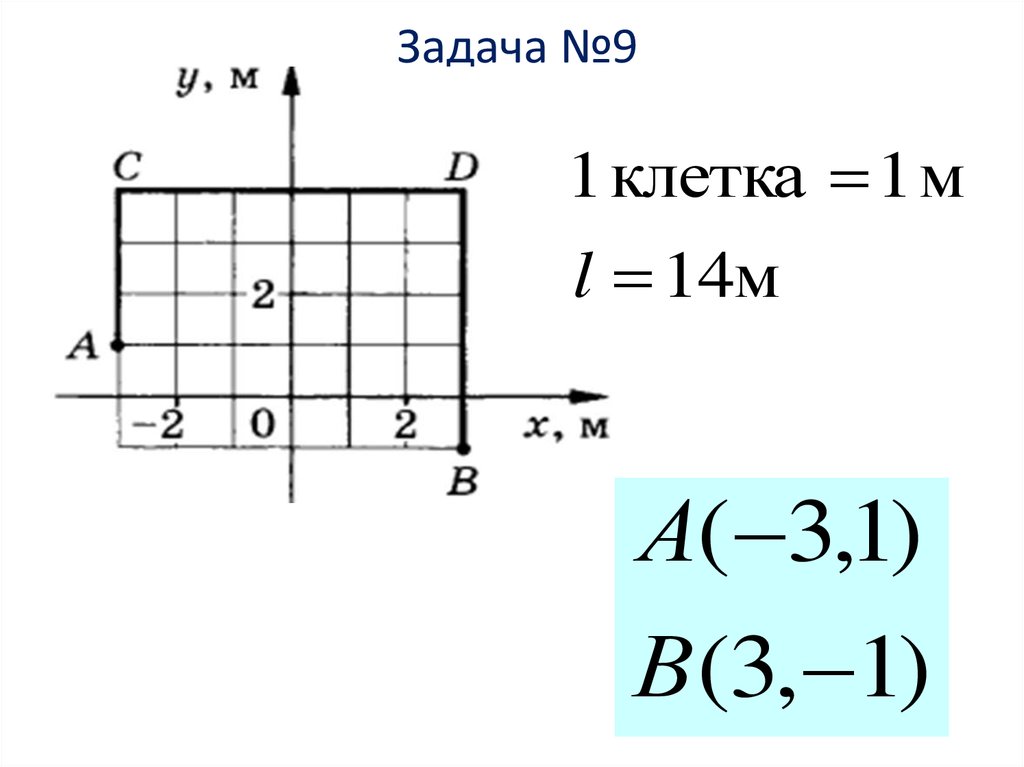
15. Задача №9
1 клетка 1 мl 14м
А( 3,1)
В (3, 1)
16. Задача №9
А( 3,1)В (3, 1)
S
x0 3, y0 1
x 3, y 1
2
2
S S ( x x0 ) ( y y0 )
2
2
2
2
S S (3 ( 3)) ( 1 1) 6 2 6,3
17.
Проекция вектора перемещенияy
y
Sy
y0
А
x0
S
Проекция вектора на ось
B
скалярная
векторная
Sx , S y
S x x x0
Sx
S y y y0
x
x
x0 , y 0 начальные координаты
x , y конечные координаты
Sx Sx
модуль вектора есть его длина
(скаляр)
S x S cos
S y S sin
S 2 S x2 S y2
КООРДИНАТНЫЙ СПОСОБ
S ( x x0 ) ( y y0 )
2
2











 Физика
Физика








