Похожие презентации:
Групповая скорость волн. Дисперсия волн. Колебания и волны. 15
1. Раздел курса «Колебания и волны»
ТемаГрупповая скорость волн.
Дисперсия волн.
2.
Бесконечная монохроматическая волна,уравнение которой имеет вид
( x, t ) A cos( t kx ),
не может быть использована для передачи
информации.
3.
Для того, чтобы волна могла переноситьинформацию, необходимо изменять со
временем (модулировать) её параметры А,
или . Соответственно существуют
амплитудная, частотная и фазовая
модуляции волны.
4. Рассмотрим волну с амплитудной модуляцией.
Для того, чтобы создавать волну,амплитуда которой изменяется со временем,
источник волны должен совершать
колебания то с большей, то с меньшей
амплитудой, то есть в простейшем случае
совершать биения.
5.
Ранее было показано, что биения возникаютпри сложении двух однонаправленных
гармонических колебаний, частоты которых 1
и 2 различны, но мало отличаются друг от
друга:
2 1 1, 2 .
Следовательно, источник, который совершает
биения, создает две гармонические волны,
бегущие в одном направлении, частоты которых
1 и 2.
6. Обе волны возбуждают одинаково направленные колебания в одних и тех же точках пространства. Получим уравнение результирующей
волнысчитая, что биения источника происходят при
сложении гармонических косинусоидальных
колебаний с нулевой начальной фазой и
одинаковыми амплитудами.
7.
1 2A cos 1t k1 x A cos 2t k2 x
k2 k1
2 1
2 A cos
t
x
2
2
k2 k1
2 1
cos
t
x .
2
2
8. «Фотография» полученной волны в некоторый момент времени имеет вид
Скорость перемещения в пространствемаксимума волнового пакета (точка *)
называется групповой скоростью Vгр волн,
составляющих волновой пакет.
9. Огибающая волнового пакета определяется в уравнении модулированной волны членом
k 2 k12 1
cos
t
2
2
x .
10.
В процессе перемещения такоймодулированной волны для точки, обозначенной
звездочкой (*), постоянной остается фаза,
стоящая в этом выражении:
2 1 k2 k1
t
x * const.
2
2
Здесь x* - координата максимума волнового
пакета.
11.
Поставим задачу: выразить групповуюскорость Vгр через циклические частоты 1,
2 и волновые числа k1, k2 волн,
составляющих волновой пакет.
12. Итак, показано, что групповая скорость волн равна производной от циклической частоты по волновому числу:
dVгр
.
dk
Поставим задачу: найти связь групповой и
фазовой скорости волны:
Vгр f Vф ?
13. Итак, показано, что групповая скорость волны выражается через фазовую скорость формулой
Vгр VфdVф
d
.
14. Рассмотрим три случая:
1) Vф f( ) – фазовая скорость не зависит отдлины волны (явление дисперсии волн
отсутствует);
dVф
0
d
15.
2) Vф растет с ростом длины волны , то естьdVф
d
0
(наблюдается нормальная дисперсия);
16.
3) Vф уменьшается с ростом длины волны,
то есть
dV
ф
d
0
(наблюдается аномальная дисперсия).
17.
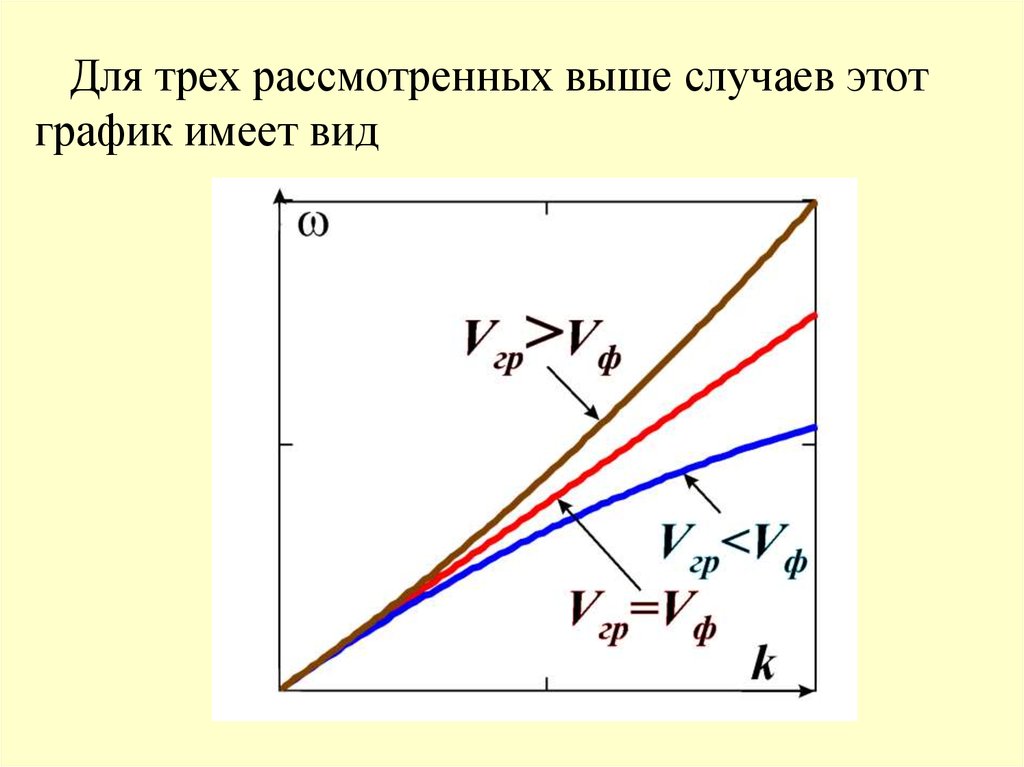
Итак,1) если дисперсия отсутствует, то групповая
скорость волн равна фазовой
Vгр Vф ;
2) если наблюдается нормальная дисперсия, то
групповая скорость волн меньше фазовой
Vгр Vф ;
3) если наблюдается аномальная дисперсия, то
групповая скорость волн больше фазовой
Vгр Vф .
18. Последовательные моментальные «фотографии» волнового пакета в моменты времени t1, t2, t3 а) нормальная дисперсия, б) аномальная
дисперсия.19. График зависимости циклической частоты волны от волнового числа =f(k) называется дисперсионным.
График зависимости циклической частотыволны от волнового числа =f(k) называется
дисперсионным.
20.
Для трех рассмотренных выше случаев этотграфик имеет вид






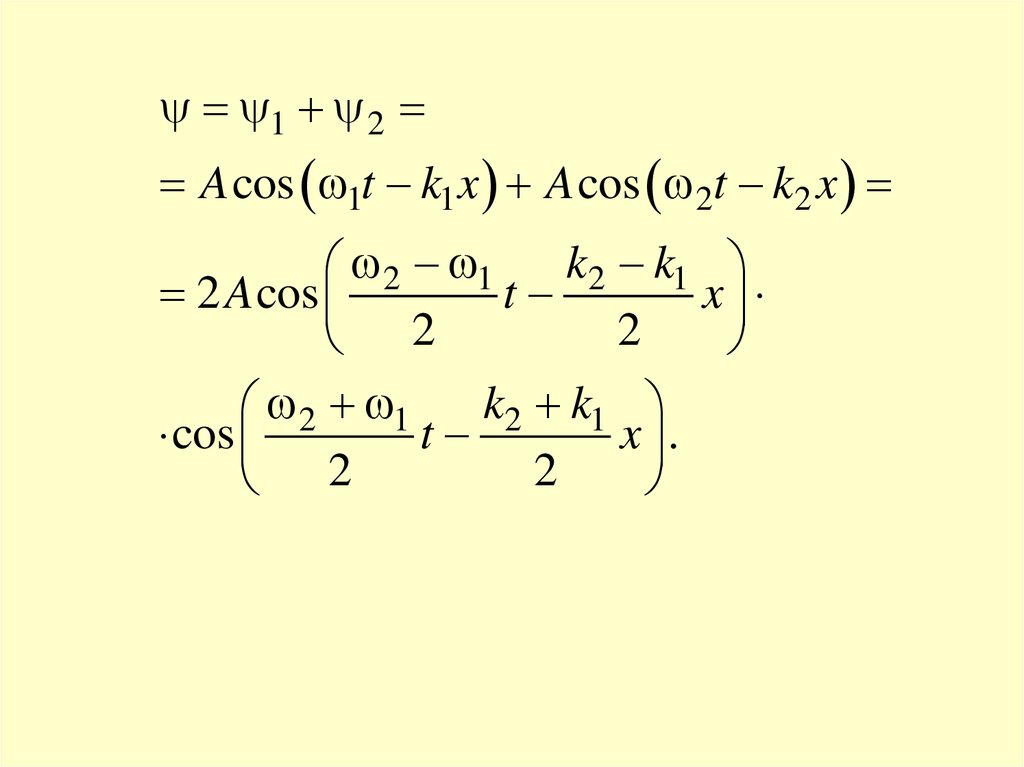












 Физика
Физика








