Похожие презентации:
Преобразование тригонометрических выражений. Вывод тригонометрических формул
1.
Университетский лицей №1523Предуниверситария НИЯУ МИФИ
Лекции по алгебре и началам анализа
10 класс
© Хомутова
Лариса Юрьевна
2.
Преобразованиетригонометрических
выражений
(вывод тригонометрических
формул)
3.
I-a. Формулы приведенияВыведем вспомогательные формулы, позволяющие
находить
sin
cos и
2
2
по тригонометрическим функциям угла .
4.
(0; / 2 )AOB = A1OC по гипотенузе и
острому углу: AO = 1 = A1O.
A1OC = / 2 - COA = AOB;
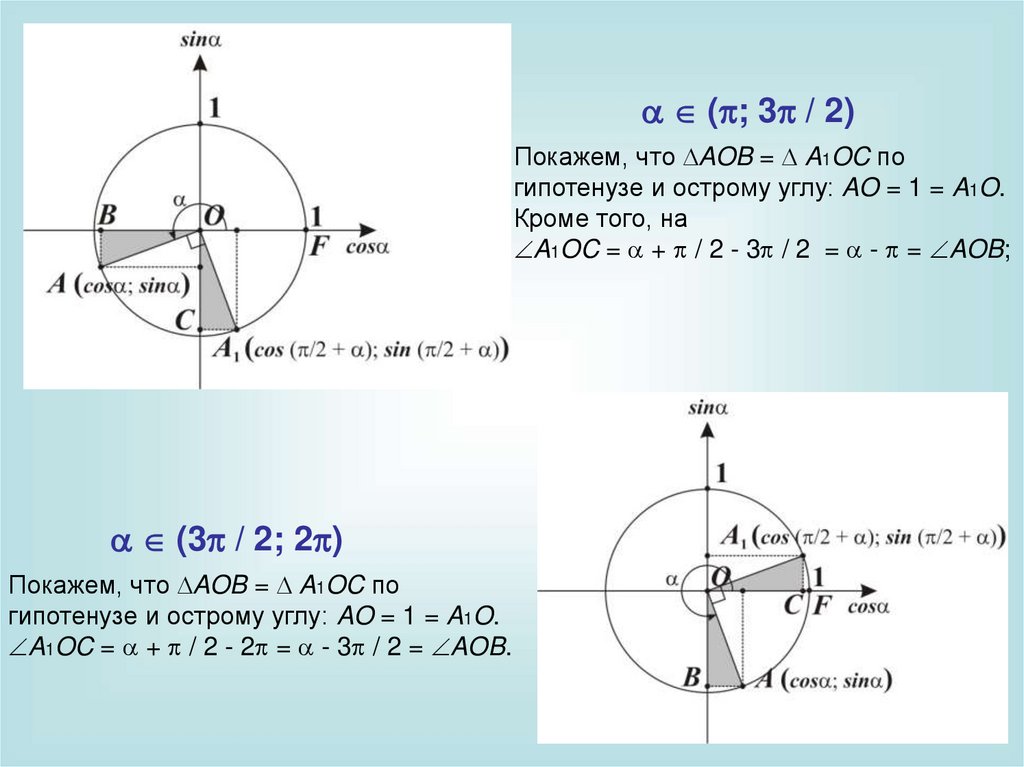
( / 2; )
AOB = A1OC по гипотенузе и острому
углу: AO = 1 = A1O.
A1OC = + / 2 - = - / 2 = AOB;
5.
( ; 3 / 2)Покажем, что AOB = A1OC по
гипотенузе и острому углу: AO = 1 = A1O.
Кроме того, на
A1OC = + / 2 - 3 / 2 = - = AOB;
(3 / 2; 2 )
Покажем, что AOB = A1OC по
гипотенузе и острому углу: AO = 1 = A1O.
A1OC = + / 2 - 2 = - 3 / 2 = AOB.
6.
I-a. Формулы приведения,
.
cos sin
2
sin cos
2
7.
I-b. Формулы приведенияВыведенные формулы сложения позволяют получить
формулы приведения, упрощающие тригонометрические
функции углов вида k 2
cos 3 2 cos3 2 cos sin 3 2 sin sin
1
0
:
/2– /2+
–
+
3 / 2 –
3 / 2 +
2 –
2 +
sin
cos
cos
sin
–sin
–cos
–cos
–sin
sin
cos
sin
–sin
–cos
–cos
–sin
sin
cos
cos
tg
ctg
–ctg
–tg
tg
ctg
–ctg
–tg
tg
ctg
tg
–tg
–ctg
ctg
tg
–tg
–ctg
ctg
8.
II. Формулы сложенияM ( )
j
M ( )
M ( )
2) Введем единичные вектора
i и j
0
1) Отметим на единичной
окружности точки M ( ) и
3) M ( ) cos ; sin
i
M ( ) cos ; sin
4) OM ( ) (cos ; sin )
OM ( ) (cos ; sin )
5) Угол между векторами OM ( ) и OM ( ) равен
9.
6) По свойству скалярного произведения найдемOM ( ) OM 1 1 cos cos cos cos sin sin
7) Учитывая четность тригонометрических функций получаем
cos cos cos cos( ) sin sin
cos cos sin sin
10.
8)sin cos cos ( )
2
2
cos cos sin sin
2
2
sin cos cos sin
9)
sin cos cos ( )
2
2
cos cos sin sin
2
2
sin cos cos sin
11.
II. Формулы сложенияsin sin cos cos sin ,
cos cos cos sin sin
12.
sinsin cos cos sin
tg
cos cos cos sin sin
Поделим числитель и знаменатель полученной дроби на
cos cos
cos 0 и cos 0 , т.е. в случае, когда
tg
и
tg определены:
tg tg
tg
1 tg tg
cos
cos cos sin sin ctg ctg 1
ctg
sin sin cos cos sin
ctg ctg
13.
II. Формулы сложенияtg tg
tg
,
1 tg tg
ctg ctg 1
ctg
ctg ctg
14.
III. Формулы двойных угловЧтобы вывести формулы для вычисления
тригонометрических функций двойного аргумента,
подставим = в формулы сложения:
sin sin cos cos sin ,
sin 2 sin cos cos sin 2sin cos ,
cos cos cos sin sin ,
tg tg
,
1 tg tg
ctg ctg 1
ctg
ctg ctg
tg
cos 2 cos cos sin sin cos 2 sin 2 ,
tg tg
2tg
tg 2
,
2
1 tg tg 1 tg
ctg ctg 1 ctg 2 1
ctg 2
.
ctg ctg
2ctg
15.
III. Формулы двойных угловsin 2 2sin cos
cos 2 cos sin
2
2
cos 2 cos 2 sin 2 1 sin 2 sin 2 1 2sin 2
cos 2 cos sin cos 1 cos 2 cos 1
2
2
2
2
2
16.
III. Формулы двойных углов2tg
tg 2
2
1 tg
ctg 1
ctg 2
2ctg
2
17.
\ : cos22sin cos
sin 2 2sin cos
sin 2 cos2
2tg
cos 0 tg 2 1
\ : sin 2
2sin cos
sin 2 2sin cos
sin 2 cos2
\ : cos2
cos sin
2
2
cos 2 cos sin
sin 2 cos2
2
2
2
1 tg 2
cos 0 tg 2 1
\ : sin 2
cos sin
2
2
cos 2 cos sin
2
2
sin cos
2
2ctg
sin 0 ctg 2 1
ctg 2 1
sin 0 1 ctg 2
18.
III. Формулы двойных углов2tg
sin 2 2
tg 1
2ctg
sin 2
ctg 2 1
1 tg
cos 2
1 tg 2
2
ctg 2 1
cos 2
ctg 2 1
19.
IV. Формулы тройных угловsin 3 sin 2 sin 2 cos cos 2 sin 2sin cos 2 1 2sin 2 sin
2sin 1 sin 2 sin 2sin 3 2sin 2sin 3 sin 2sin 3 3sin 4sin 3
cos 3 cos 2 cos 2 cos sin 2 sin 2 cos 2 1 cos 2sin 2 cos
.
2 cos3 cos 2 1 cos 2 cos 2 cos 3 cos 2 cos 2 cos 3 4 cos 3 3cos
20.
tg 33sin sin 2 cos 2 4sin 3
sin 3 3sin 4sin
3
3
2
2
cos 3 4 cos 3cos 4 cos 3cos sin cos
3
\ : cos3
3sin cos sin
cos3 3cos sin 2
2
.
3
3tg tg 3
cos 0 1 3tg 2
\ : sin 3
cos 3cos sin
ctg 3
3sin cos 2 sin 3
3
2
ctg 3 3ctg 3ctg ctg 3
2
3ctg 1
1 3ctg 2
sin 0
21.
IV. Формулы тройных угловsin3 3sin 4sin
3
cos3 4cos3 3cos
3tg tg 3
tg 3
1 3tg 2
3ctg ctg 3
ctg 3
1 3ctg 2
22.
V. Формулы половинных угловcos 1 2sin
2
1 cos
sin
2
2
cos 2cos
1
2
1 cos
cos
2
2
2
.
2
2
2
23.
\ 2 cossin 2
tg
2
cos 2
2
2sin 2 cos 2
sin
2
1 cos
2 cos 2
2
sin
2 1 cos
2
tg
2
2 cos 2 1 cos
;
\ 2sin
cos 2
ctg
2
sin 2
2
2sin 2 cos 2
sin
2
1 cos
2sin 2
2
cos
2 1 cos
2
ctg
2
2 sin 2 1 cos
24.
V. Формулы половинных углов1 cos
sin
2
2
2
1 cos
cos
2
2
1 cos
sin
2
tg
tg
2 1 cos
2 1 cos
2
,
,
.
.
sin
ctg
2 1 cos
1 cos
ctg
2 1 cos
2
25.
VI. Формулы преобразования произведениятригонометрических функций в сумму
sin sin cos cos sin ,
sin sin cos cos sin ,
cos cos cos sin sin ,
cos cos cos sin sin .
.
1
2
3
4
Сложив почленно равенства (1) и (2), получим:
.
sin cos
1
sin sin
2
Сложив почленно равенства (3) и (4), получим:
1
cos cos cos cos
2
Вычтя из равенства (4) равенство (3), получим:
sin sin
1
cos cos
2
26.
VI. Формулы преобразования произведениятригонометрических функций в сумму
1
sin cos sin sin
2
1
cos cos cos cos
2
1
sin sin cos cos
2
27.
VII. Формулы преобразования суммытригонометрических функций в
произведение
sin sin sin
cos
cos
sin
sin
cos
sin
sin
2
2
2
2
2
2
2
2
2
2
cos
sin
2sin
cos
2
2
2
2
sin sin sin
sin
sin
cos
cos
sin
sin
cos
2
2
2
2
2
2
2
2
2
2
.
cos
sin
2cos
sin
2
2
2
2
28.
cos cos coscos
sin
sin
cos
cos
cos
cos
2
2
2
2
2
2
2
2
2
2
sin
sin
2cos
cos
2
2
2
2
.
cos cos cos
cos
sin
sin
cos
cos
cos
cos
2
2
2
2
2
2
2
2
2
2
sin
.
sin
2sin
sin
2sin
sin
2
2
2
2
2
2
29.
VII. Формулы преобразования суммытригонометрических функций в
произведение
sin sin 2sin 2 cos 2 ,
sin sin 2 cos sin ,
2
2
cos cos 2 cos cos ,
2
2
cos cos 2sin
sin
.
2
2








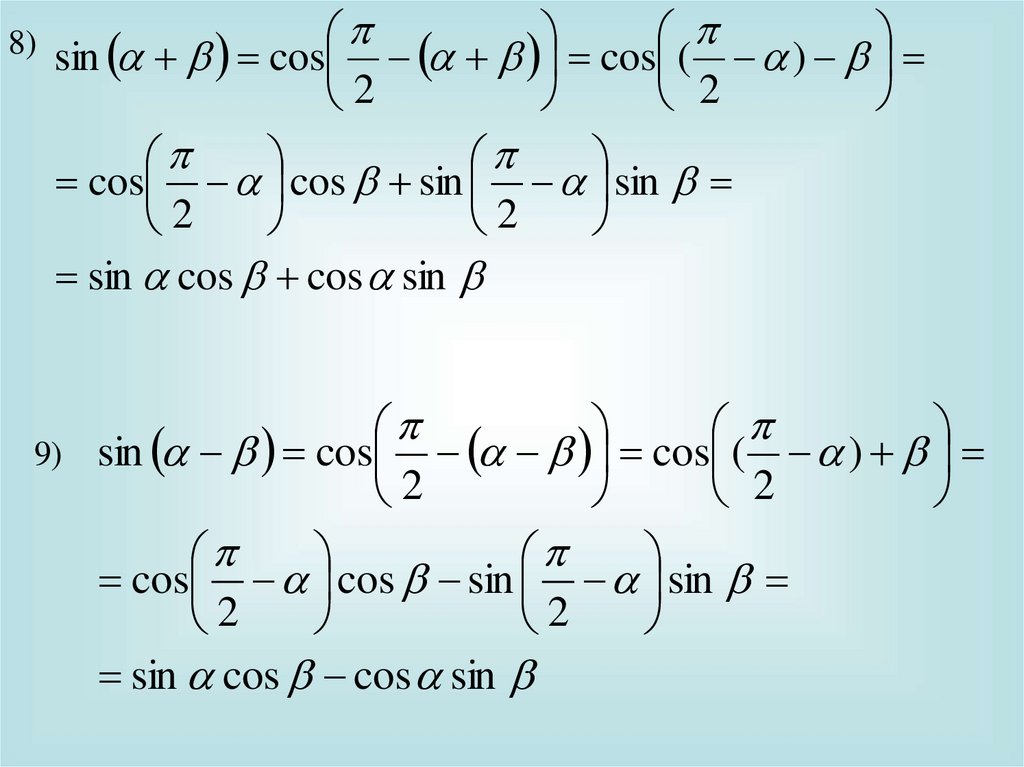









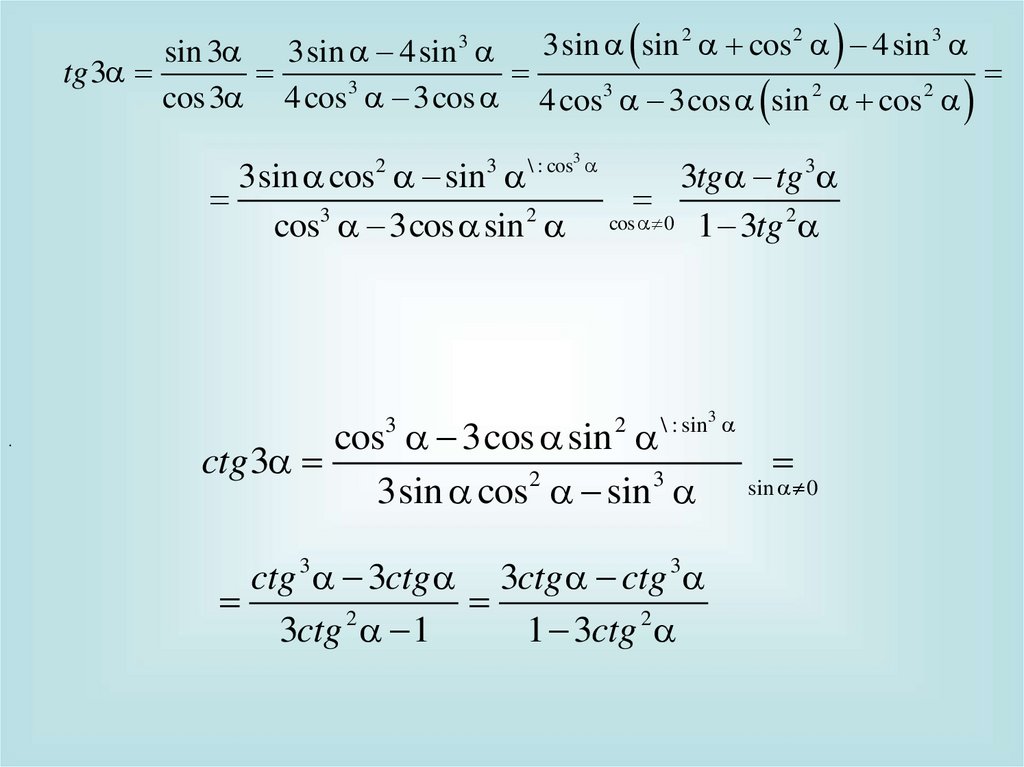









 Математика
Математика








