Гидрогазодинамика. Особенности струйного течения. (Лекция 5)

1. Тема 1. Гидрогазодинамика

Лекция 5

2.

§ 11. Особенности струйного течения
Свободной турбулентной называется струя,
распространяющаяся вдали от твердых поверхностей.
Это один из видов свободного пограничного слоя.
Из-за отсутствия стабилизирующего влияния
стенки струйные потоки почти всегда турбулентны,
кроме того, в них отсутствует ламинарный подслой.
Затопленной называется свободная турбулентная струя,
истекающая в пространство, заполненное средой
с теми же физическими свойствами, что и
жидкость, образующая струю. Свободные
турбулентные струи могут быть осесимметричными –
истекающими
из сопла круглого
сечения и плоскими – истекающими из щелевого
сопла.
2

3.

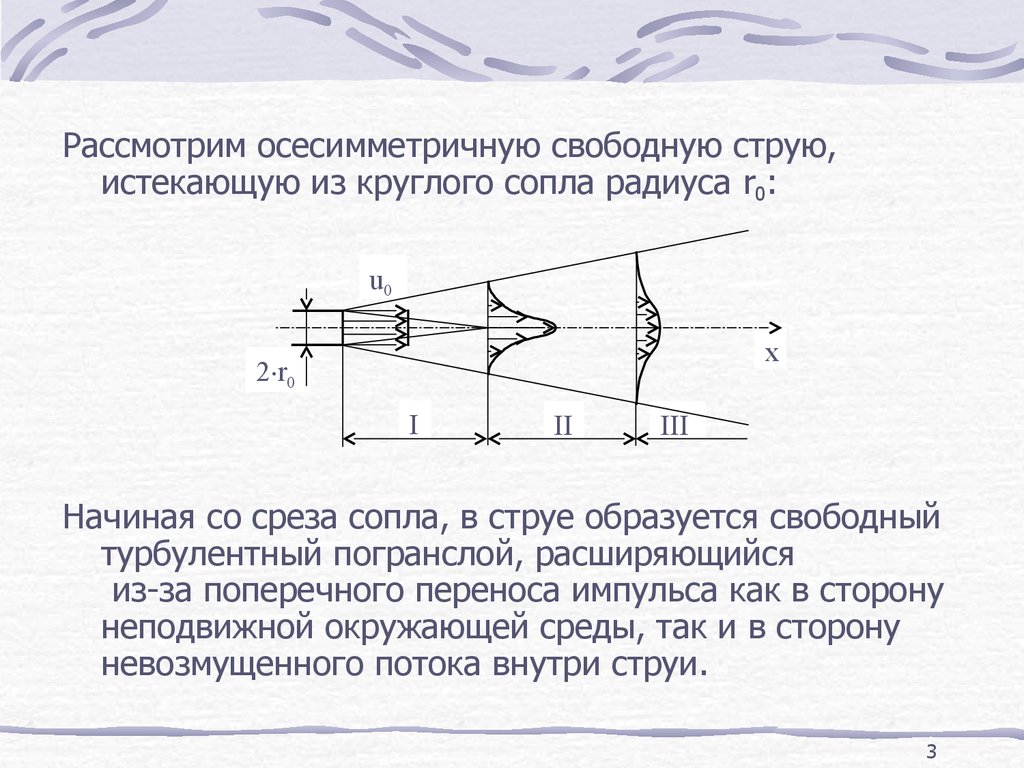
Рассмотрим осесимметричную свободную струю,
истекающую из круглого сопла радиуса r0:
u0
x
2 r0
I
II
III
Начиная со среза сопла, в струе образуется свободный
турбулентный погранслой, расширяющийся
из-за поперечного переноса импульса как в сторону
неподвижной окружающей среды, так и в сторону
невозмущенного потока внутри струи.
3

4.

Начальным называется участок, на протяжении которого
продолжает существовать невозмущенный поток
внутри струи (I). На переходном участке происходит
перестройка поперечного профиля скорости в струе
(II), на основном участке (III) поперечные профили
скорости являются автомодельными, то есть, будучи
построенными в безразмерных координатах
u
y
um
R ,
где um – скорость на оси, а R – радиус струи в данном
сечении, эти профили ложатся на одну и ту же кривую.
Струи, истекающие из сопел конечного размера,
становятся автомодельными, начиная с некоторого
расстояния от сопла, где его конечный размер
перестает влиять на развитие течения.
4

5.

Экспериментально установленным фактом является
прямолинейность границ свободных турбулентных
струй:
R = r0 + c x ,
где с – тангенс полуугла раскрытия струи.
В свободных турбулентных струях отсутствуют силы
давления. Кроме того, на границах струи отсутствуют
и силы трения, так как там обращается в ноль
не только скорость, но и ее производная по
поперечной координате. Следовательно, поток
импульса по длине струи не изменяется, так как на
контрольный объем, ограниченный двумя поперечными
сечениями
и боковой поверхностью
струи, никакие внешние силы не действуют. В
соответствии с законом сохранения импульса,
проходящие через эти сечения потоки импульса равны.
5

6.

Воспользовавшись этими свойствами, найдем закон
изменения скорости на оси основного участка струи
um (x). Поток импульса через поперечное сечение
I ρ u 2 df
струи
F
.
Для круглой струи f = y2, откуда df = 2 y dy,
и с учетом постоянства плотности
получаем:
R
I 2 π ρ u 2 ydy
0
.
Для представления подынтегрального выражения 2
um
в безразмерном виде вынесем2 за знак интеграла
не зависящие от1текущего
радиуса
y
u
y
y
2
2
π 2ρ: u R
величины I 2и R
d
m
u
0
m
R R
.
6

7.

Вводя обозначение η=y/R и учитывая автомодельность
поперечных профилей скорости, получим:
1
I 2 π ρ u 2m R 2 2 η ηdη .
0
Интеграл в правой части этого выражения –
постоянное число, так как ( ) не зависит от x,
а пределы интегрирования тоже являются
числами. Обозначим эту величину K1, тогда
I 2 π K1 ρ u 2m R 2 .
7

8.

Приравняв последнее выражение к начальному потоку
импульса
I 0 ρ u 02 π r02 ,
получим после сокращений и с учетом линейного
нарастания радиуса по длине:
u 0 r0
um
,
2 K1 r0 c x
где K1 – коэффициент, находимый из аппроксимации
безразмерного профиля скорости какой-либо
подходящей функцией.
8

9.

Объемный расход через поперечное сечение струи
R
1
u y y
2
V udf 2 π u ydy 2 π u m R
d
u R R
F
0
0
m
1
2 π u m R 2 η ηdη .
0
Интеграл в правой части тоже является числом,
которое обозначим K2. Подставляя вместо um
его значение, а вместо радиуса струи – закон
его изменения по длине, после сокращений
получим
2 K
V
2
K1
π r0 u 0 (r0 c x)
.
9

10.

Рассчитаем изменение потока кинетической энергии
по длине струи, то есть величину энергии,
проходящей через все поперечное сечение струи за
единицу времени. Плотность потока кинетической
энергии – половина произведения плотности потока
массы u на квадрат скорости, то есть эта величина
3
равна u
/2. Тогда:
3
3
R
1
ρ u
y y
3
3
2 u
EK
df π ρ u ydy π ρ u m R
d
F 2
0
0 u m R R
π ρ u 3m R 2
1
3
η ηdη
0
.
Обозначив интеграл в правой части K3, используя законы
изменения um и R по длине струи, получим:
r0 u 0 3 r0 c x 2
π ρ K 3 r03 u 30
E K π ρ
K3
3
3/ 2
.
2
2
K
2 K1 r0 c x
1 r0 c x
10

11.

Изобразим изменение основных характеристик
осесимметричной турбулентной струи по ее длине:
I, p, V,
um, EK
I
p
V
um
EK
x
В плоской струе расход нарастает x , а осевая
скорость и поток кинетической энергии уменьшается
x
1/
. Более медленное затухание
плоской струи объясняется меньшей поверхностью
соприкосновения с окружающей средой и меньшей
интенсивностью вовлечения окружающей среды в
движение.
11