Looping pendulum

1. Looping pendulum

Problem №14
Looping pendulum
Connect two loads, one heavy and one light,
with a string over a horizontal rod and lift
up the heavy load by pulling down the light
one. Release the light load and it will sweep
around the rod, keeping the heavy load from
falling to the ground. Investigate this
phenomenon.
Team Russia
Reporter: Ivan Polonik

2.

Plan
Qualitative explanation: Energy transfer
Parametric investigation
Boundary conditions: Mass, initial angle and length
relationship
Different mode: step falling
2

3.

Setup scheme
•Human factor can be neglected •LED increases
•Fixed
rod line
Fishing
theoscillations
accuracy of
•No
construction
•High accuracy of controlling initial
parameters
measurements
•Inextensible
•Weightlessof load location
•Mass of heavy
load can be
increased piece
by piece
pin
nut
3

4.

μ
v
||
v
||
˫
˫
v W v K U
L
Light weight energy, mJ
Qualitative explanation
Data from
video analyses
Heavy load stops
No energy transfer
Energy transfer
u W K U
u H
Light load raises because of
energy transfer
Heavy load is accelerated by gravity force
and is decelerated by friction force
Qualitative explanation
Quantitative model
Parametric investigation
4

5.

Components of the system
Things to describe
Rod + string – friction force
String – kinematic ratio
Light load – dynamics
Heavy load - dynamics
Qualitative explanation
Quantitative model
Parametric investigation
5

6.

Mathematical model
Theory assumptions:
Drag force is
neglectable
Heavy load
falls vertically
String:
weightless
inextensible
Qualitative explanation
String lays
turn to turn
Quantitative model
Parametric investigation
6

7.

3 - dimensional movement
T cos
12
T
T sin
Z
Qualitative explanation
In all other exp eriments
5 cos(5 ) 0.996 1
Mainly problem can be
solved as
2-dimensional
Quantitative model
Parametric investigation
7

8.

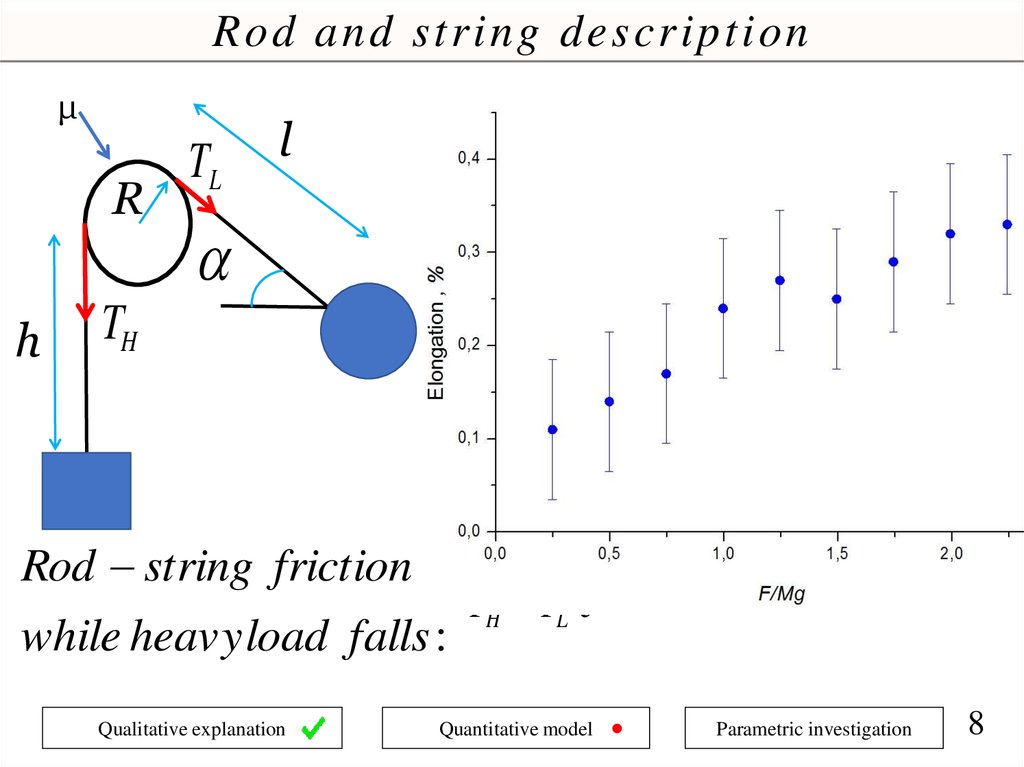
Rod and string description
μ
R
h
TL
l
Inextensible string :
l R h const
.. .. ..
TH
l R h 0
Rod string friction
while heavy load falls :
Qualitative explanation
TH TL e
Quantitative model
2
Euler' s formula
Parametric investigation
8

9.

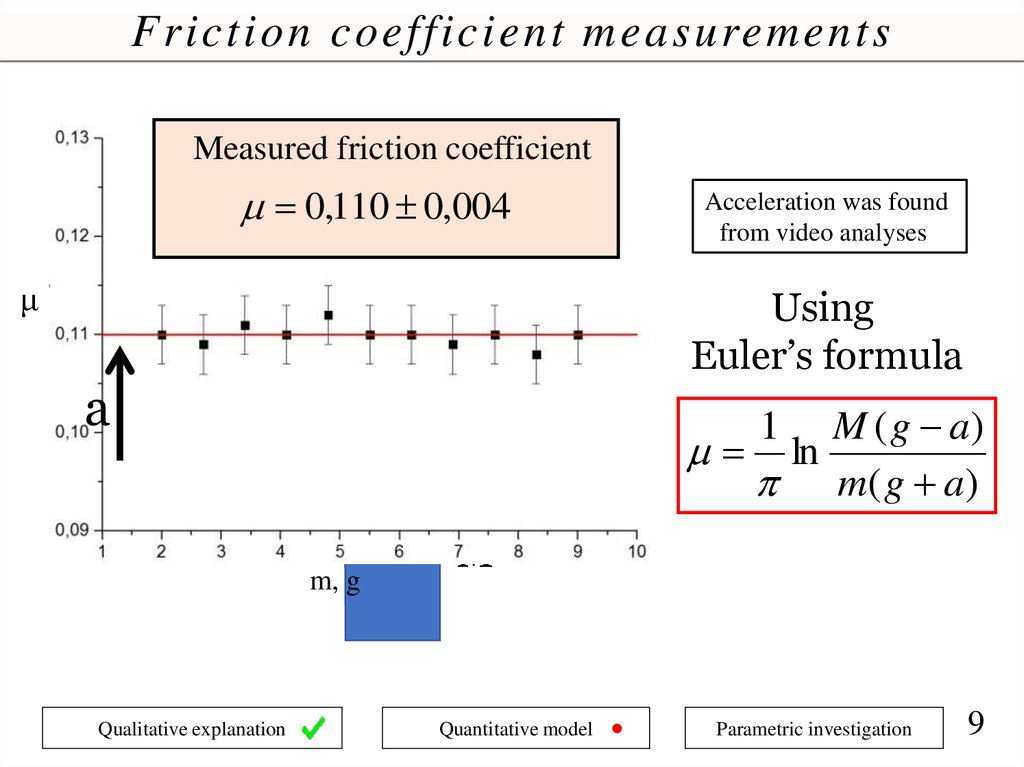
Friction coefficient measurements
Measured friction coefficient
0,110 0,004
π
μ
M ( g a)
ln
m( g a)
1
m
m, g
Qualitative explanation
Using
Euler’s formula
a
a
Acceleration was found
from video analyses
M
Quantitative model
Parametric investigation
9

10.

Heavy load movement
Fdrag
TH
Fdrag
Fdrag
1
C x v 2 S C x 0.85
2
7 10 5 N Mg 3 10 1 N
Heavy load falls vertically
Mg
4 000
max
Fdrag
h
S
Drag force can be neglected
II Newton law
v
Mg
Qualitative explanation
..
on vertical axis : M h Mg TH
Quantitative model
Parametric investigation
10

11.

Tension force acting on the light load
α
h
˫
v
..
.. ....
TL
l
TL
vr
TL
2
TL m( g sin ) h RR
) l )
.
v l
˫
α
mg
mg
mg
˫
R
l
Gravity
component
Inextensibility
component
Centrifugal
component
TLmax
90
max
Fdrag
1
Fdrag C x v 2 S C x 0.47 S 4 r 2
2
Drag force can be neglected
h
Qualitative explanation
Found value of Tension
force
Quantitative model
Parametric investigation
11

12.

Rotation of light load
О
Torque equation
about point O :
l
R
α
TL
mg
..
r
2 2
I mr
5
Tension
force torque
Inconstant moment
of inertia
..
dL
( I m(l 2 R 2 )) 2ml l mg l R cos TL R
dt
Described light load movement
Qualitative explanation
Quantitative model
Parametric investigation
12

13.

Numerical solution
μ
.
l
R
..
TL
α
h
mg
..
m( l R g cos 2l l ) TL R
m(l 2 R 2 ) I
..
TH
..
TL m(( ) l h R g sin )
2
TL (t 0) 0
Mg
..
TL e
h g
( )
2
M
Set of equations was solved numerically (iteratively)
Qualitative explanation
Quantitative model
Parametric investigation
13

14.

Comparing the dynamics of the system
Qualitative explanation
Quantitative model
Parametric investigation
14

15.

Legend
l0
ϕc
m
r
0
2
m
M
H
m – mass of light load
M – mass of heavy load
l – distance between light
Load and the rod
µ – friction coefficient
H- height heavy load goes down
t- time of going down
φ- angle of contact
between string and rod
φcrit- φ at the moment of heavy
load stopping
M

16.

ϕ, rad
H, mm
Heavy load mass influence
M, g
M, g
The higher heavy load mass
the higher critical angle.
Qualitative explanation
The higher heavy load mass
the higher H.
Quantitative model
Parametric investigation
16

17.

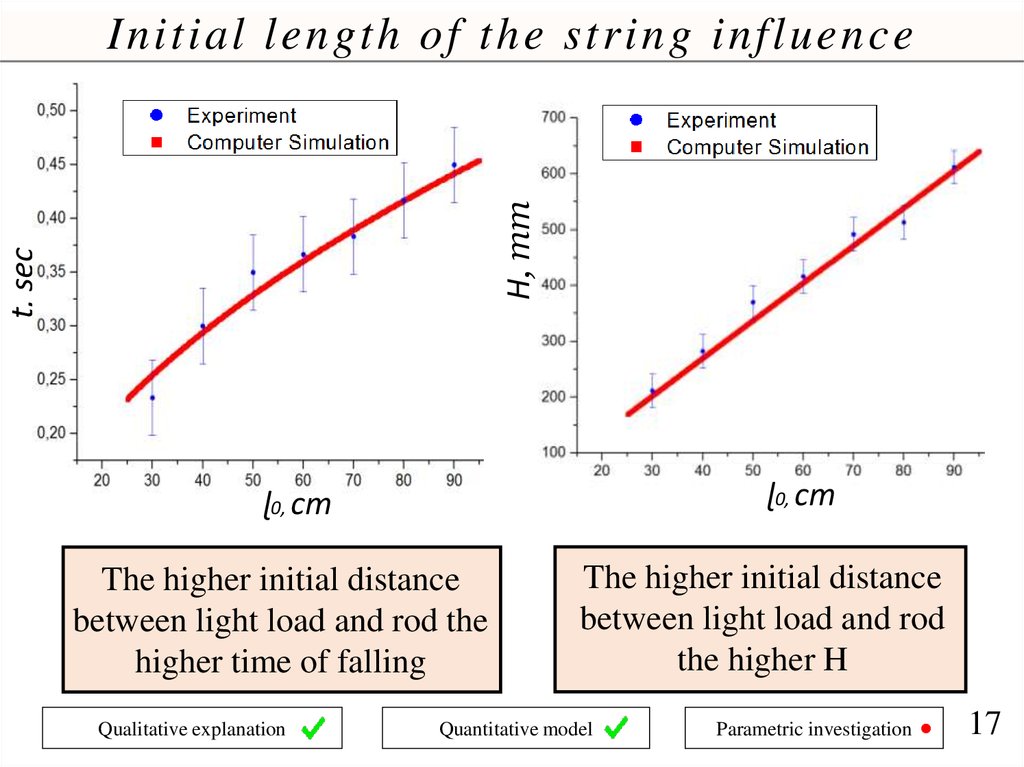
t, sec
H, mm
Initial length of the string influence
ɭ0, cm
ɭ0, cm
The higher initial distance
between light load and rod the
higher time of falling
Qualitative explanation
The higher initial distance
between light load and rod
the higher H
Quantitative model
Parametric investigation
17

18.

Whole parametric investigation
l0, cm
α0, rad
m, g
M
,g
ϕ,
rad
H,
mm
t,
sec
Qualitative explanation
Quantitative model
Parametric investigation
18

19.

Influence of the friction coefficient
Scotch tape
μ=0.18
String
μ=0.27
Duct tape
μ=0.32
Rod
μ=0.11
Qualitative explanation
Quantitative model
Parametric investigation
19

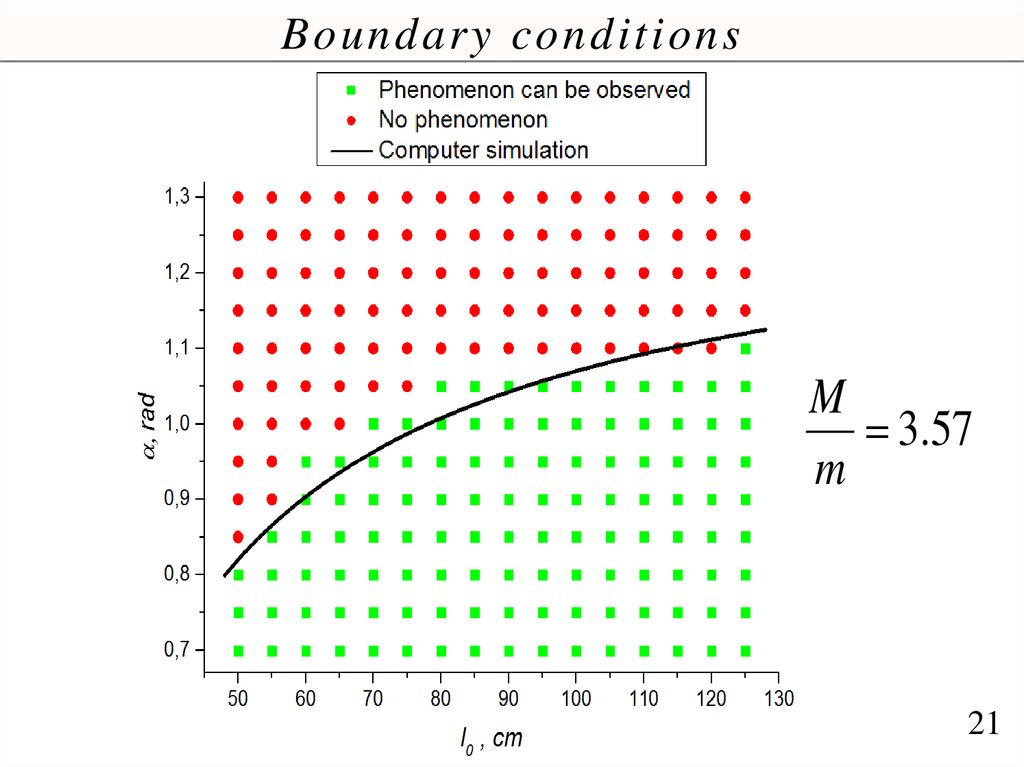
20.

Boundary conditions
3
TH Mg
TL mg
M/m=2.75
TH
Mg mg
M/m=2.95
TL
M 3
e
m
M
Theory prediction
2.82
m
M
2.82 no phenomenon
m
20

21.

Boundary conditions
M
3.57
m
21

22.

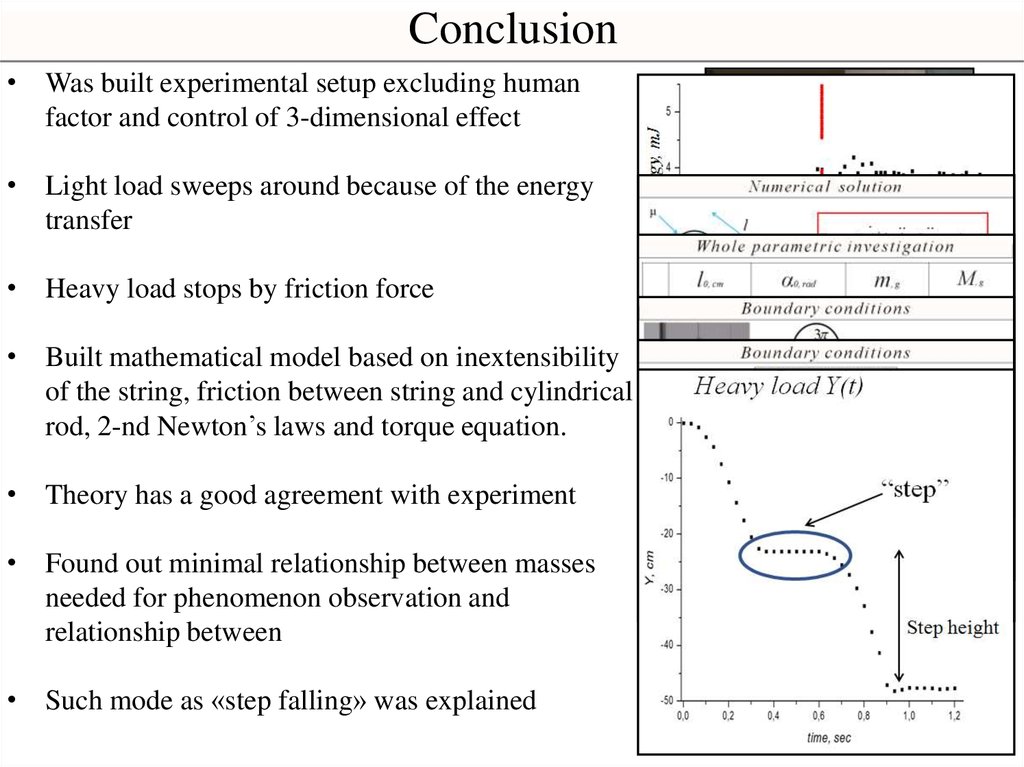
«Step» falling of heavy load
Heavy load Y(t)
“step”
Step height
Qualitative explanation
Quantitative model
Parametric investigation
22

23.

«Step» falling
v
Step height, mm
ТL’’
u
ТL’
M
3
5
m
Т1=Mg
Т1=Mg
ТL
v
Step falling can be observed
with small mass relationship
23

24.

Conclusion
• Was built experimental setup excluding human
factor and control of 3-dimensional effect
• Light load sweeps around because of the energy
transfer
• Heavy load stops by friction force
• Built mathematical model based on inextensibility
of the string, friction between string and cylindrical
rod, 2-nd Newton’s laws and torque equation.
• Theory has a good agreement with experiment
• Found out minimal relationship between masses
needed for phenomenon observation and
relationship between
• Such mode as «step falling» was explained
24

25. Thank you for your attention!

Connect two loads, one heavy and one light, with a string over a
horizontal rod and lift up the heavy load by pulling down the light
one. Release the light load and it will sweep around the rod, keeping
the heavy load from falling to the ground. Investigate this
phenomenon.
Also was investigated:
• Massive string
•Back sweeping
• Rod strike of light load
• Swinging of heavy load

26.

Additional slides

27.

View from above
Back sweeping
M
1.6 2.82
m
In this case 3dimensional of the
problem can’t be
neglected
27

28.

28

29. Key observation

Quantitative model
Quality explanation
Parametric investigation
Key observation
y, cm
Trajectory of light load
Parameters
m=1g
M = 10 g
l = 65 cm
ϕ0 = 90°
20
0
x, cm
50
25
y, cm
0
Law of motion of heavy load
T<Mg
0
Trajectory of light load is
a spiral. After heavy load
stop spiral pitch becomes
constant
T>Mg
-10
0,1
0,2
0,3
t, se
29

30. Dynamics of light load

Quantitative model
Quality explanation
Parametric investigation
Dynamics of light load
l
h
R
αR
TA
2
FCor
T2 m( l h h
R R g sin )
2
acentr
О
mg
Centrifugal InextensibilityGravity
component component component
Finer
T2
v
||
FCor
v =wl
˫
О
.. .. .. ..
v mg Finer
˫
A
30

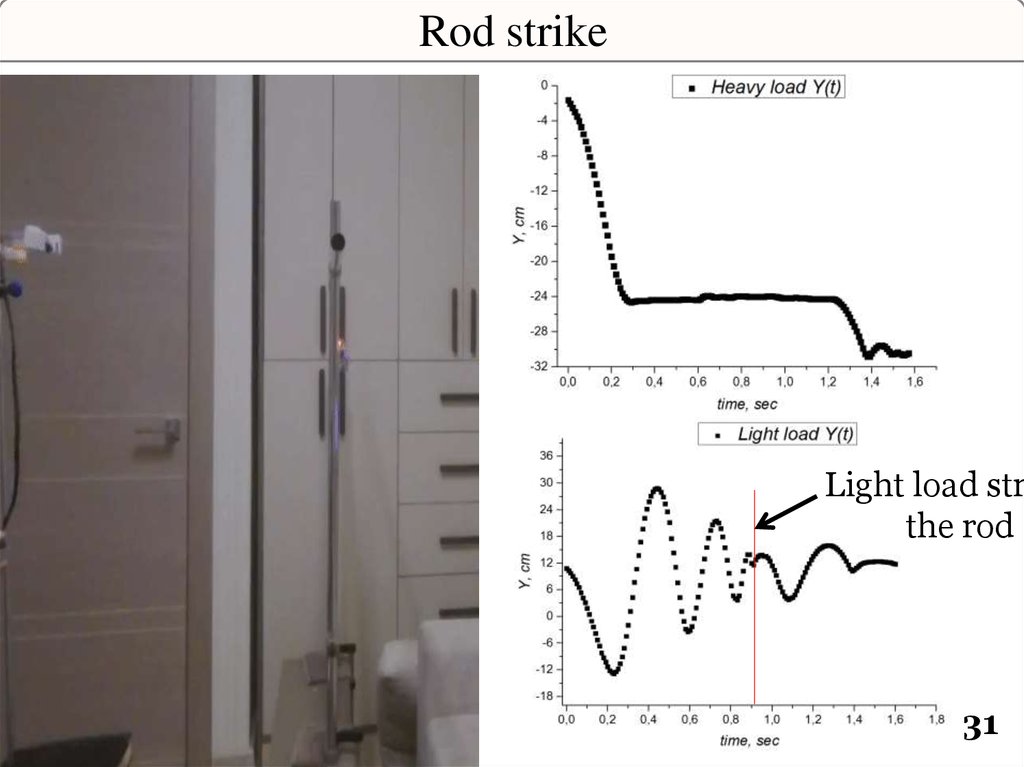
31.

Rod strike
Light load str
the rod
31

32.

Numerical solution error
.
.
h dt
dt
Total error i
Total error i
Iteration error 3,4mm
Iteration error 0,03
Value 350mm
Value 3,33
Solution error 1%
Solution error 1%
32

33.

Setup scheme
Massive string №1
g
1 (0,80 0,02)
m
1 0,110 0,004
Massive string №2
Electronic scale
measurements error = 0,01g
g
2 (1,80 0,02)
m
2 0,100 0,004
linear density
of string
33

34.

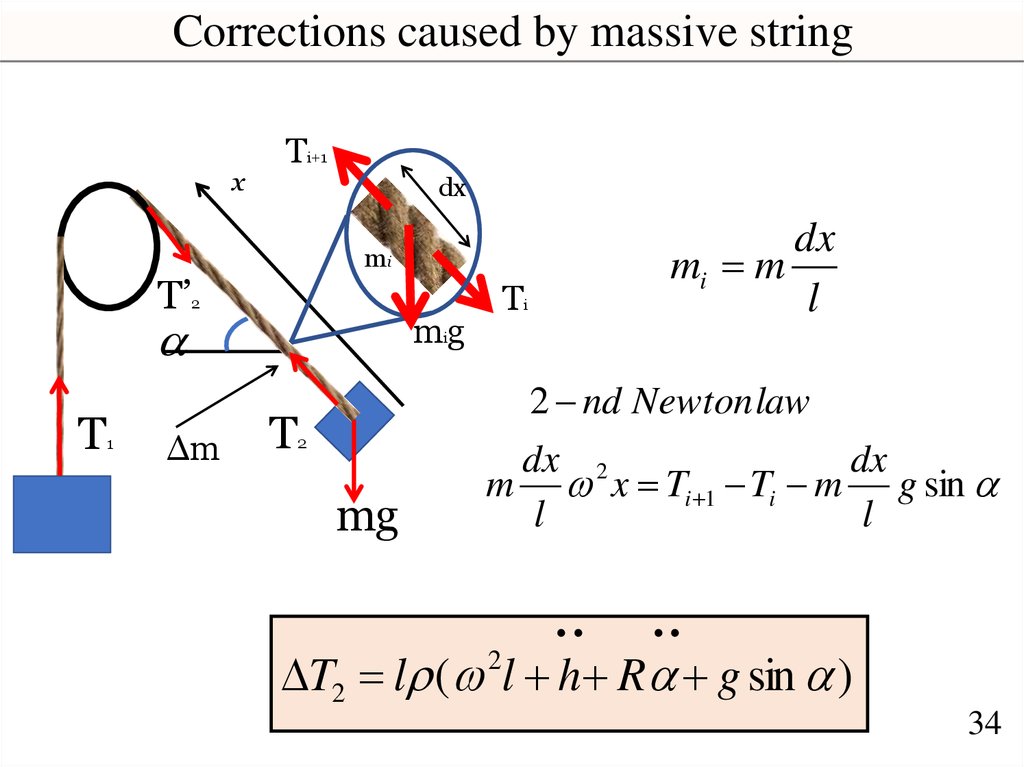
Corrections caused by massive string
x
T’
T
1
Ti+1
dx
mi
2
Δm
Ti
mig
dx
mi m
l
2 nd Newton law
T
2
mg
dx 2
dx
m x Ti 1 Ti m g sin
l
l
.. ..
T2 l ( l h R g sin )
2
34

35.

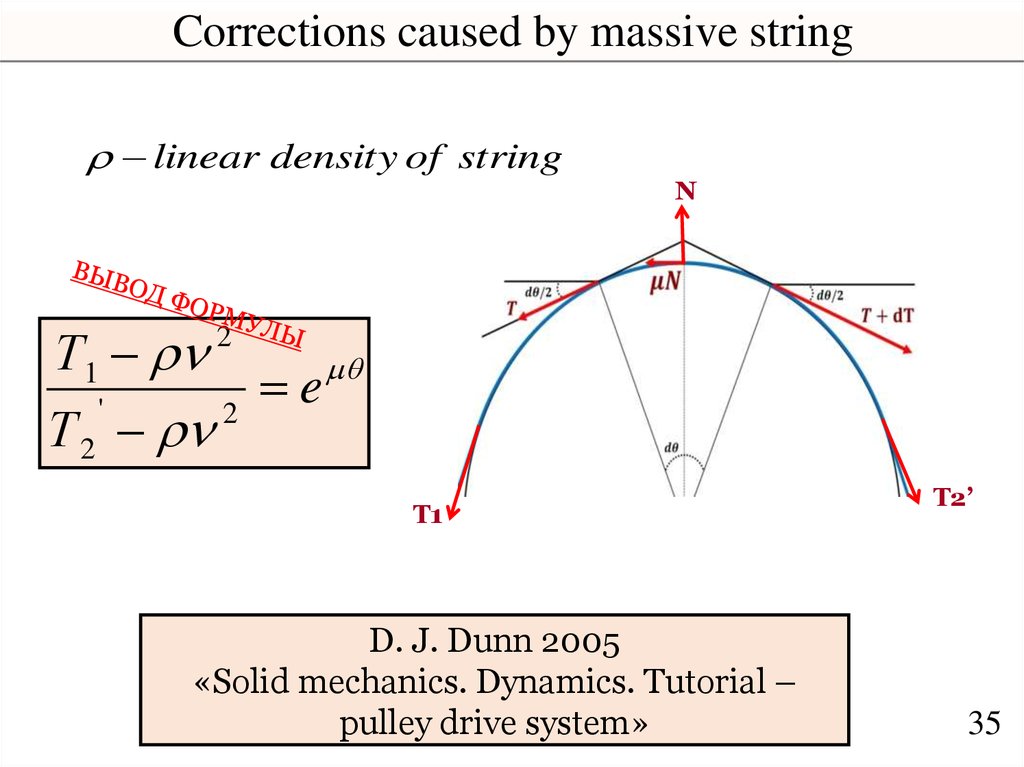
Corrections caused by massive string
linear density of string
N
Т1
e
'
2
Т 2
2
T1
D. J. Dunn 2005
«Solid mechanics. Dynamics. Tutorial –
pulley drive system»
T2’
35

36.

Correction in Euler’s formula caused by massive string
Y axis : N d v 2 Td
y
d
d
X axis : T dT cos
T cos
F fric 0
2
2
N
x
N Td d v 2
dT F fric N
dT d T v 2
TL
Т1
e
'
2
Т 2
2
TH
linear density of string
36

37.

Comparing theory with experiment for massive string
The theory agrees with the experiment!
The greater the mass of the thread, the
smaller the value of X
37

38. Swinging heavy load

Light load trajectory
Heavy load Y(t)

39.

3 - dimensional movement
Ffr 2
TH
T cos
12
T
F fr1
T sin
TL
In all other exp eriments
5 cos(5 ) 0.996 1
x
2 nd Newton law in
projection on x axe :
Maximal angle φ can be
predicted very well Z
Qualitative explanation
Th (1 e
2
) cos 2 2 max Th e
2
sin max
sin maxMainly
0.17problem
max can
11 be
solved as
2-dimensional
Quantitative model
Parametric investigation
39