Похожие презентации:
Обратное Z - преобразование
1.
ОбратноеZ - преобразование.
Цель: научиться восстанавливать
оригинал по известному Zизображению
2.
Задача восстановления оригиналапо известному изображению
решается при помощи обратного
Z-преобразования:
1
n 1
x (nT )
X ( z )z dz
2 j
3.
способы нахождения обратного zизображения:• с использованием таблицы
соответствий
• разложение на простые дроби
• на основании теоремы Коши о
вычетах
4.
Пример 1: дано Z-изображениеX(z) 0,5z
1
0,2z
2
0,8z
4
0,1z
5
Найти: дискретный сигнал.
т.к. Z изображение представлено
в виде суммы , то дискретный сигнал :
x(nT ) 0 ; 0,5 ; 0,2 ; 0 ; 0,8 ; 0,1
5.
Если Z-изображение дискретногосигнала представлено в виде дроби,
то необходимо привести его к виду:
X( z )
Xm z
m
m 0
- численный метод (деление
полинома числителя X(z) на
знаменатель)
6.
Пример 2: дано Z-изображениеX(z)
3
5z 2z 1
3
z 1
Найти: дискретный сигнал.
Решение: разделим полином
числителя на полином знаменателя
7.
35z 2z 1 z3 1
3
2
3
5
5z 5
5 2z 4z 2z
2z 4
2
2z 2z
2
4 2z
3
4 4z
2
3
2z 4z
2
5
2z 2z
8.
тогдаX( z )
3
5z 2z 1
5 2z
3
z 1
2
4z
3
2z
5
...
x(nT) 5; 0; 2; 4; 0; 2...
9.
• использование теоремы о вычетахесли
Q
W(z)
Ak
X(z) z
z
V(z)
k 0 z zk
где zk полюс X(z)
W(z)
Аk lim z zk
z zK
V(z)
тогда x(nT)
Q
Ak zk
k 0
n
10.
Пример 3: дано Z-изображениеX( z )
2
z 0,6z 0,08
2
z 0,8z 0,15
Найти: дискретный сигнал.
11.
Решение: приведем X(z) к видуW(z)
z2 0,6z 0,08
X( z ) z
z
V(z)
z z2 0,8z 0,15
Найдем полюса X(z):
2
z z 0,8z 0,15 0
z1 0; z2 0,5; z3 0,3
тогда:
2
z 0,6z 0,08
X( z ) z
z z 0,5 z 0,3
12.
Найдем коэффициенты Аk :2
z 0,6z 0,08
A1 lim z 0
z 0
z z 0,5 z 0,3
0,08
0,533
0,15
2
z 0,6z 0,08
A2 lim z 0,5
z 0,5
z z 0,5 z 0,3
0,03
0,3
0,1
13.
2z 0,6z 0,08
A2 lim z 0,3
z 0,3
z z 0,5 z 0,3
тогда
0,01
0,167
0,06
0,3
0,16
0,533
X( z ) z
z 0,5 z 0,3
z
0,3
0,16
0,533
1
1
1 0,5 z
1 0,3 z
14.
X(z) 0,5330,3
1 0,5 z
1
0,16
1 0,3 z
1
тогда дискретный сигнал
x(nT) 0,533 0 0,3 0,5 0,16 0,3
n
n
n
найдем первые три отчета ДС:
x(0T) 0,533 0 0,3 0,5 0,16 0,3
0
0
0
0,993
x(1T) 0,3 0,5 0,16 0,3 0,198
1
1
x(2T) 0,3 0,5 0,16 0,3 0,089
2
2
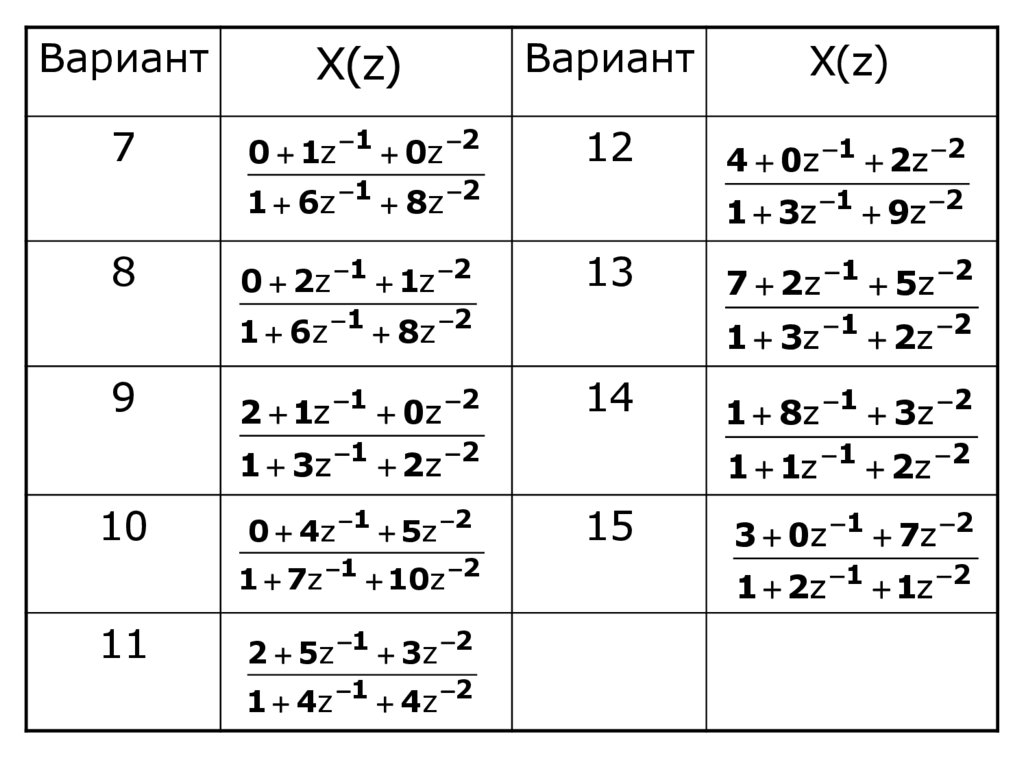
15. Практическое занятие
Задача 1Дано Z-изображение, найти дискретный сигнал
Вариант
1
2
3
4
X(z)
1
3 1z
2 3z
1
4 3z
1
2z
1z
2
2
3z
2
3z
2z
3
3
2z
3
3 1z 1 3z 2 2z 3
1
2
3
5
2 1z
6
1 2z 1 2z 2 4z 3
1z
0z
16.
ВариантX(z)
7
2 1z 1 1z 2 4z 3
8
1 1z 1 2z 2 4z 3
9
0 1z 1 2z 2 5z 3
10
2 0z 1 1z 2 2z 3
11
3 1z 1 4z 2 2z 3
12
8 4z 1 3z 2 3z 3
13
7 2z 1 3z 2 5z 3
14
6 1z 1 8z 2 4z 3
15
9 3z
1
2z
2
7z
3
17.
Задача 2Дано Z-изображение, найти
дискретный сигнал двумя способами
Вариант
1
X(z)
1 7z 1 1z 2
Вариант
X(z)
4
4 0z 1z 2
1 3z 2z 2
1 4z 1 3z 2
2
1 0z 1 2z 2
5
1 4z 1 3z 2
1 4z 1 3z 2
3
1 1z 1 1z 2
1 4z 1 3z 2
1 0z 1 4z 2
6
1 2z 0z 2
1 3z 1 2z 2
18.
ВариантX(z)
Вариант
X(z)
7
0 1z 1 0z 2
12
4 0z 1 2z 2
1 6z 1 8z 2
8
0 2z 1 1z 2
1 3z 1 9z 2
13
1 6z 1 8z 2
9
2 1z 1 0z 2
1 3z 1 2z 2
14
1 3z 1 2z 2
10
0 4z 1 5z 2
1 7z 1 10z 2
11
2 5z 1 3z 2
1 4z 1 4z 2
7 2z 1 5z 2
1 8z 1 3z 2
1 1z 1 2z 2
15
3 0z 1 7z 2
1 2z 1 1z 2






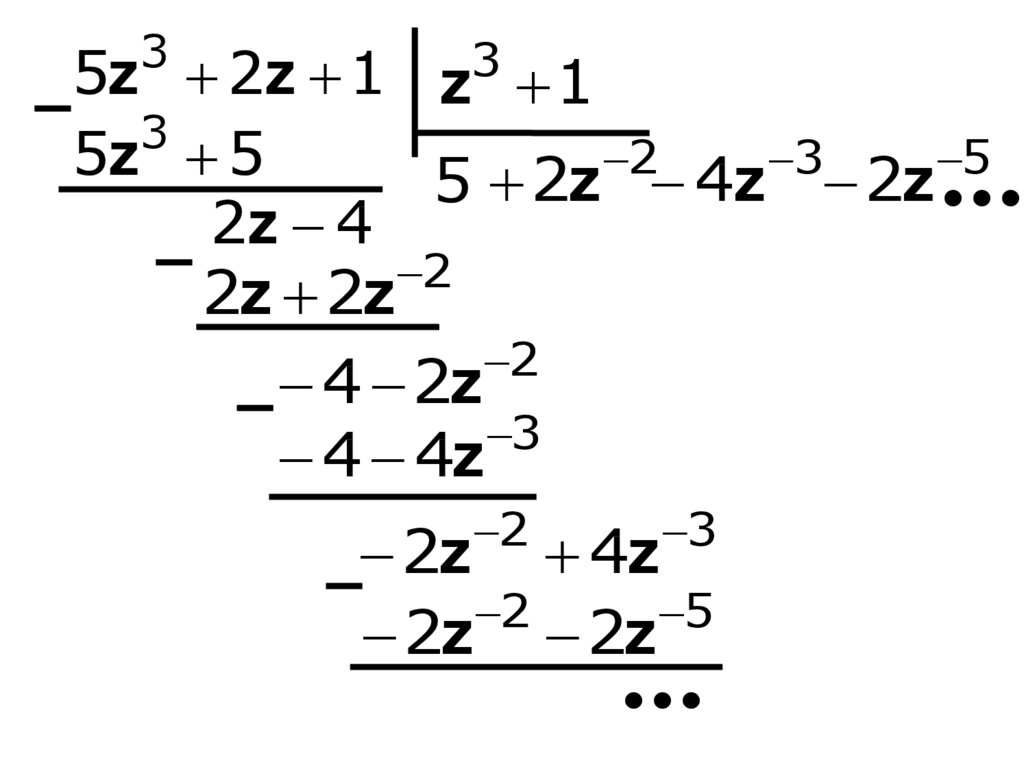










 Математика
Математика








