Похожие презентации:
Геометрический и физический смысл производной
1.
Мерзлякова Оксана АлександровнаУчитель высшей категории
МБОУ СОШ № 49
г. Краснодар
2012 г.
2.
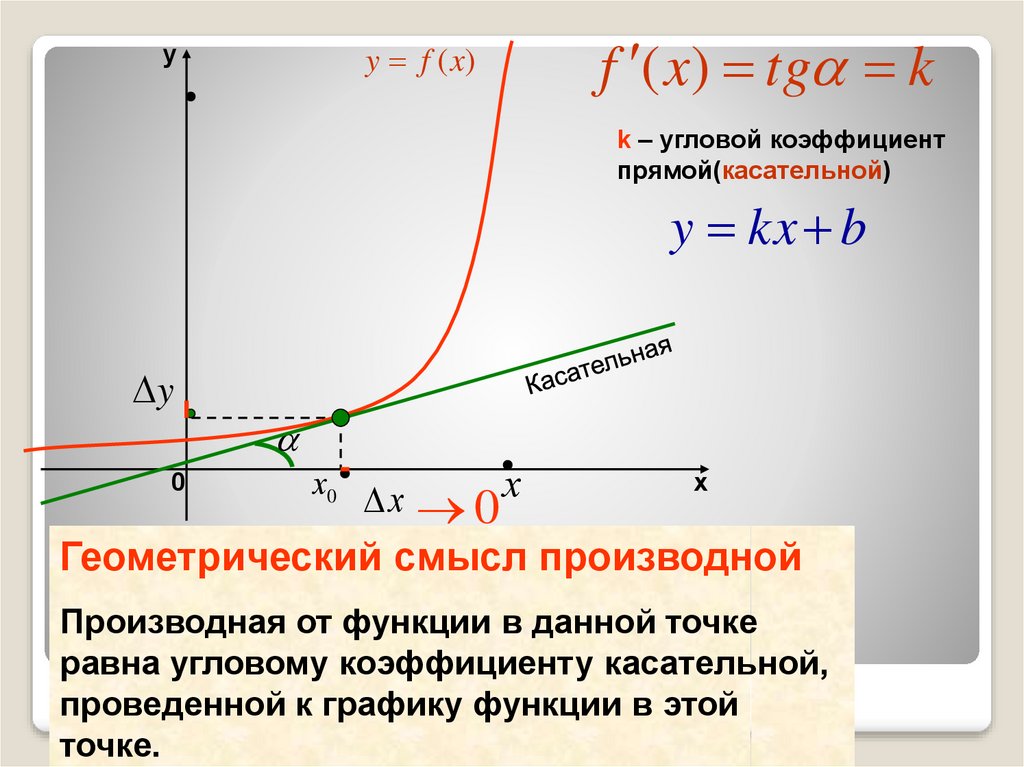
f ( x) tg ky f (x)
y
k – угловой коэффициент
прямой(касательной)
y kx b
y
0
х0
х
0
х
х
Геометрический смысл производной
Производная от функции в данной точке
равна угловому коэффициенту касательной,
проведенной к графику функции в этой
точке.
3.
для дифференцируемых функций : 0° ≤ α ˂180°, α ≠ 90°α = 90°
tg α не сущ.
f ´(x₃) не сущ.
α - тупой
tg α < 0
f ´(x₀) < 0
α – острый
tg α >0
f ´(x₁) >0
α=0
tg α =0
f ´(x₂) = 0
4.
Физический смысл производной функциив данной точке
х
Vср.
t
Или, если х перемещение тела, а t промежуток времени ,
в течении которого выполнялось движение, то
х
средняя скорость движения на промежутке времени t.
t
При t 0 Vcр. к мгновенной скорости V (t ),
следовательно, V (t ) S (t ).
S (t ) V (t )
или х (t ) V (t )
Производная от функции в данной точке это
скорость изменения функции .
f ( х) V ( x)
.
5.
формулы изфизики и
экономики, где
используется
производная.
υ(t) = х/(t) – скорость
a (t)=υ/ (t) - ускорение
J (t) = q/(t) - сила тока
C(t) = Q/(t) - теплоемкость
d(l)=m/(l) - линейная плотность
K (t) = l/(t) - коэффициент линейного расширения
ω (t)= φ/(t) - угловая скорость
а (t)= ω/(t) - угловое ускорение
N(t) = A/(t) - мощность
П (t) = υ / (t) - производительность труда,
где υ (t) - объем продукции
J(x) = y / (x) - предельные издержки производства,
где y– издержки производства в зависимости от объема выпускаемой
продукции x.
6. Решите задачи.
1 Найдите угловой коэффициенткасательной, проведенной к графику
функции у=9 -4х в его точке с
абсциссой х = 1.
2. Найдите тангенс угла наклона
касательной, проведенной
к графику
3
функции в его точке с абсциссой .
Решите задачи.
y 0,5x 2
x0 3
7. Найти соответствие между функцией и её производной.
8.
1. Пусть Q (t) количество теплоты,которое необходимо для нагревания
тела массой 1 кг от 00С до температуры
t0 (по Цельсию), известно, что в
диапазоне 00 <= t <= 950, формула
Q (t) = 0,396t+2,081 10-3t2-5,024 10-7t3
дает хорошее приближение к истинному
значению. Найдите, как зависит
теплоёмкость воды от t.
9.
7. Высота снежка, брошенноговертикально вверх со скоростью U0 с
начальной высоты h0, меняется по
закону h =h0+U0*t-gt2/2, где g » 10м/c –
ускорение силы тяжести. Покажите, что
энергия камня Е=тv2/ 2 + mgh, где т –
масса снежка, не зависит от времени.
10.
6. Количество электричества,протекающее через проводник,
задаётся формулой а) q(t) = t- 3t3/2+1:
б) q(t) = t+4/t. В какой момент времени
ток в цепи равен нулю?
11. 3. Определите абсциссы точек, в которых угловой коэффициент касательной к графику функции равен 2.
h( x) 1 2 sin 2 xy f (x)
4. На рисунке изображен график
производной . Найдите точки минимума
функции .
y f (x)
3. Определите абсциссы точек, в которых
угловой коэффициент касательной к графику
функции
равени2.
5. Найдите скорость
ускорение изменения функции
y x3 5 x 4
в точке х = 5
12.
6. Найдите производную функции h( x) sin x 3x 4 5В точке x0 = /2
7. Найдите значение производной
x0
функции
в точке
y f (x)
13. Найти наименьшее значение функции
14. Домашнее задание
Повторить теорию : пункт 28,29№ 29.8, 29.21
Домашнее задание













 Математика
Математика








