Похожие презентации:
Что должен знать ученик о способах задания функции? Какие достоинства и недостатки имеет каждый способ?
1. 8. Что должен знать ученик о способах задания функции? Какие достоинства и недостатки имеет каждый способ?
2.
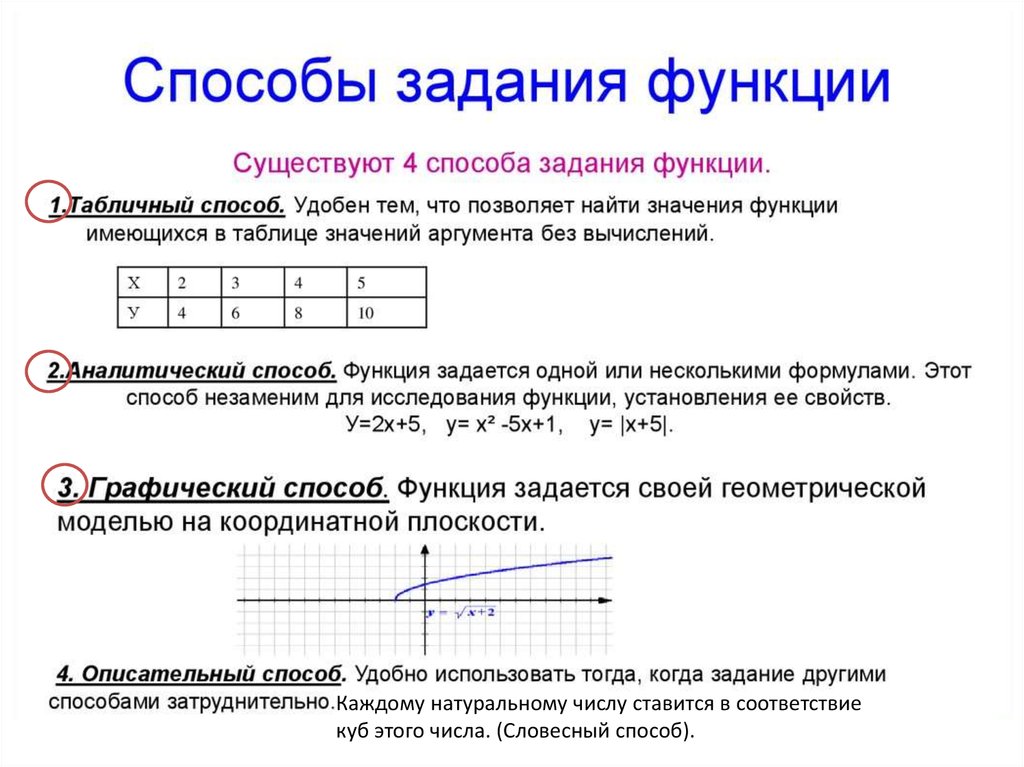
Каждому натуральному числу ставится в соответствиекуб этого числа. (Словесный способ).
3. Подведение к теме
Что мы знаем о функции? Определение. Область определения, областьзначения, график функции.
Дайте определение
функции
Функция – это правило, по которому каждому
значению х из некоторого множества
соответствует единственное значение у из
другого множества.
Что мы еще знаем о
функции?
Область определения, область значения,
график функции.
Что такое область
определения функции?
Область определения функции - это
множество всех тех значений х, при которых
функция имеет смысл.
Что называется областью Область значений функции – это множество
значений функции?
всех тех значений у, которые принимает
функция.
4.
Прежде чем говорить о функции,необходимо ее задать.
Задать функцию, значит указать некоторое
правило, которое позволяет произвольно
выбранному значению х из D(f) найти
соответствующее значение у.
5.
Если правило задается формулой илинесколькими формулами – такой способ
задания функции называется
аналитическим.
Пример: у=2х+1
В чем главный смысл аналитического
способа задания функции?
Задаем непосредственную формулу для
нахождения переменной у.
6.
• Что значит задать функцию графически?• Значит, задать график некоторой функции.
(у=2х+1)
7.
• Третий способ, каким можно задатьфункцию – табличный способ.
• Т.е. указать таблицу значений, которые
функция может принимать.
• у=2х+1
8.
• Четвертый способ, словесный. Чем онхарактеризуется?
• Этот способ состоит в том, что
функциональная зависимость выражается
словами.
• Например: Функция у = f(x) задана на
множестве однозначных натуральных чисел с
помощью следующего правила: каждому
числу х ставится в соответствие удвоенное его
значение. у=2х
9.
• Более того, словесно можно задать функцию,которую формулой задать крайне
затруднительно, а то и невозможно.
Например: каждому значению натурального
аргумента х ставится в соответствие
сумма цифр, из которых состоит значение
х. Например,
если х=3, то у=3. Если х=257, то у=2+5+7=14. И
так далее. Формулой это записать
проблематично.
10. Связаны ли эти способы?
• Все примеры описывают одну и ту жефункцию у=2х+1, которая имеет график и
все значения, которые указанны в таблице
лежат на прямой.
• Т.о. в зависимости от заданий, всегда
можно использовать любую из этих форм.
11.
ДостоинстваНедостатки
1 Табличн Дает числовое значение
ый
функции.
В этом его преимущество
перед другими способами
Таблица трудно обозрима в
целом; она часто не содержит
всех нужных значений
аргумента.
2 Аналити Всегда можно вычислить
ческий точно значение для
любого аргумента.
По самой формуле сложно
понять общее поведение
функции.
3 Графиче Легкость обозрения в
ский
целом и непрерывность
изменения аргумента
Ограниченная степень точности
и утомительность
«прочитывания» значений
функции с максимально
возможной точностью
4 Описате Возможность задания тех
льный
функций, которые не
удается выразить
аналитически
Невозможность вычисления
значений функции при
произвольном значении
аргумента и отсутствие
наглядности
12.
12
3
4
В
Г
А
Б











 Математика
Математика








