Способы задания функции

1.

2.

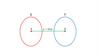
1. Для каждого графика укажите D(f) и E(f):
D( f ) 3; 1
E ( f ) 2; 4
D( f ) 3; 2
E ( f ) 1; 5
D( f ) 4; 2 1; 3
E ( f ) : 2; 2.

3.

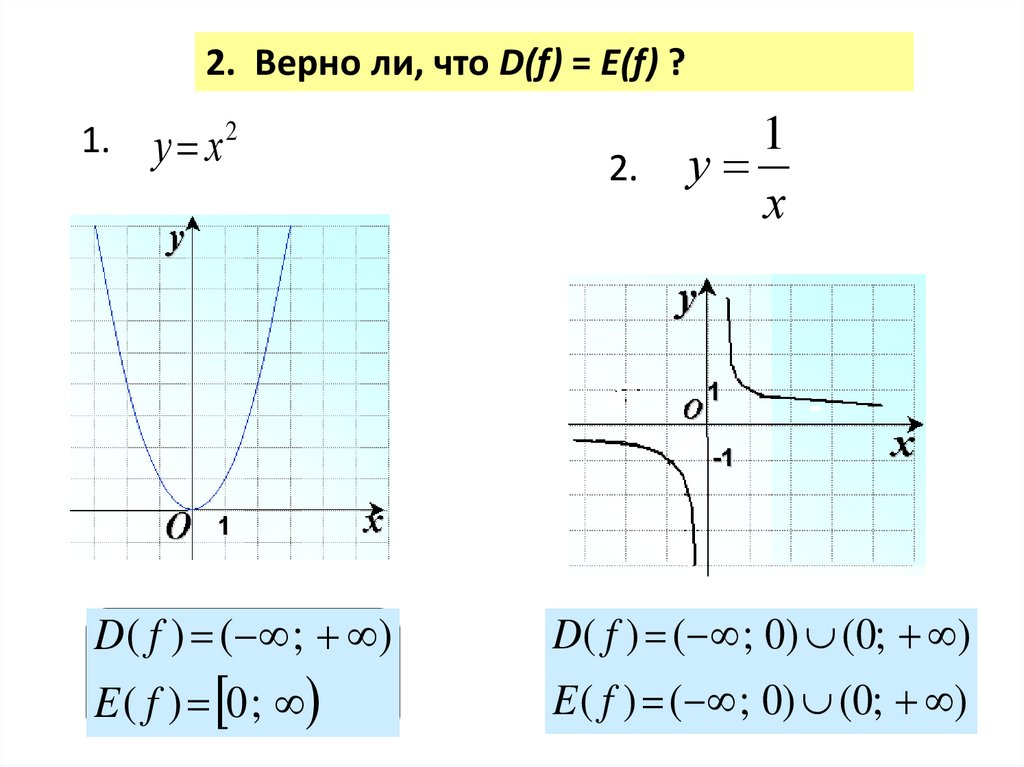
2. Верно ли, что D(f) = E(f) ?
1.
у х
2
D( f ) ( ; )
E ( f ) 0 ;
2.
1
у
х
D( f ) ( ; 0) (0; )
E ( f ) ( ; 0) (0; )

4.

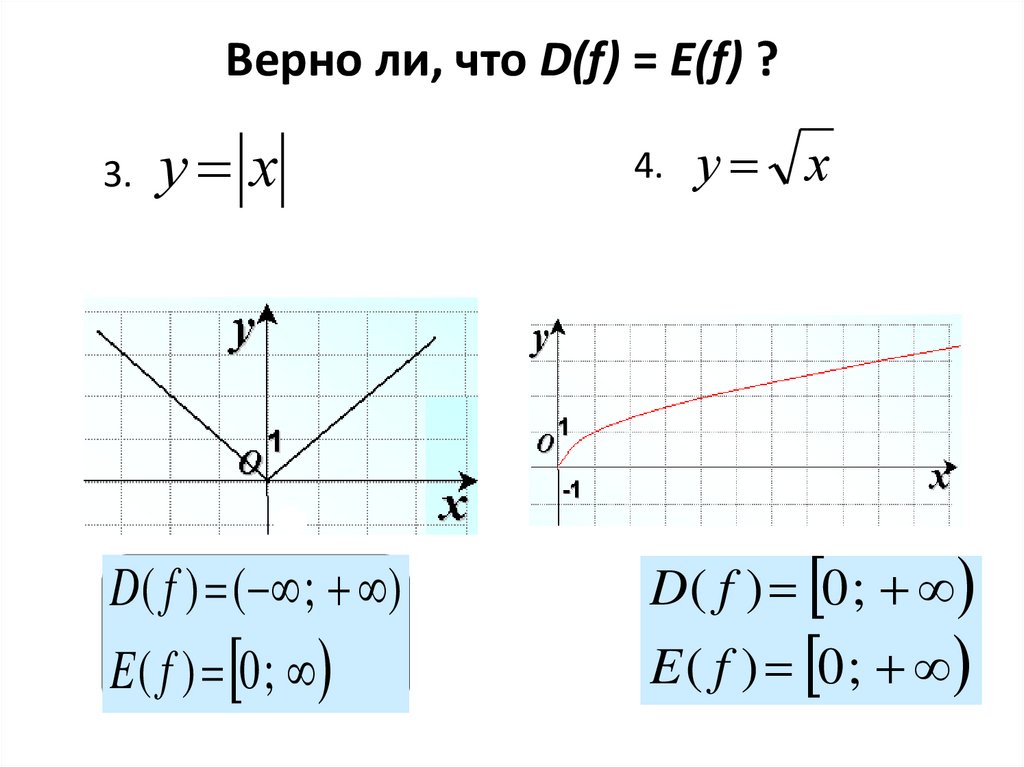
Верно ли, что D(f) = E(f) ?
3.
у х
D( f ) ( ; )
E ( f ) 0 ;
4.
у х
D( f ) 0 ;
E ( f ) 0 ;

5.

2. Укажите область определения функции.
х 1
у
( х 2)( х 3)
у х 3х 4
2
у
х
х 2
D( f ) : x 2; x 3
D( f ) ( ; )
D( f ) ; 0 2;

6.

Указать правило, которое позволяет
произвольно выбранному значению х
из D(f) найти соответствующее
значение у.

7.

Аналитический способ задания
функции
Если правило
связано с формулой или несколькими формулами –
то такой способ задания функции называется аналитическим.
у2 х 9
x 2 , если х 0,
f ( x)
х 3, если х 0.
2
у 2х 3
x 2 , если х 2,
f ( x)
2 x 3, если х 0.
нет. у 9 х
да
да
нет, ( ; 2) (0 ; ) (0; 2

8.

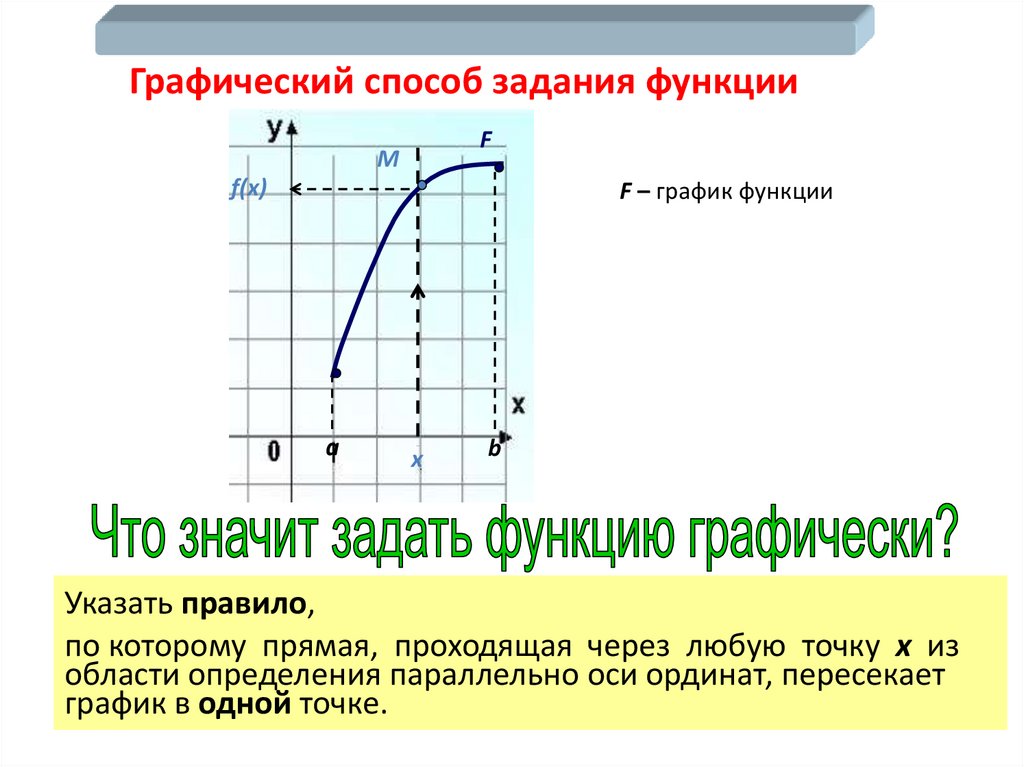
Графический способ задания функции
F
М
f(x)
F – график функции
a
x
b
Указать правило,
по которому прямая, проходящая через любую точку х из
области определения параллельно оси ординат, пересекает
график в одной точке.

9.

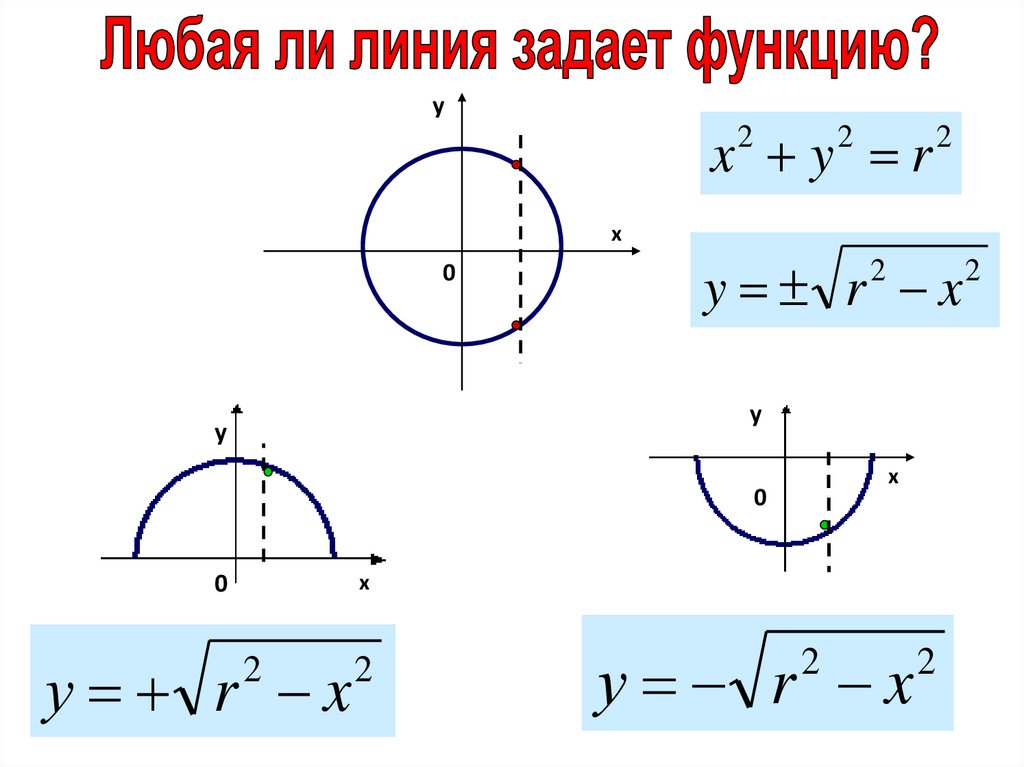
у
x y r
2
2
2
x
0
y r x
2
у
у
x
0
x
0
у r x
2
2
у r x
2
2
2

10.

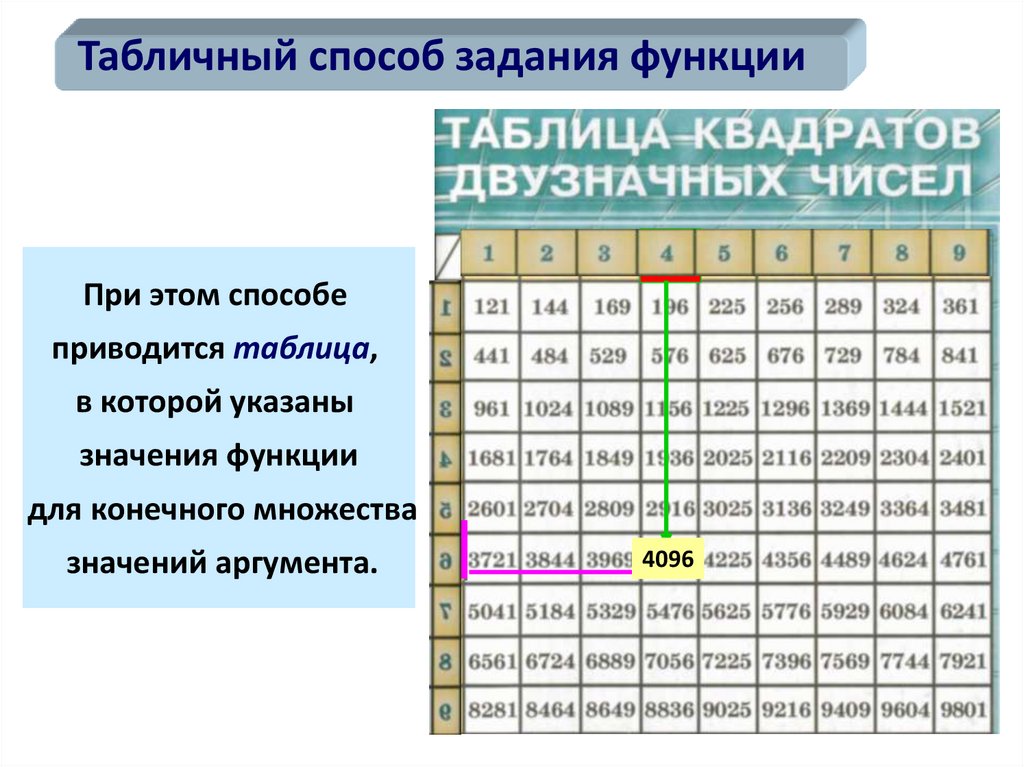
Табличный способ задания функции
При этом способе
приводится таблица,
в которой указаны
значения функции
для конечного множества
значений аргумента.
4096

11.

Словесный способ задания функции
– когда правило задания функции
описывается словами.
№ 1. Функция у = f(x) задана на множестве
однозначных натуральных чисел с помощью следующего
правила: каждому числу х ставится в соответствие
удвоенное его значение.
x
1
2
3
4
5
6
7
8
9
f(x)
2
4
6
8
10
12
14
16
18

12.

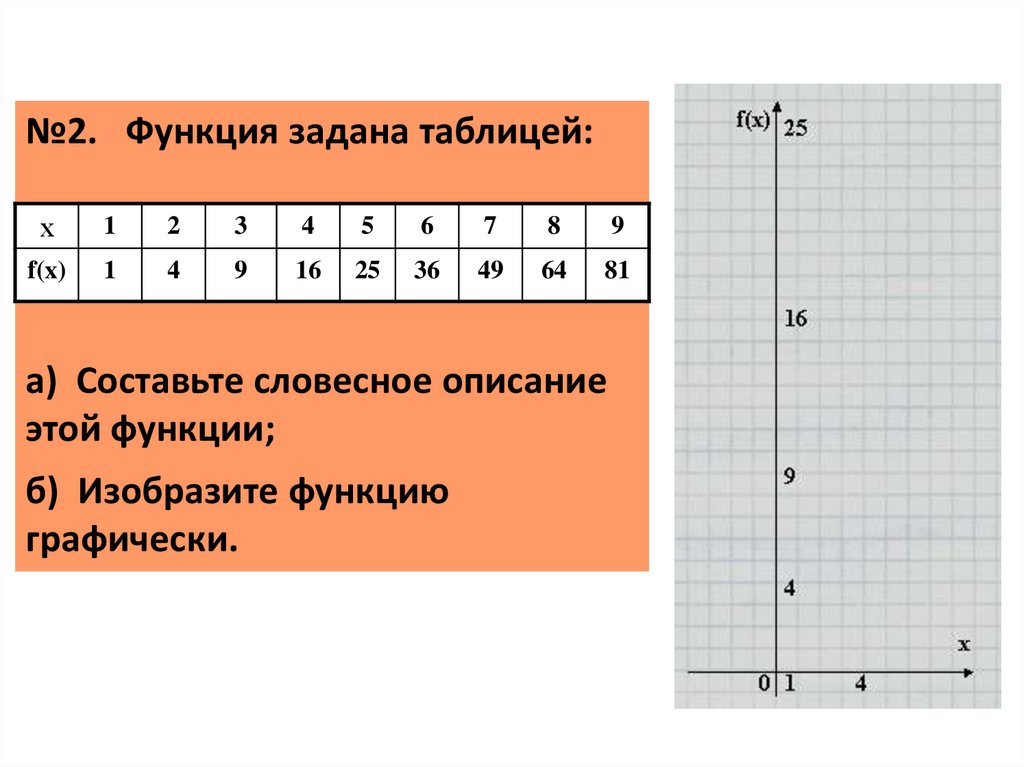
№2. Функция задана таблицей:
х
1
2
3
4
5
6
7
8
9
f(x)
1
4
9
16
25
36
49
64
81
а) Составьте словесное описание
этой функции;
б) Изобразите функцию
графически.

13.

1. Аналитический
2. Графический
3. Табличный
4. Словесный
1. Знать D(f) .
2. Указать правило, которое позволяет произвольно выбранному
значению х из D(f) найти соответствующее значение у.