Похожие презентации:
Динамика точки. Основные законы современной механики
1.
2.
ДИНАМИКА –наиболее общий раздел механики,
в котором изучается
движение материальных тел
в зависимости
от действующих на них сил
3.
Основные законысовременной механики
Ньютон сформулировал в
своей книге
«Математические начала
натуральной философии»
4. Галилео Галилей (1564–1642)
Итальянский физик,механик,
астроном, философ
и математик.
Основатель
экспериментальной
физики
5. Исаак НЬЮТОН (1643 – 1727)
Английский физик иматематик,
создатель
теоретических основ
механики и
астрономии
6. Жозеф Луи Лагранж (1736-1813)
Французскийматематик и
механик,
создатель
аналитической
механики
7. 1. Закон инерции
Открыт Галилеем в 1638 г. :«Изолированная от внешних
воздействий материальная точка
сохраняет свое состояние покоя
или равномерного прямолинейного
движения до тех пор, пока
приложенные силы не заставят ее
изменить это состояние»
8. 2. Основной закон механики (второй закон Ньютона)
«Изменение количествадвижения пропорционально
приложенной силе и происходит по
направлению той прямой, по которой
эта сила действует»
(формулировка Ньютона)
m(v v0 ) P(t t0 )
9.
Формулировка Эйлера:(v v0 )
P m lim
ma
t 0 (t t )
0
Современная запись:
ma P
10.
Система отсчета,в которой проявляются
первый и второй законы,
называется
инерциальной
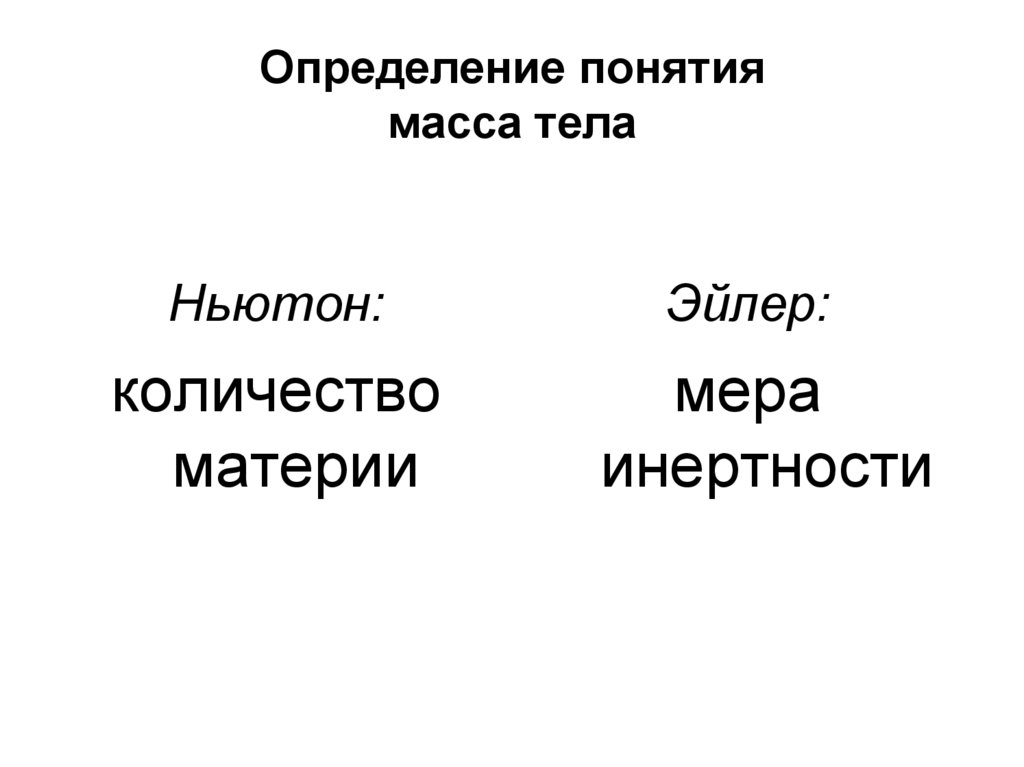
11. Определение понятия масса тела
Ньютон:количество
материи
Эйлер:
мера
инертности
12. 3. Закон равенства действия и противодействия:
«Всякомудействию
соответствует равное и
противоположно
направленное
противодействие»
13. 4. Закон независимости действия сил
«Несколько одновременно действующихна материальную точку сил
сообщают точке такое ускорение,
которое сообщила бы ей одна сила,
равная их геометрической сумме»
ma Pi R
14. Дифференциальные уравнения движения материальной точки в декартовых координатах
ma Pi RПроектируем обе части равенства на координатные оси
max X i ;
i 1
n
ma y Yi ;
i 1
n
maz Z i .
i 1
n
d 2x n
m 2 X i ;
dt
i 1
d2y n
m 2 Yi ;
dt
i 1
2
n
d z
m 2 Zi .
dt
i 1
Дифференциальные
уравнения
движения
материальной точки
15. Дифференциальные уравнения движения материальной точки в естественных координатах
ma Pi RПроектируем обе части равенства на естественные оси
ma F ;
i 1
n
man Fn ;
i 1
n
mab Fb .
i 1
n
d 2s n
m 2 F ;
dt
i 1
n
v2
m Fn ;
i 1
n
m 0 Fb 0
i 1
Дифференциальные
уравнения
движения
материальной точки
16. Задачи динамики
Первая –зная массу точки m
и уравнения ее
движения
x f1(t ); y f 2 (t); z f3 (t )
найти модуль и
направление
равнодействующей
сил,
приложенных к точке
Вторая –
зная силы,
действующие на
материальную
точку,
начальное положение
точки и ее
начальную скорость,
получить уравнения
движения точки
17. Первая задача динамики
зная массу точки и уравнения ее движения,найти модуль и направление равнодействующей сил, приложенных к точке
x f1(t );
d x
X m 2 ;
dt
2
d y
Y m 2 ;
dt
2
d z
Z m 2 .
dt
2
y f 2 (t );
P
z f3 (t )
X Y Z ;
2
2
cos( P , i ) X / P;
cos( P , j ) Y / P;
cos( P , k ) Z / P
2
18. Вторая задача динамики
зная силы, действующие наматериальную точку,
начальное положение точки
и ее начальную скорость,
получить уравнения движения точки
19.
20. Общие теоремы динамики точки
Устанавливают наглядные зависимости междуосновными динамическими характеристиками
движения материальных тел.
Избавляют от необходимости проделывать для
каждой задачи те операции интегрирования,
которые раз и навсегда производятся при
выводе этих теорем.
21. Меры механического движения:
1. Количество движения – векторнаявеличина, равная произведению
массы точки m на скорость v:
Q=mv
В системе СИ единица измерения
кгм/сек
22. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ –
скалярная величинаmv 2
T
,
2
равная половине произведения массы точки на
квадрат ее скорости.
В системе СИ единица измерения
кг м / сек н м джоуль
2
2
23. Теорема об изменении количества движения материальной точки
ma P ;dv
m
P;
dt
d (mv )
P.
dt
«Производная по времени
от количества движения
материальной точки
геометрически равна
сумме всех действующих на точку
сил»
24.
d (mv ) P dt. Интегрируемmv2 mv1 Si .
v2
t2
v1
t1
d (mv ) P dt.
В интегральной форме:
«Изменение
количества движения
материальной точки
за некоторый промежуток времени
равно геометрической сумме
импульсов сил,
приложенных к точке
за тот же промежуток времени»
25.
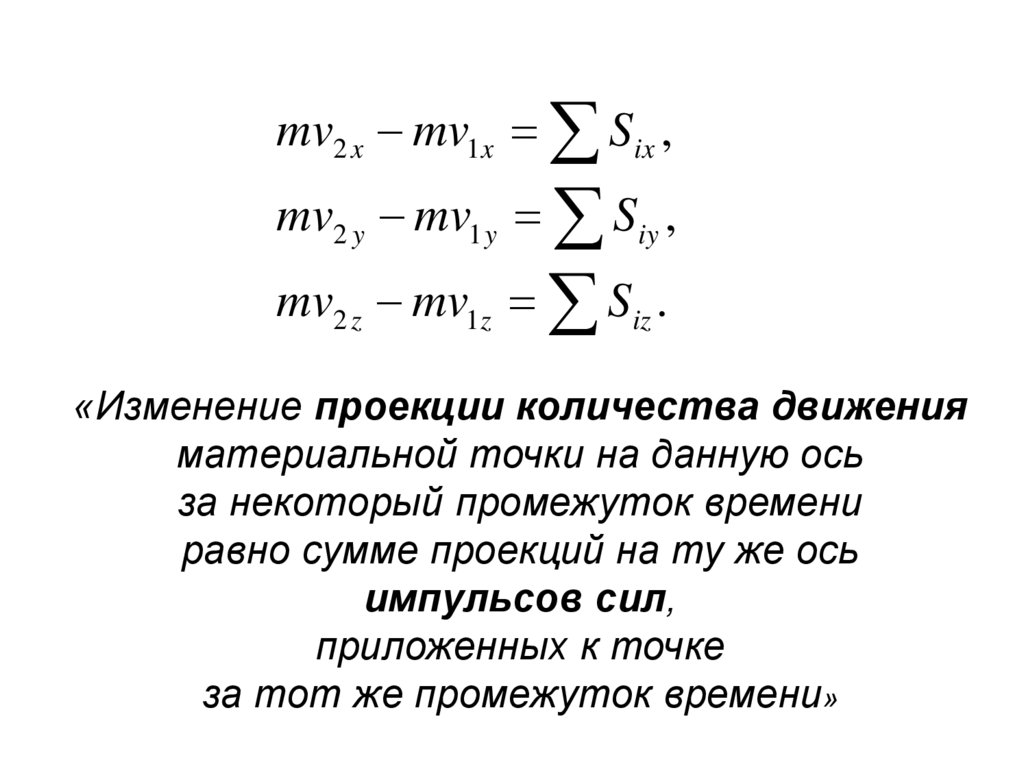
mv2 x mv1x Six ,mv2 y mv1 y Siy ,
mv2 z mv1z Siz .
«Изменение проекции количества движения
материальной точки на данную ось
за некоторый промежуток времени
равно сумме проекций на ту же ось
импульсов сил,
приложенных к точке
за тот же промежуток времени»
26. МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ ОТНОСИТЕЛЬНО ПОЛЮСА O –
момент количества движения точкиотносительно этого полюса:
LO r mv
где m масса точки,
v
– ее скорость,
r
– радиус–вектор.
27.
Теорема об изменении кинетического момента точкиотносительно полюса
LO r mv;
dLO d r mv dr
dv
mv r m
dt
dt
dt
v mv r ma 0 r R M O ;
dLO
MO
dt
dt
28.
Производная по времениот кинетического момента материальной точки
относительно некоторого неподвижного центра
равна моменту равнодействующей сил,
действующих на материальную точку,
относительно того же центра
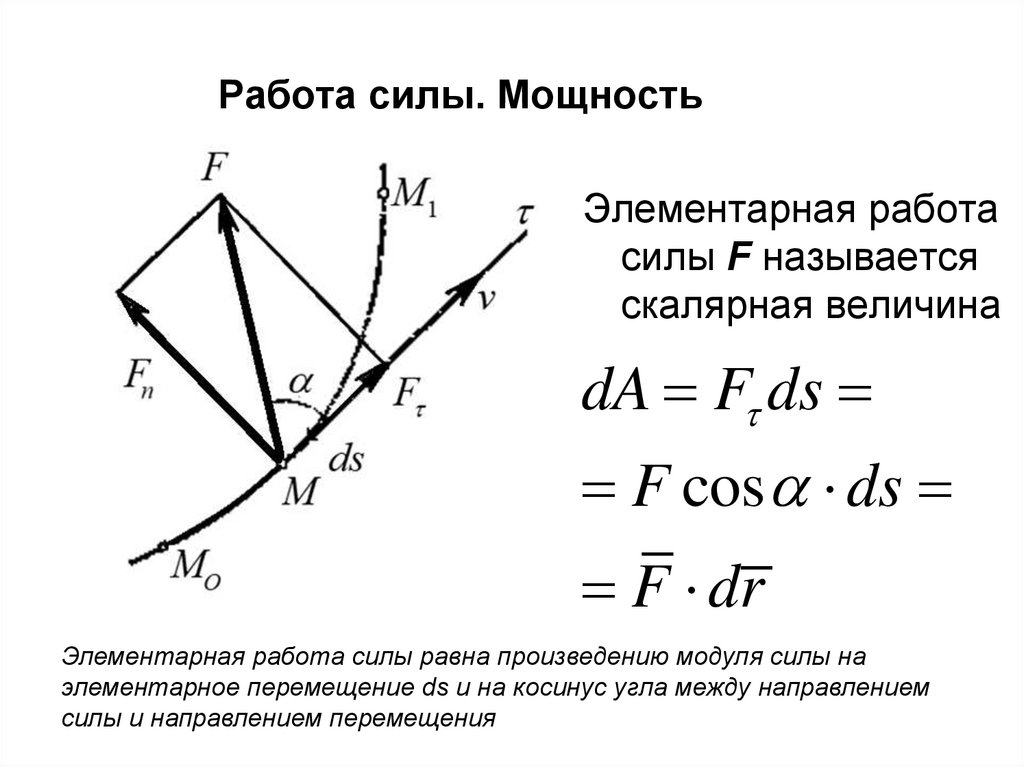
29. Работа силы. Мощность
Элементарная работасилы F называется
скалярная величина
dA F ds
F cos ds
F dr
Элементарная работа силы равна произведению модуля силы на
элементарное перемещение ds и на косинус угла между направлением
силы и направлением перемещения
30.
31. Аналитическое выражение элементарной работы
dA F dr ( Fx i Fy j Fz k ) (dx i dy j dz k )Так как i j i k j k 0,
а i i j j k k 1,
то dA Fx dx Fy dy Fz dz
32.
Работа силы на любом конечном перемещениивычисляется как интегральная сумма
соответствующих элементарных работ
и будет равна:
A( M 0 M1 )
( M1 )
(M0 )
F ds
( M1 )
( Fx dx Fy dy Fz dz )
( M0 )
Работа силы на любом перемещении М0М1
равна взятому вдоль этого перемещения
интегралу
от элементарной работы
Единицей измерения работы в системе СИ является джоуль
(1 дж=1Нм)
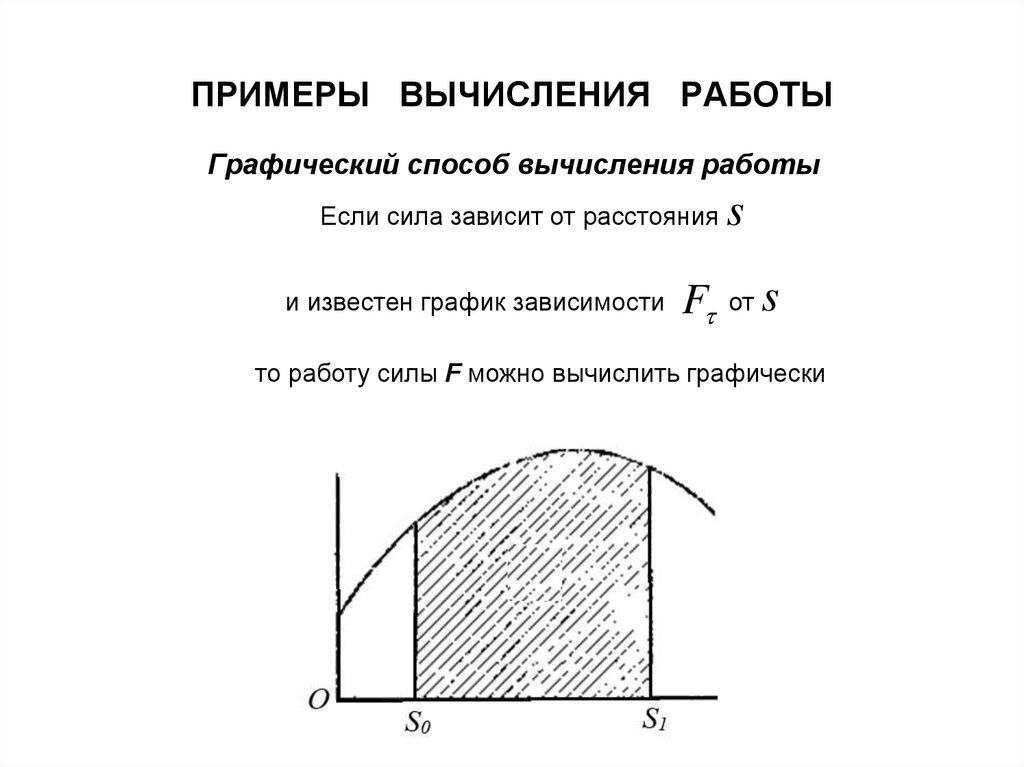
33. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ
Графический способ вычисления работыЕсли сила зависит от расстояния
и известен график зависимости
F
s
от
s
то работу силы F можно вычислить графически
34. Работа силы тяжести
A( M 0 M1 )( M1 )
z1
( P)dz P dz P ( z0 z1 ) Ph.
(M0 )
A( M 0 M1 ) Ph
z0
35.
Работа силы тяжести не зависитот вида той траектории,
по которой перемещается точка ее
приложения.
Силы, обладающие таким свойством,
называются потенциальными
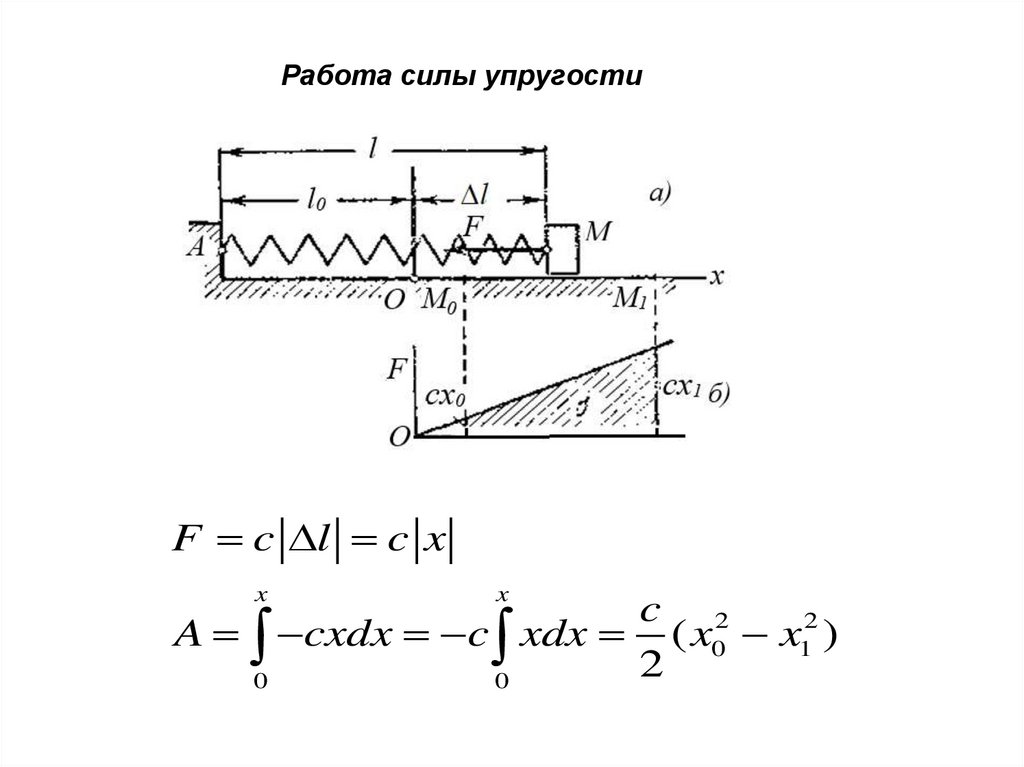
36. Работа силы упругости
F c l c xx
x
c 2
A cxdx c xdx ( x0 x12 )
2
0
0
37.
Работа силы упругости равнаполовине произведения коэффициента жесткости
на разность квадратов
начального и конечного удлинений (или сжатии)
пружины
38. Работа силы трения
A( M 0 M1 )( M1 )
(M0 )
Fтр ds
( M1 )
f N ds
(M0 )
Работа силы трения при скольжении
всегда отрицательна.
Величина этой работы зависит от длины дуги М0М1 ,
следовательно,
сила трения является
силой непотенциальной
39. Мощность
Мощность - величина, определяющаяработу, совершаемую силой в
единицу времени.
W dA
dt
F ds
dt
F v
Единицей измерения мощности в системе СИ является
ватт (1вт=1 дж/сек), а в системе МкГС—1 кГм/сек.
В технике за единицу мощности часто принимается 1
лошадиная сила, равная 75 кГм/сек или 736 вт.
40. Теорема об изменении кинетической энергии точки
ma Fia dv
dt
dv
ds
ds
dt
dv
dv
mv
Fi ; mvdv Fi ds;
ds
2
mv
d(
) Fi ds
2
ds
v
41.
21
2
0
mv
mv
A( M 0 M1 )
2
2
Изменение кинетической энергии точки при
некотором ее перемещении
равно алгебраической сумме работ
всех действующих на точку сил
на том же перемещении
42. Связи и их уравнения
Несвободной материальной точкойназывается точка, свобода движения
которой ограничена.
Тела, ограничивающие свободу движения
точки,
называются связями.
43.
Пусть связь представляет собойповерхность какого-либо тела,
по которой движется точка.
Тогда координаты точки должны удовлетворять
уравнению этой поверхности, называемому
уравнением связи
f ( x, y , z ) 0
44.
Если точка вынуждена двигаться по некоторой линии(движение шарика внутри криволинейной трубки),
то уравнениями связи
являются уравнения этой линии
f1 ( x, y, z ) 0;
f 2 ( x, y, z ) 0.
45.
Связи делятся на:а) односторонние, или неудерживающие;
б) двусторонние, или удерживающие.
46.
Уравнения неудерживающей связи выражаются неравенствами:x y z l 0
2
2
2
2
Уравнения удерживающей связи выражаются равенствами:
x y z l 0
2
2
2
2
47.
2dx d x
f ( x, , 2 , t ) 0
dt dt
Дифференциальные интегрируемые связи –
связи, выраженные дифференциальными
уравнениями,
которые могут быть проинтегрированы.
Связь называется голономной,
если она выражается или конечным соотношением
между координатами точки, т. е. уравнением, не
содержащим никаких производных от координат,
или интегрируемым дифференциальным уравнением.
48.
Если дифференциальное уравнение,выражающее связь,
неинтегрируемо,
т. е. его нельзя привести к некоторому эквивалентному
соотношению
f ( x, y , z , t ) C
только между координатами точки и t,
то эта связь называется
неголономной
49.
Голономные механические связи делятсяна:
1) Стационарные (равенства,
выражающие связи, не содержат явно
время);
2) Нестационарные (если в эти
равенства явно входит время).
50.
Пример нестационарной связиx y (l0 ut ) 0
2
2
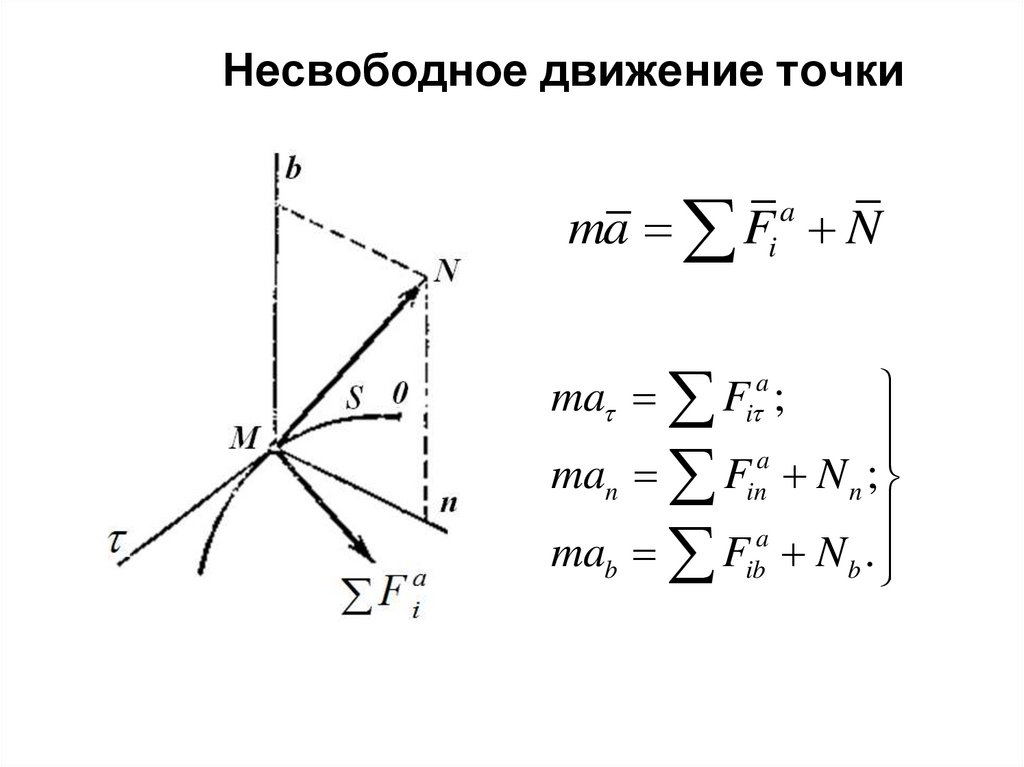
51. Несвободное движение точки
ma Fi a Nma Fi ;
a
man Fin N n ;
a
mab Fib N b .
a
52.
d sa
m 2 Fi ; (1)
dt
2
v
a
m Fin N n ; (2)
0 Fiba N b . (3)
2
Уравнение (1) не содержит неизвестной реакции N
и позволяет определить закон движения точки вдоль кривой,
т. е. зависимость s=f(t).
Уравнения же (2,3) служат для определения реакции связи
53. Принцип Даламбера:
«Если к заданным (активным) силам,действующим на точку, и реакциям
наложенных связей
присоединить силу инерции,
то получится уравновешенная система сил»
ma P N ; P N ma 0;
Pi Ni Фi 0
ma Ф;
54. Динамика относительного движения точки
55. Основной закон динамики относительного движения точки
«Все уравнения и теоремы механики дляотносительного движения точки
составляются так же,
как уравнения абсолютного движения,
если при этом к действующим на точку
силам взаимодействия с другими
телами прибавить переносную и
кориолисову силы инерции»
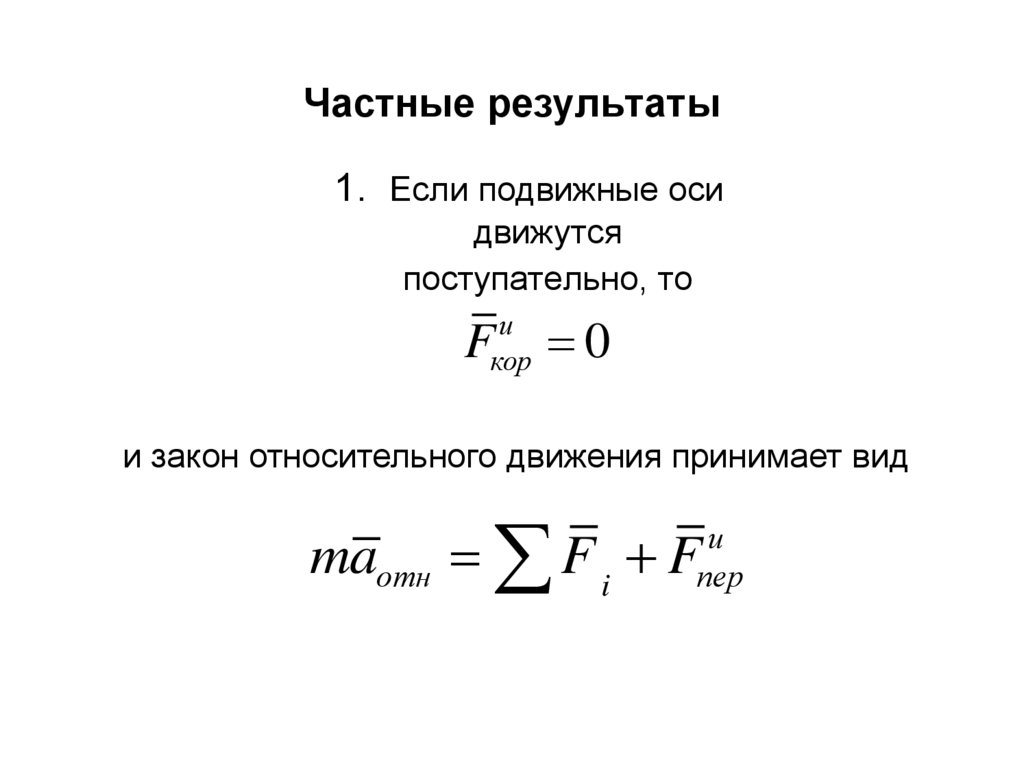
56. Частные результаты
1. Если подвижные осидвижутся
поступательно, то
и
кор
F
0
и закон относительного движения принимает вид
maотн F i F
и
пер
57.
2. Если подвижные оси перемещаютсяпоступательно, равномерно и прямолинейно, то
и
пер
F
F
и
кор
0
и закон относительного движения будет иметь
такой же вид,
как и закон движения
по отношению к неподвижным осям.
Следовательно,
такая система отсчета также будет
инерциальной
58. Принцип относительности классической механики (Галилей)
«Никаким механическим экспериментомнельзя обнаружить,
находится ли данная система отсчета
в покое
или совершает поступательное,
равномерное и прямолинейное
движение»
59.
3. Если точка по отношению к подвижным осямнаходится в покое, то для нее
aотн aкор vотн 0;
F
F
i
и
пер
0
Уравнения относительного равновесия
составляются так же,
как уравнения равновесия в неподвижных осях,
если при этом к действующим на точку силам
взаимодействия с другими телами
добавить переносную силу инерции
60.
икор
F
maкор 2m( пер vотн )
Проекция кориолисовой силы инерции на касательную к
относительной траектории точки всегда равна нулю
dvотн
и
m
Fi Fпер
dt
61.
Работа кориолисовой силы инерции на любомотносительном перемещении равна нулю
и теорема об изменении кинетической энергии
в относительном движении
будет иметь вид:
m
2
отн1
v
2
m
2
отн 0
v
2
Ai A( F )
и
пер






















































 Физика
Физика








