Динамика. Законы динамики

1. 1. Динамика.

• Динамика устанавливает и изучает связь между
движением материальных тел и действующими
на них cилами.
• В основе классической динамики лежат законы.

2. 2. Динамика.

• Первый закон (з-н инерции). Если на материальную точку не
действуют никакие силы, то эта точка или находится в покое,
или движется прямолинейно и равномерно.
Если F =0, то v =const.
В частности v =0.
• Свойство м. т. сохранять свою скорость неизменной как по
модулю, так и по направлению, в частности - состояние покоя,
называется инертностью или инерцией.
• Мерой ее является масса тела.
• Массой называют количества вещества в объеме тела.
Единица измерения массы – кг.

3. 3. Динамика.

• Второй закон (з-н зависимости между силой и количеством
движения) – основной закон динамики.
• Модуль силы, действующей на материальную точку, равен
произведению массы точки на модуль ее ускорения, а
направление силы совпадает с направлением ускорения.
ma F
• Векторное уравнение: F m. a
• При действии на точку нескольких сил:
ma R или ma
Fk .

4. 4. Динамика.

• Третий закон (з-н равенства действия и противодействия).
• Силы взаимодействия двух тел равны по величине и
направлены по одной прямой в противоположные стороны.

5. 5. Динамика.

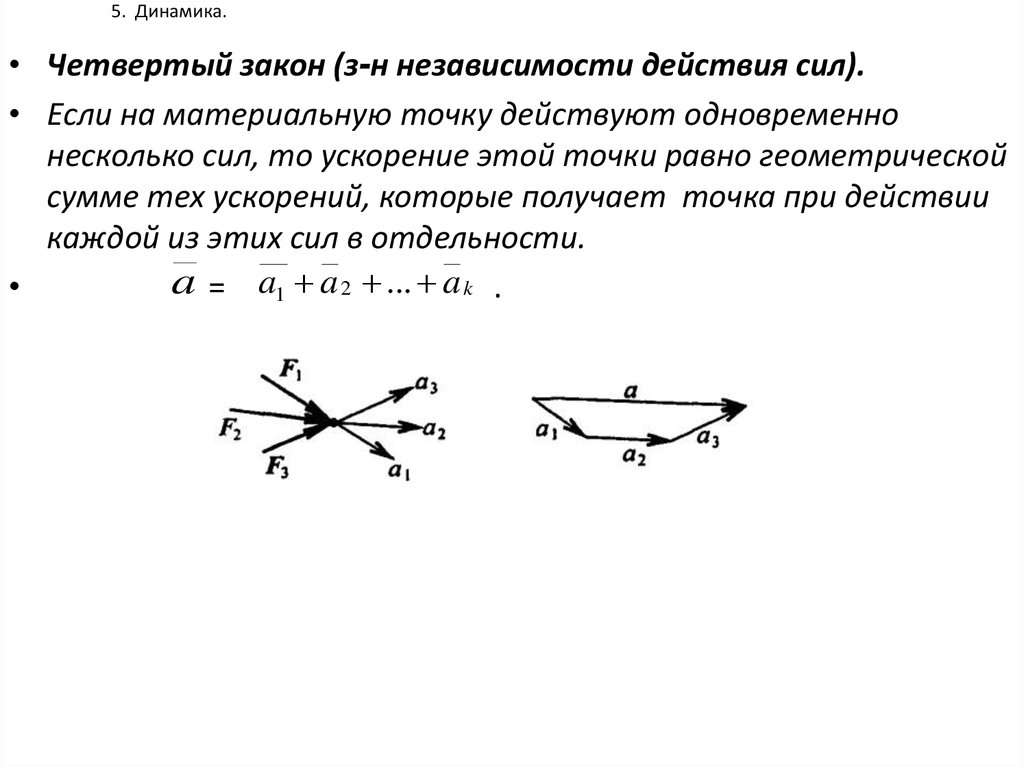
• Четвертый закон (з-н независимости действия сил).
• Если на материальную точку действуют одновременно
несколько сил, то ускорение этой точки равно геометрической
сумме тех ускорений, которые получает точка при действии
каждой из этих сил в отдельности.
a = a1 a 2 ... a k .

6. 6. Динамика.

• Системы единиц.
• Система СИ. Основные ед. изм. - длина, время и
масса (м, с, кг), сила измеряется производной
единицей – 1 ньютон (Н).
• 1 Н – это сила, сообщающая массе в 1 кг ускорение
1 м/с2 (1Н=1 кгм/с2).

7. 7. Динамика.

• Дифференциальные уравнения движения материальной
точки
Из основного закона : ma F k. . Проецируем обе части
2
d
равенства на оси x, y, z, учитывая, что a x x и т.д.
dt 2
d 2x
m 2 Fkx
dt
,
d2y
m 2 Fky
dt
,
d 2z
m 2 Fkz
dt
-
второй закон динамики в координатной форме.

8. 8. Динамика.

• Основные задачи динамики состоят в следующем:
– зная движение материальной точки или системы точек, найти
силы, действующие на эту точку или систему;
– зная силы, действующие на данную материальную точку или
систему, найти закон движения этой точки или системы
(основная задача динамики).
• Для несвободной материальной точки первая задача динамики
состоит в том, чтобы, зная движение точки и действующие
активные силы, найти реакцию связи. Вторая задача распадается
на две и состоит в том, чтобы, зная действующие силы,
определить: а) закон движения точки, б) реакцию наложенной
связи.

9. 9. Динамика.

• Первая задача динамики (определение сил по заданному
движению).
• 1. Если задано ускорение точки a , то действующая сила или
реакция находится из уравнений:
(второй закон).
F ma и F ma
• 2. Если известен закон движения точки, а ускорение не задано,
то силы определяются из уравнений:
d 2z
d 2x
d2y
,
,
.
(1)
m
F
m
F
m
F
dt 2
kx
dt 2
ky
dt 2
kz
Определив три проекции искомой силы, мы будем знать ее модуль и направление в
каждый момент времени.

10. 10. Динамика.

• Вторая задача динамики (основная).
• Известна сила. Найти закон движение точки, т.е. выразить ее координаты как
функции времени.
• Решение сводится к интегрированию уравнений (1).
m
d 2x
Fkx
dt 2
m
d2y
Fky
dt 2
m
d 2z
Fkz
dt 2
• Пример. Прямолинейное движение точки. Найдем закон движения
x f (t )
.
• Движение точки
определяется уравнением:
2
d x
m 2 Fkx ,
или m d v x F.
(2)
dt
kx
dt
• Интегрируем (2).
• Решение : x=f(t, C1 , C2 ).
• Для определения постоянных C1 и C2 вводят начальные условия. Закон
движения точки запишется в виде: x f (t , x0 , v0 ) .
• Если требуется найти зависимость v f (x) , то уравнение (2)
d vx
dv dx
dv
преобразовывают:
m
m x
mvx x Fkx
dt dx
dx
dt
.

11. 11. Динамика.

• Механической системой материальных точек (системой) в
механике называется совокупность конечного или бесконечного числа
материальных точек, связанных между собой так, что движение
каждой точки не является независимым от движения остальных точек.
a
k
• Активные силы F и реакции связей N k разделяют на внешние
e
F
k , действующие со стороны посторонних тел, не входящие в
систему, и внутренние F ik , с которыми составляющие данной
системы действуют друг на друга.
• Свойства внутренних сил:
• 1. Геометрическая сумма (главный вектор) всех внутренних сил
системы равняется нулю.
i
F
• Свойство объясняет третий закон динамики. k =0.
• 2. Сумма моментов (главный момент) всех внутренних сил системы
относительно любого центра или оси равняется нулю.
m0 (F k ) 0
i
Рис.69.

12. 12. Динамика.

• Дифференциальные уравнения движения системы.
• Для точки основной закон динамики:
e
i ;
mk a k F k F k
e
F
k - равнодействующая внешних сил (активных и реакций связей);
F k - равнодействующая внутренних сил.
Для системы:
i
e
i
m1 a1 F 1 F 1 ,
e
i
m2 a 2 F 2 F 2 ,
............
e
i
mn a n F n F n • дифференциальные уравнения движения системы в векторной
форме ( a k v k r ).
k

13. 13. Динамика.

• Масса системы М (m) равна арифметической сумме масс всех
точек или тел, образующих систему:
M mk .
• Распределение масс в системе определяется значениями масс
точек m k и их координатами x k , y k , z k .
• Центр масс и центр тяжести тела.
• Центром тяжести твердого тела С называется неизменно
связанная с этим телом точка, через которую проходит линия
действия равнодействующей сил тяжести, действующих на
частицы данного тела, при любом положении тела в
pk .
пространстве. P
• Координаты центра тяжести тела:
1
xC p k x k
P
1
, yC p k y k
P
1
, zC pk z k .
P

14. 14. Динамика. Центр масс.

• Центр масс тела совпадает с положением его центра
тяжести.
• Учтем, что pk mk g и P Mg :
1
,
,
(1)
1
1
xC
mk x k ,
yC
M
m
M
k
yk
zC
m
M
k
zk
• где m k , x k , y k , z k - масса и координаты точек системы.
• Геометрическая точка тела С, координаты которой
определяются формулами (1), называется центром масс или
центром инерции механической системы.
• Из равенства (1) - положение ЦМ определяем через радиус• вектор
.
1
rC
m
M
k
rk
r k - радиусы-векторы точек системы.

15. 15. Динамика.

• Момент инерции тела относительно оси.
• Моментом инерции тела (системы) относительно данной оси
Oz называется скалярная величина, равная сумме произведений
масс всех точек тела (системы) на квадраты их расстояний
от этой оси:
2
J
m
h
k
k k .
• Единица измерения в системе СИ – 1 кг м 2 .
• Радиусом инерции тела относительно оси Oz называется
линейная величина z , определяемая равенством:
.
J z M z2
M – масса тела. Из равенства следует, что радиус инерции равен расстоянию
от оси Oz такой точки, в которой нужно сосредоточить всю массу тела, чтобы
момент инерции этой сосредоточенной массы был равен моменту инерции
тела относительно данной оси.

16.

17.

18. Движение материальной точки. Метод кинетостатики.

19. 19. Движение материальной точки. Метод кинетостатики.

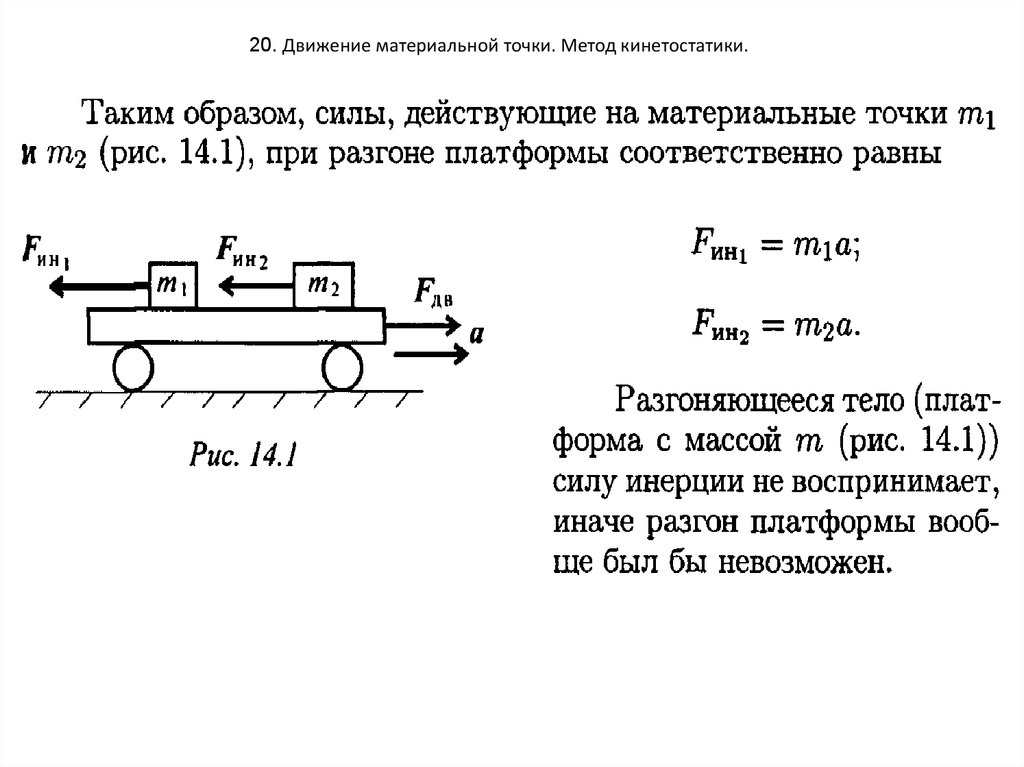
20. 20. Движение материальной точки. Метод кинетостатики.

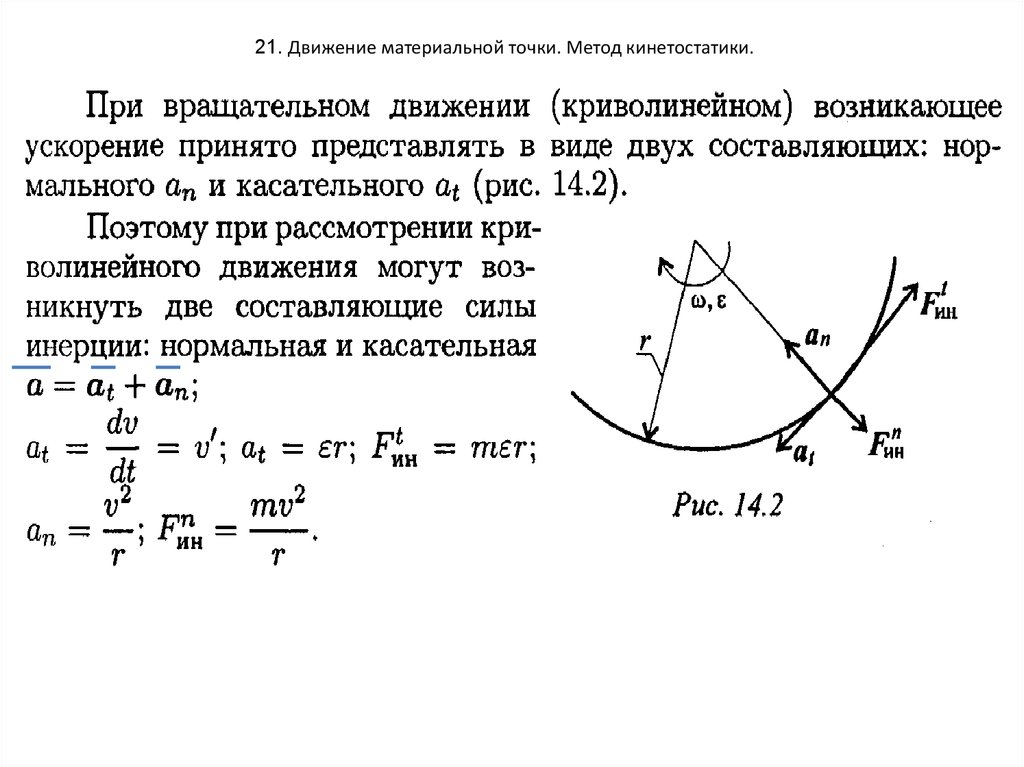
21. 21. Движение материальной точки. Метод кинетостатики.

22. 22. Движение материальной точки. Метод кинетостатики.

23. 23. Движение материальной точки. Метод кинетостатики.

24. 24. Динамика.

• Работа силы, действующей на точку.
• Работа силы характеризует те действия, которые сила оказывает
на тело при его перемещении, и меру действия силы, которая
приводит к изменению модуля скорости точки.
• Элементарной работой dA силы F , приложенной в точке М,
называется величина
dA F ds ,
(1)
• где F - проекция силы F на касательную M к траектории
точки М, направленную в сторону перемещения точки
(направление скорости v ); ds - элем-е перем-е точки М.

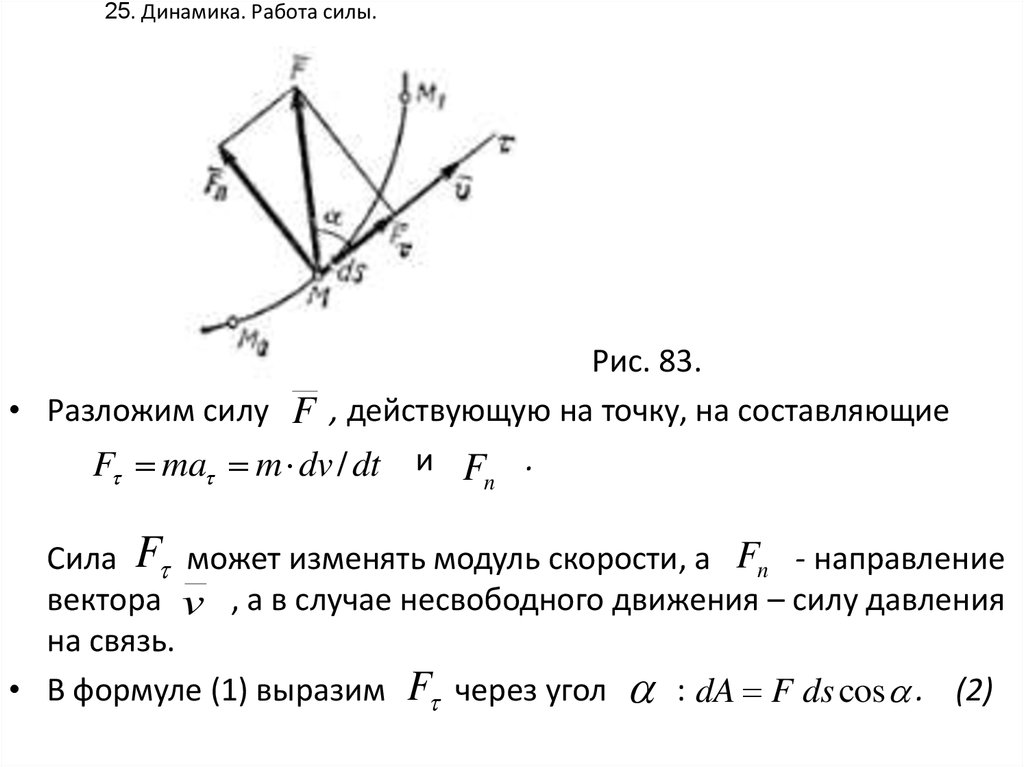
25. 25. Динамика. Работа силы.

Рис. 83.
• Разложим силу F , действующую на точку, на составляющие
F ma m dv / dt и F .
n
Сила F может изменять модуль скорости, а Fn - направление
вектора v , а в случае несвободного движения – силу давления
на связь.
• В формуле (1) выразим F через угол : dA F ds cos . (2)

26. 26. Динамика. Работа силы.

• Работа dA 0, если угол - острый, сила ускоряет движение
точки и направлена в сторону движения; dA 0, если угол тупой, и сила замедляет движение. При =0 dA F ds ,
при 180 0
dA F ds .
• Если угол 90 0 - сила направлена перпендикулярно
перемещению, и dA=0.
• Определим работу силы на конечном перемещении M o M 1 .
Проинтегрируем (1):
( M1 )
.
A( M o M1 )
F ds
(Mo )
• След-но, работа силы на любом перемещении M o M 1 равна
взятому вдоль этого перемещения интегралу от
элементарной работы.
При F =const и M o M 1 = s1 получаем A( M o M 1 ) F s1

27. 27. Динамика. Работа силы.

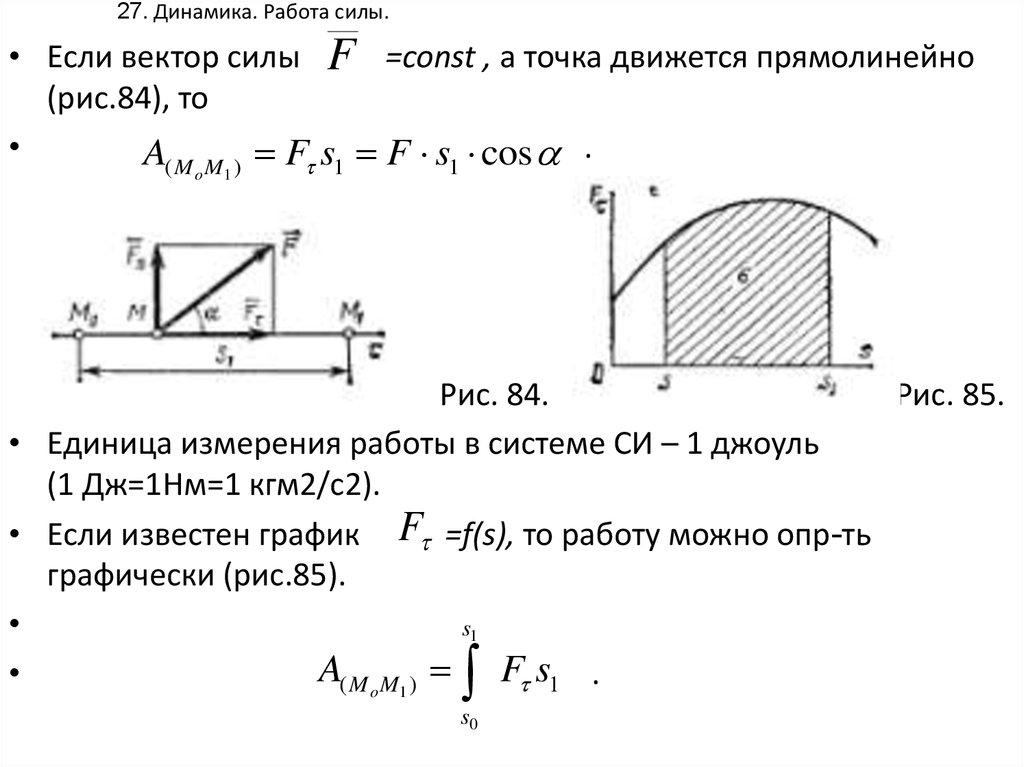
• Если вектор силы F =const , а точка движется прямолинейно
(рис.84), то
A( M M ) F s1 F s1 cos .
o
1
Рис. 84.
Рис. 85.
• Единица измерения работы в системе СИ – 1 джоуль
(1 Дж=1Нм=1 кгм2/с2).
• Если известен график F =f(s), то работу можно опр-ть
графически (рис.85).
s1
A( M oM1 ) F s1 .
s0

28. 28. Динамика.

• Мощностью называется величина, определяющая работу,
совершаемую силой в единицу времени:
N dA / dt F ds / dt F v
.
• След-но, мощность равна произведению касательной
составляющей силы на скорость.
• Если работа совершается равномерно, то мощность N A / t1 ,
где t1 - время, в течении которого совершается работа А.
• Единица измерения мощности в системе СИ – ватт (1 Вт=1дж/с).
• В технике - работа измеряется в киловатт-часах
(1 кВтч=3,6х 10 6 Дж 367100 кГм), а за единицу мощности
часто принимается 1 л.с. = 736 Вт.

29. 29. Динамика.

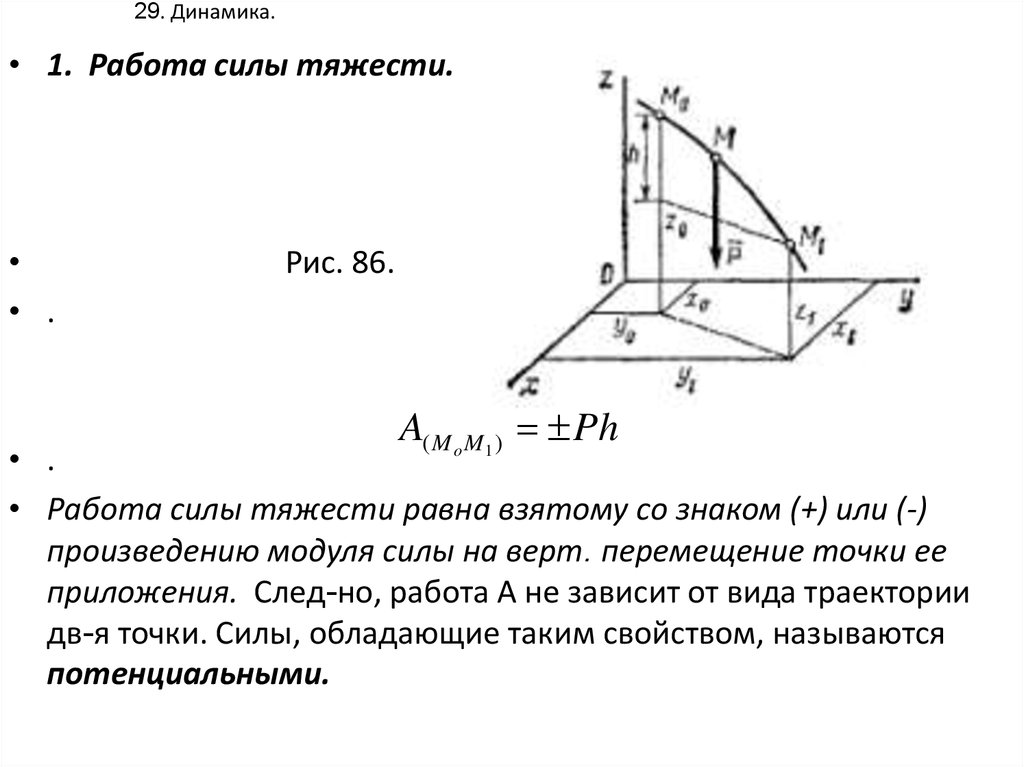
• 1. Работа силы тяжести.
• .
Рис. 86.
A( M o M1 ) Ph
• .
• Работа силы тяжести равна взятому со знаком (+) или (-)
произведению модуля силы на верт. перемещение точки ее
приложения. След-но, работа А не зависит от вида траектории
дв-я точки. Силы, обладающие таким свойством, называются
потенциальными.

30. 30. Динамика.

• 3. Работа силы трения.
Рис. 87А.
• Направление F тр противоположно перемещению точки.
Следовательно , работа силы на конечном перемещении
(M )
M
M
.
A( M o M1 )
1
F
тр
(Mo )
1
1
M0
M0
ds Fтр ds fNds
• Если сила трения по модулю постоянна, то A( M 0 M1 ) Fтр s .
Здесь s – длина дуги кривой M O M 1 .
• 1. Работа силы трения всегда отрицательна.
• 2. Работа силы трения зависит от длины дуги M O M 1 , поэтому
является силой непотенциальной.

31. 31. Динамика.

• Вычисление работы сил, действующих на систему.
• 1. Работа сил тяжести, действующих на систему.
A PhC
,
• где Р – вес системы, hC - вертикальное перемещение ЦМ или
ЦТ .

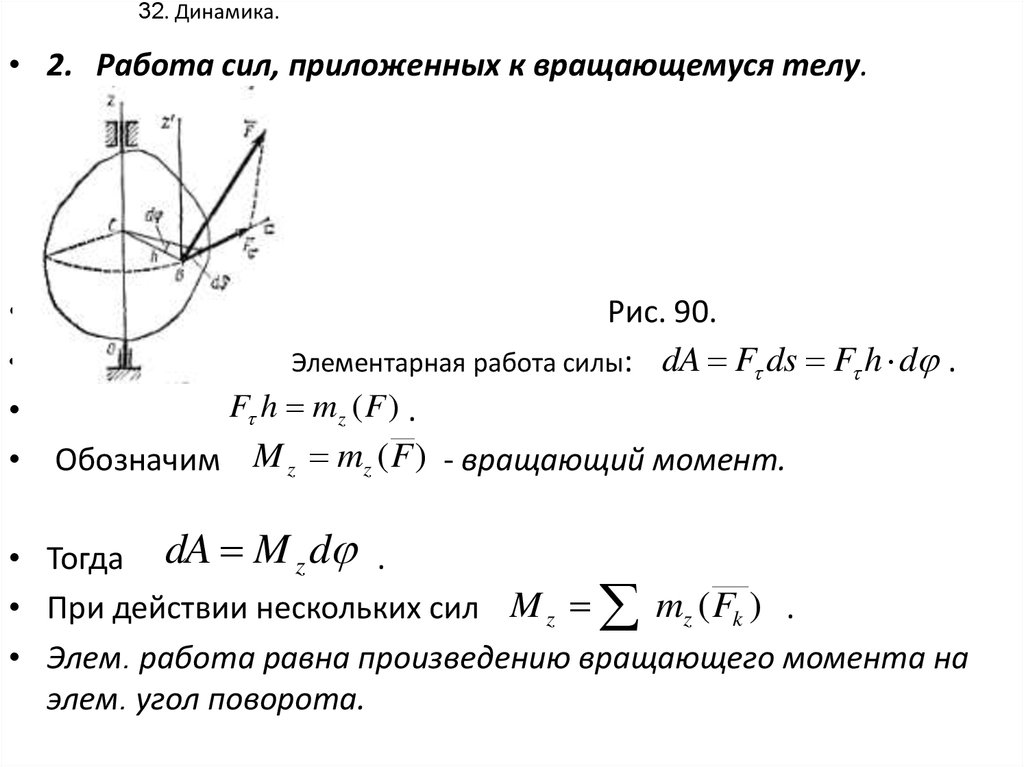
32. 32. Динамика.

• 2. Работа сил, приложенных к вращающемуся телу.
Рис. 90.
Элементарная работа силы: dA F ds F h d .
F h mz (F ) .
Обозначим M z mz (F ) - вращающий момент.
• Тогда dA M z d .
mz ( Fk ) .
• При действии нескольких сил M z
• Элем. работа равна произведению вращающего момента на
элем. угол поворота.

33. 33. Динамика. Работа сил, приложенных к вращающемуся телу.

1
• При повороте на конечный угол 1 работа равна A M z d .
0
• В случае постоянного момента : A M z 1 .
• Если на тело действует пара сил, лежащая в плоскости,
перпендикулярной оси Оz, то в формулах момент M z будет
моментом пары.
• Мощность.
.
N dA / dt M z d / dt M z
• При действии сил на вращающееся тело мощность равна
произведению вращающего момента на угловую скорость
тела.

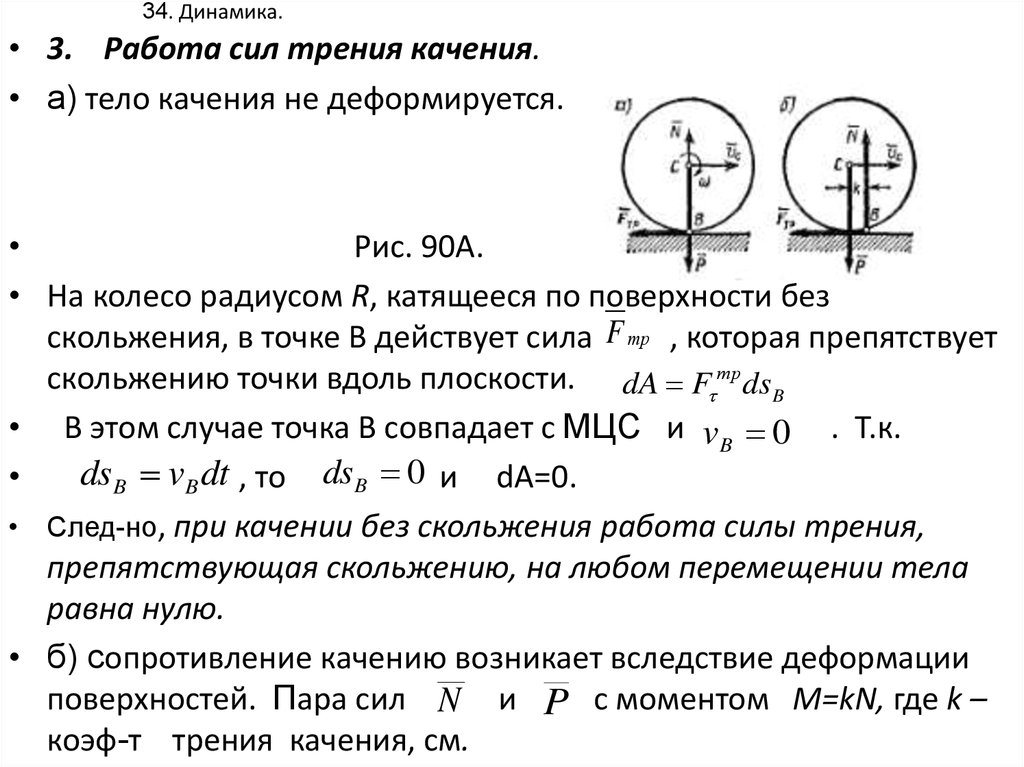
34. 34. Динамика.

• 3. Работа сил трения качения.
• а) тело качения не деформируется.
Рис. 90А.
• На колесо радиусом R, катящееся по поверхности без
скольжения, в точке В действует сила F тр , которая препятствует
скольжению точки вдоль плоскости. dA F тр dsB
• В этом случае точка В совпадает с МЦС и vB 0 . Т.к.
ds B vB dt , то dsB 0 и dA=0.
• След-но, при качении без скольжения работа силы трения,
препятствующая скольжению, на любом перемещении тела
равна нулю.
• б) сопротивление качению возникает вследствие деформации
поверхностей. Пара сил N и P с моментом M=kN, где k –
коэф-т трения качения, см.

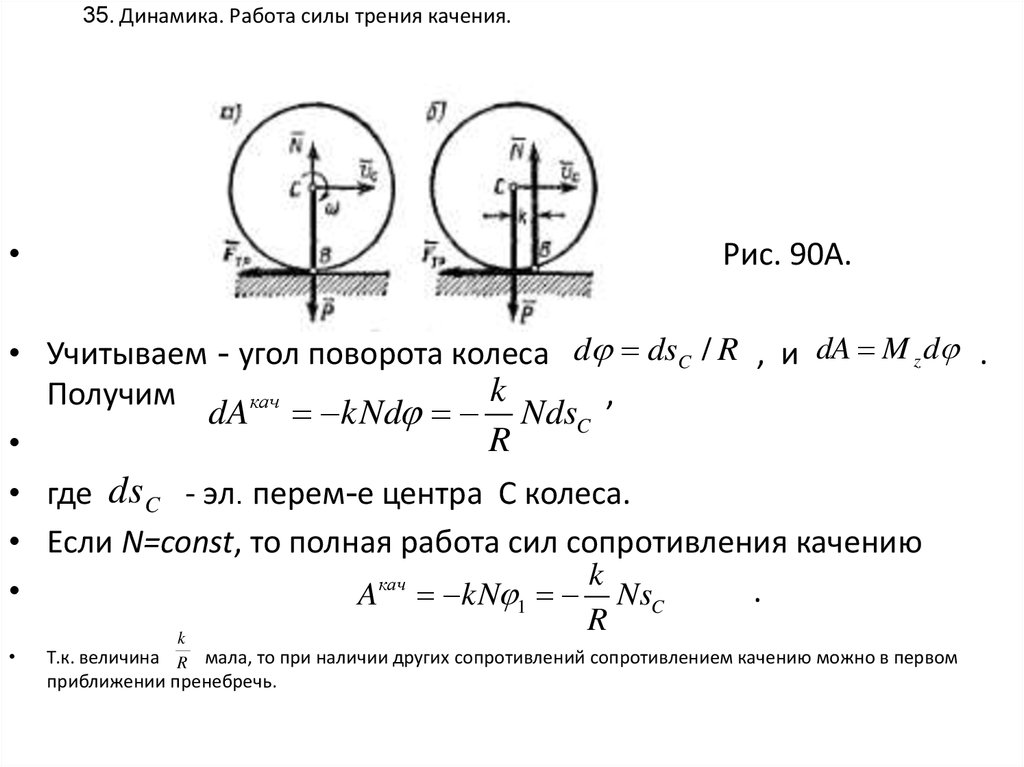
35. 35. Динамика. Работа силы трения качения.

Рис. 90А.
• Учитываем - угол поворота колеса d dsC / R , и dA M z d .
k
Получим
,
кач
dA kNd NdsC
R
• где ds C - эл. перем-е центра С колеса.
• Если N=const, то полная работа сил сопротивления качению
k
кач
.
A kN 1 NsC
R
k
Т.к. величина R мала, то при наличии других сопротивлений сопротивлением качению можно в первом
приближении пренебречь.

36. 36. Работа и мощность. Коэффициент полезного действия.

37. 37. Динамика.

• Количество движения материальной точки.
• Количеством движения м.т. называется векторная величина,
равная произведению массы точки на ее скорость mv .
• Кол-во дв-я совпадает по направлению со скоростью точки.
• Ед. изм. в системе СИ – 1 кгм/с=1Нс.
• Элементарный импульс силы – векторная величина d S , равная
произведению силы F на элементарный промежуток
времени dt: d S F dt .
• Вектор d S
направлен вдоль линии действия силы.
• Импульс силы S за некоторый промежуток времени t1 равен
определенному интегралу от элементарного импульса, взятому в
t1
пределах от нуля до t1 .
СИ – 1 кгм/с
S F dt
.
0
• Если сила F = const, то S Ft1 , модуль S Ft1 .
t1
• Проекции на координатные оси:
S x Fx dt
и т.д.
0

38. 38. Динамика.

• Теорема об изменении количества движения точки.
• Основной закон динамики : ma F k . Ускорение a d v /dt .
• Тогда:
d (mv)
Fk
,
dt
• т.е. производная по времени от количества движения точки равна
сумме действующих на точку сил.
• Проинтегрируем в пределах: время от 0 до t1 и скорость от v 0 до v 1 :
t1
mv 1 mv 0 Fk dt
mv1 mv 0 S k
- импульсы действ. сил.
0
.
• Изменение количества движения точки за некоторый промежуток
времени равно сумме импульсов всех действующих на точку сил за
тот же промежуток времени.
• При решении задач – ур-я в проекциях:
mv1x mv0 x S kx и т.д. .

39. 39. Динамика.

• Количество движения системы.
• Количество движение системы – это векторная величина , равная
геометрической сумме (главному вектору) количеств движения всех
точек системы: Q
.
m v .
k
k
Рис.74
• Радиус-вектор центра масс системы равен: r C 1
mk r k ,
M
или mk r k M rC .
• Производная по времени частей уравнения:
d rk
d rC , или
mk v k M vC , или Q M vC .
m
M
k
dt
dt
• Количество движения системы равно произведению массы системы
на скорость ее ЦМ.
Количество движения характеризует только поступательную часть
движения системы. Напр., если при движении тела системы ЦМ
остается постоянным (вращательное движение), то Q =0 .

40. 40. Динамика.

• Теорема об изменении количества движения системы.
• Система состоит из n м. т. Сложим почленно уравнения
основного закона динамики точек системы:
e
i
m
a
F
F
k k k k .
d
dQ .
• Здесь F ik 0 , а
m ak
m v
k
dQ
dt
k
k
dt
• Тогда, окончательно
(7)
Fk dt
• - теорема в дифференциальной форме:
• Производная по времени от количества движения системы
равна геометрической сумме всех действующих на систему
внешних сил.
• Проектируем на координ. оси:
dQx
e
и т.д.
F
dt
kx
e

41. 41. Динамика. Теорема об изменении количества движения системы.

• Найдем выражение теоремы в интегральной форме.
• Проинтегрируем выражение (7) в соотв. интервалах, умножая обе
части равенства на dt:
t
t
e
e
Q1 Q 0 Fke dt . Поскольку S k Fk dt - импульс
1
0
0
Q1 Q 0 S k .
• внешних сил, получим
• Изменение количества движения системы за некоторый
промежуток времени равно сумме импульсов действующих на
систему внешних сил за тот же промежуток времени.
• В проекциях на координатные оси:
и т.д.
Q x1 Q 0 x S kxe
e
• Практическая ценность теоремы заключается в том, что позволяет при
решении задач исключить неизвестные внутренние силы, действующие на
систему.

42. 42. Динамика.

Следствия теоремы :
e
F
1. Если k =0,
dQ
e
F
0 , Q const
тогда
.
k
dt
Если сумма всех внешних сил, действующих на систему, равна
нулю, то вектор количества движения системы постоянен по
модулю и направлению.
• 2. Если F kx 0 , тогда Qx const .
• Если сумма проекций всех действующих внешних сил на какуюнибудь ось равна нулю, то проекция количества движения
системы на эту ось есть величина постоянная.
• Вывод: на количество движения системы внутренние силы,
действующие на систему, не могут повлиять; и это есть закон
сохранения количества движения.
e

43. 43. Динамика.

• Теорема о движении центра масс системы.
Для определения характера движения системы часто требуется знание закона движения ее ЦМ.
• Дифф. ур-я дв-я системы в векторной форме сложим почленно:
mk a k F k F. k (7)
1
mk r k M r C
Радиус-вектор ЦМ: r C mk r k , отсюда
M
.
Производные по времени от обеих частей равенства:
d 2 rk
d 2 rC или
m
M
mk a k M a C .
e
i
• Т.к.
k
F
dt 2
i
k
dt 2
0 , получим окончательно
M aC F k
e
.
(8)
Произведение массы системы на ускорение ее ЦМ равно
геометрической сумме всех действующих на систему внешних сил.

44. 44. Динамика. Теорема о движении центра масс системы.

Вывод: ЦМ системы движется как МТ, масса которой равна массе
всей системы и к которой приложены все внешние силы,
действующие на систему.
• Дифференциальные уравнения движения ЦМ в проекциях на
координатные оси:
e
и т.д.
M x C F kx
• Практическое значение:
• 1. Если рассматривается движение тела как движение МТ, то з-н его
движения принимается соответствующим з-ну движения ЦМ.
• 2. Теорема позволяет исключать из рассмотрения неизвестные
внутренние силы при определении з-на движения ЦМ системы.

45. 45. Динамика.

• Кинетическая энергия точки.
• Кинетической энергией МТ называется скалярная величина
mv 2 / 2
, равная половине произведения массы точки на
квадрат ее скорости.
• Единица измерения в системе СИ – 1 Дж.
• Найдем взаимосвязь работы и кинетической энергии.
• Точка М с массой m перемещается из точки M O ( v0 ) в точку
• M 1 ( v1 ).
• Основной з-н динамики: ma F k . Проецируем на
касательную , направленную в сторону движения:
dv dv ds
dv .
ma F k .
a
v
dt ds dt
ds
dv
mv (ds ) F k (ds ) .
ds
Fk ds dAk - эл. работа силы F k .

46. 46. Динамика. Кинетическая энергия точки.

• Окончательно:
mv 2
dAk
d
2
- выражение
• теоремы об изменении кинетической энергии точки в
дифференциальной форме.
• Проинтегрируем :
mv12 mv02
A( M 0 M1 )
.
(5)
2
2
• Ур-е (5) выражает теорему об изменении кинетической
энергии точки:
• Изменение кинетической энергии точки при некотором ее
перемещении равно алгебраической сумме работ всех
действующих на точку сил на том же перемещении.
• В случае несвободного движения точки в правую часть равенства
войдет работа активных сил и работа реакций связи.

47. 47. Динамика.

• Кинетическая энергия системы.
• Кинетической энергией системы называется скалярная
величина Т, равная сумме кинетических энергий всех точек
системы:
2
T
m
v
k k /2 .
• 1. Поступательное движение.
При поступательном движении все точки тела движутся с одинаковыми скоростями, в том числе и ЦМ.
Tпост m v / 2 ( mk )v / 2 Mv / 2
2
k С
2
C
2
C
.
• Т.обр., кинетическая энергия тела при поступательном
движении равна половине произведения массы тела на
квадрат скорости ЦМ.

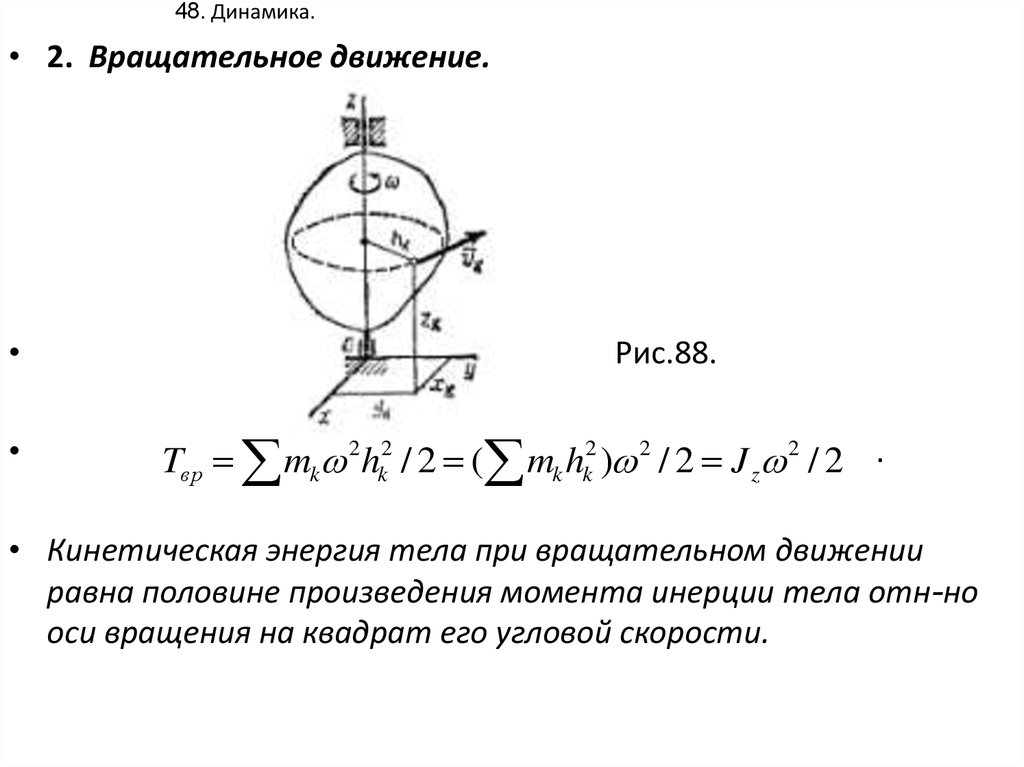
48. 48. Динамика.

• 2. Вращательное движение.
Рис.88.
Tвр mk 2hk2 / 2 ( mk hk2 ) 2 / 2 J z 2 / 2 .
• Кинетическая энергия тела при вращательном движении
равна половине произведения момента инерции тела отн-но
оси вращения на квадрат его угловой скорости.

49. 49. Динамика.

• 3. Плоскопараллельное движение.
Все точки тела совершают движение в плоскости, параллельной неподвижной плоскости. Это движение можно
представить как вращение вокруг оси, перпендикулярной неподвижной плоскости и проходящей через
мгновенный центр скоростей Р. При этом необходимо помнить, что мгновенный центр скоростей все время
меняет положение.
• т. Р – МЦС.
Рис.89.
Tпл оск J P 2 / 2
,
• где J - момент инерции тела отн-но оси Р .
P
Tплоск MvC2 / 2 J С 2 / 2
• При плоскопараллельном движении кинетическая энергия тела
равна энергии поступ. движения со скоростью ЦМ, сложенной
с кинетической энергией вращ. движения вокруг ЦМ.

50. 50. Динамика.

• Теорема об изменении кинетической энергии системы.
• Рассмотрим систему, состоящую из n мат. точек.
• Для каждой точки с массой m k и скоростью vk справедливо
2
равенство:
d (mk vk / 2) dAke dAki
,
e
i
dA
,
dA
• где
k
k - элем. работы внешних и внутренних сил,
действующих на точку.
• Урав-я для всех точек сложим почленно:
2
e
i ,
d ( mk vk / 2) dAk dAk
или
dT dAke dAki
.
(1)
• Равенство выражает теорему в дифференциальной форме.

51. 51. Динамика. Теорема об изменении кинетической энергии системы.

• Проинтегрируем обе части равенства в пределах, соответствующих
перемещению системы из начального положения ( Т= T0 ) в положение,
где Т = T1 :
T1 T0 A A
e
k
i
k
-
(2)
• - теорему в интегральной форме:
• Изменение кинетической энергии системы при некотором ее
перемещении равно сумме работ на этом перемещении всех
приложенных к системе внешних и внутренних сил.
Рис. 91.
В точках B1 и B2 силы взаимодействия направлены по линии действия, однако точки могут
перемещаться навстречу друг другу, поэтому работа каждой из сил будет положительной и сумма
их не будет равна нулю.

52. 52. Динамика.

1. Основное уравнение динамики при поступательном движении
твердого тела.
• Дв-е сводится к задачам динамики точки, т.к. такое дв-е тела
всегда можно рассматривать как дв-е МТ с массой, равной массе
тела (результат теоремы о движении ЦМ). Дифф-е уравнения
движения ЦМ:
e
M
x
F
kx ,
C
M y C F ky ,
M z C F kz
e
e
.

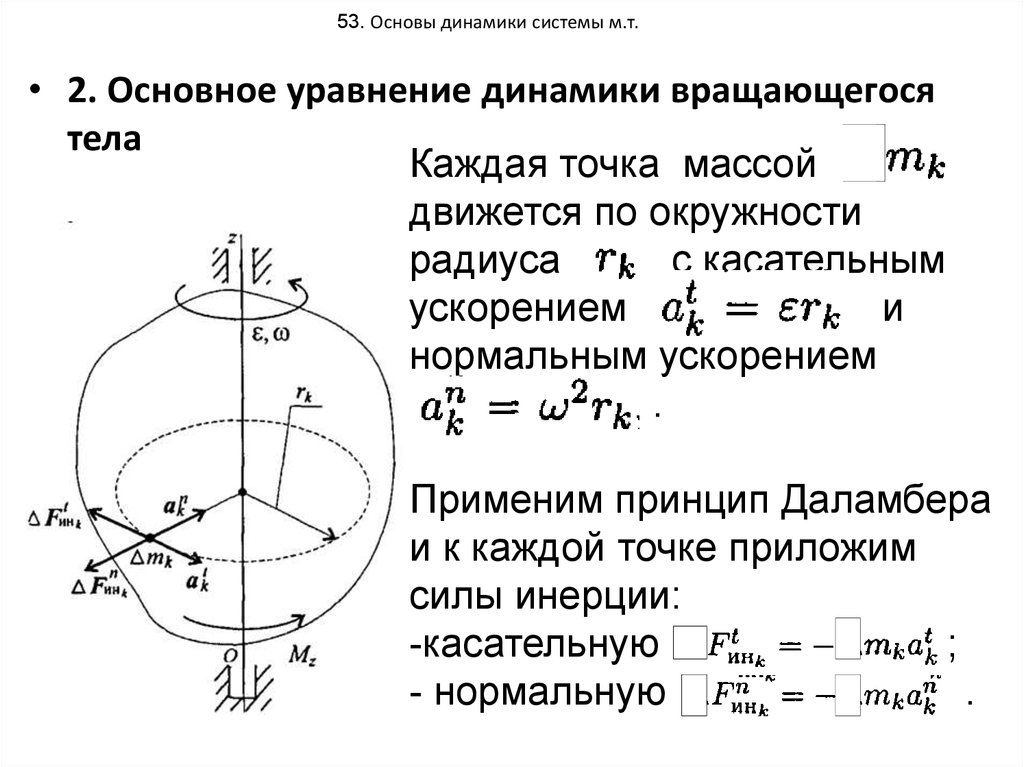
53. 53. Основы динамики системы м.т.

• 2. Основное уравнение динамики вращающегося
тела
Каждая точка массой
движется по окружности
радиуса
с касательным
ускорением
и
нормальным ускорением
.
Применим принцип Даламбера
и к каждой точке приложим
силы инерции:
-касательную
;
- нормальную
.

54. 54. Основы динамики системы м.т.

• Система сил, действующая на точку, находится в
равновесии, поэтому
момент внешних
сил.
Моменты нормальных сил инерции
равны нулю. Силы, направленные по касательной:
- подставим в ф-лу.

55. 55. Основы динамики системы м.т.

• Получим выражение основного уравнения
динамики вращающегося тела:
• Момент инерции тела в этом выражении определяет
меру инертности тела при вращении.
• В системе СИ