Похожие презентации:
Перспектива. Построение изображения пространственных форм на плоскости
1. 2 семестр
• Дисциплина: «Начертательная геометрия»Цель изучения дисциплины во 2 семестре:
Формирование у студента системы
теоретических знаний об основных способах
построения изображения пространственных
форм на плоскости (метод центрального
проецирования).
Развитие пространственного воображения,
творческого мышления
2.
Задачи:• освоение способов изображения различных форм,
поверхностей, архитектурных деталей в перспективных
проекциях
•
изучение теории теней и использование полученных
знаний для выявления объема на плоскости. Овладение
основами построения теней в
перспективных
проекциях (солнечные и факельные тени);
• овладение различными способами построения
перспективных проекций для максимально объективного
изображения заданного или спроектированного объекта.
• формирование профессиональных качеств, практических
навыков и умений по созданию и чтению различных чертежей,
знакомство с приемами и правилами их выполнения и
оформления;
• развитие графических навыков работы с различными
чертежными инструментами
• освоение способов изображения различных объектов при
вертикальной планировке территории.
3. Модуль 3. Перспектива
Темы модуля:• Основные положения. Перспектива точки, прямой,
плоскости.
• Способы построения перспективы: способ
архитекторов с двумя точками схода, с недоступной
точкой схода, с применением опущенного (поднятого)
плана и боковой стены, способ прямоугольных
координат и перспективной сетки.
• Построение теней в перспективе.
• Построение фронтальной и угловой перспективы
интерьера. Тени в интерьере.
• Построение
отражений в зеркальной
плоскости.
• Реконструкция перспективного
изображения
и
приемы фотомонтажа в
перспективе.
4. Модуль 4. Проекции с числовыми отметками
Темы модуля:• Общие сведения. Сущность способа. Применение
метода проекций с числовыми отметками в
архитектурном проектировании. Понятия и
определения. Точка, прямая, плоскость.
• Понятие «интервала» и «уклона» прямой и
плоскости. Взаимное расположение прямых.
Проекции плоскости. Взаимное положение точки,
прямой и плоскости. Пересечение плоскостей.
• Проекции поверхностей. Основы вертикальной
планировки.
5. Лекция 19
ПЕРСПЕКТИВА
Основные понятия и методы
Место и значение перспективы в
архитектурном проектировании
Геометрические основы перспективы
Перспектива точки, прямой
Дистанционные точки
6.
arch. HENRI CIRIANIПерспективой называется геометрическая модель, образованная
центральным проецированием фигуры-оригинала и
удовлетворяющая определенным условиям, учитывающим
особенности зрения.
7. Место и значение перспективы в архитектурном проектировании
• Ортогональные чертежи позволяютархитектору установить реальные
основы функционального,
конструктивного и художественного
решения. Но чтобы «прочесть» чертежи
объекта, необходимо за отдельными
проекциями увидеть проектируемое
сооружение во всей сложности его
объемно- пространственной структуры.
8.
С помощью перспективы можно получитьнаглядное изображение несуществующего,
проектируемого объекта.
Перспектива имеет некоторые преимущества по
сравнению с макетами зданий:
• макет позволяет видеть объемно-планировочную
структуру принятого композиционного решения,
но не позволяет отобразить внутреннее
пространство.
• Перспектива позволяет отразить особенности
восприятия объекта с конкретных точек зрения,
передает реальную освещенность, цвета,
материалы и воздушную перспективу.
Таким образом, перспектива приобретает большую
наглядность и выразительность
9.
Арх. Генри ЧирианиГоспиталь SAINTANTOINE
10. Назначение перспективы
• Перспектива позволяет на стадиипроектирования выявить недостатки
архитектурного решения и в процессе
разработки имеет важное
корректирующее значение
• Представляет наглядную иллюстрацию
и может показать достоинства уже
законченного проекта
11. Три основных этапа применения перспективы в творчестве архитектора
Начальная стадия- процессэскизирования –требует знания
законов перспективы и умения
свободно их использовать в рисунке.
Дает первое объемнопространственное выражение
композиции проектируемого объекта,
позволяет сопоставить и рассмотреть
различные варианты ее проработки
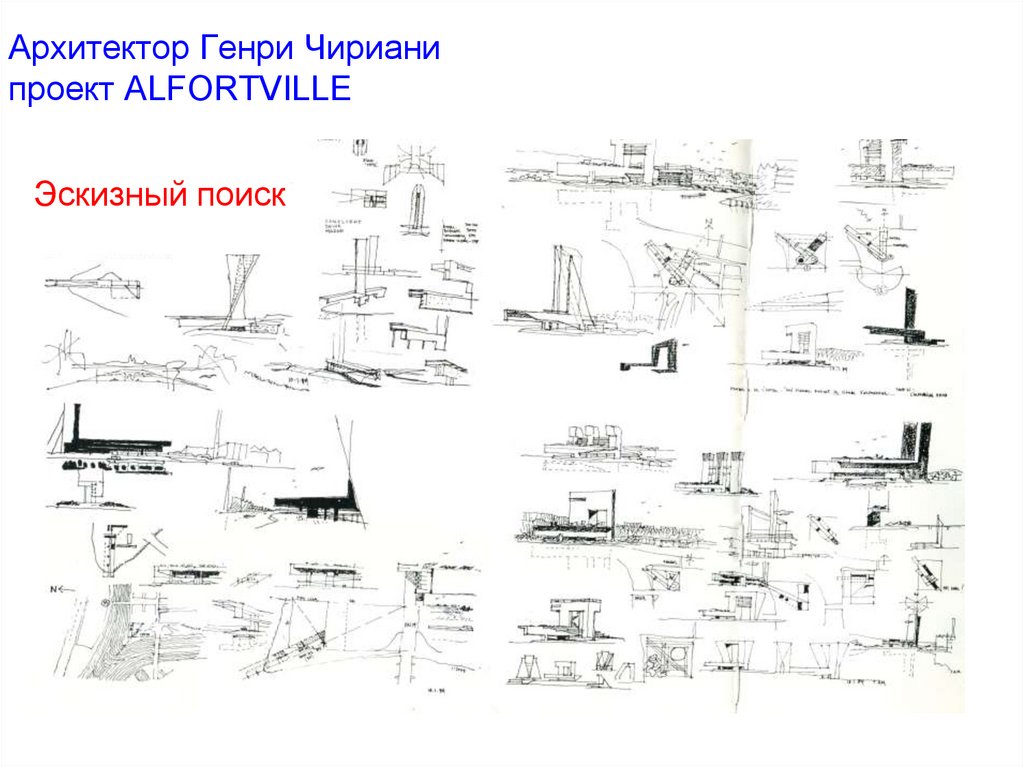
12. Архитектор Генри Чириани проект ALFORTVILLE
Эскизный поиск13.
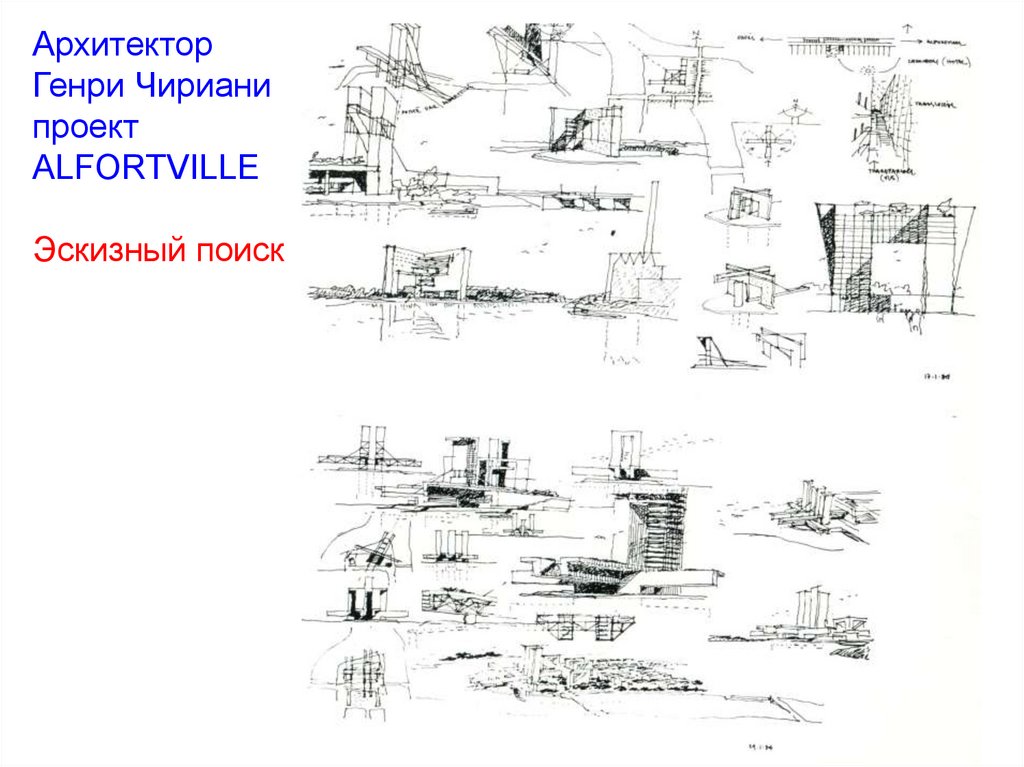
АрхитекторГенри Чириани
проект
ALFORTVILLE
Эскизный поиск
14. Три основных этапа применения перспективы в творчестве архитектора
Второй этап- окончательный выборконкретного архитектурного решения и
его закрепление в ортогональных
проекциях. Точное построение
перспективы. Служит для проверки
принятого композиционного решения,
а также для его уточнения,
дальнейшей проработки и внесения
необходимых коррективов в
ортогональные чертежи
15.
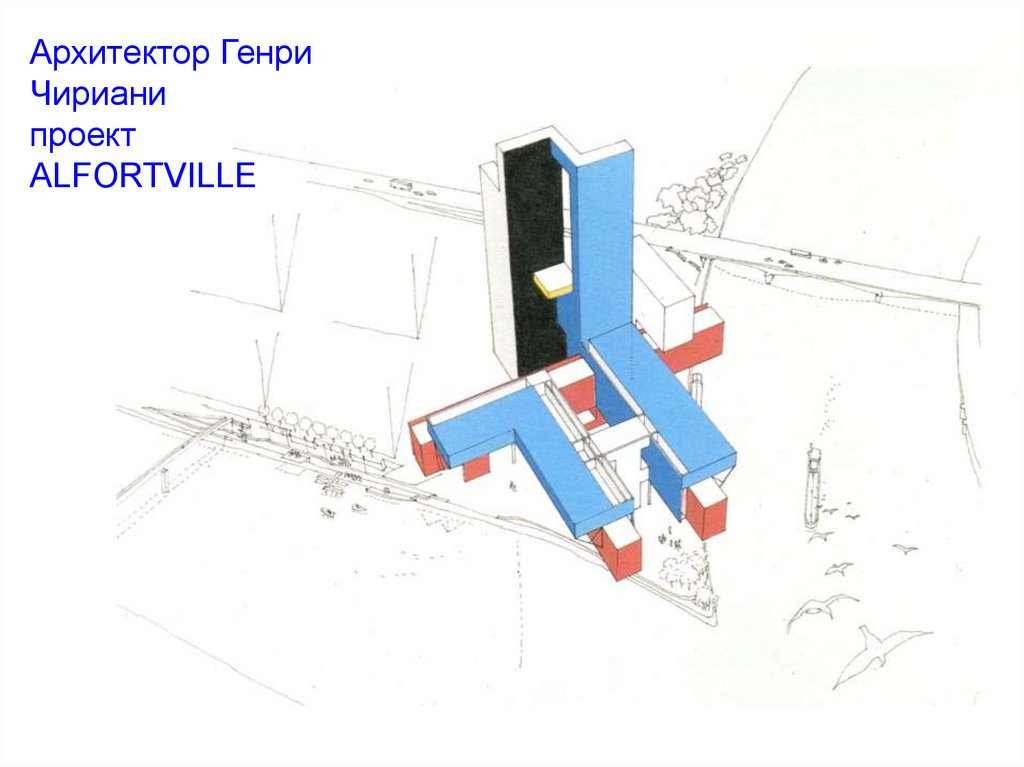
Архитектор ГенриЧириани
проект
ALFORTVILLE
16.
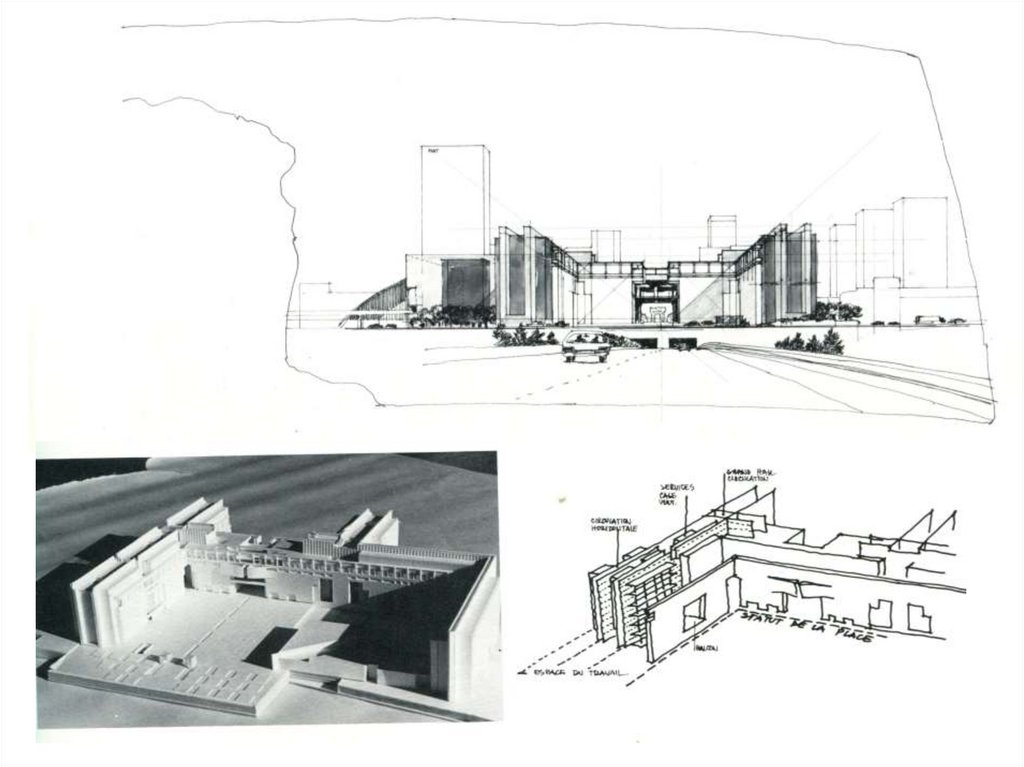
Архитектор ГенриЧириани
проект
ALFORTVILLE
17. Три основных этапа применения перспективы в творчестве архитектора
Третий этап- связан с завершениемпроработки композиции объекта с
окружающей средой.
Правильная передача всех деталей,
материалов, цвета и освещения
способствует наиболее полному
раскрытию общего композиционного
замысла
18.
Архитектор ГенриЧириани
проект
ALFORTVILLE
19.
АрхитекторГенри Чириани
Проект район Дефанс
(Париж, Франция)
20.
21.
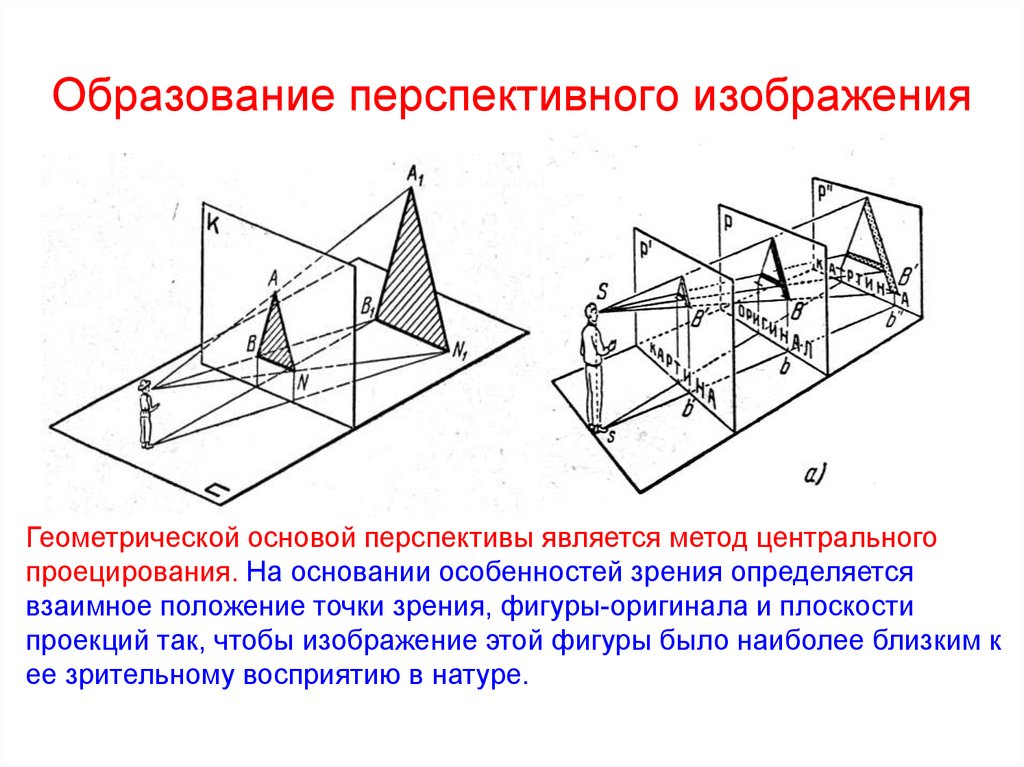
22. Образование перспективного изображения
Геометрической основой перспективы является метод центральногопроецирования. На основании особенностей зрения определяется
взаимное положение точки зрения, фигуры-оригинала и плоскости
проекций так, чтобы изображение этой фигуры было наиболее близким к
ее зрительному восприятию в натуре.
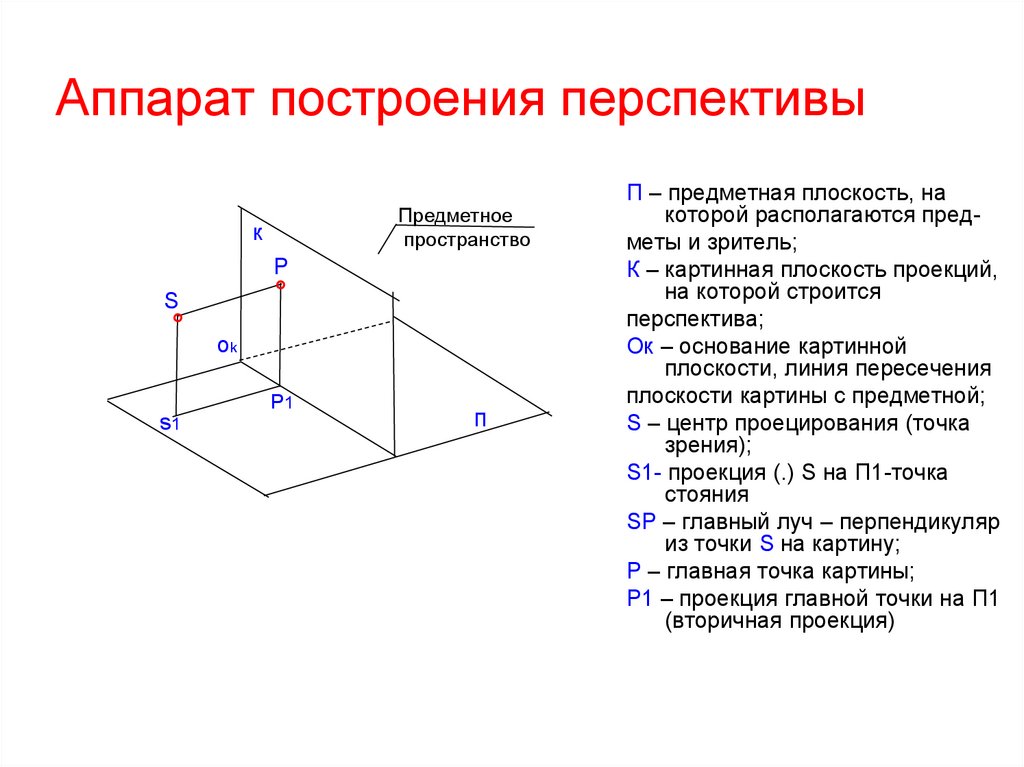
23. Аппарат построения перспективы
Предметноепространство
к
P
°
S
°
ok
P1
s1
п
П – предметная плоскость, на
которой располагаются предметы и зритель;
К – картинная плоскость проекций,
на которой строится
перспектива;
Ок – основание картинной
плоскости, линия пересечения
плоскости картины с предметной;
S – центр проецирования (точка
зрения);
S1- проекция (.) S на П1-точка
стояния
SР – главный луч – перпендикуляр
из точки S на картину;
Р – главная точка картины;
Р1 – проекция главной точки на П1
(вторичная проекция)
24. Аппарат построения перспективы
hк
P
°
S
°
Предметное
пространство
ok
h
P1
s1
п
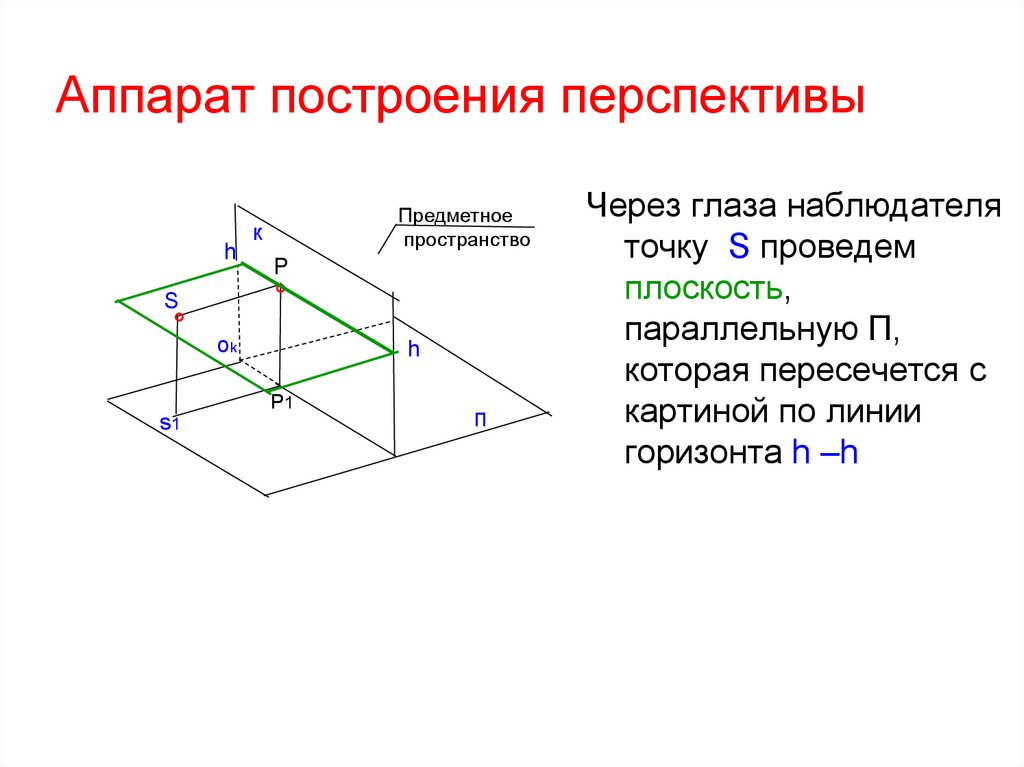
Через глаза наблюдателя
точку S проведем
плоскость,
параллельную П,
которая пересечется с
картиной по линии
горизонта h –h
25. Аппарат построения перспективы
D1h °
к
P
°
S
°
Предметное
пространство
D2
° h
ok
P1
s1
п
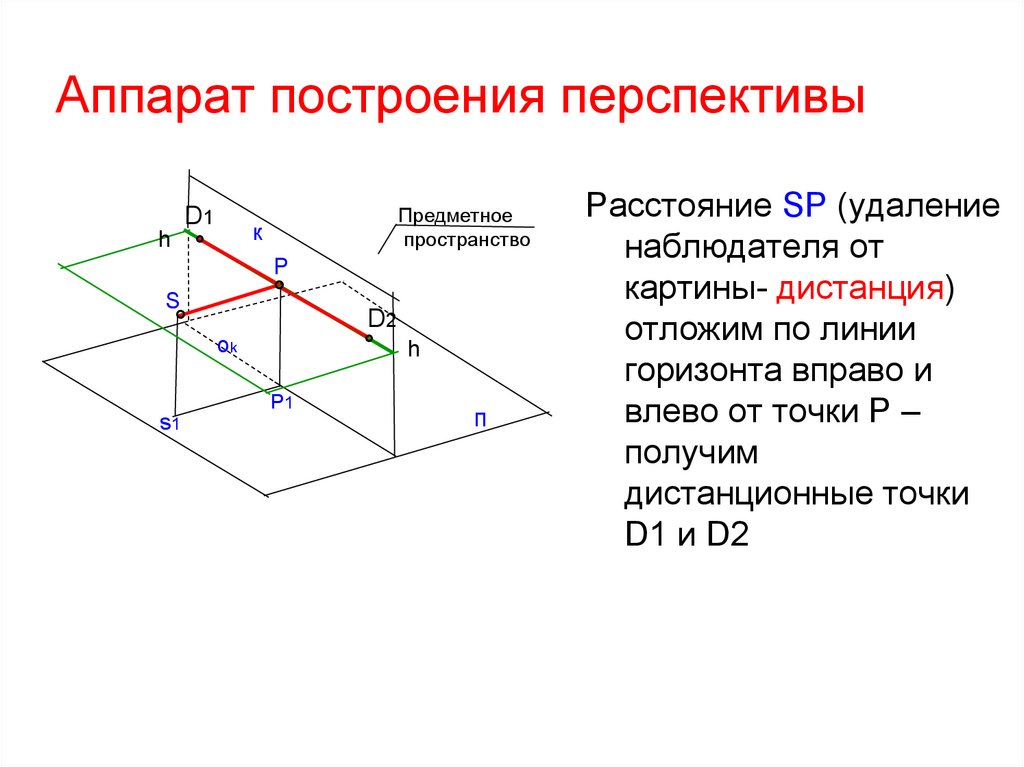
Расстояние SP (удаление
наблюдателя от
картины- дистанция)
отложим по линии
горизонта вправо и
влево от точки Р –
получим
дистанционные точки
D1 и D2
26. Аппарат построения перспективы
D1h °
к
45°
S
°
Предметное
пространство
P
°
45°
ok
P1
s1
D2
°
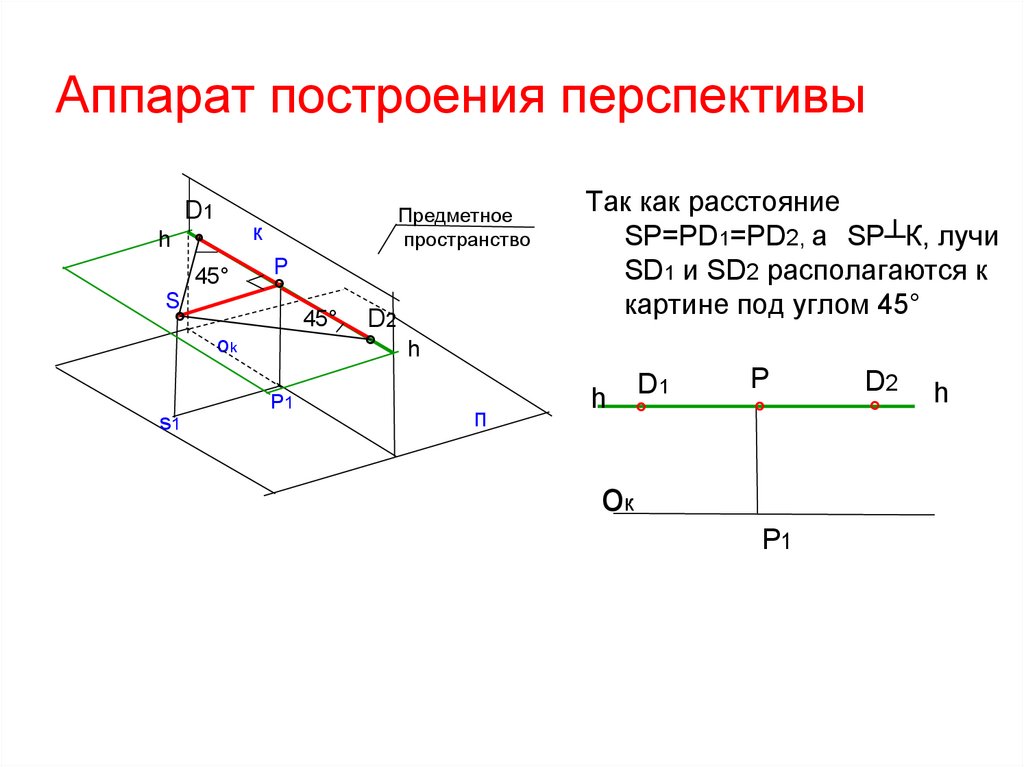
Так как расстояние
SP=PD1=PD2, а SP┴К, лучи
SD1 и SD2 располагаются к
картине под углом 45°
h
п
h
D1
°
P
°
ок
P1
D2
°
h
27. Виды перспектив
•Линейная- перспектива наплоскости
•Панорамная- перспектива на
внутренней поверхности цилиндра
•Купольная- перспектива на
внутренней поверхности сферы
28. Перспектива точки
hк
°
P
А
°
S
°
ok
h
P1
s1
п
°
А1
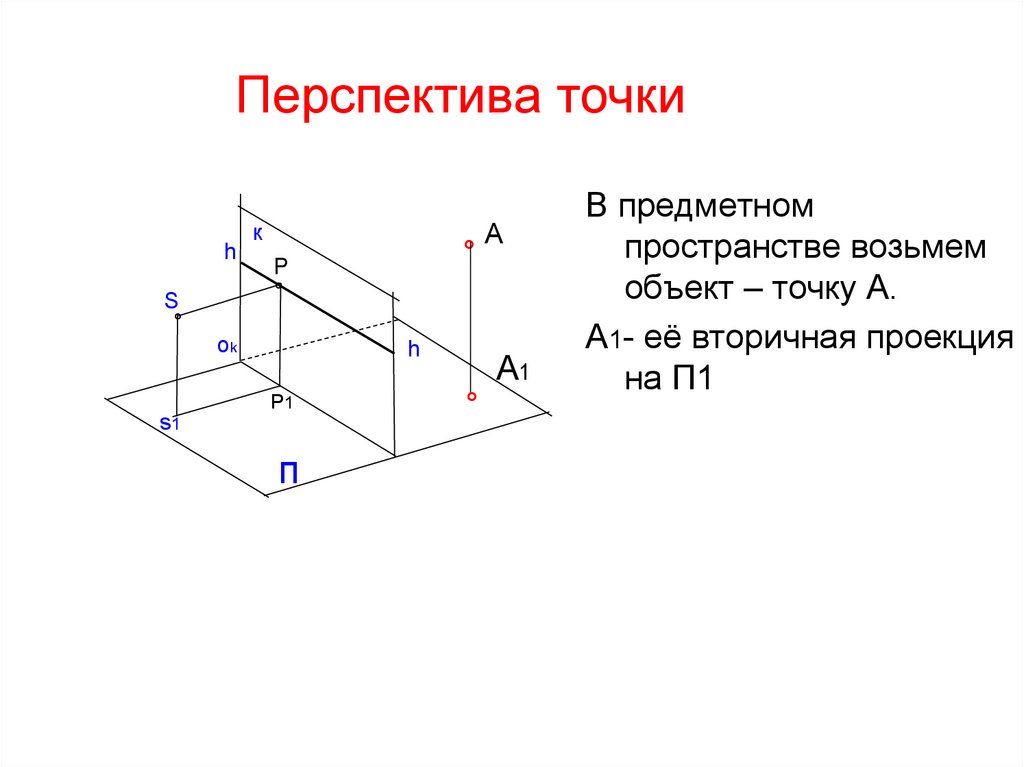
В предметном
пространстве возьмем
объект – точку А.
А1- её вторичная проекция
на П1
29. Перспектива точки
h°
P
А
°
S
°
к
ok
h
P1
s1
п
°
А1
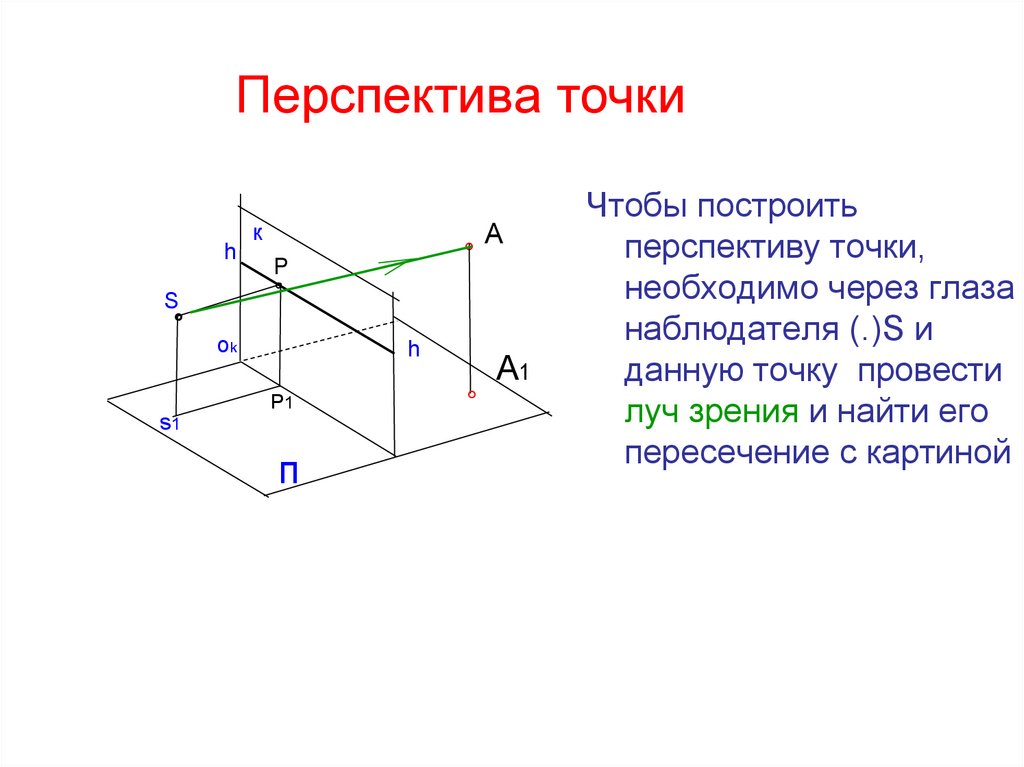
Чтобы построить
перспективу точки,
необходимо через глаза
наблюдателя (.)S и
данную точку провести
луч зрения и найти его
пересечение с картиной
30. Перспектива точки
hк
P
°
S
°
А'
°
А
°
ok
s°1
h
P1
п
°
А1
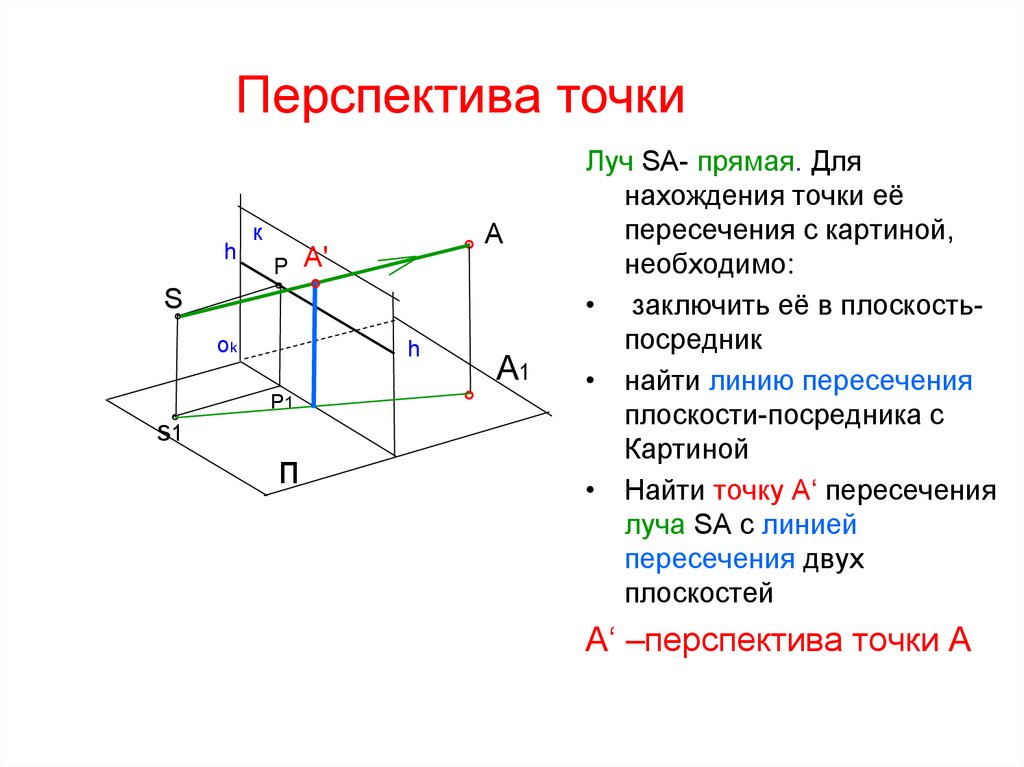
Луч SA- прямая. Для
нахождения точки её
пересечения с картиной,
необходимо:
• заключить её в плоскостьпосредник
• найти линию пересечения
плоскости-посредника с
Картиной
• Найти точку А‘ пересечения
луча SA с линией
пересечения двух
плоскостей
А‘ –перспектива точки А
31. Перспектива точки
hк
P
S
°
°
А'
°
А
°
ok
h
° А'1
°
P1
°
s1
п
h
Р
°
А'
° А'1
Р1
h
А1
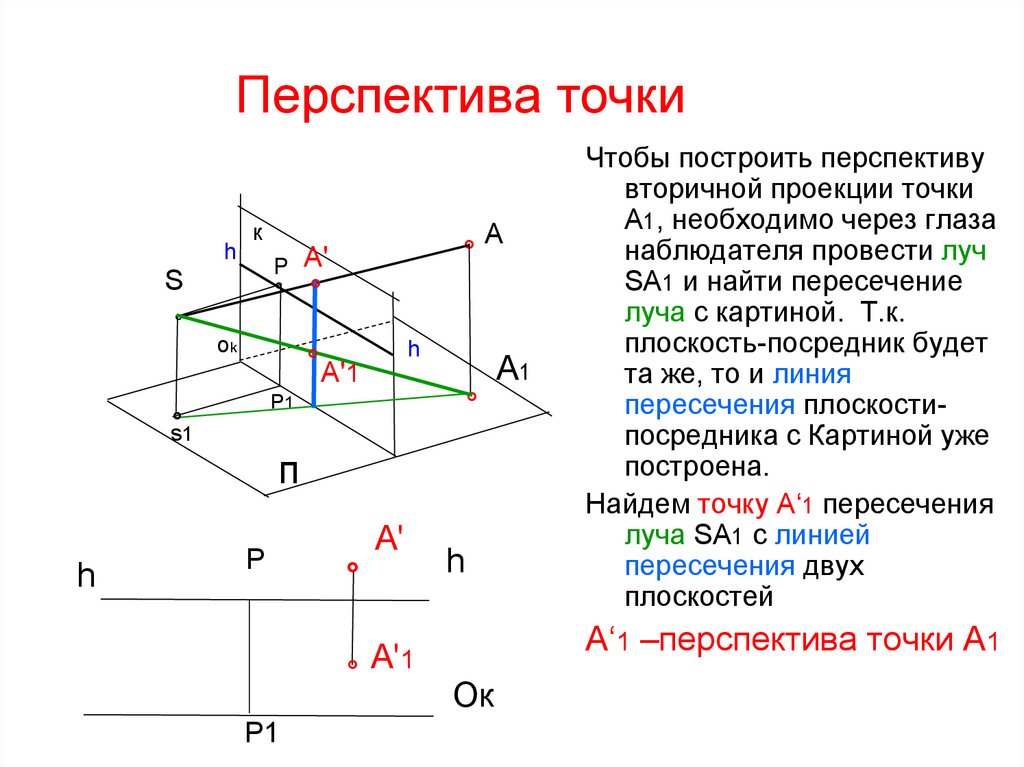
Чтобы построить перспективу
вторичной проекции точки
А1, необходимо через глаза
наблюдателя провести луч
SA1 и найти пересечение
луча с картиной. Т.к.
плоскость-посредник будет
та же, то и линия
пересечения плоскостипосредника с Картиной уже
построена.
Найдем точку А‘1 пересечения
луча SA1 с линией
пересечения двух
плоскостей
А‘1 –перспектива точки А1
Oк
32. Перспектива прямой
hк
P
°
S
°
ok
s1°
h
P1
п
а≡а1
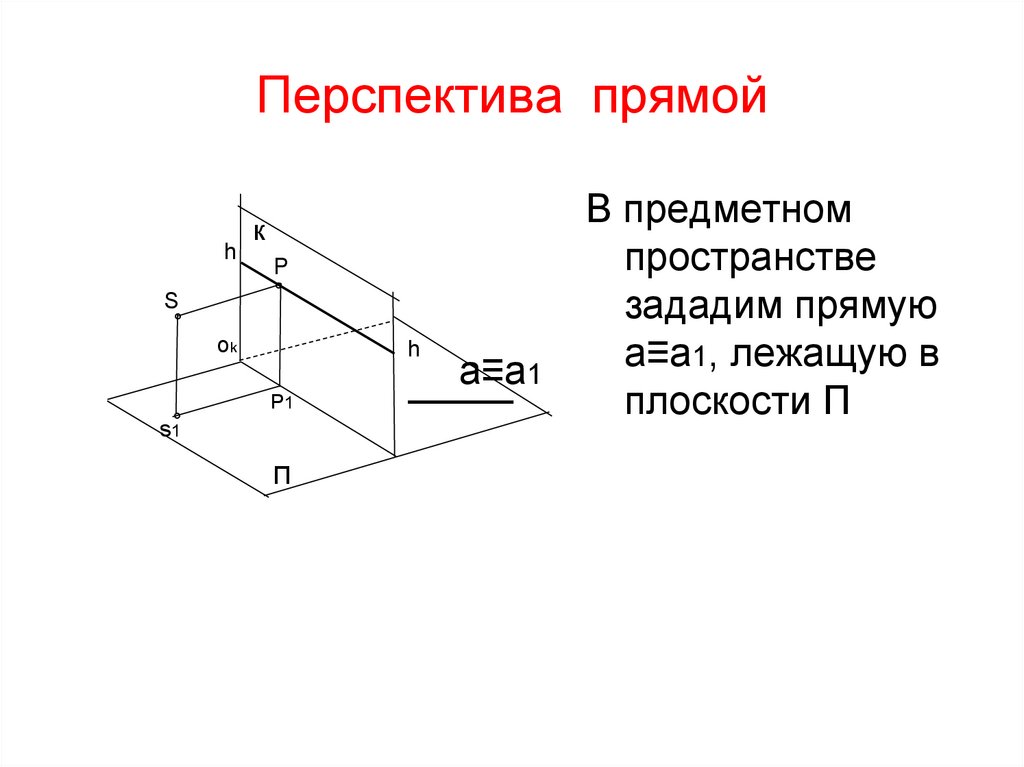
В предметном
пространстве
зададим прямую
а≡а1, лежащую в
плоскости П
33. Перспектива прямой
hP
°
S
°
к
ok
h
P1
s1
п
°Ак
а≡а1
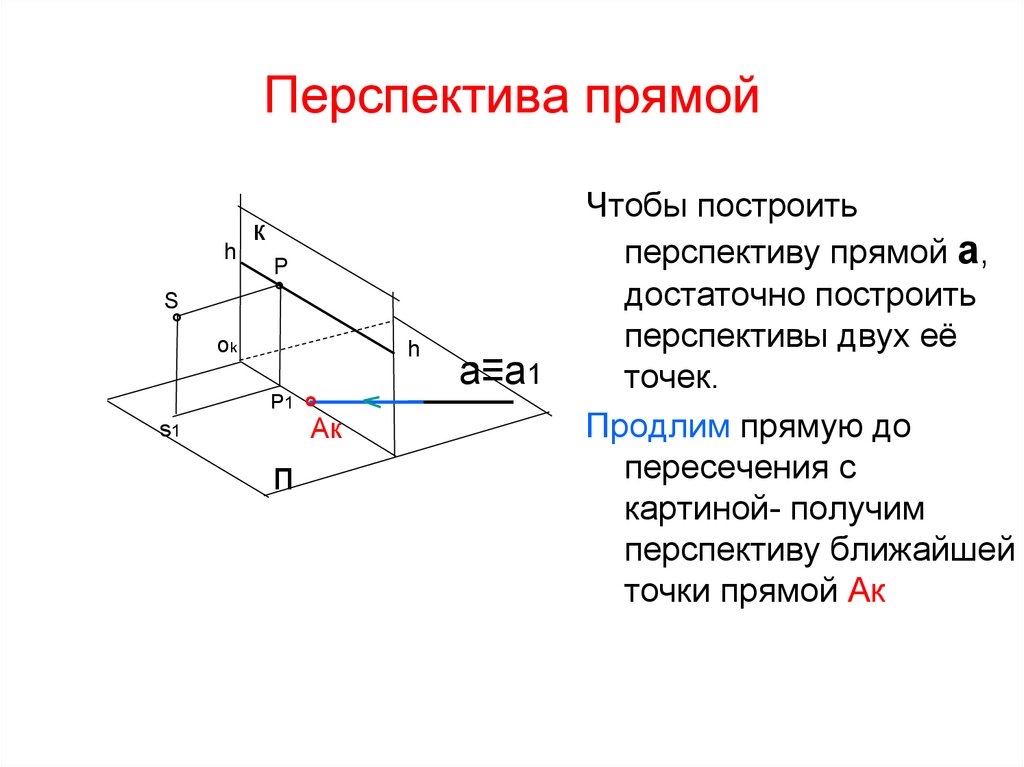
Чтобы построить
перспективу прямой а,
достаточно построить
перспективы двух её
точек.
Продлим прямую до
пересечения с
картиной- получим
перспективу ближайшей
точки прямой Ак
34. Перспектива прямой
hS
°
к
P
°
ok
P1
s1
А∞
°
°Ак
h
а≡а1
п
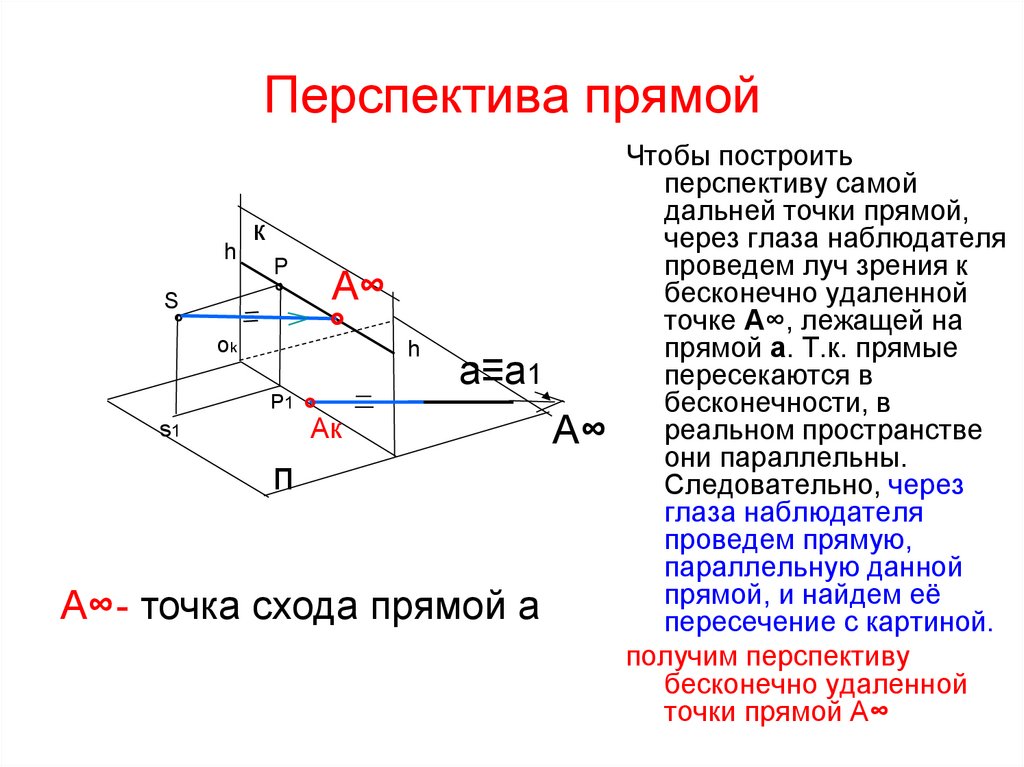
А∞- точка схода прямой а
А∞
Чтобы построить
перспективу самой
дальней точки прямой,
через глаза наблюдателя
проведем луч зрения к
бесконечно удаленной
точке А∞, лежащей на
прямой а. Т.к. прямые
пересекаются в
бесконечности, в
реальном пространстве
они параллельны.
Следовательно, через
глаза наблюдателя
проведем прямую,
параллельную данной
прямой, и найдем её
пересечение с картиной.
получим перспективу
бесконечно удаленной
точки прямой А∞
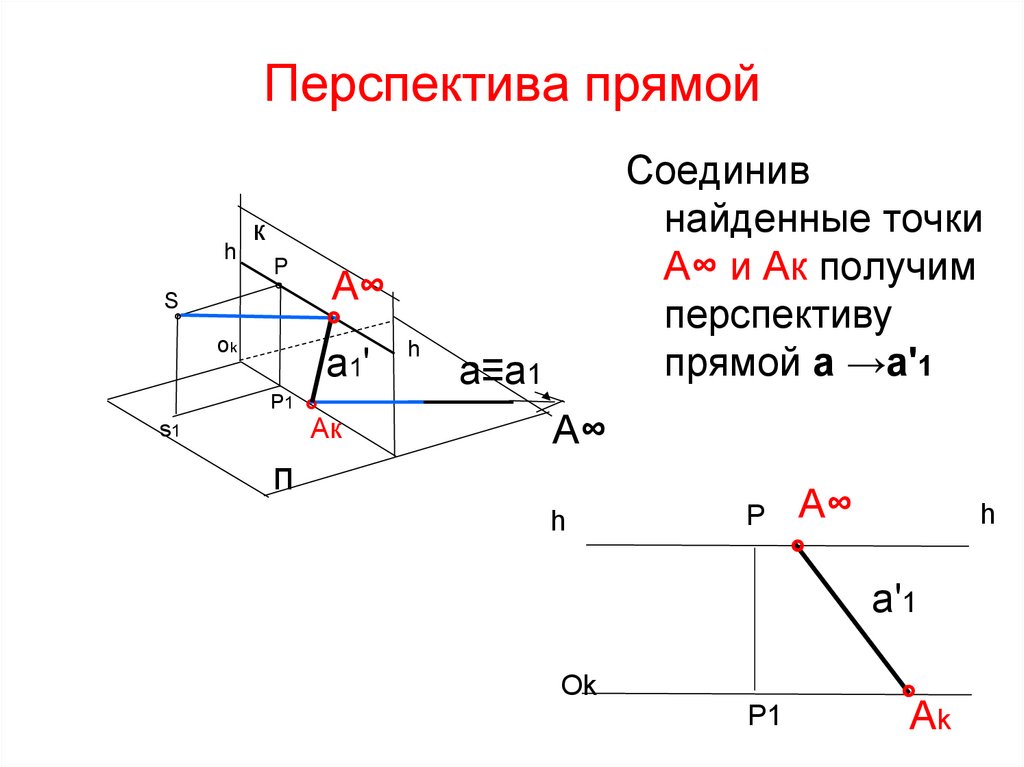
35. Перспектива прямой
hк
P
°
S
Соединив
найденные точки
А∞ и Ак получим
перспективу
прямой а →a'1
°
ok
P1
s1
А∞
°
а1'
°Ак
h
а≡а1
А∞
п
h
P
А∞
°
h
a'1
Ok
P1
°Ak
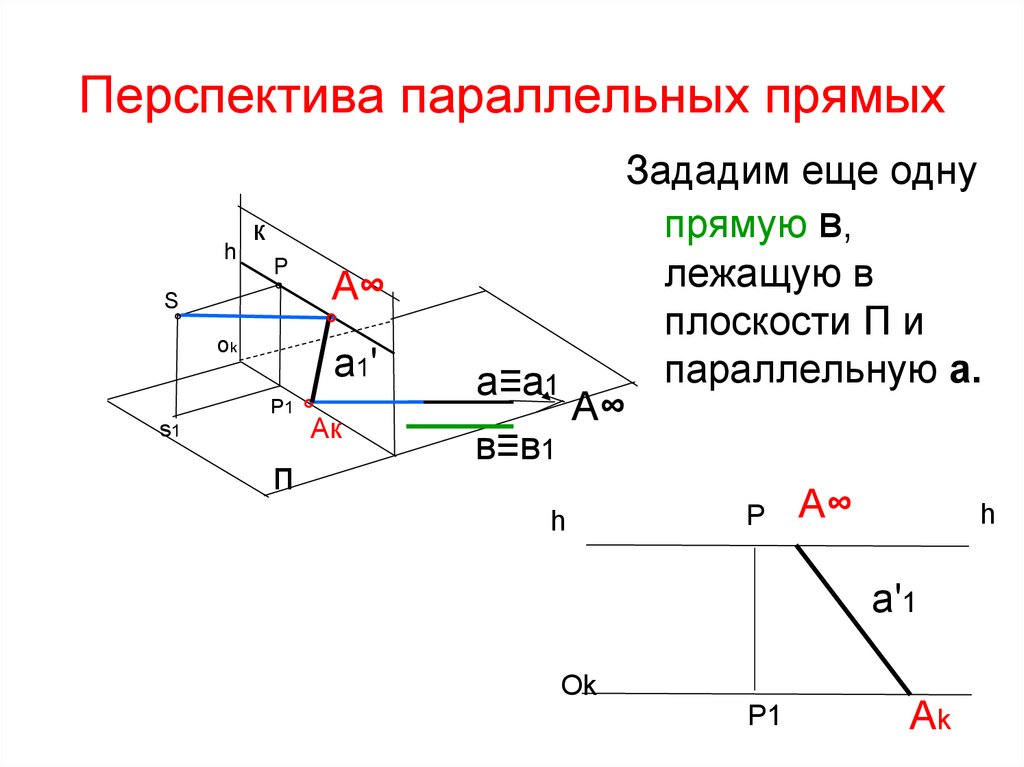
36. Перспектива параллельных прямых
hк
P
°
S
А∞
°
°
ok
а1'
P1
s1
п
°
Ак
Зададим еще одну
прямую в,
лежащую в
плоскости П и
параллельную а.
а≡а1
А∞
в≡в1
h
P А∞
h
a'1
Ok
P1
Ak
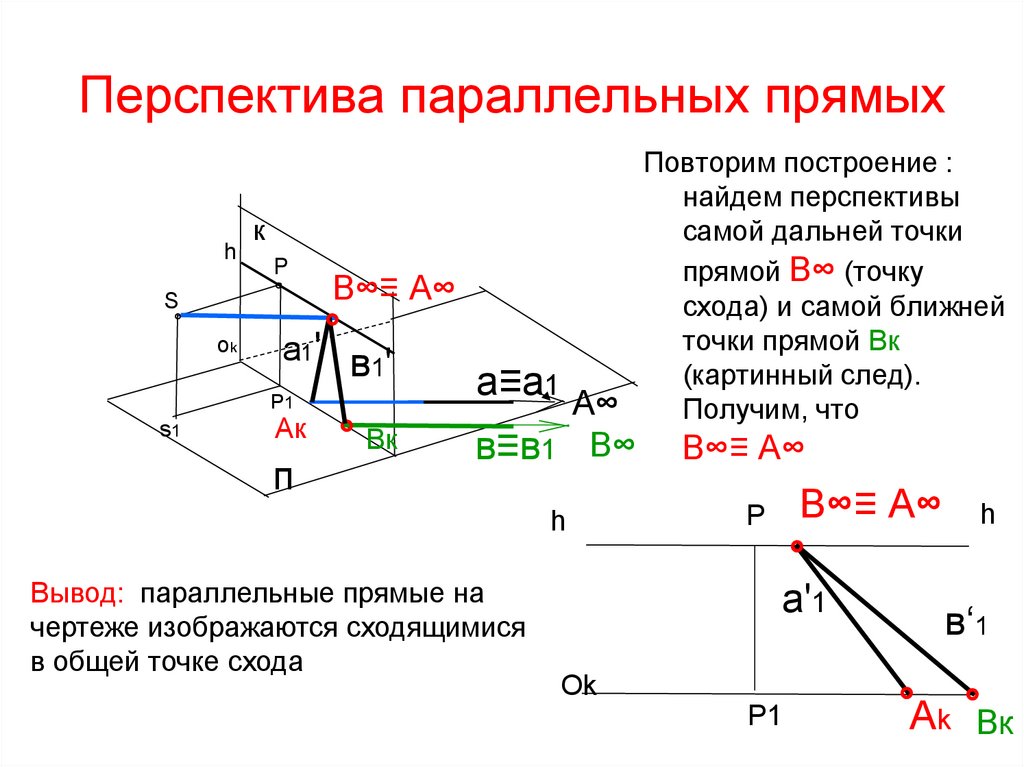
37. Перспектива параллельных прямых
hS
°
ok
s1
Повторим построение :
найдем перспективы
к
самой дальней точки
P
прямой В∞ (точку
°
В∞≡ А∞
схода) и самой ближней
°
точки прямой Вк
а1' в1'
(картинный след).
а≡а
1
P1
А∞
Получим, что
Ак ° Вк
в≡в1 В∞ В∞≡ А∞
п
h
Вывод: параллельные прямые на
чертеже изображаются сходящимися
в общей точке схода
P
В∞≡ А∞
°
a'1
Ok
P1
h
в‘1
°Ak °Вк
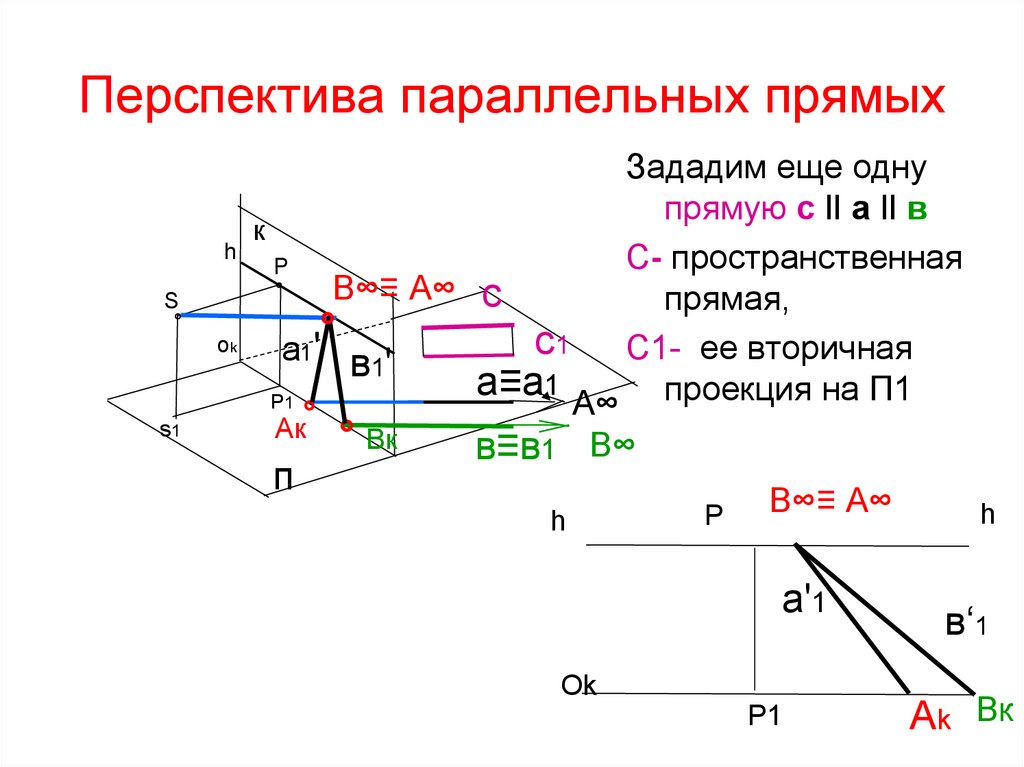
38. Перспектива параллельных прямых
hS
°
ok
s1
Зададим еще одну
прямую с ‖ а ‖ в
к
С- пространственная
P
°
В∞≡ А∞ с
прямая,
°
с1 С1- ее вторичная
а1' в1'
а≡а1
проекция на П1
P1
А∞
Ак° ° Вк
в≡в1 В∞
п
h
P
В∞≡ А∞
a'1
Ok
P1
h
в‘1
Ak Вк
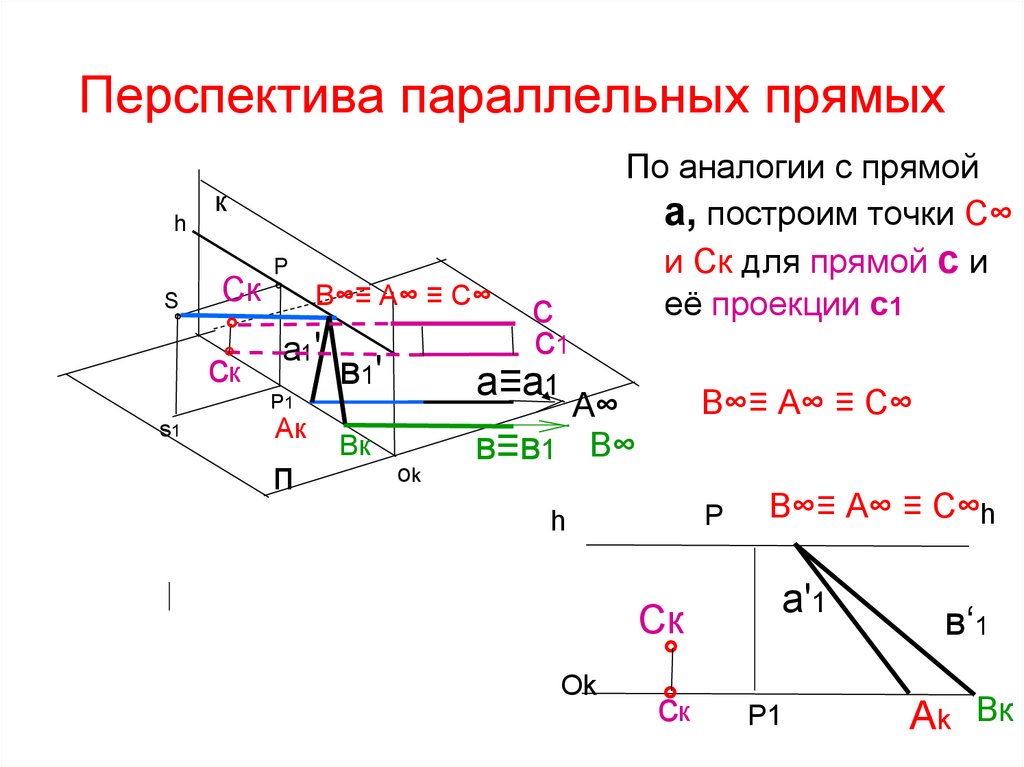
39. Перспектива параллельных прямых
hS
°
к
Ск
°
с°к
P
°
В∞≡ А∞ ≡ С∞
а1'
с
с1
а≡а1
в1'
P1
s1
Ак
п
Вк
ok
По аналогии с прямой
а, построим точки С∞
и Ск для прямой с и
её проекции с1
В∞≡ А∞ ≡ С∞
А∞
в≡в1 В∞
P
h
Ok
Ск
°
с°к
В∞≡ А∞ ≡ С∞h
a'1
P1
в‘1
Ak Вк
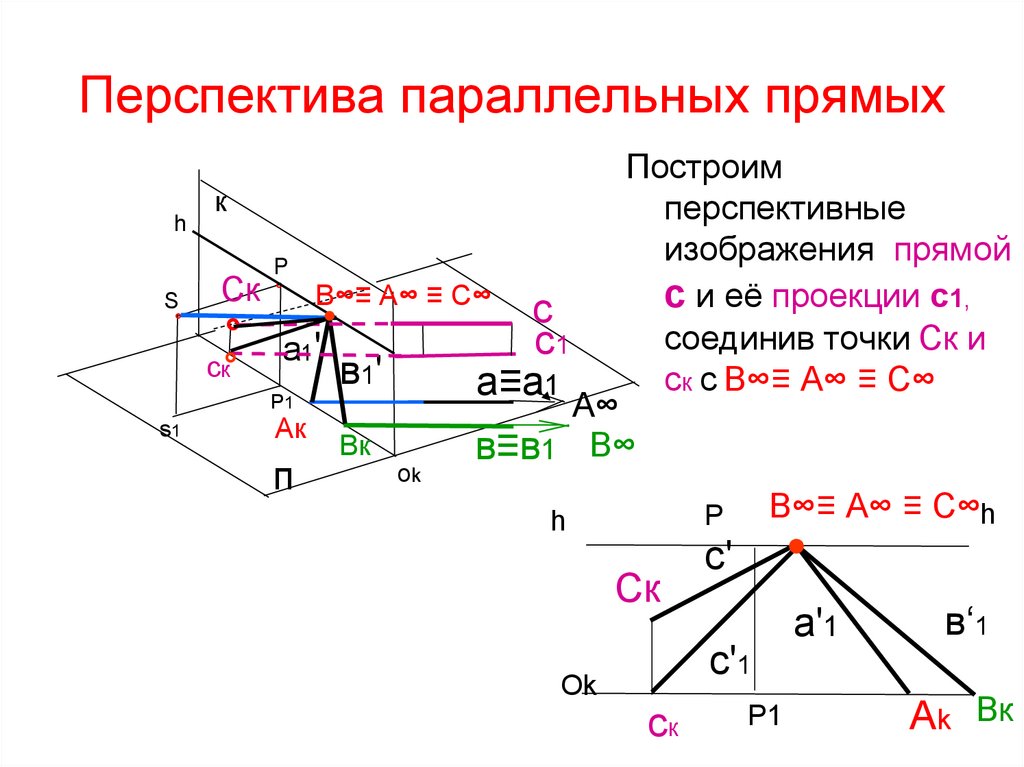
40. Перспектива параллельных прямых
hS
°
к
Ск
°
ск°
P
°
В∞≡ А∞ ≡ С∞
с
с1
а≡а1
а1'
в1'
P1
s1
Ак
п
Вк
ok
Построим
перспективные
изображения прямой
с и её проекции с1,
соединив точки Ск и
ск с В∞≡ А∞ ≡ С∞
А∞
в≡в1 В∞
Ск
Ok
В∞≡ А∞ ≡ С∞h
P
h
с'
с'1
ск
P1
a'1
в‘1
Ak Вк
41. Параллельные прямые имеют общую точку схода. Точка схода- перспектива бесконечно удаленной точки прямой. Чтобы построить точку
сходапрямой, необходимо через глаза
наблюдателя провести прямую,
параллельную данной прямой и
найти ее пересечение с картиной
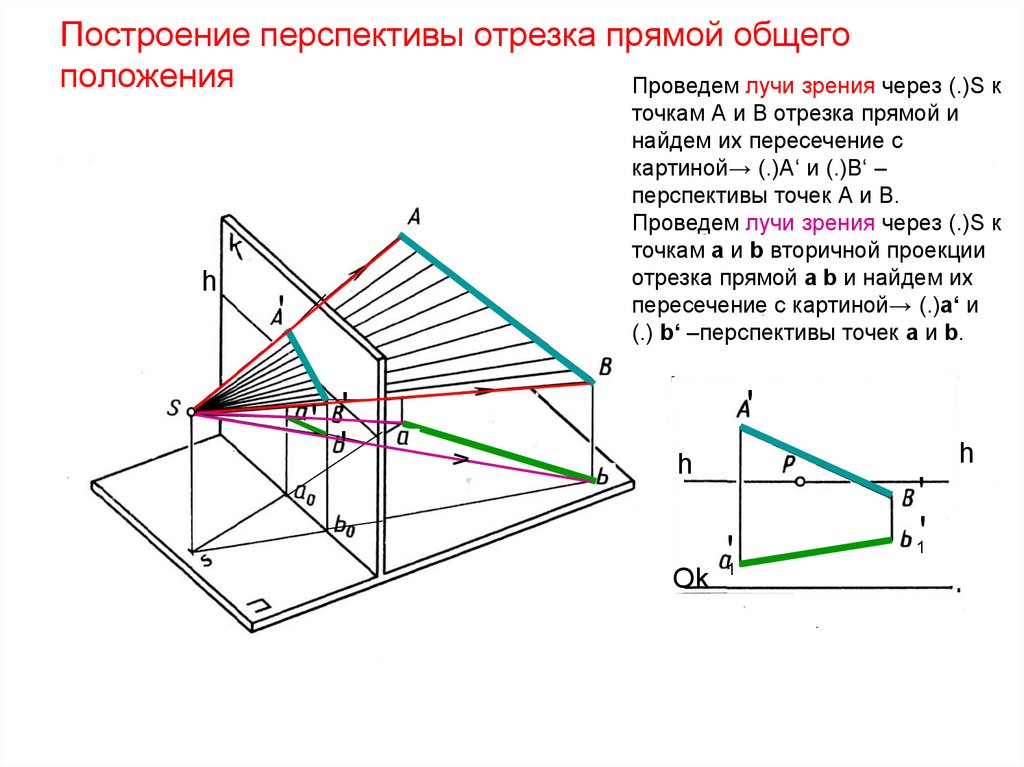
42. Построение перспективы отрезка прямой общего положения
Проведем лучи зрения через (.)S кh
точкам А и В отрезка прямой и
найдем их пересечение с
картиной→ (.)А‘ и (.)В‘ –
перспективы точек А и В.
Проведем лучи зрения через (.)S к
точкам a и b вторичной проекции
отрезка прямой а b и найдем их
пересечение с картиной→ (.)а‘ и
(.) b‘ –перспективы точек а и b.
'
' '
'
'
h
h
Ok
'
1
'
'
1
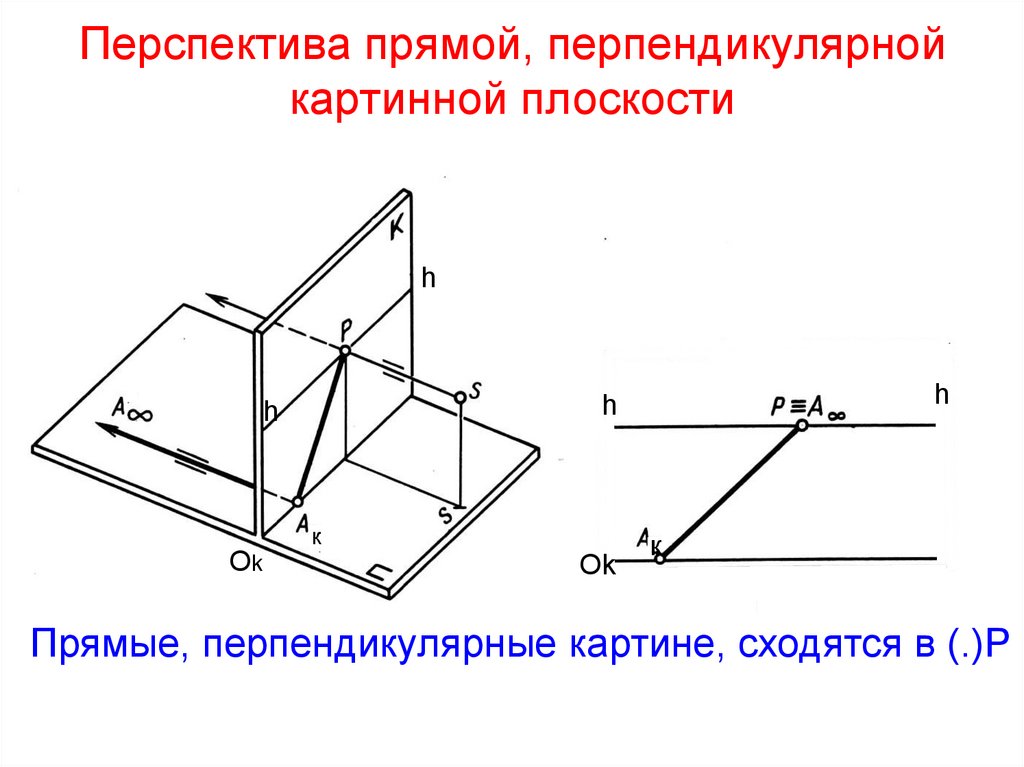
43. Перспектива прямой, перпендикулярной картинной плоскости
hк
Ok
h
h
h
Ok
к
Прямые, перпендикулярные картине, сходятся в (.)Р
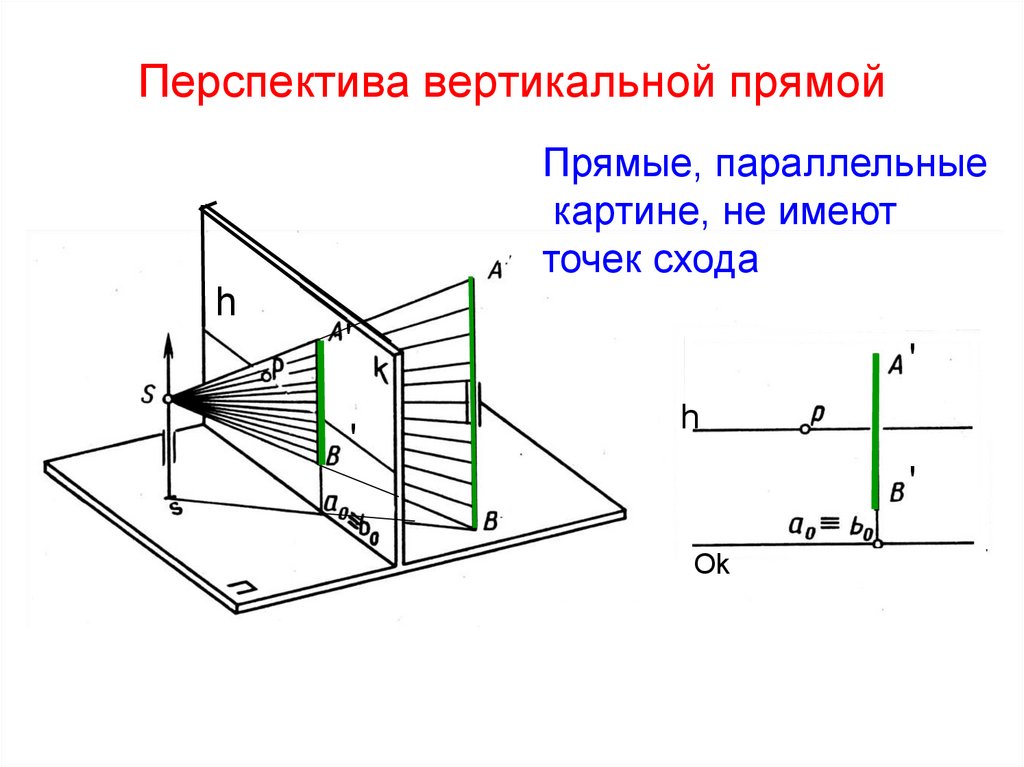
44. Перспектива вертикальной прямой
Прямые, параллельныекартине, не имеют
точек схода
h
'
'
'
h
'
Ok
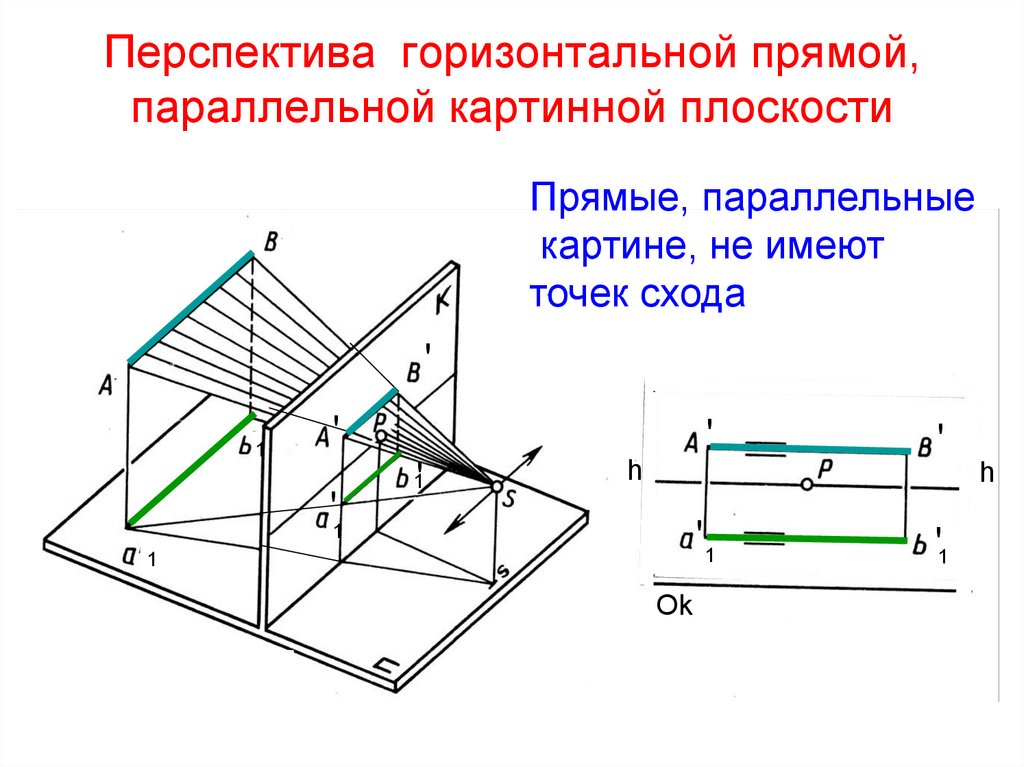
45. Перспектива горизонтальной прямой, параллельной картинной плоскости
Прямые, параллельныекартине, не имеют
точек схода
'
1
'
'1
'
'
1
h
'
h
'1
1
Ok
'1
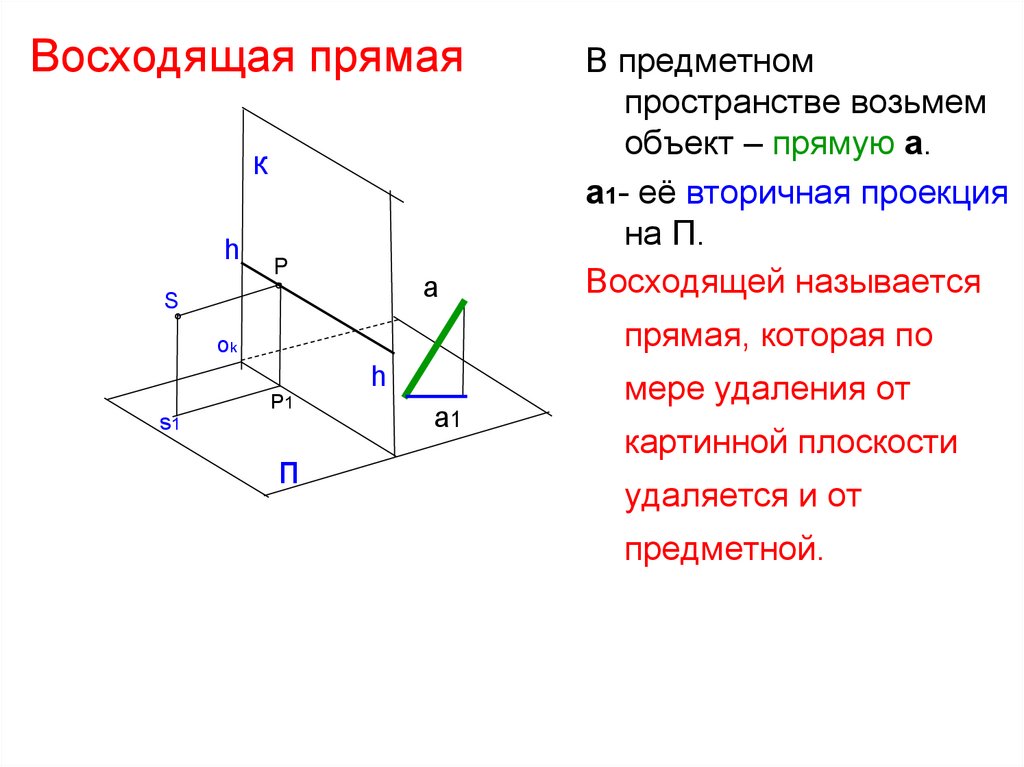
46. Восходящая прямая
кh
P
а
°
S
°
В предметном
пространстве возьмем
объект – прямую а.
а1- её вторичная проекция
на П.
Восходящей называется
прямая, которая по
ok
h
P1
s1
п
а1
мере удаления от
картинной плоскости
удаляется и от
предметной.
47.
А∞к
°
h
P
°
S
°
ok
P1
s1
п
°
а∞
а
h
а1
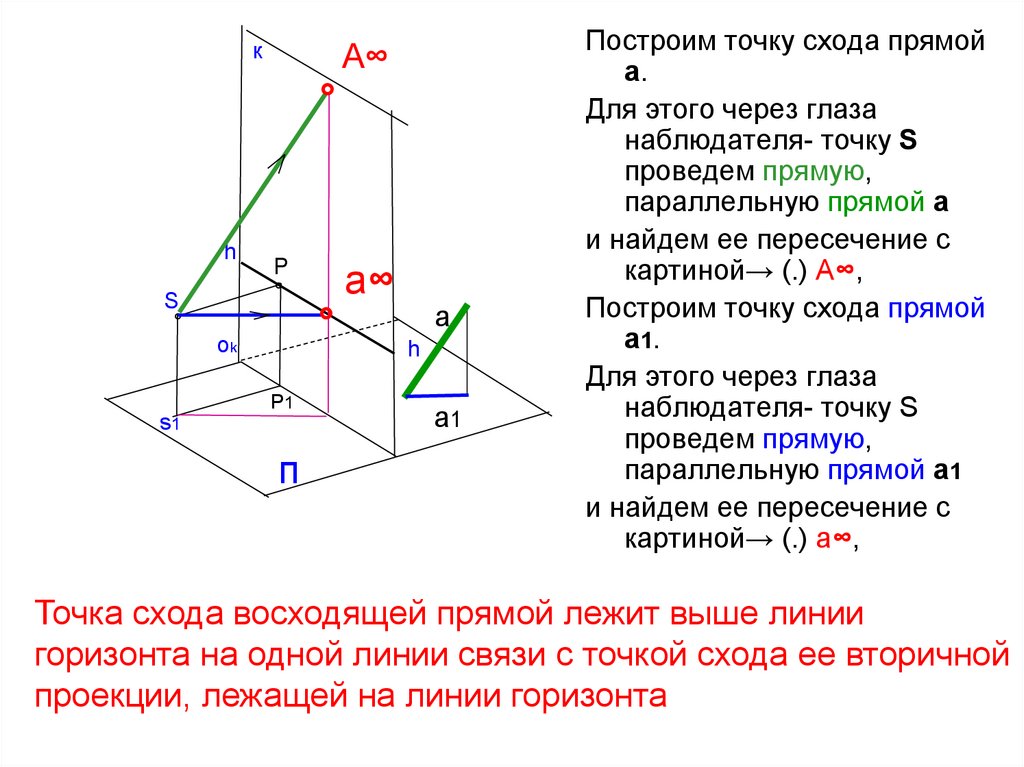
Построим точку схода прямой
а.
Для этого через глаза
наблюдателя- точку S
проведем прямую,
параллельную прямой а
и найдем ее пересечение с
картиной→ (.) А∞,
Построим точку схода прямой
а 1.
Для этого через глаза
наблюдателя- точку S
проведем прямую,
параллельную прямой а1
и найдем ее пересечение с
картиной→ (.) а∞,
Точка схода восходящей прямой лежит выше линии
горизонта на одной линии связи с точкой схода ее вторичной
проекции, лежащей на линии горизонта
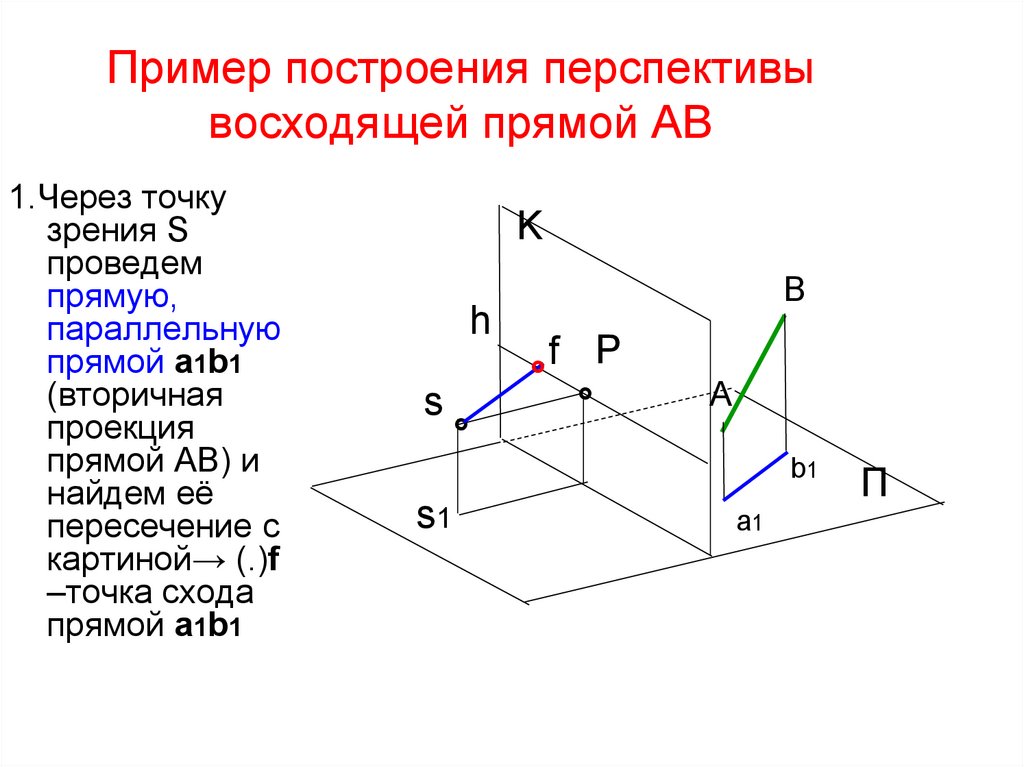
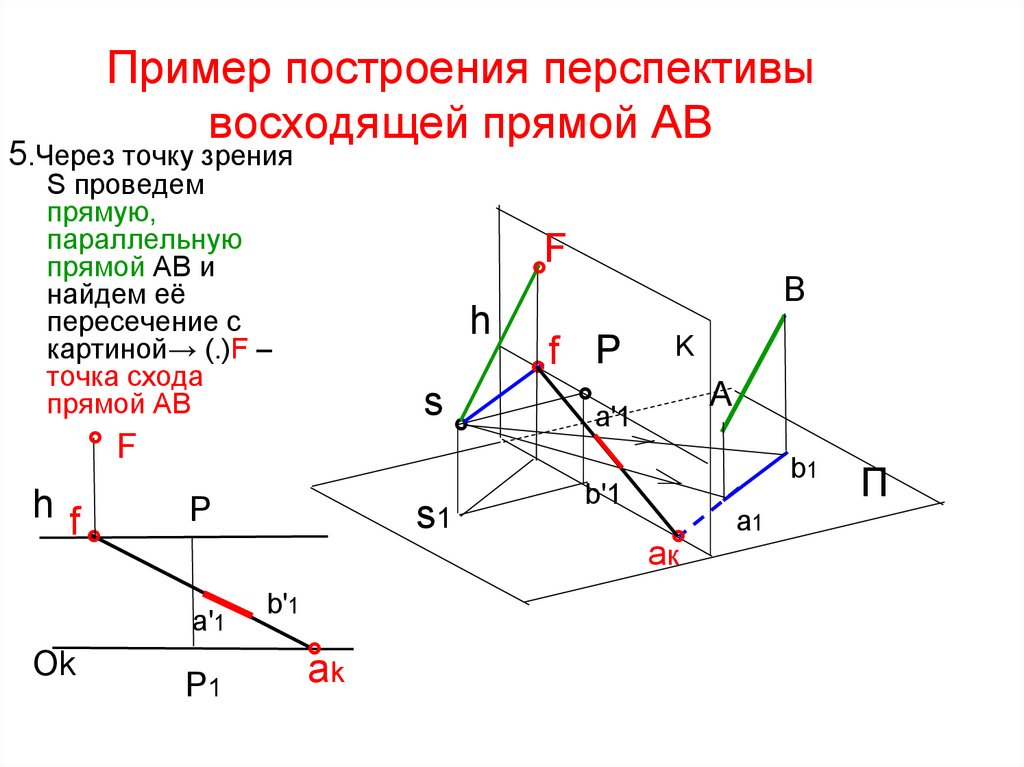
48. Пример построения перспективы восходящей прямой AB
1.Через точкузрения S
проведем
прямую,
параллельную
прямой a1b1
(вторичная
проекция
прямой АВ) и
найдем её
пересечение с
картиной→ (.)f
–точка схода
прямой a1b1
K
h
s
°
B
f P
°
°
A
b1
s1
а1
П
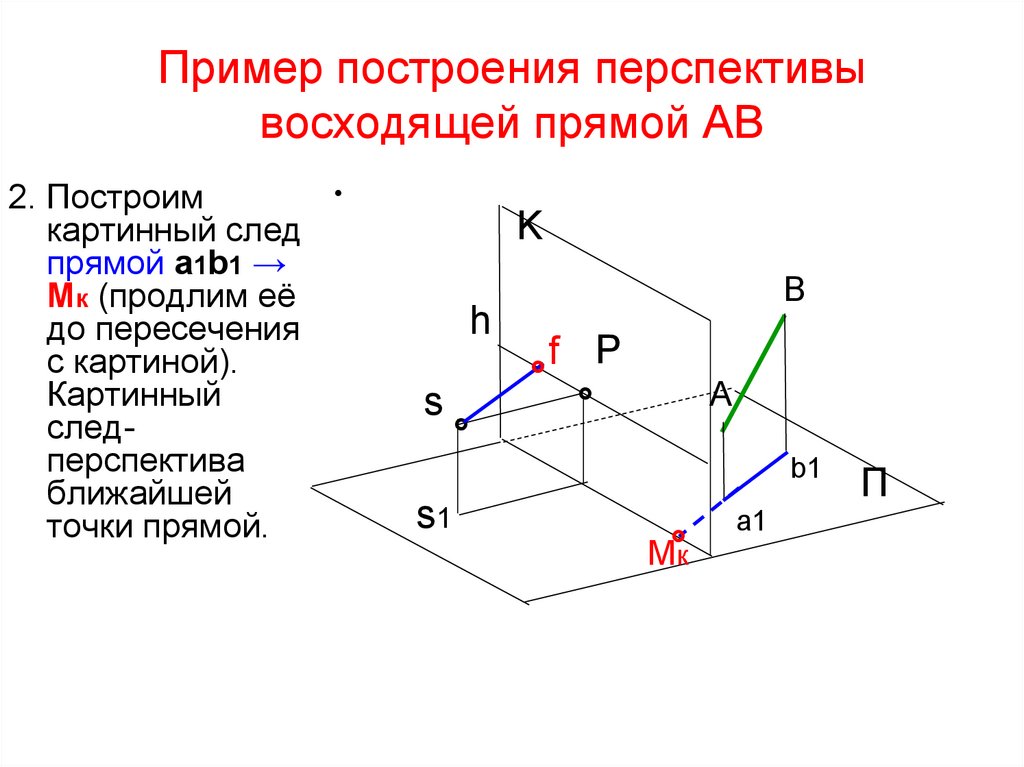
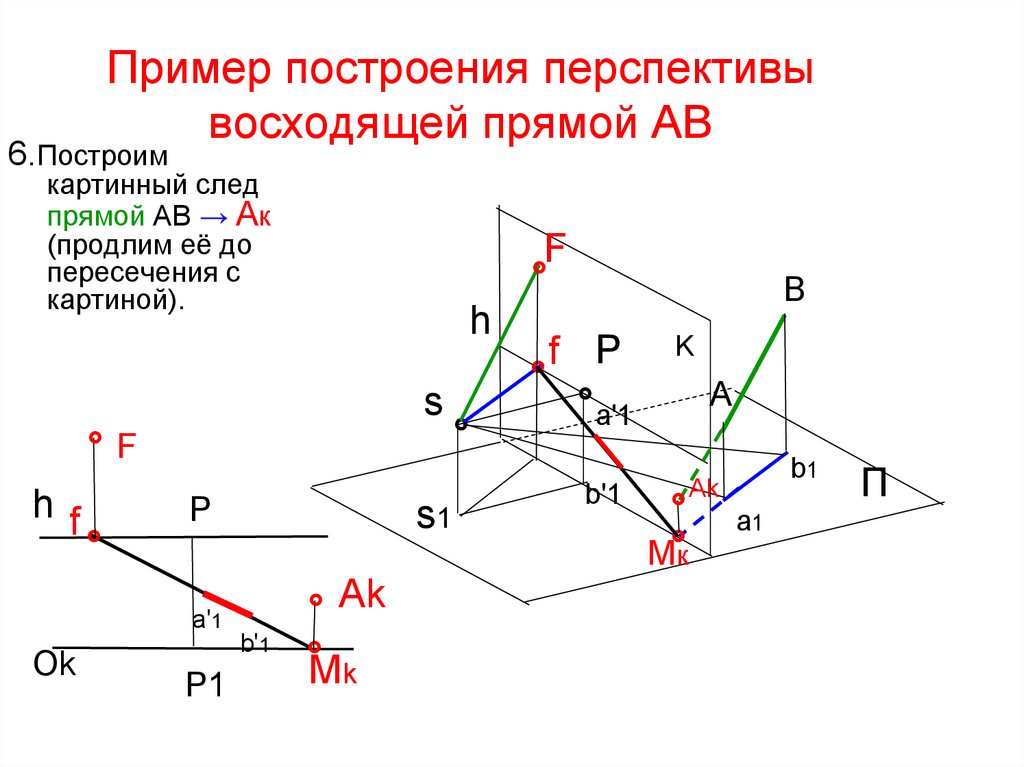
49. Пример построения перспективы восходящей прямой AB
2. Построимкартинный след
прямой а1b1 →
Mк (продлим её
до пересечения
с картиной).
Картинный
следперспектива
ближайшей
точки прямой.
K
h
s
°
B
f P
°
°
A
b1
s1
M°к
а1
П
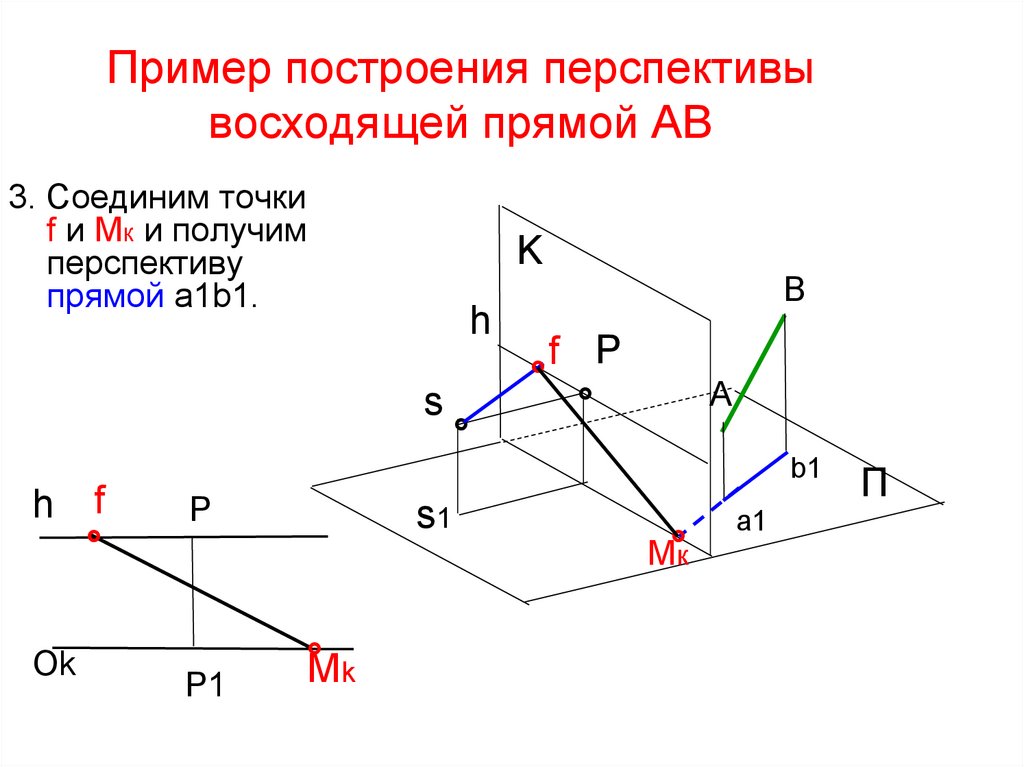
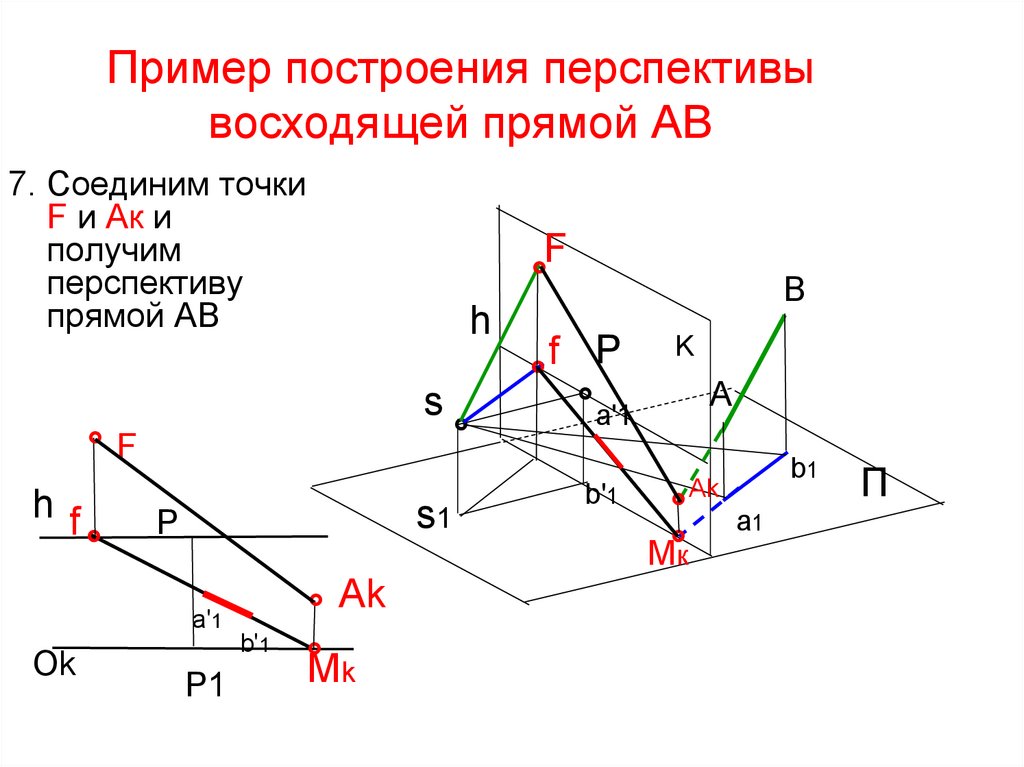
50. Пример построения перспективы восходящей прямой AB
3. Соединим точкиf и Mк и получим
перспективу
прямой а1b1.
K
h
s
°
B
f P
°
°
A
b1
h f
°
Ok
P
P1
s1
°Mk
M°к
а1
П
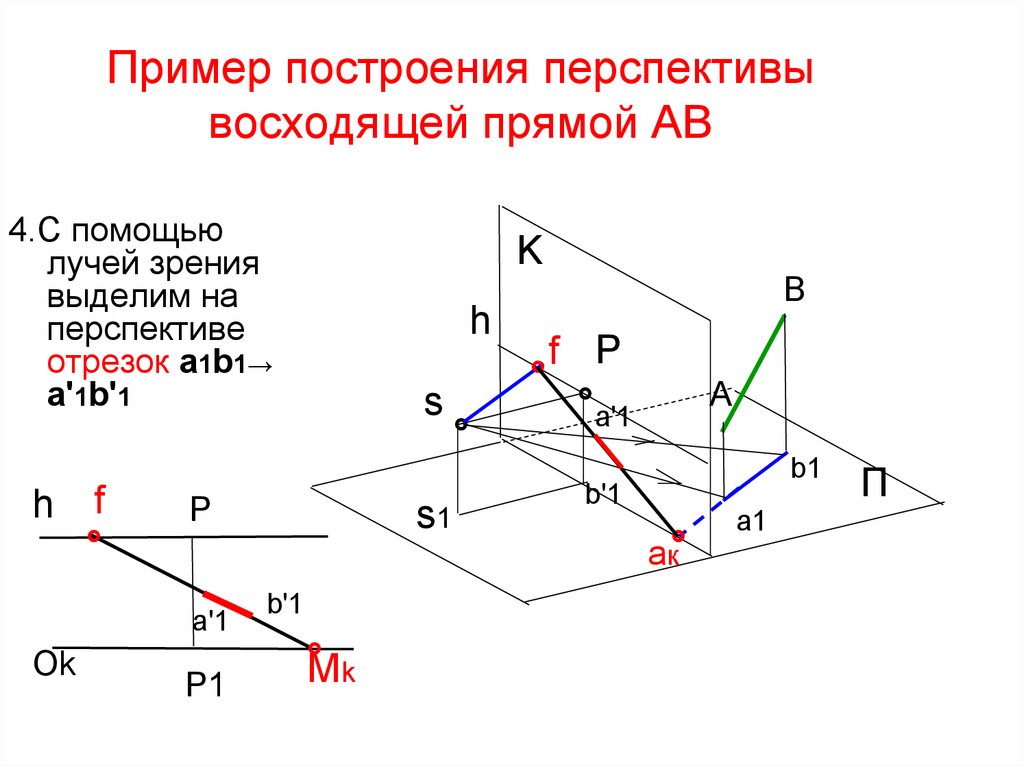
51. Пример построения перспективы восходящей прямой AB
4.С помощьюлучей зрения
выделим на
перспективе
отрезок а1b1→
а'1b'1
h f
°
h
s
P
а'1
Ok
K
P1
s1
b'1
°Mk
°
B
f P
°
°а'1
A
b1
b'1
ак°
а1
П
52. Пример построения перспективы восходящей прямой AB
5.Через точку зренияS проведем
прямую,
параллельную
прямой AB и
найдем её
пересечение с
картиной→ (.)F –
точка схода
прямой AB
F
°
h
s
°F
hf
°
P
а'1
Ok
P1
s1
b'1
°ak
°
B
f P
°
°а'1
K
A
b1
b'1
ак°
а1
П
53. Пример построения перспективы восходящей прямой AB
6.Построимкартинный след
прямой AB → Aк
(продлим её до
пересечения с
картиной).
F
°
h
s
°F
hf
°
P
s1
а'1
Ok
b'1
P1
° Ak
°Mk
°
B
f P
°
° а'1
b'1
K
A
°
M°к
b1
Ak
а1
П
54. Пример построения перспективы восходящей прямой AB
7. Соединим точкиF и Aк и
получим
перспективу
прямой AB
F
°
h
s
°F
hf
°
s1
P
а'1
Ok
b'1
P1
° Ak
°Mk
°
B
f P
°
° а'1
b'1
K
A
°
M°к
b1
Ak
а1
П
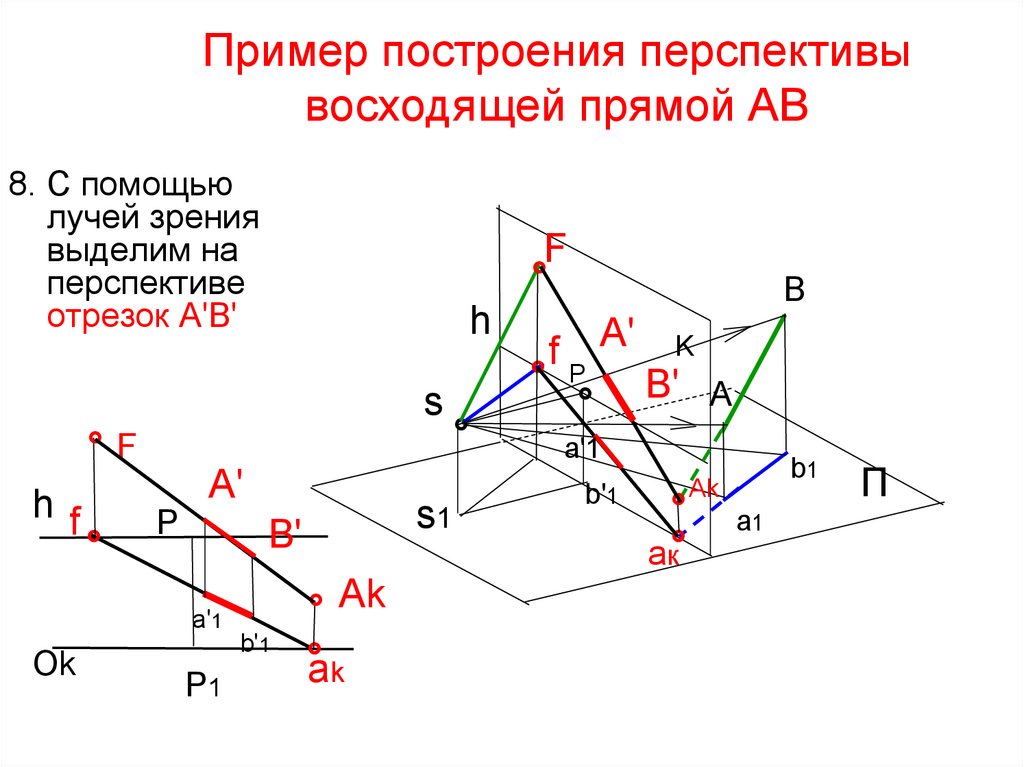
55. Пример построения перспективы восходящей прямой AB
8. С помощьюлучей зрения
выделим на
перспективе
отрезок A'B'
F
°
h
s
°F
hf
A'
°
P
B'
а'1
Ok
s1
b'1
P1
° Ak
°ak
°
B
f P A' K
°
° B' A
а'1
b'1
°
ак°
b1
Ak
а1
П
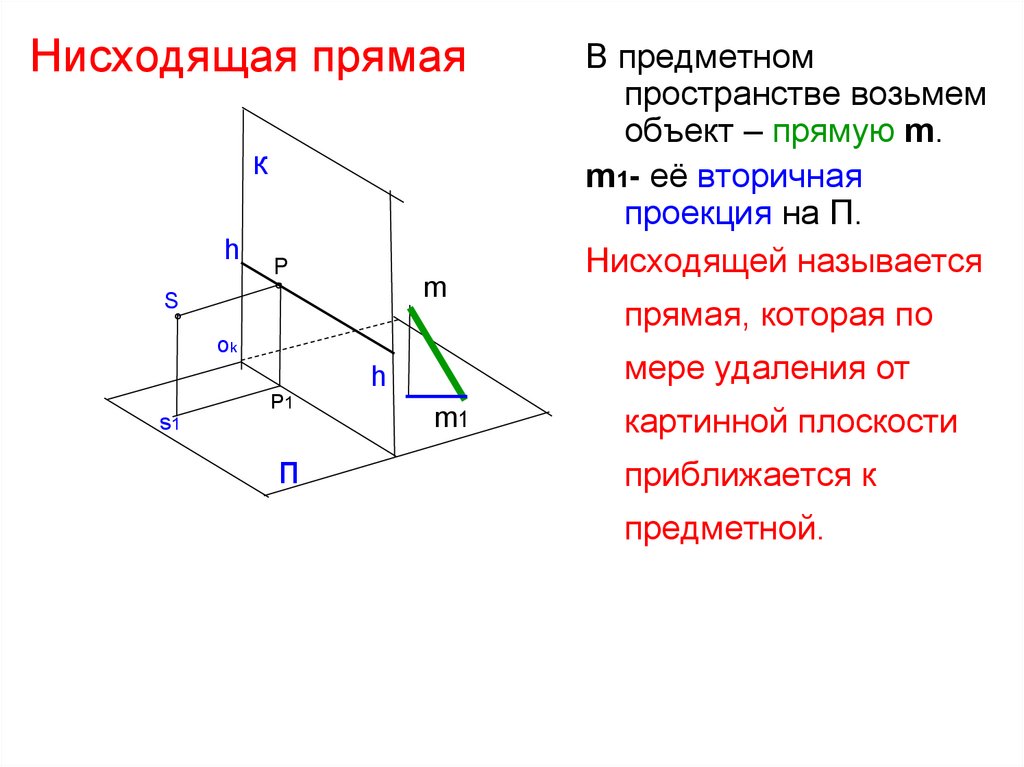
56. Нисходящая прямая
кh
P
m
°
S
°
ok
s1
п
прямая, которая по
мере удаления от
h
P1
В предметном
пространстве возьмем
объект – прямую m.
m1- её вторичная
проекция на П.
Нисходящей называется
m1
картинной плоскости
приближается к
предметной.
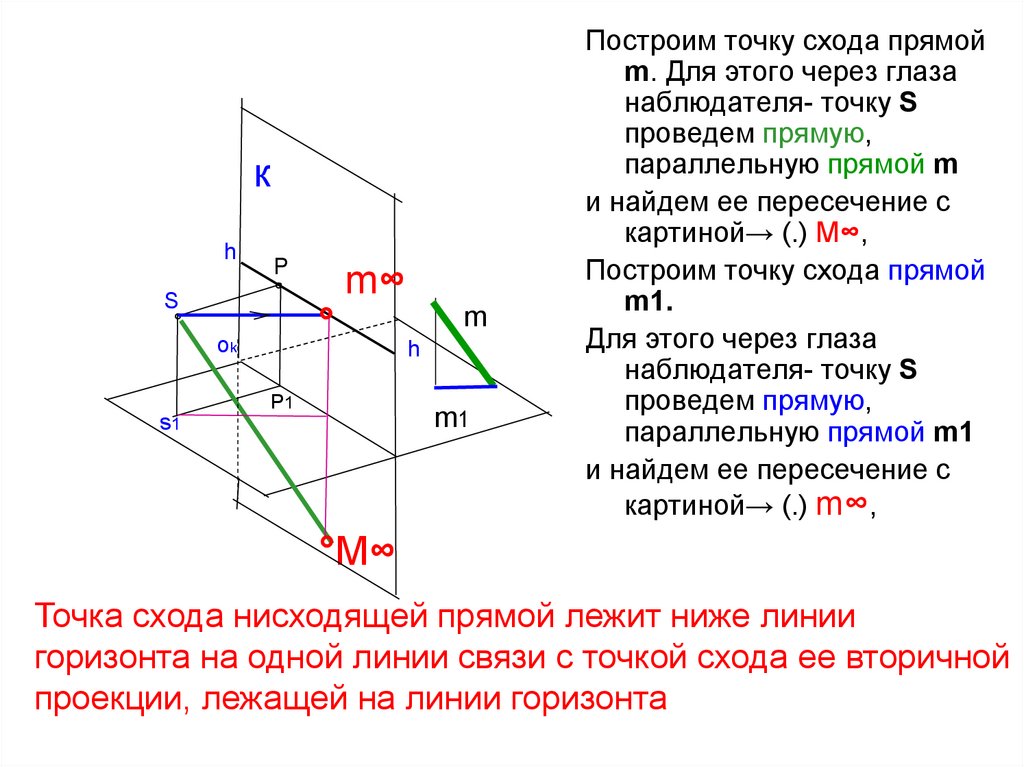
57.
кh
P
°
S
°
ok
°
m∞
P1
m
h
m1
s1
Построим точку схода прямой
m. Для этого через глаза
наблюдателя- точку S
проведем прямую,
параллельную прямой m
и найдем ее пересечение с
картиной→ (.) М∞,
Построим точку схода прямой
m1.
Для этого через глаза
наблюдателя- точку S
проведем прямую,
параллельную прямой m1
и найдем ее пересечение с
картиной→ (.) m∞,
°М∞
Точка схода нисходящей прямой лежит ниже линии
горизонта на одной линии связи с точкой схода ее вторичной
проекции, лежащей на линии горизонта
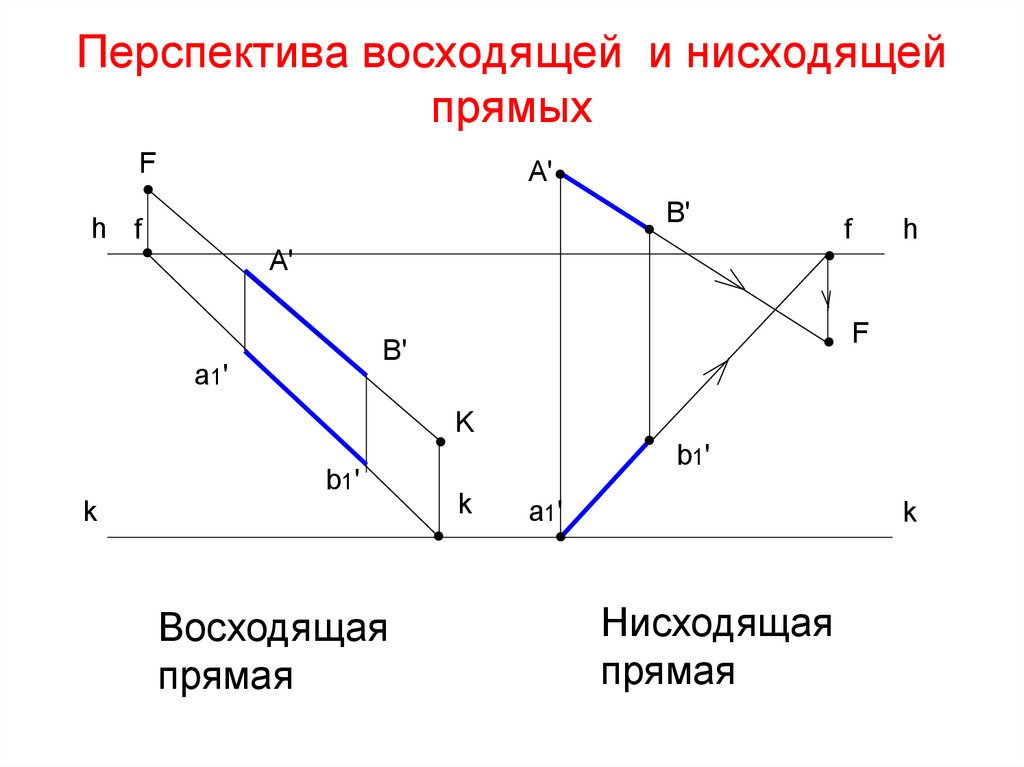
58. Перспектива восходящей и нисходящей прямых
FA'
B'
h f
f
h
A'
F
B'
a 1'
K
b 1'
k
Восходящая
прямая
b 1'
k
a1 '
k
Нисходящая
прямая
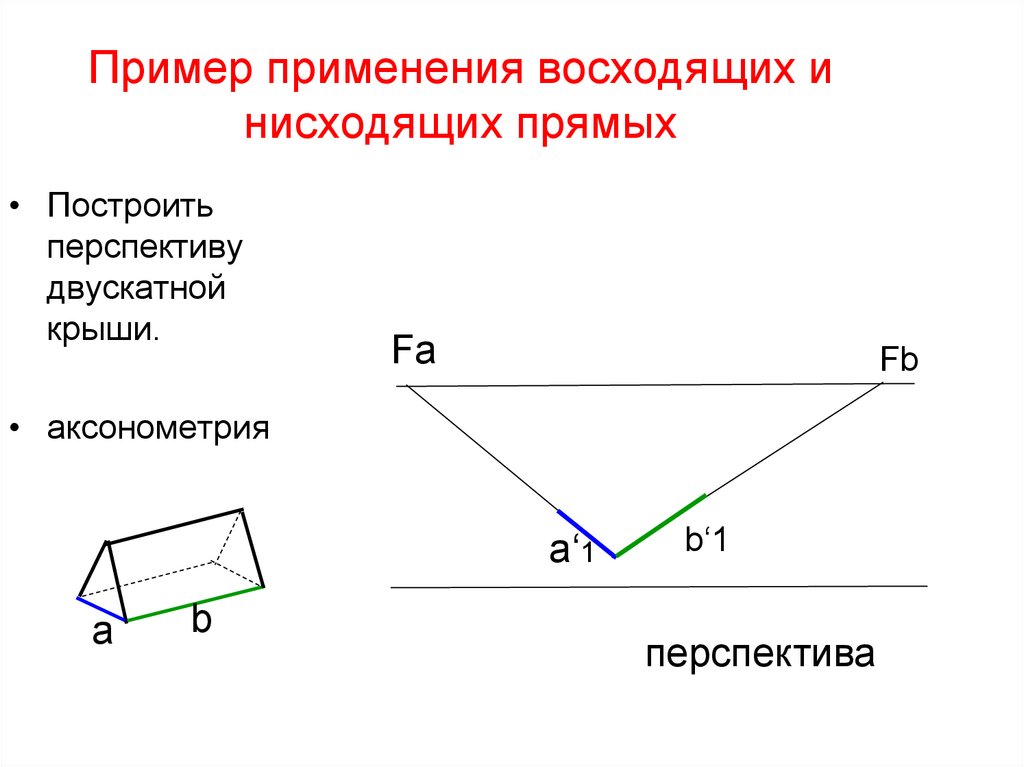
59. Пример применения восходящих и нисходящих прямых
• Построитьперспективу
двускатной
крыши.
Fa
Fb
• аксонометрия
a‘1
a
b
b‘1
перспектива
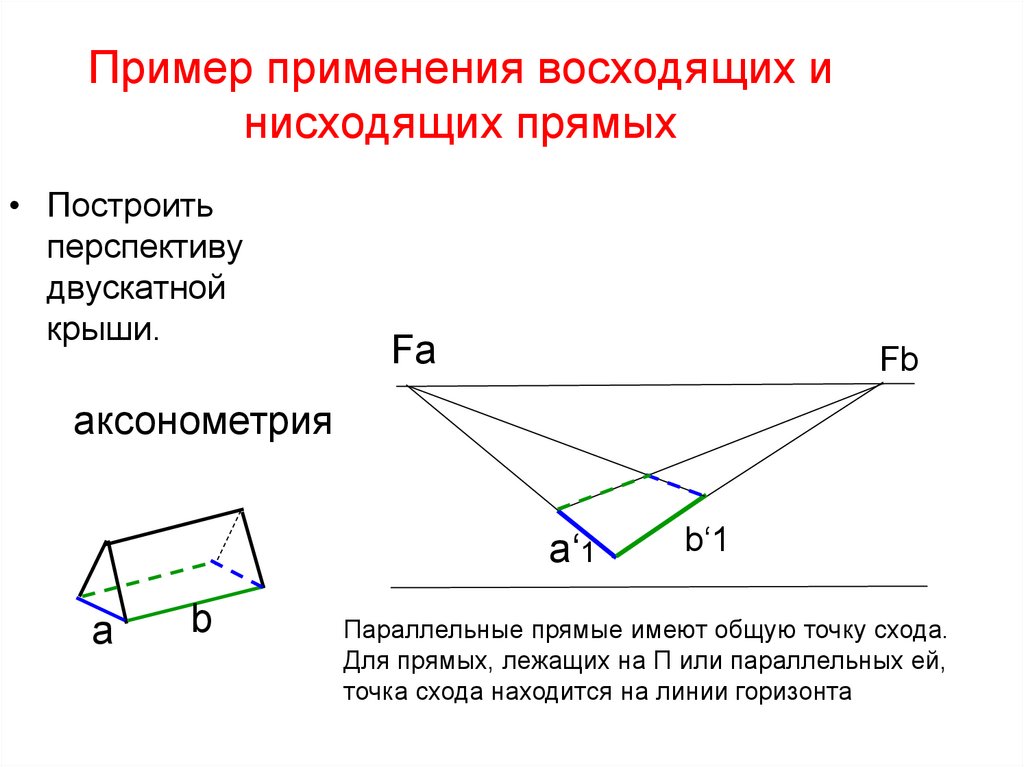
60. Пример применения восходящих и нисходящих прямых
• Построитьперспективу
двускатной
крыши.
Fa
Fb
аксонометрия
a‘1
a
b
b‘1
Параллельные прямые имеют общую точку схода.
Для прямых, лежащих на П или параллельных ей,
точка схода находится на линии горизонта
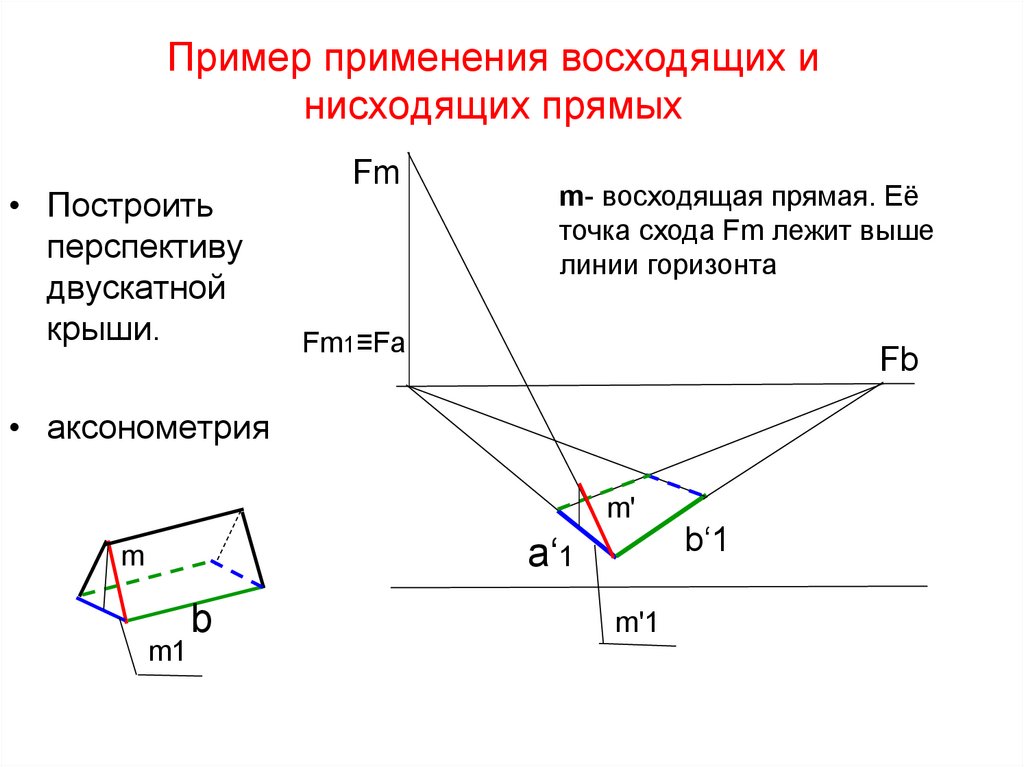
61. Пример применения восходящих и нисходящих прямых
• Построитьперспективу
двускатной
крыши.
Fm
m- восходящая прямая. Её
точка схода Fm лежит выше
линии горизонта
Fm1≡Fa
Fb
• аксонометрия
m'
b‘1
a‘1
m
m1
b
m'1
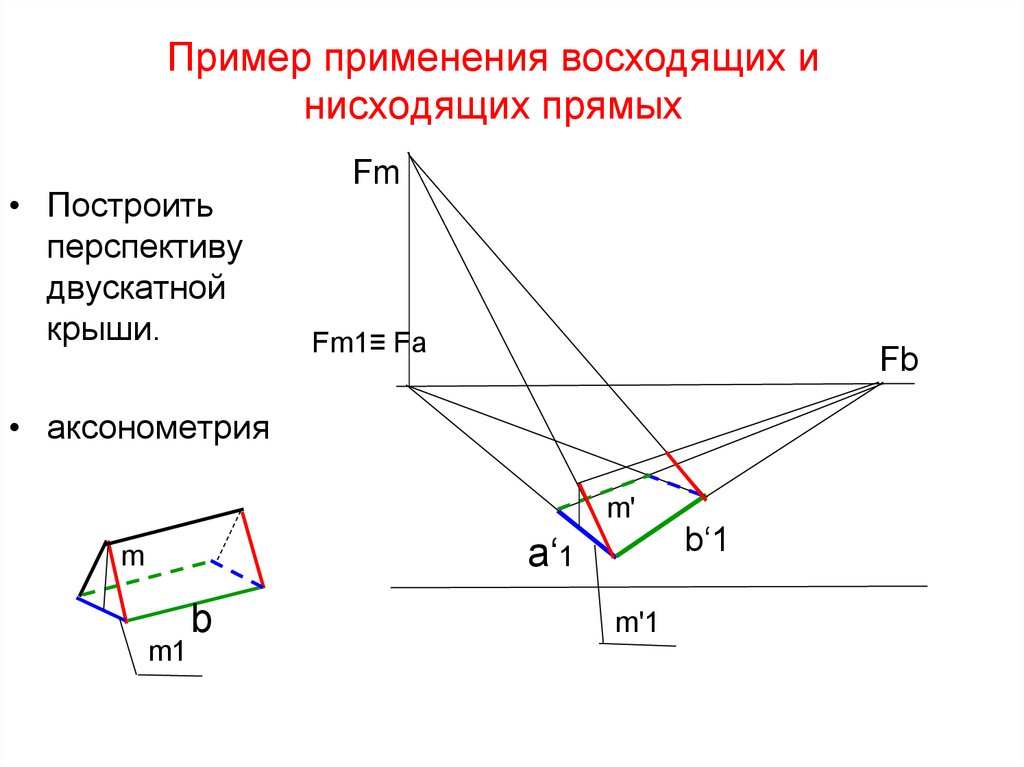
62. Пример применения восходящих и нисходящих прямых
• Построитьперспективу
двускатной
крыши.
Fm
Fm1≡ Fa
Fb
• аксонометрия
m'
b‘1
a‘1
m
m1
b
m'1
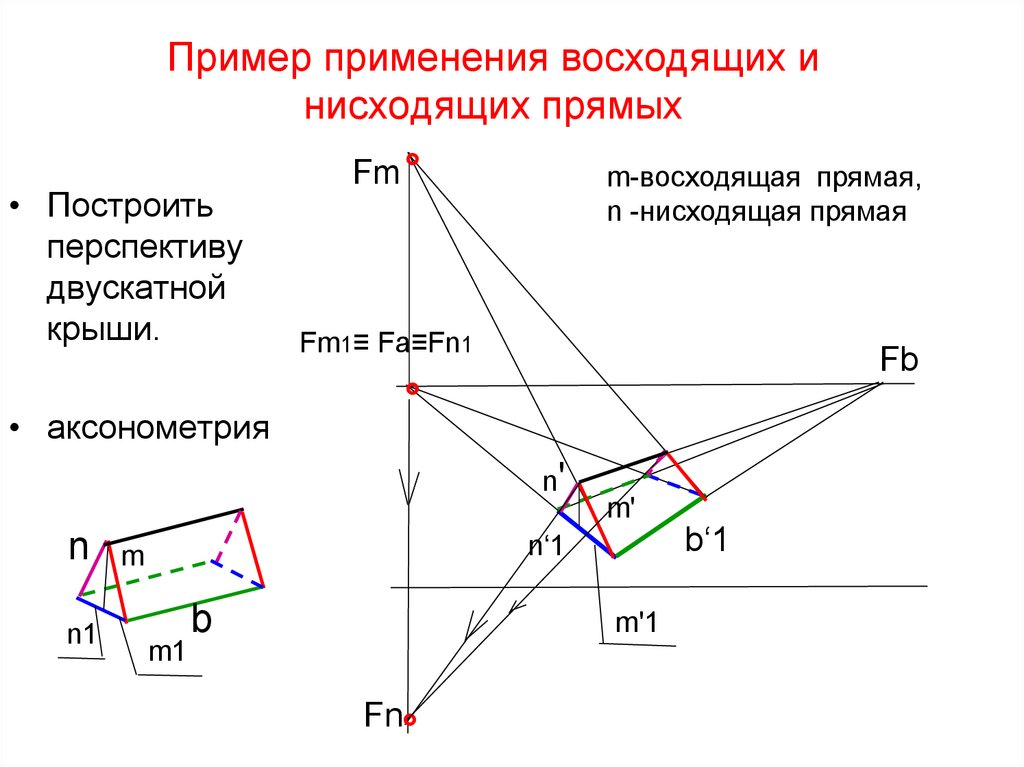
63. Пример применения восходящих и нисходящих прямых
• Построитьперспективу
двускатной
крыши.
• аксонометрия
Fm °
m-восходящая прямая,
n -нисходящая прямая
Fm1≡ Fa≡Fn1
Fb
°
n'
n
n1
m'
b‘1
n‘1
m
m1
b
m'1
Fn°
64. Перспективный эпюр
• Построить перспективу объекта можно ещеодним способом. Рассмотрим на примере
точки.
• Если провести через точку две
пересекающиеся прямые (запеленговать
точку), а потом построить перспективные
изображения этих прямых, то пересечение
перспектив данных прямых определит
перспективу данной точки.
65. Перспективный эпюр
кh
P
°
S
°
ok
h
P1
s1
п
45°
° А≡А1
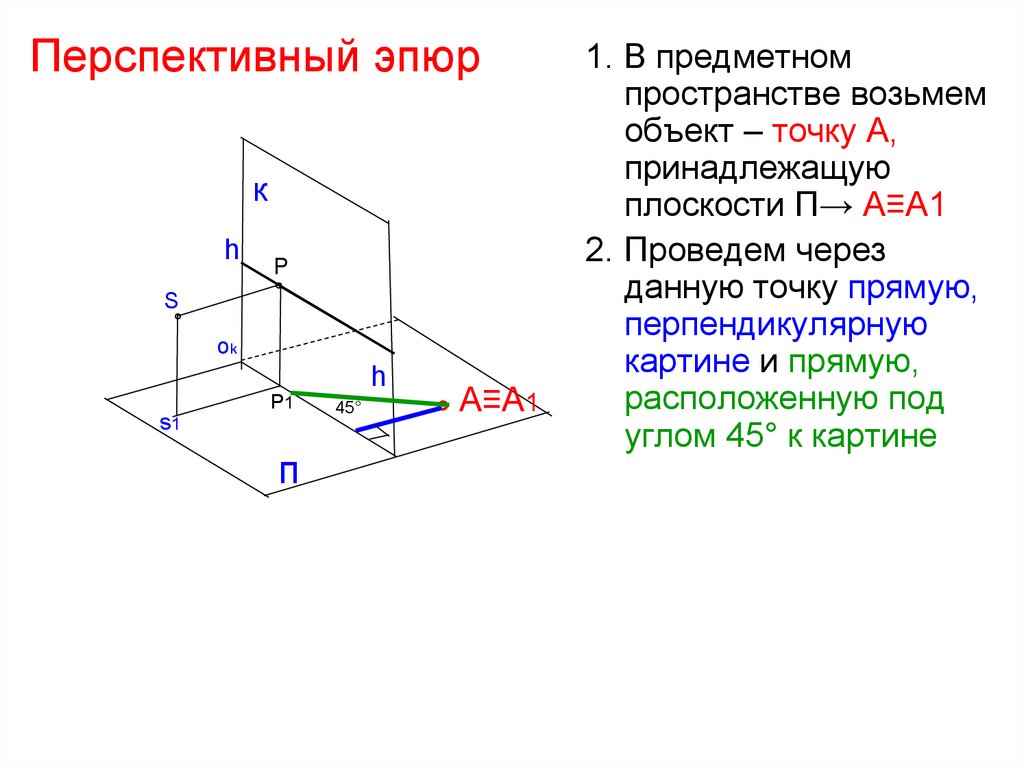
1. В предметном
пространстве возьмем
объект – точку А,
принадлежащую
плоскости П→ А≡А1
2. Проведем через
данную точку прямую,
перпендикулярную
картине и прямую,
расположенную под
углом 45° к картине
66. Перспективный эпюр
кh
P
°
S
D
°
ok
P1
s1
п
45°
h
° А≡А1
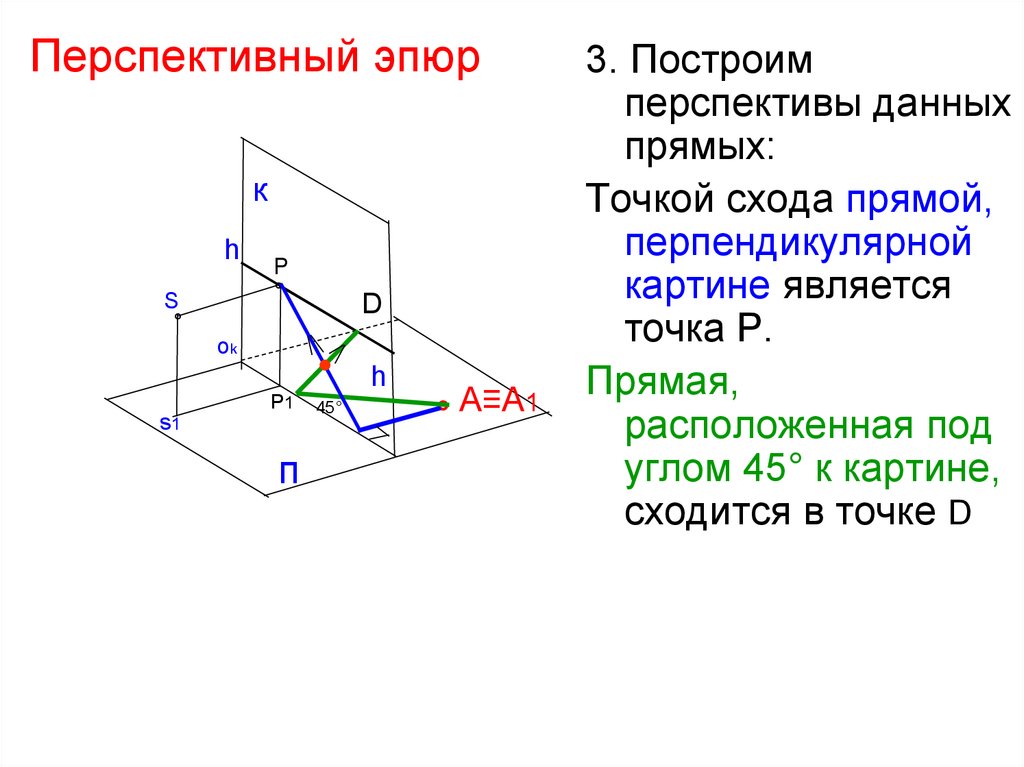
3. Построим
перспективы данных
прямых:
Точкой схода прямой,
перпендикулярной
картине является
точка Р.
Прямая,
расположенная под
углом 45° к картине,
сходится в точке D
67. Перспективный эпюр
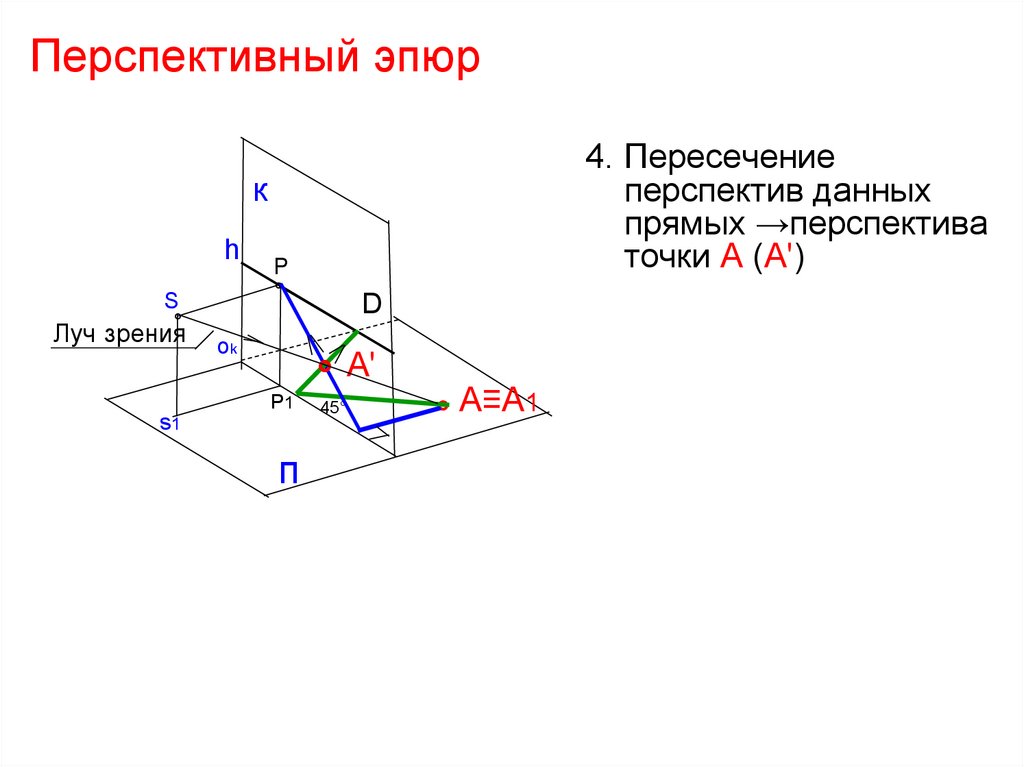
4. Пересечениеперспектив данных
прямых →перспектива
точки А (А')
к
h
P
°
S
D
°
Луч зрения
ok
P1
s1
п
° А'
45°
° А≡А1
68. Перспективный эпюр
кh
P
°
S
D
°
Луч зрения
ok
P1
s1
° А'
45°
45°
п
° А≡А1
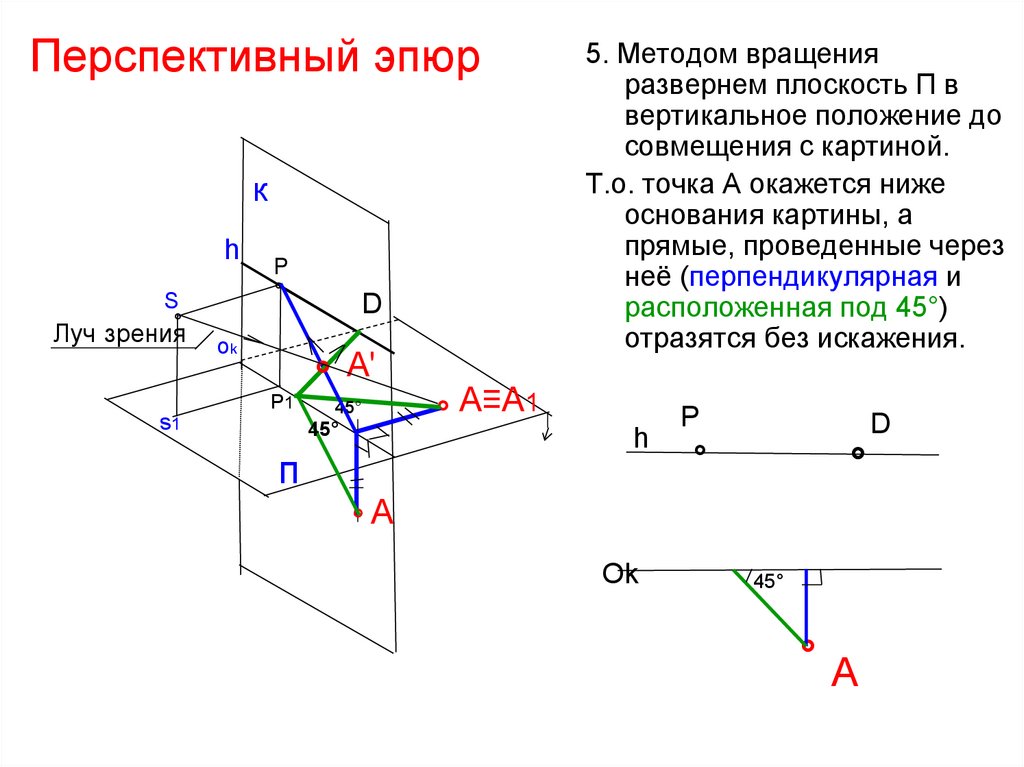
5. Методом вращения
развернем плоскость П в
вертикальное положение до
совмещения с картиной.
Т.о. точка А окажется ниже
основания картины, а
прямые, проведенные через
неё (перпендикулярная и
расположенная под 45°)
отразятся без искажения.
h
P
D
°
°
°А
Ok
45°
°A
69. Перспективный эпюр
кh
P
°
S
D
°
Луч зрения
ok
P1
s1
п
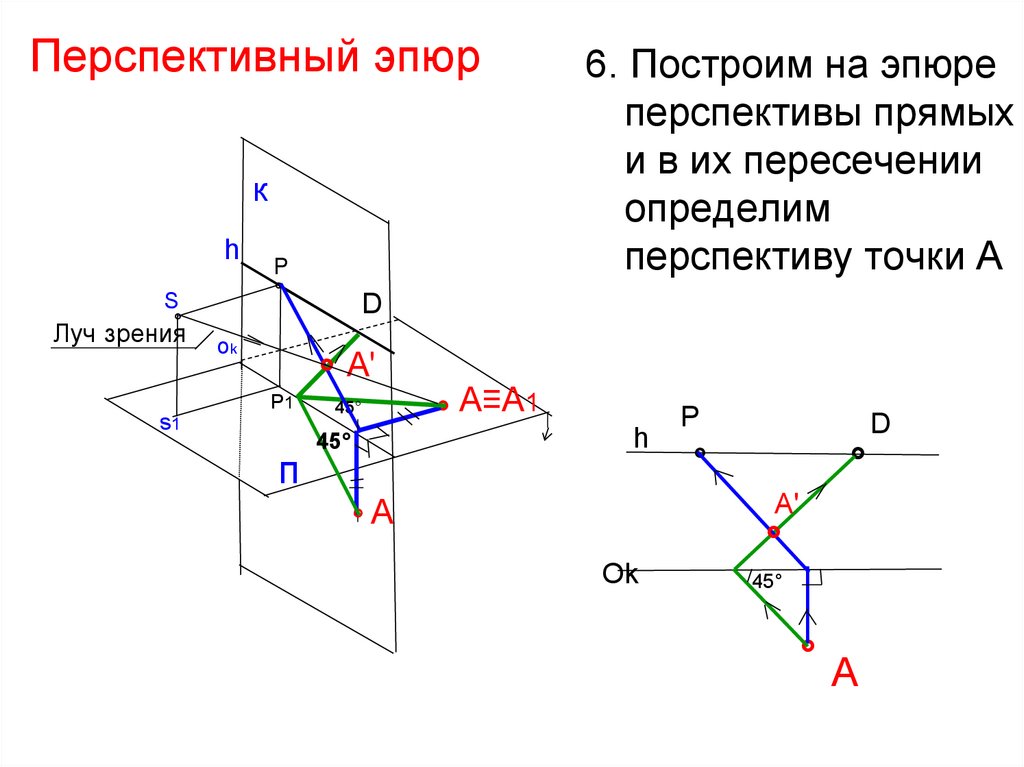
6. Построим на эпюре
перспективы прямых
и в их пересечении
определим
перспективу точки А
° А'
45°
45°
° А≡А1
h
P
D
°
°
А'
°А
Ok
°
45°
°A
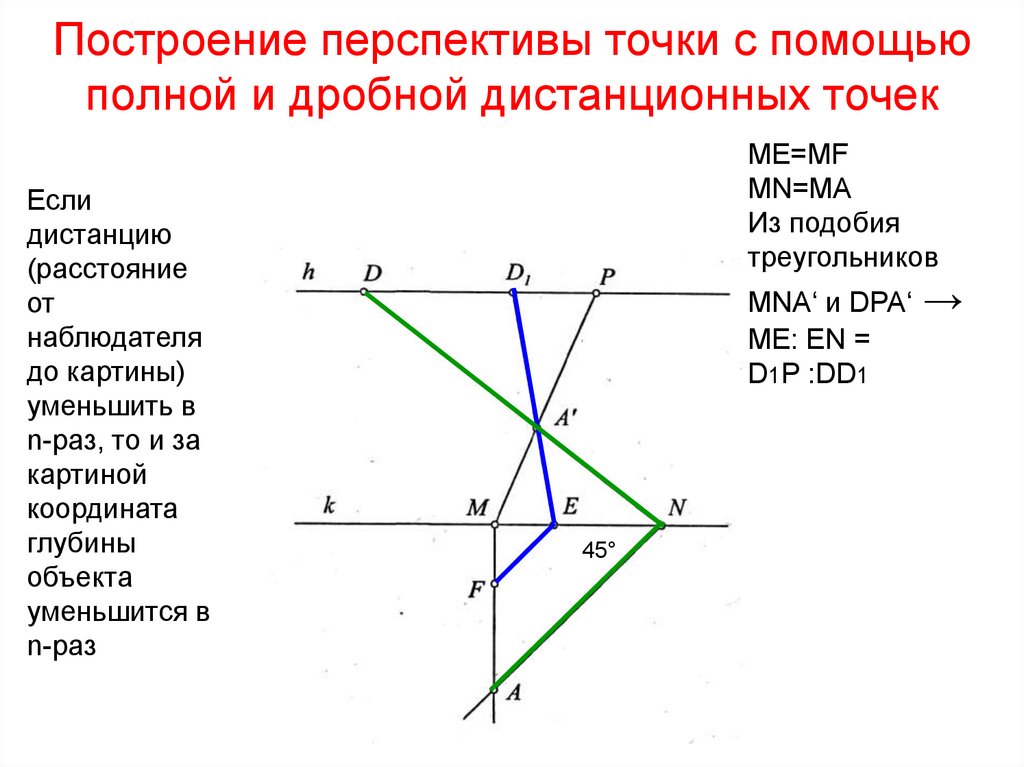
70. Построение перспективы точки с помощью полной и дробной дистанционных точек
Еслидистанцию
(расстояние
от
наблюдателя
до картины)
уменьшить в
n-раз, то и за
картиной
координата
глубины
объекта
уменьшится в
n-раз
МЕ=МF
МN=МA
Из подобия
треугольников
МNA‘ и DPA‘
ME: EN =
D1P :DD1
45°
→
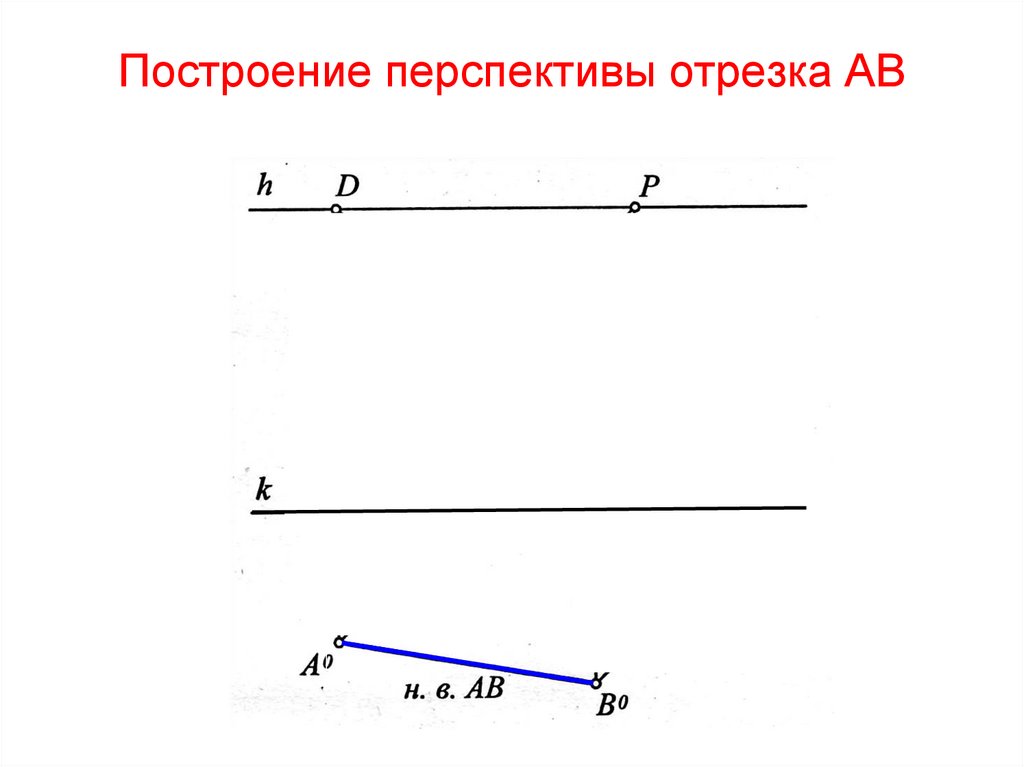
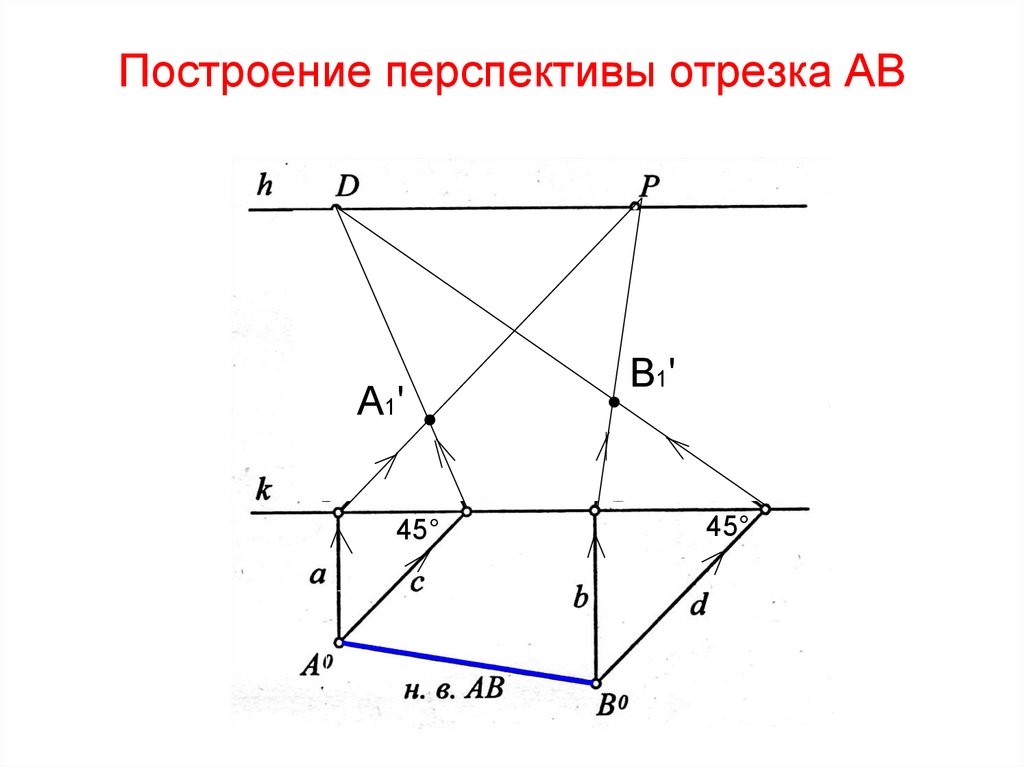
71. Построение перспективы отрезка АВ
11
45°
45°
72. Построение перспективы отрезка АВ
11
45°
45°
73. Построение перспективы отрезка АВ
A1'1
1
45°
45°
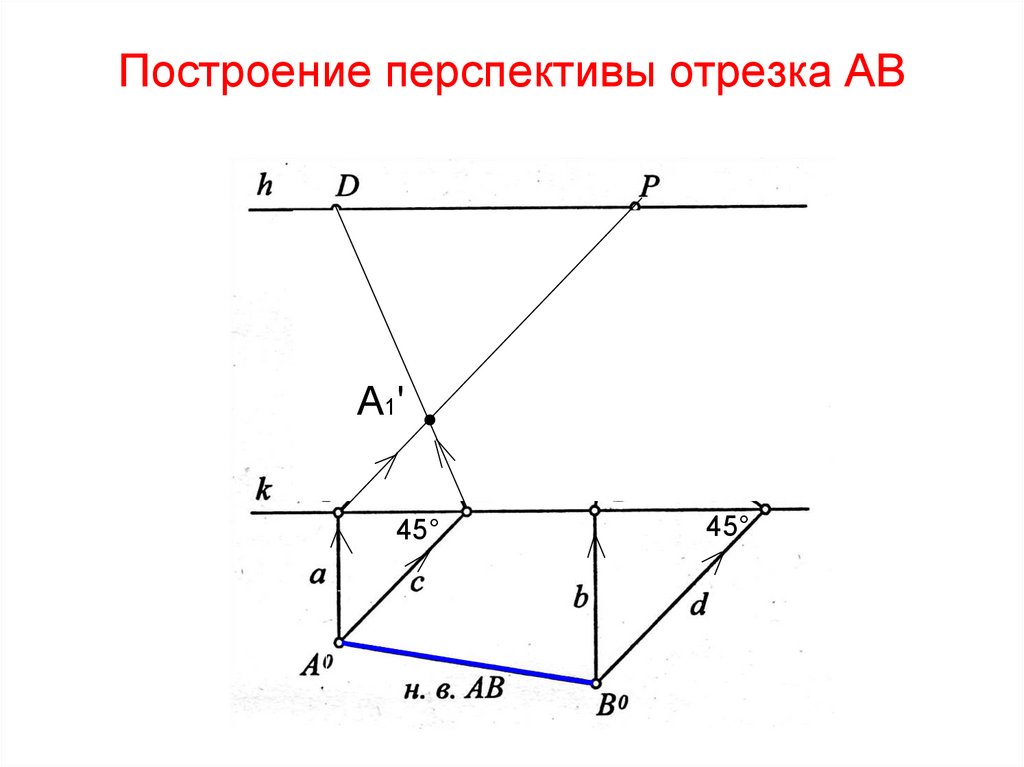
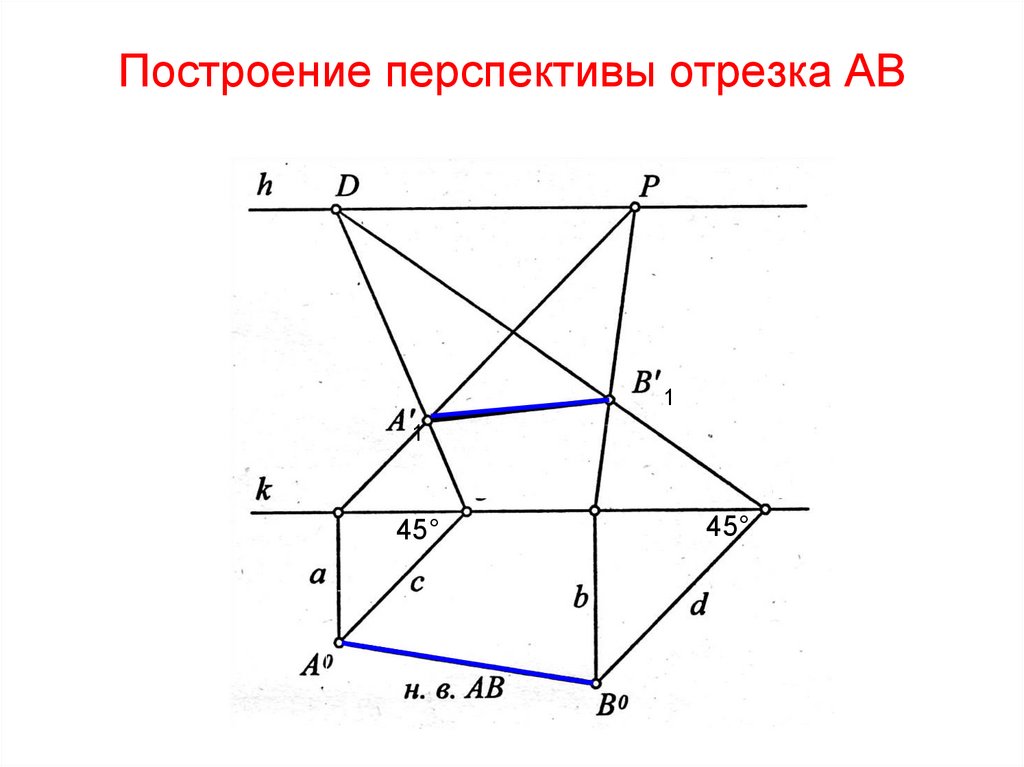
74. Построение перспективы отрезка АВ
A1'B11'
1
45°
45°
75. Построение перспективы отрезка АВ
11
45°
45°





















 Инженерная графика
Инженерная графика








