Математический аппарат для проектирования компьютерных сетей. Нахождение кратчайшего пути от одной из вершин графа до остальных

1. МДК.01.02 Математический аппарат для проектирования компьютерных сетей

ПРАКТИЧЕСКАЯ РАБОТА 0 5

2.

Практическая работа № 5
для студентов специальности 09.02.02
«Компьютерные сети»
Тема: Нахождение кратчайшего пути от одной из вершин
графа до всех остальных.
Цель работы: Приобрести навыки нахождения кратчайшего
пути от одной из вершин графа до всех остальных.
Норма времени: 2 часа.
После выполненных работ студент должен знать: определение
маршрута, пути, цикла; алгоритм Дийкстры нахождения
кратчайшего пути от одной из вершин графа до всех
остальных;
уметь: применять алгоритм Дийкстры для нахождения
кратчайшего пути.

3.

Практическая работа № 5
Теоретические сведения
Алгоритм Дийкстры находит кратчайший путь от одной
из вершин графа до всех остальных.
Алгоритм работает только для графов без рёбер
отрицательного веса.
Алгоритм основан на приписывании вершинам vi временных
меток d(vi). Метка вершины дает верхнюю границу длины пути
от s к этой вершине.
Величины меток постепенно уменьшаются, и на каждом шаге
итерации одна из временных меток становится постоянной. Это
означает, что метка дает точную длину кратчайшего пути от s к
рассматриваемой вершине.

4.

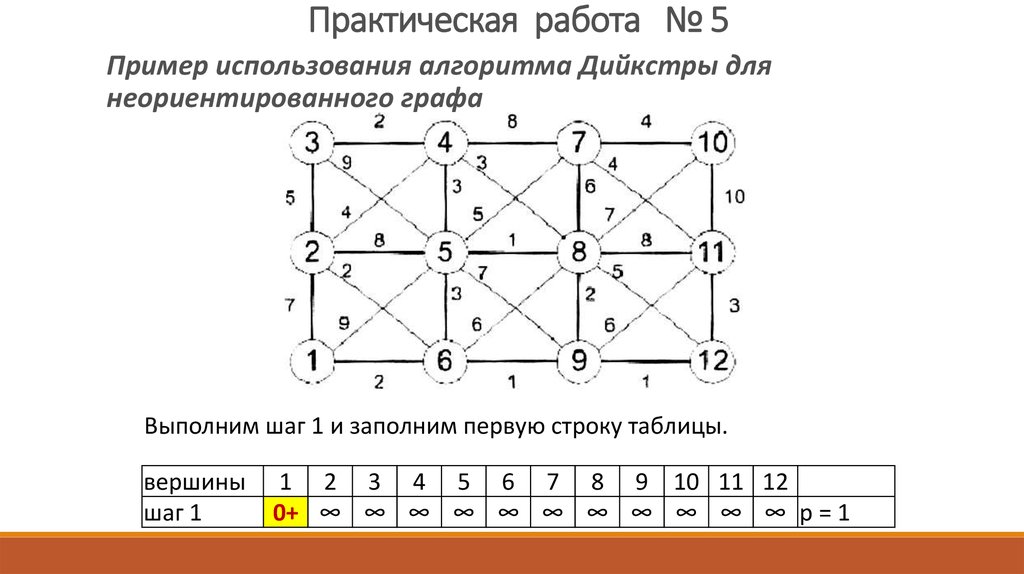
Практическая работа № 5
Шаг 1 (начальная установка).
Согласно алгоритму Дейкстры процесс построения дерева
начинается с заданной вершины.
Положить d(s)=0, считать метку постоянной.
d(vi)=∞, i=1...n, считать метки временными.
p=s.

5.

Практическая работа № 5
Шаг 2 (общий шаг).
В дальнейшем на каждом шаге к дереву присоединяется одно
новое ребро (и одна вершина).
Это ребро выбирается из подходящих ребер, причем
подходящим считается ребро, соединяющее вершину дерева с
вершиной, ему не принадлежащей (иначе образуется цикл).
Среди подходящих ребер выбирается ребро наименьшего
веса.

6.

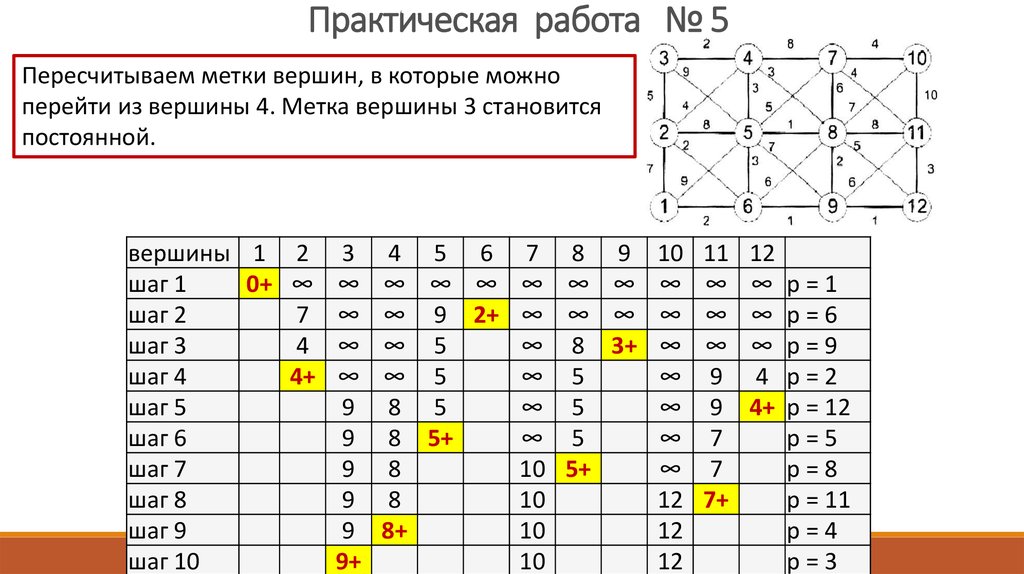
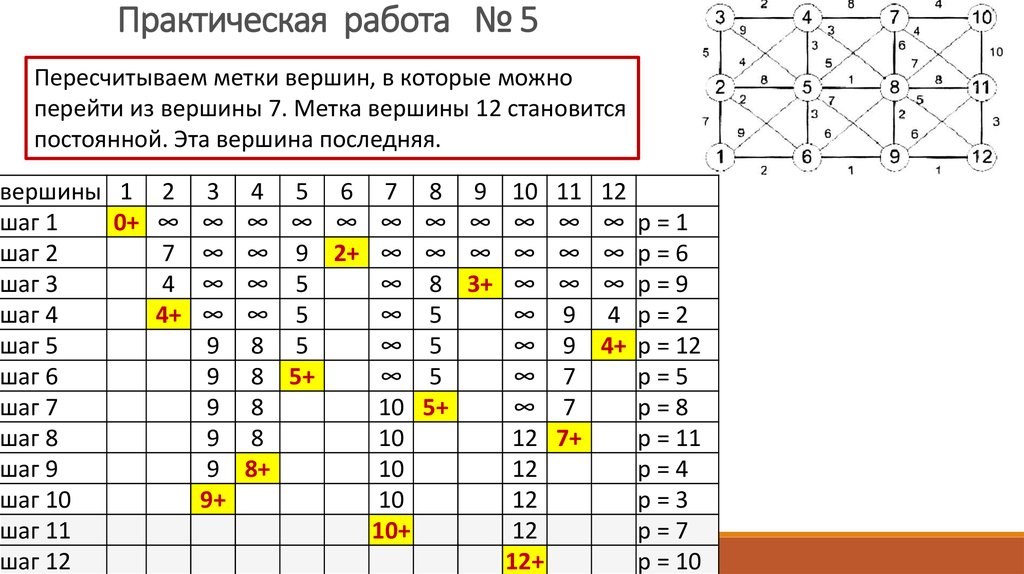
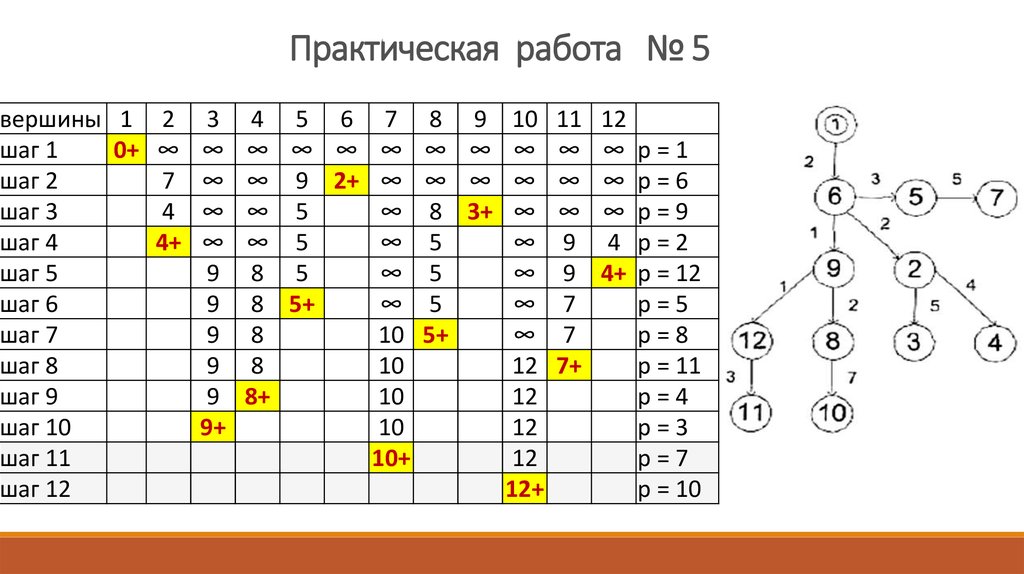
Практическая работа № 5
Повторяется n раз, пока не будут упорядочены все вершины.
Пересчитать временную метку d(vi) всякой неупорядоченной
вершины vi, в которую входит дуга, выходящая из р: