Компьютерная технология. Наблюдение

1. Компьютерная технология НАБЛЮДЕНИЕ

Моделирование
Управление
Наблюдение
Фильтрация
Идентификация
Диагностика
Адаптация
Оптимизация
Визуализация

2.

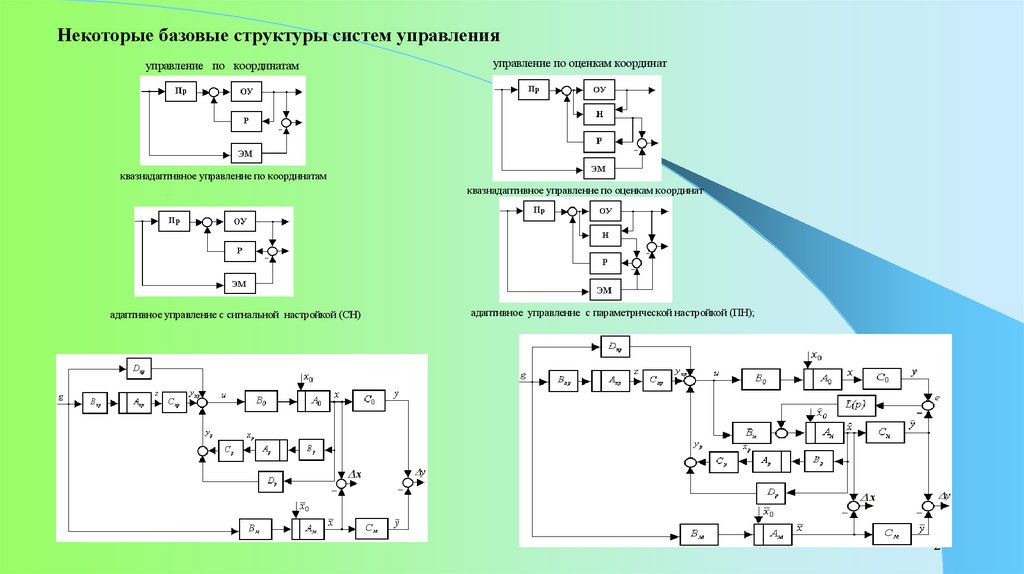
Некоторые базовые структуры систем управления
управление по координатам
управление по оценкам координат
квазиадаптивное управление по координатам
квазиадаптивное управление по оценкам координат
адаптивное управление с сигнальной настройкой (СН)
адаптивное управление с параметрической настройкой (ПН);
2

3.

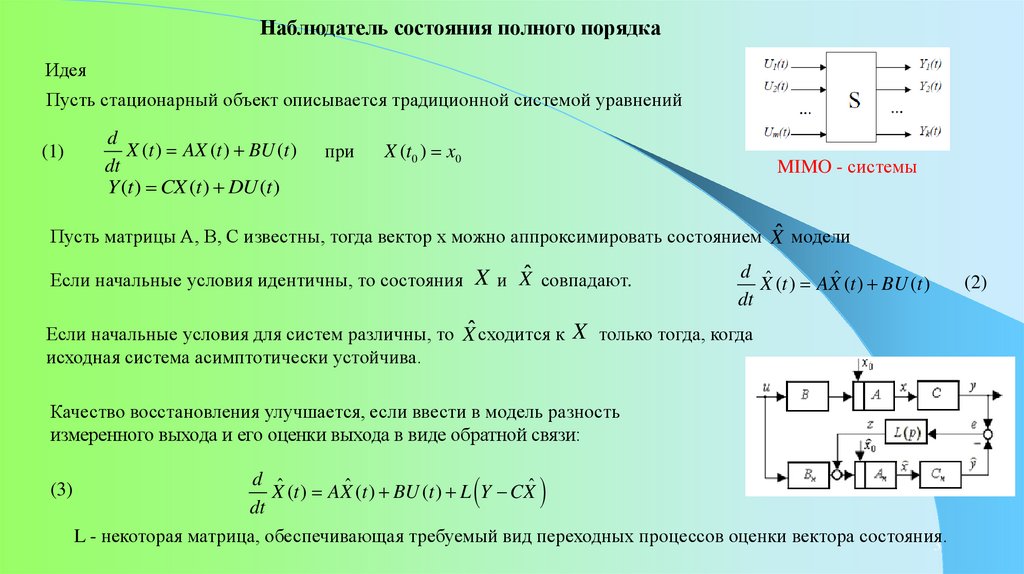
Наблюдатель состояния полного порядка
Идея
Пусть стационарный объект описывается традиционной системой уравнений
(1)
d
X (t ) AX (t ) BU (t )
dt
Y (t ) CX (t ) DU (t )
при
X (t0 ) x0
MIMO - системы
Пусть матрицы A, B, C известны, тогда вектор x можно аппроксимировать состоянием X̂ модели
Если начальные условия идентичны, то состояния X и X̂ совпадают.
d ˆ
X (t ) AXˆ (t ) BU (t )
dt
Если начальные условия для систем различны, то X̂ сходится к X только тогда, когда
исходная система асимптотически устойчива.
Качество восстановления улучшается, если ввести в модель разность
измеренного выхода и его оценки выхода в виде обратной связи:
(3)
d ˆ
X (t ) AXˆ (t ) BU (t ) L Y CXˆ
dt
L - некоторая матрица, обеспечивающая требуемый вид переходных процессов оценки вектора состояния.
3
(2)

4.

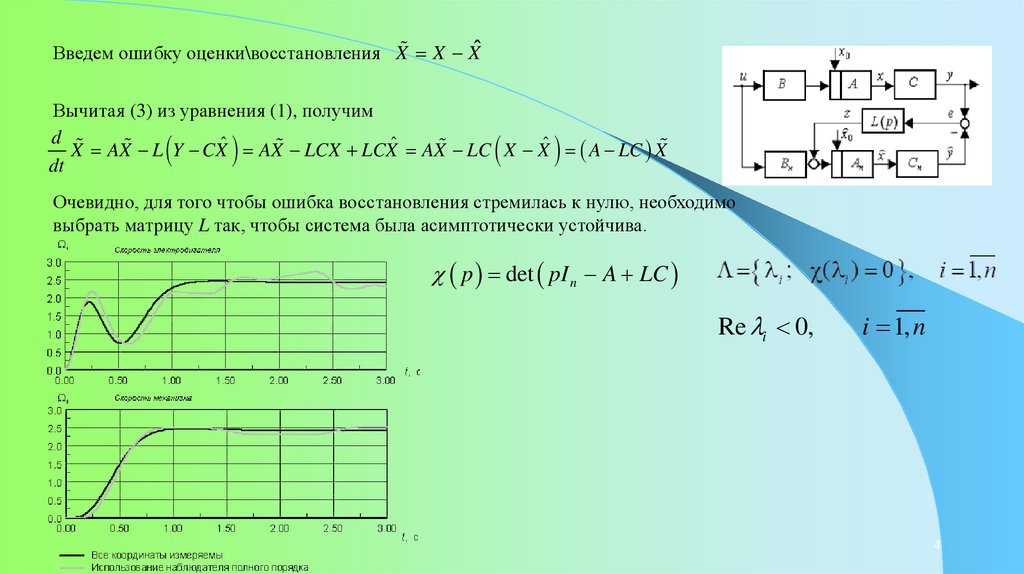
Введем ошибку оценки\восстановления X X Xˆ
Вычитая (3) из уравнения (1), получим
d
X AX L Y CXˆ AX LCX LCXˆ AX LC X Xˆ A LC X
dt
Очевидно, для того чтобы ошибка восстановления стремилась к нулю, необходимо
выбрать матрицу L так, чтобы система была асимптотически устойчива.
p det pI n A LC
Re i 0,
i 1, n
4

5.

Наблюдатель нагрузки
электромеханической
системы (пример)
Рассматривается электромеханическая система с
электродвигателем постоянного тока с
независимым возбуждением.
Ставится задача определения (оценки)
механической нагрузки ЭМС,
приведенной к ротору
электродвигателя
(1)
R
k k
k k
M m я M m m l m l u
Lя
Lя
Lя
d d
1
1 2
(M m M c )
J1 J 2
J1 J 2
M m km I я

6.

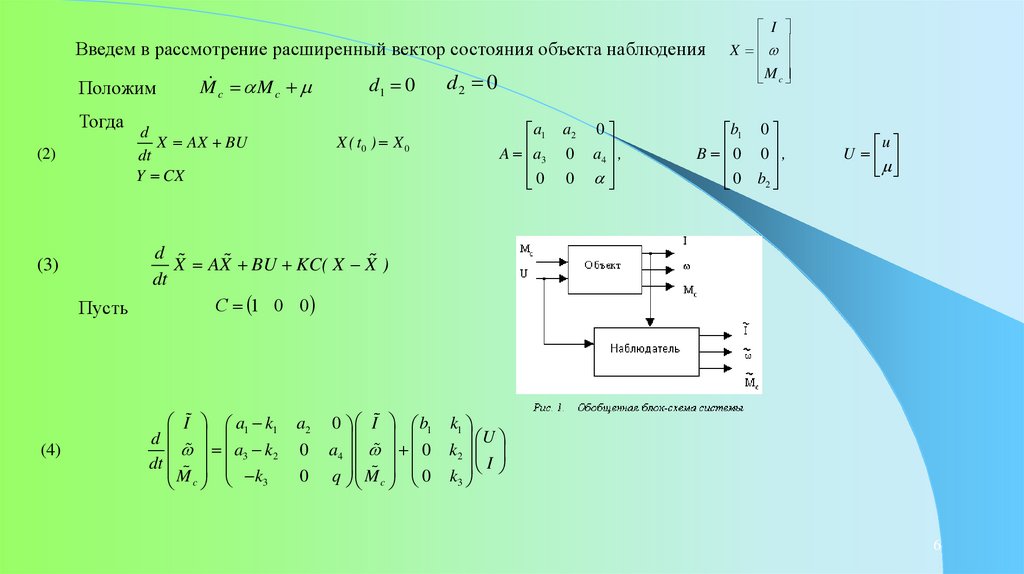
Введем в рассмотрение расширенный вектор состояния объекта наблюдения
Mc Mc
Положим
Тогда d
(2)
X ( t0 ) X 0
dt
Y CX
(3)
Пусть
(4)
X AX BU
d1 0
d2 0
a1
A a3
0
a2
0
0
0
a4 ,
I
X
M c
b1 0
B 0 0 ,
0 b2
u
U
d
X AX BU KC( X X )
dt
C 1 0 0
I a1 k1
d
a3 k2
dt
M c k3
a2
0
0
0 I b1
a4 0
q M c 0
k1
U
k2
I
k3
6

7.

Уравнения всей динамической системы в пространстве состояний
(5)
I a1
a3
d Mc 0
dt I k1
k2
M
c k3
a2
0
0
0
0
a4
0
0
0
0
0
0
0
a1 k1
a2
0
0
a3 k2
0
0
0
k3
0
0 0 0 1 0 0
Y 0 0 0 0 1 0
0 0 0 0 0 1
I
Mc
0 I b1
0 0
0 Mc 0
0 I b1
a4 0
q M c 0
I
Mc
0
0
1 U
0 Mc
0
0
T
Матричную передаточную функцию Ф( p) C p E A B
представить в виде
1
....
...
Ф( p ) ...
...
0 Ф ( p )
32
(6)
динамической системы (5) можно
Ф32 ( p )
a2 a4 k3
( p ) Z( p )
и представляет собой передаточную функцию всей обобщенной динамической системы по каналу
~
Mc Mc
Z( p ) p 3 ( q a1 k1 ) p 2 ( a2 a3 a2 k2 k1q a1q ) p a2 a4 k3 a2a3q a2k 2q
7

8.

Из модели (2) следует, что подсистема "объект" по сигналу M c является статической и ее поведение
1
описывается в (6) составляющей
p
Подсистема "наблюдатель", описываемая оставшейся частью (6), будет астатической в случае, если принять q 0
В этом случае передаточная функция канала M c M c подсистемы "наблюдатель" принимает вид
н
WMM
( p)
a2 a4 k3
p 3 ( a1 k1 ) p 2 ( a2 a3 a2 k2 ) p a2 a4 k3
Передаточная функция по ошибке в этом случае имеет вид
p( p 2 ( a1 k1 )p ( a2 a3 a2k2 ))
W ( p ) 1 W ( p ) 3
p ( a1 k1 )p 2 ( a2 a3 a2 k2 )p a2a4k3
~
Отсюда - коэффициент ошибки С0 , вычисляемый для канала M c M c равен нулю, т.е. этот канал подсистемы
становится астатическим.
н
MM
Характеристический полином наблюдателя приобретает следующий вид
Z ( p) p 3 ( a1 k1 ) p 2 ( a 2 a 3 a 2 k 2 ) p a 2 a 4 k 3
8

9.

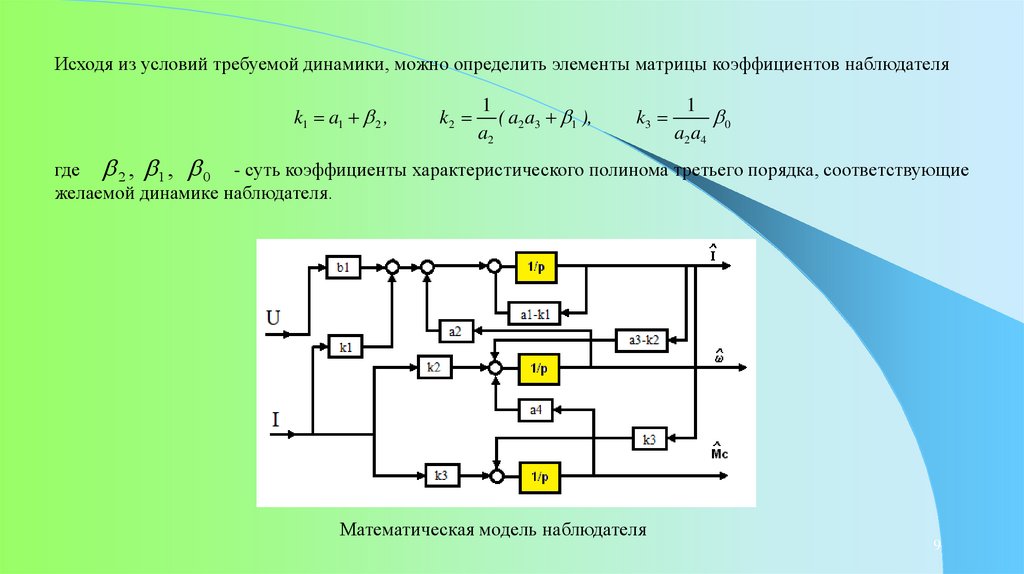
Исходя из условий требуемой динамики, можно определить элементы матрицы коэффициентов наблюдателя
k1 a1 2 ,
k2
1
( a2 a3 1 ),
a2
k3
1
0
a2 a4
где 2 , 1 , 0 - суть коэффициенты характеристического полинома третьего порядка, соответствующие
желаемой динамике наблюдателя.
Математическая модель наблюдателя
9

10.

При непосредственном измерении угловой скорости матрица С имеет вид
C 0 1 0
В этом случае математическая модель наблюдателя (3) приобретает вид:
I a1
d
a3
dt
Mc 0
a2 k1
k2
k3
0 I b1 k1
U
a4 0 k2
q M c 0 k3
В этого варианта настроечные коэффициенты наблюдателя имеют вид
(16)
k3
1
0 ,
a1a4
k 2 a1 2 ,
k1 ( 1 a2 a3 a1k 2 a4 k 3 ) / a3
1 0 0
0
При использовании измеренных значений тока статора и угловой скорости, т.е. при C
0 1
I a1 k11
d
a3 k21
dt
M c k31
a2 k12
k22
k32
0 I b1
a4 0
q M c 0
k11
k21
k31
k12 U
k22 I
k32

11.

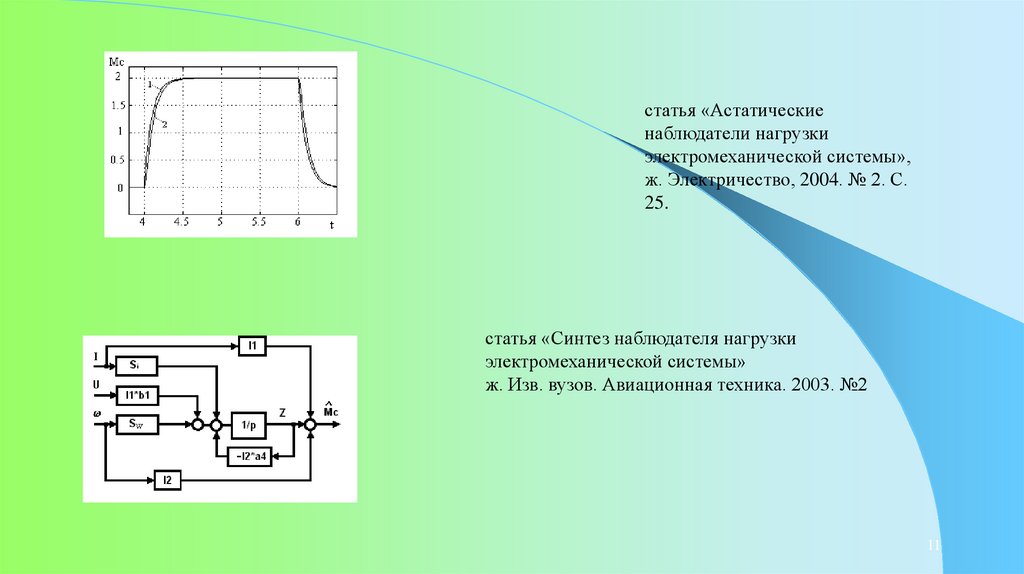
статья «Астатические
наблюдатели нагрузки
электромеханической системы»,
ж. Электричество, 2004. № 2. С.
25.
статья «Синтез наблюдателя нагрузки
электромеханической системы»
ж. Изв. вузов. Авиационная техника. 2003. №2
11

12.

Дополнительная литература
1. Андреев Ю.Н. Управление линейными конечномерными объектами. // М.: Наука.
Физматлит. 1976.
2. Коровин С.К., Фомичев В.В. Наблюдатели состояния для линейных систем с
неопределенностью. Москва. Физматлит. 2007. 223 с.
3. O'Reilly J. Observers for linear systems. // Academic Press. London. 1983.
12

13.

13

14.

14

15.

15