Похожие презентации:
Прямая и плоскость. Лекция 5
1. Прямая и плоскость
Лекция 52. 2. Плоскость
1) Общее уравнение плоскости (рис.14)Ax By Cz D 0 ,
если A 2 B 2 C 2 0 ,
где n A, B, C - нормальный вектор плоскости p , n p ;
n
Рисунок 14
2) Уравнение плоскости, проходящей через точку M 0 (x 0 , y 0 , z 0 ) и
перпендикулярной вектору n A, B, C
A x x0 B y y0 C z z 0 0 ;
3.
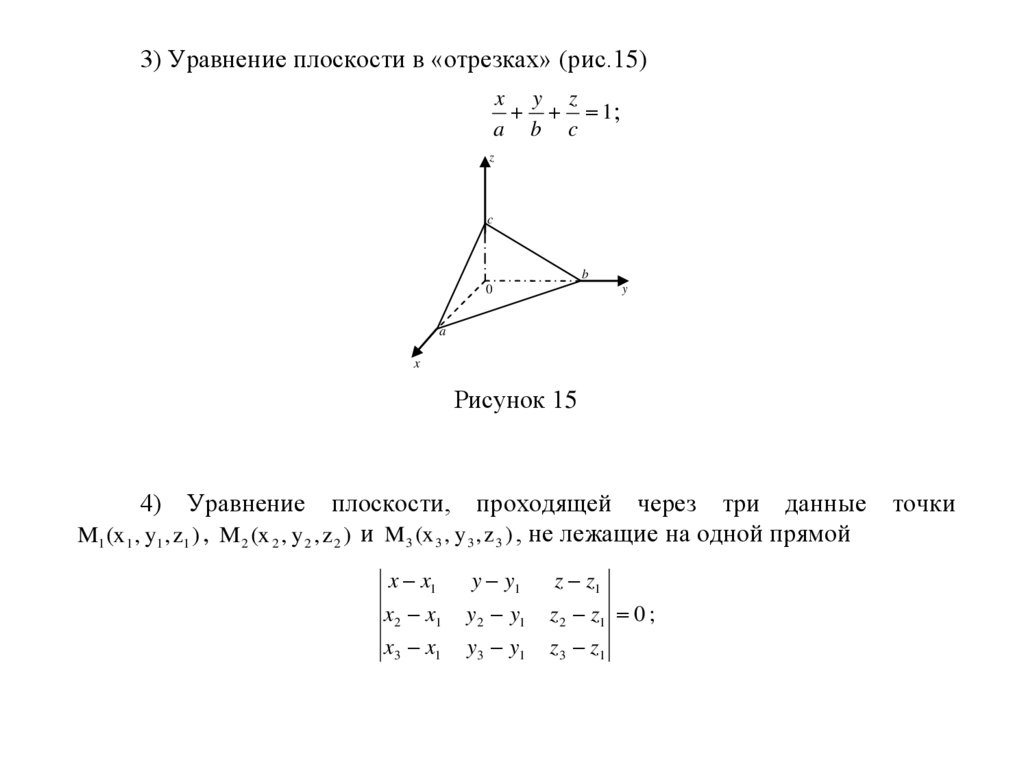
3) Уравнение плоскости в «отрезках» (рис.15)x y z
1;
a b c
z
c
b
y
0
a
x
Рисунок 15
4) Уравнение плоскости, проходящей через три данные
M1 (x 1 , y1 , z1 ) , M 2 (x 2 , y 2 , z 2 ) и M 3 (x 3 , y 3 , z 3 ) , не лежащие на одной прямой
x x1
x 2 x1
x3 x1
y y1
y 2 y1
y3 y1
z z1
z 2 z1 0 ;
z 3 z1
точки
4.
5) Угол между плоскостямиA1 x B1 y C1 z D1 0 и A2 x B2 y C2 z D2 0
определяется по формуле
cos
A1 A2 B1 B2 C1C 2
A B C A B C
2
1
2
1
Условие параллельности плоскостей:
2
1
2
2
2
2
2
2
.
A1 B1 C1
;
A2 B2 C 2
Условие перпендикулярности плоскостей: A1 A2 B1 B2 C1C2 0 ;
6) Расстояние d от точки M 0 (x 0 , y 0 , z 0 ) до плоскости Ax By Cz D 0
находится по формуле
d
Ax0 By 0 Cz0 D
A B C
2
2
2
.
5. 3. Прямая в пространстве
1) Общее уравнение прямой в пространстве (прямая как линияпересечения двух плоскостей)
A1 x B1 y C1 z D1 0
A2 x B2 y C 2 z D2 0
2)
Канонические уравнения прямой, проходящей через точку
M 0 (x 0 , y 0 , z 0 ) параллельно вектору a l , m, n ( a - направляющий вектор
прямой):
x x0 y y 0 z z 0
;
l
m
n
3) Параметрические уравнения можно получить из канонических
уравнений, введя параметр t :
x x0 l t ,
y y0 m t ,
z z n t
0
( t );
4) Уравнение прямой, проходящей через две точки M1 (x1 , y1 , z1 ) и
M 2 (x 2 , y 2 , z 2 ) :
x x1
y y1
z z1
;
x 2 x1 y 2 y1 z 2 z1
6.
5) Угол между прямымиx x1 y y1 z z1
l1
m1
n1
и
x x2 y y 2 z z 2
l2
m2
n2
определяется по формуле
cos
l1l 2 m1 m2 n1 n2
l m n l m n
2
1
Условие параллельности прямых:
2
1
2
1
2
2
2
2
2
2
.
l1 m1 n1
;
l 2 m2 n 2
Условие перпендикулярности прямых: l1l2 m1m2 n1n2 0 .
6)
Угол
между
x x0 y y 0 z z 0
l
m
n
прямой
Ax By Cz D 0 находится по формуле:
sin
Al B m C n
A B C l m n
2
2
2
2
2
2
.
Условие параллельности прямой и плоскости: A l B m C n 0 ;
Условие перпендикулярности прямой и плоскости:
A B C
.
l m n
и
плоскостью
7. 4 Полярные координаты
Положение некоторой точки M на плоскости определяется ее расстояниемOM от полюса O и углом , образованным отрезком OM с полярной осью
Ou (рис.16), при этом называется полярным радиусом точки, - ее
полярным углом ( 0 , 0 2 ).
M
ρ
φ
O
U
Рисунок 16
Если начало декартовой прямоугольной системы координат совместить с
полюсом, а ось Ox направить по полярной оси, то прямоугольные координаты
x и y точки M и ее полярные координаты и связаны формулами:
x cos ,
y sin
т.е. cos
x
x y
2
2
,
sin
и обратно,
y
x y2
2
.
x 2 y 2 ,
y
tg
x
8.
Пример. Даны точки A1 3, 5, 4 , A2 8, 7, 4 , A3 5,10, 4 , A4 4, 7, 8 .Составить уравнения:
а) плоскости A1 A2 A3 ;
б) прямой A1 A2 ;
в) прямой A4 M , перпендикулярной к плоскости A1 A2 A3 ;
г) прямой A3 N , параллельной прямой A1 A2 ;
д) плоскости, проходящей через точку A4 перпендикулярно к прямой A1 A2 .
Найти:
е) синус угла между прямой A1 A4 и плоскостью A1 A2 A3 ;
ж) расстояние от точки A4 до плоскости A1 A2 A3 .
Решение.
а) Используя формулу уравнения плоскости, проходящей через три точки, составим
уравнение плоскости A1 A2 A3 . Подставим координаты точек A1 3, 5, 4 , A2 8, 7, 4 ,
A3 5,10, 4 :
x 3 y 5 z 4
8 3 7 5 4 4 0
5 3 10 5 4 4
x 3 y 5 z 4
5
2
0 0
2
5
0
x 3 2 0 y 5 0 2 z 4 5 5 z 4 2 2 x 3 5 0 y 5 5 0 0 ;
0 0 25z 100 4z 16 0 0 0 ; 21z 84 0 .
Разделим обе части уравнения на 4, уравнение плоскости A1 A2 A3 имеет вид: z 4 0 .
9.
б) Зная координаты A1 3, 5, 4 и A2 8, 7, 4 , составим уравнение прямой A1 A2 :x 3 y 5 z 4
.
8 3 7 5 4 4
x 3 y 5 z 4
Получаем уравнение прямой A1 A2 :
.
5
2
0
в) Так как прямая A4 M перпендикулярна плоскости A1 A2 A3 , то в качестве
направляющего вектора прямой s можно взять нормальный вектор n 0;0;1
плоскости A1 A2 A3 . Тогда уравнение прямой A4 M запишется в виде:
x 4 y 8 z 9
.
0
0
1
г) Прямые A3 N и A1 A2 параллельны, поэтому в качестве направляющего
вектора для прямой A3 N можно использовать направляющий вектор s 5;2;0
прямой A1 A2 :
x 5 y 10 z 4
.
5
2
0
10.
д) Плоскость перпендикулярна прямой, следовательно, за нормальный векторплоскости можно принять направляющий вектор прямой A1 A2 .
Подставим координаты точки A4 4, 7, 8 и нормального вектора n 5;2;0 в общее
уравнение плоскости:
5 x 4 2 y 7 0 z 8 0 ,
5 x 20 2 y 14 0 .
Таким образом, уравнение плоскости: 5 x 2 y 34 0 .
x 3 y 5 z 4
,
1
2
4
A1 A2 A3 : z 4 0 .
е) A1 A4 :
Направляющий вектор прямой s 1;2;4 , а нормальный вектор плоскости n 0;0;1 .
sin
0 1 0 2 21 4
0 0 441 1 4 16
84
21 21
4 21
.
21
ж) Расстояние от точки A4 4, 7, 8 до плоскости z 4 0 найдем по формуле:
d
тогда d
8 1
0 0 1
7.
Ax0 By 0 Cz0 D
A B C
2
2
2
,









 Математика
Математика








