Похожие презентации:
Интегрирование классов функций
1.
§31. Интегрирование классовфункций
п.1. Интегрирование рациональных
функций.
Рациональная функция есть отношение
двух многочленов.
2.
n m R (x ) ― правильнаярациональная дробь
n m R (x ) ― неправильная
рациональная дробь
3.
Всякую неправильную рациональную дробьпутем деления можно представить в виде
суммы многочлена и правильной
рациональной дроби.
Pn ( x )
Ps ( x )
n
m
T ( x)
,
s m
Qm ( x )
Qm ( x )
4.
Простейшие рациональные дробиI.
A
,
II.
k 2
k
( x a) k N
A
x a
Mx N
,
III.
2
x px q
Mx N
,
IV.
2
k
( x px q )
p 4q 0
k 2 k N p 4q 0
2
A, M , N , a , p , q R
2
5.
Всякую правильную рациональную дробьPs ( x )
, s m,
Qm ( x )
знаменатель которой разложен на множители
Q m ( x ) ( x x1 ) ...( x xl )
kl
k1
( x p1 x q1 ) ...( x p t x q t ) ,
s1
2
D 0
st
2
D 0
можно представить (и притом единственным
образом) в виде суммы простейших дробей.
6.
Множителю вида ( x x ) соответствует1
сумма k простейших дробей
k
A3
Ak
A1
A2
...
2
3
k
x x1 ( x x1 ) ( x x1 )
( x x1 )
7.
Множителю вида ( x px q ) , p 4 q 0,соответствует сумма s простейших дробей
s
2
M sx Ns
M 1 x N1
M 2x N2
2
... 2
2
2
s
x px q ( x px q )
( x px q )
8.
Пример. Разложить в сумму простейшихдробей
3
.
2
2
( x 1)( x 2) ( x x 1)
Решение.
3
A1
2
2
( x 1)( x 2) ( x x 1) x 1
A3
A2
Mx N
x 2 ( x 2) 2 x 2 x 1
9.
3( x 1)( x 2) 2 ( x 2 x 1) dx
A3
A1
A2
Mx N
dx
dx
dx
dx
x 1
x 2
( x 2) 2
x2 x 1
A1 , A2 , A3 , M , N находятся методом
неопределенных
коэффициентов
10.
п.2. Интегрирование функций,содержащих квадратный трехчлен.
I1
I3
dx
I2
x bx c
2
Ax B
x bx c
2
dx
I4
dx
x bx c
2
Ax B
x bx c
2
dx
11.
Интегралы I1и I 2 приводятся к табличным,путем выделения полного квадрата.
Пример.
x 3 t
x 2 6 x 13 ( x 3) 2 4 dx dt
dt
1
t
1
x 3
2
arctg
C
arctg
C
2
2
2
2
2
t 2
dx
1
x
arctg
C
a2 x2 a
a
dx
dx
12.
Интегралы I 3и I 4 представляются в видесуммы
du
dx
I3
2
u
x bx c
u x bx c
2
du
dx
I4
2
u
x bx c
13.
Пример.2x 7
x 6 x 13 u
x 2 6 x 13 dx (2 x 6)dx du
2
( 2 x 6) 1
du
dx
2
dx
2
u
x 6 x 13
x 6 x 13
1
x 3
1
x 3
2
ln | u | arctg
C ln | x 6 x 13 | arctg
C
2
2
2
2
14.
Замечание. Если в рассматриваемыхинтегралах квадратный трехчлен имеет вид
ax bx c,
2
то вынося коэффициент a за скобки можно
прийти к рассмотренным случаям.
c
2 b
ax bx c a x x
a
a
2
15.
п.3. Интегрирование простейшихиррациональностей.
I1 R x , x dx
Замена:
n
x t
n
x t
n 1
dx nt dt
n
16.
Пример.33
x t
x t
2
dx
3t dt
3
1 3 x x t
1 t
2
dx 3t dt
Получили интеграл от рациональной функции.
Самостоятельно: вычислить указанный
интеграл.
17.
sk rs1 r s2 r
I 2 R x, x 1 , x 2 ,..., x k dx
m НОК s1 , s 2 ,..., s k
Замена:
x t
m 1
dx mt dt
m
18.
Пример.m
m
НОК
НОК ((22;;33))
66
x
1 3 x dx x t , dx 6t dt
6
5
x t , x t
3 3
t
3
1 t
2
5
6
t
dt
2
Получили интеграл от рациональной функции.
Самостоятельно: вычислить указанный
интеграл.
19.
r1r2
rk
sk ax b
s1 ax b s2 ax b
I 3 R x,
,
,...,
dx
cx d
cx d
cx d
m НОК s1 , s 2 ,..., s k
Замена:
ax b m
t
cx d
20.
Пример.x 1
dx
3
x 1 x 1
6
m
m
НОК
НОК((22;;33;;66))
66
66
55
xx
11
tt ,, dx
dx
66tt dt
dt
x 1 t , x 1 t
3 3
6
t
2
x 1 t
3 2 6t dt
t t
5
Получили интеграл от рациональной функции.
Самостоятельно: вычислить указанный
интеграл.
21.
п.4. Интегрирование некоторыхтригонометрических функций.
I1 R sin x , cos x dx
Универсальная
тригонометрическая
подстановка:
x
tg t
2
22.
xtg t
2
x
2 tg
2t
2
sin x
2
2 x
1 t
1 tg
2
x 2 arctg t
1 tg
2 x
1 t
2
cos x
2
2 x
1 t
1 tg
2
dx ( 2arctg t )' dt
2
2
1 t
dt
2
23.
Пример.x
tg x t
tg 2 t
dx
3 5 cos x 2 1 t 2
2dt
cos x
,
dx
2
2
1
t
1
t
2dt
2
2dt
1
t
2
2
2
1 t
3(1 t ) 5(1 t )
3 5
2
1 t
Самостоятельно: вычислить указанный
интеграл.
24.
I 2 cos x sin xdx,m, n Z
замена:
замена:
sin x t
cos x t
m
1) m ─ нечетное
2) n ─ нечетное
3) m,n ─ четные
n
1 cos 2
1 cos 2
2
cos
sin
2
2
4) m n ─ четное отрицательное
замена:
tg x t
2
25.
Пример.sin
x
cos
xdx
sin
x
cos
x
cos
xdx
2
3
2
sin x t
cos xdx dt
2
t (1 t ) dt
2
2
cos x 1 sin x
2
2
3
5
3
5
t
t
sin x sin x
t dt t dt C
C
3 5
3
5
2
4
26.
Пример.dx
cos x sin 3 x
1
cos x sin
3
xdx
tg x t , x arctg t ,
tg x t , x arctg t ,
dt
t
1
dx
,
sin
x
,
cos
x
2
2
2
1 t
1 t
1 t
2
2
3
1 t 1 t dt
1 t
dt
3
1 t 1 t2
t
2












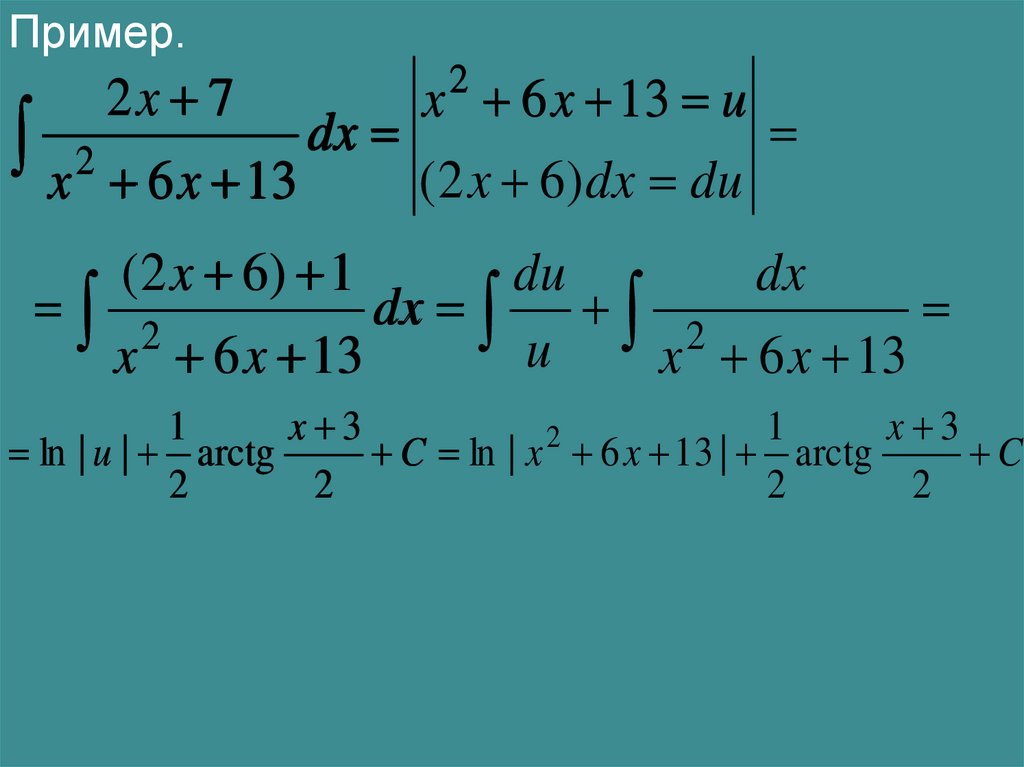








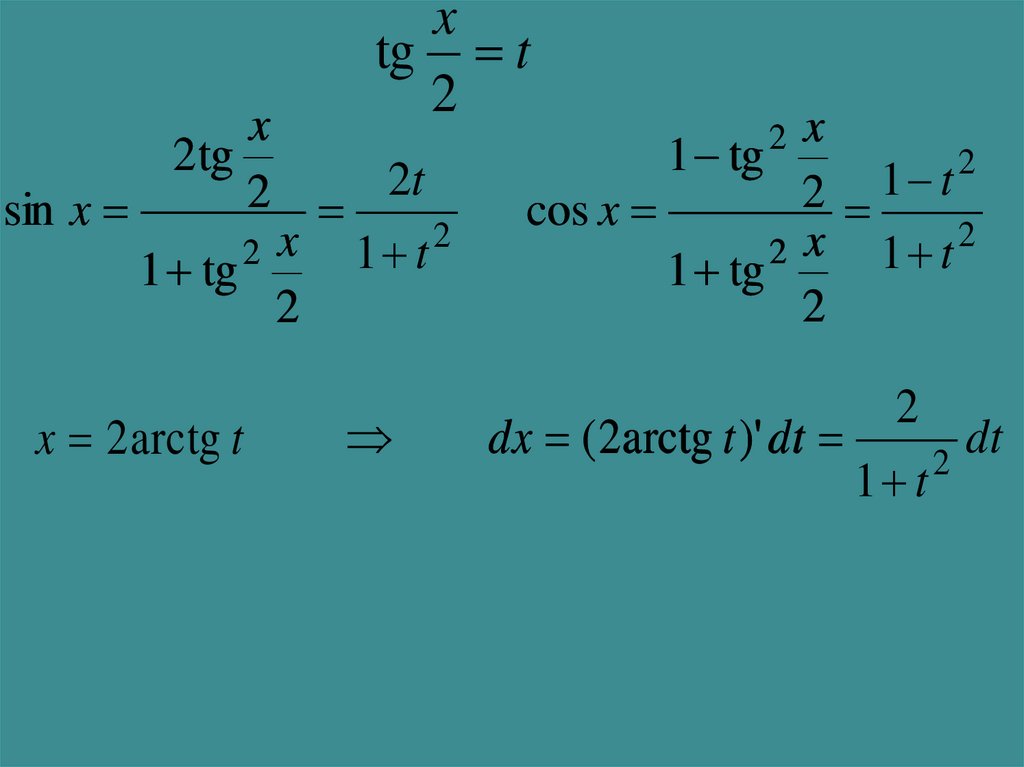


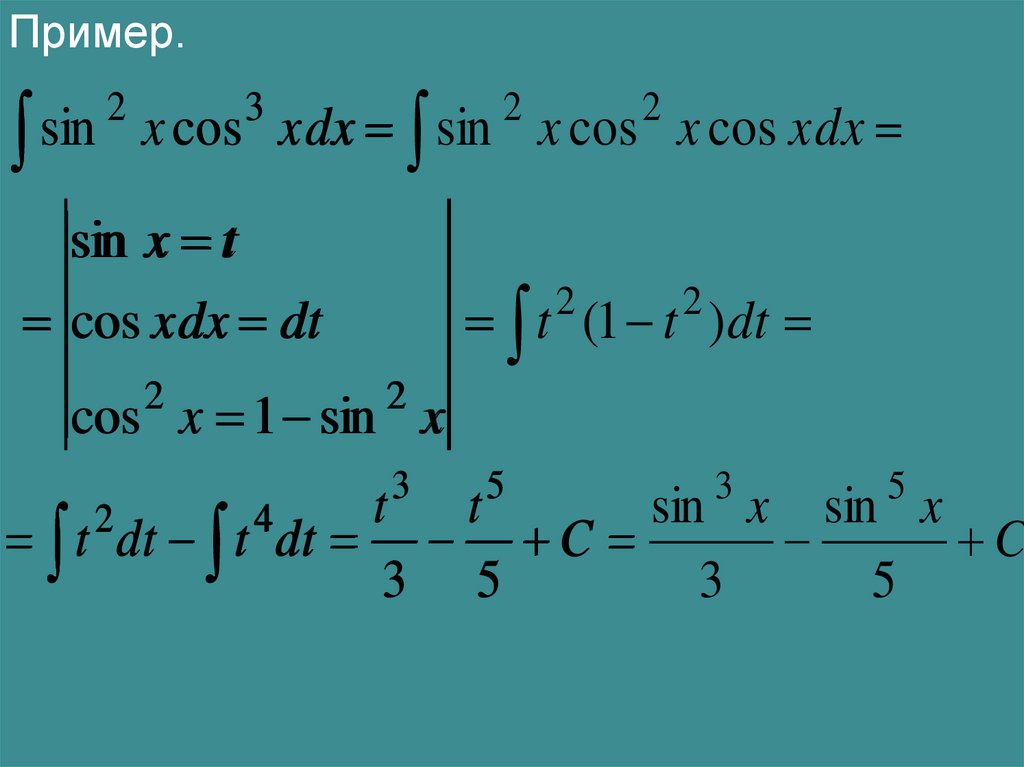
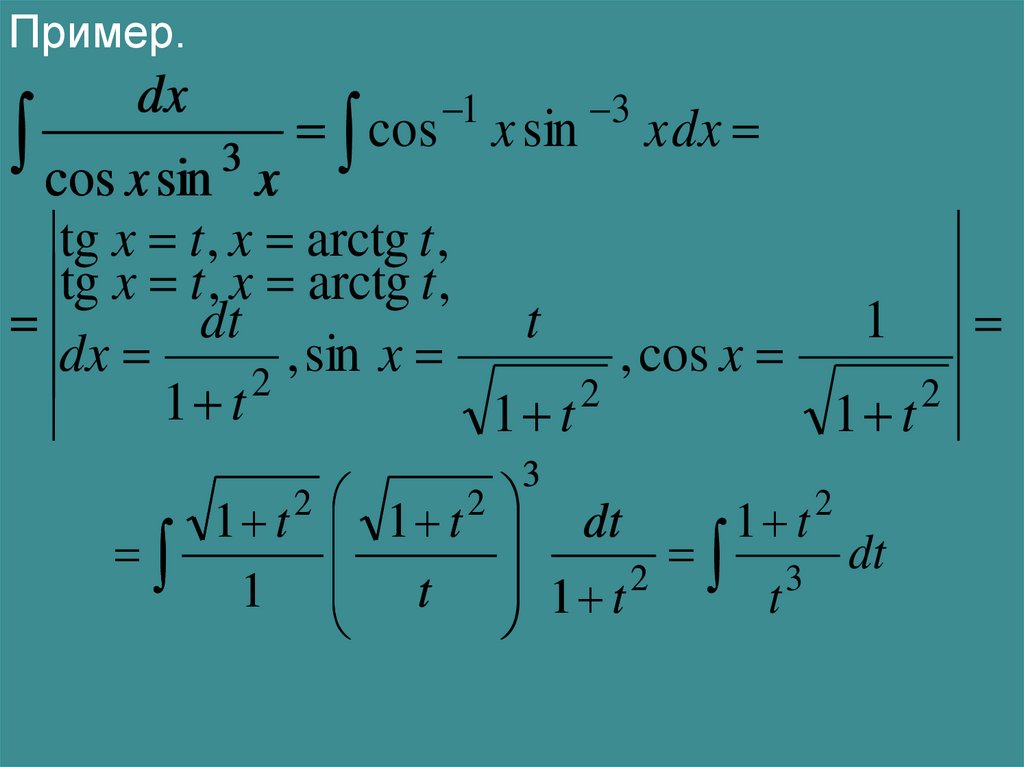
 Математика
Математика








