Производная сложной функции

1.

Тема урока:
Производная
сложной функции

2.

Вставить
пропущенные слова:
1)Производной функции в точке x0
называется число, к которому стремится
функции к приращению аргумента
отношение приращения
__________________________________
f
, при x 0.
x
2) Нахождение производной функции f
дифференцированием
называется ____________________.
сумме производных
3) Производная суммы равна ________________.
4) Постоянный множитель можно выносить за
знак производной
________________.

3.

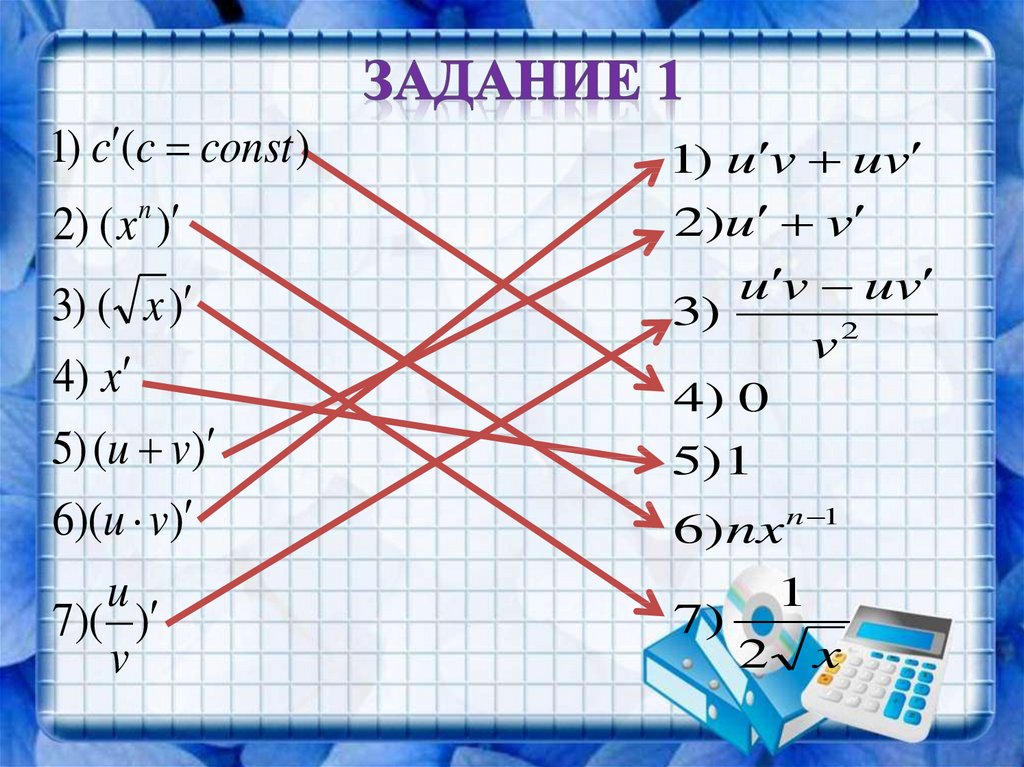
1) c (c const )
2) ( x )
n
3) ( x )
4) x
5) (u v)
6)(u v)
u
7)( )
v
1) u v uv
2)u v
u v uv
3)
v2
4) 0
5)1
6) nx n 1
1
7)
2 x

4.

Задание 2.
Найдите производные
функций
.

5. Группа 1

1) f ( x) 3x x x 7 1) f ( x) 12 x 3 2 x 1
4
2
2) f ( x) 5x 2 x 8x 2) f ( x) 30 x 6 x 8
6
3) f ( x) x 2 x
3
4) f ( x) x x 4 x
4
5
3
5) f ( x) (2 x 3)
5
3) f ( x)
1
2
2
2 x
3
4
4) f ( x) 4 x 3x 4
5) f ( x) ?

6. Группа 2

1
1) f ( x) 3 x
x
1
3
2) f ( x) x 8 x 11
1
3) f ( x) x 6 x
x
2
4
4) f ( x) x 2 x
5
5) f ( x) 3x 7
1) f ( x ) 3 x 4 1
2
3
1
2) f ( x ) x 8
3
1
1
3) f ( x )
2 6
x
2 x
4) f ( x ) 4 x 5 2
5) f ( x ) ?

7. Группа 3

10 x 3
1) f ( x)
3x 1
x 1
2) f ( x)
5x 4
4x 1
3) f ( x )
x 2
5x 6
4) f ( x )
2x 3
1
5) f ( x)
(7 x 3) 5
1
(3 x 1) 2
9
2) f ( x)
(5 x 4) 2
9
3) f ( x)
( x 2) 2
3
4) f ( x)
( 2 x 3) 2
5) f ( x) ?
1) f ( x)

8.

• Сложная функция – функция от
функции.
• h(x)=f(g(x))
• f(x)- внешняя функция
• g(x)-внутренняя функция
• Примеры:
h( x) (5x 4)
3
1
h( x )
2x 4
h( x ) 4 x 3

9. Алгоритм вычисления производной сложной функции h(x) = f(g(x)).

1) Определить внутреннюю функцию g(x).
2) Найти производную внутренней функции g'(x)
3) Определить внешнюю функцию f(g)
4) Найти производную внешней функции f'(g)
5) найти произведение производной внешней
на производную внутренней функции
h’(x) = f’(g(x))·g’(x)

10. Задание 3.

• Задайте формулами элементарные функции f и
g, из которых составлена сложная функция
h(x)=f(g(x))
1) h( x) (3 5 x)
5
2) h( x) (2 x 1)
7
1) f ( x) x 5 , g ( x) 3 5 x.
2) f ( x ) x 7 , g ( x ) 2 x 1.
3)h( x) x 4 x
3) f ( x) x , g ( x) x 4 x.
1
4) h ( x ) 3
x 2
4
5)h( x) (7 x)
1
3
4) f ( x ) , g ( x ) x 2.
x
4
5) f ( x) x , g ( x) 7 x.
2
2

11. Задание 4. Определите правильный ответ

1) f ( x) (4 x 8)
6
2) f ( x) x 1
1
3) f ( x)
5
(6 x 1)
2
5
1) f ( x ) 24( 4 x 8)
1
3) f ( x)
2 x2 1
30
5) f ( x )
4
(6 x 1)

12.

13.

14.

15.

Задание 6. Тесты
А
7
1 f ( x) 63( x 9)
f ( x) ( x 9)
f ( x) ( x 4)
2
3
f ( x) 8 3x
f ( x) x 4
1
f ( x)
( x 3)5
1
f ( x)
(3x 5) 4
1 3
f ( x) (2 x )
4
2
3
4
5
О
6
С
f ( x) 7( x 9) 6 f ( x) 7( x 9)8
Т
К
Т
А
Б1
Л3
f ( x) 6x( x 2 4) 2 f ( x) 6x( x 2 4) 4 f ( x) 6( x 2 4) 2
3
8 3x
f ( x)
П
f ( x)
f ( x)
1
x 4
Ч 5
( x 3) 6
Е 12
f ( x)
f ( x)
2 8 3x
И1
2 x 4
Е
5
f ( x)
( x 3) 6
Н
f ( x)
2 8 3x
f ( x)
f ( x)
Т4
x 4
О
5
( x 3) 4
Т3
6
f ( x)
7
У 1
О
3К 1 2
f ( x) (2 x ) f ( x) 3(2 x ) 4 f ( x) 6(2 x 1 ) 2
4
4
4
4
(3x 5) 5
12
f ( x)
(3x 5) 5
f ( x)
(3x 5) 5

16.

Дополнительные задания
1) f ( x) ( x 5x 7)
3
2
2) f ( x) (8x 3x)
2
3) f ( x)
4) f ( x)
3
4
1
x 5
1
2x 4
4
5

17.

1) f ( x ) 4 x 3 2 x 2 3
1
2) f ( x ) 7 x 4 x
2
3) f ( x ) 5 x
x
4) f ( x ) x 3
5) f ( x ) x 5 9 x 4 8 x
1
6) f ( x ) x 3 2
x
7) f ( x ) x 55
8) f ( x ) 0,5 x 4 0,75

18.

1) f ( x ) 2 x 2 3 x
2) f ( x )
4
x 11
1
3) f ( x ) x 3
x
2
1
4) f ( x ) x x
4
5) f ( x ) x 7 9 x 2 4 x
6) f ( x ) x 4
7) f ( x ) 3 x 2 2 x 2 x 5
8) f ( x ) 0,5 x 2 0,25

19.

5
x 70
2) f ( x ) 5 x
1) f ( x )
3) f ( x ) x x
x
12
4) f ( x )
9
1 2
x 8x
5) f ( x )
2
6) f ( x )
4
x3
7) f ( x ) 36 x
8) f ( x ) 0,5 x 4 0,5