Расчет электрических цепей постоянного тока, не содержащих источников ЭДС

1.

Расчет электрических цепей
постоянного тока, не содержащих
источников ЭДС

2.

1.Последовательное соединение резисторов
Резистор – элемент цепи с заметным сопротивлением
R
I
R1
U1
R2
R3
U2
U3
U
I
Rобщ
I const
U U1 U 2 U 3 ...
IR IR1 IR2 IR3 ...
Rобщ R1 R2 R3 ...
U

3.

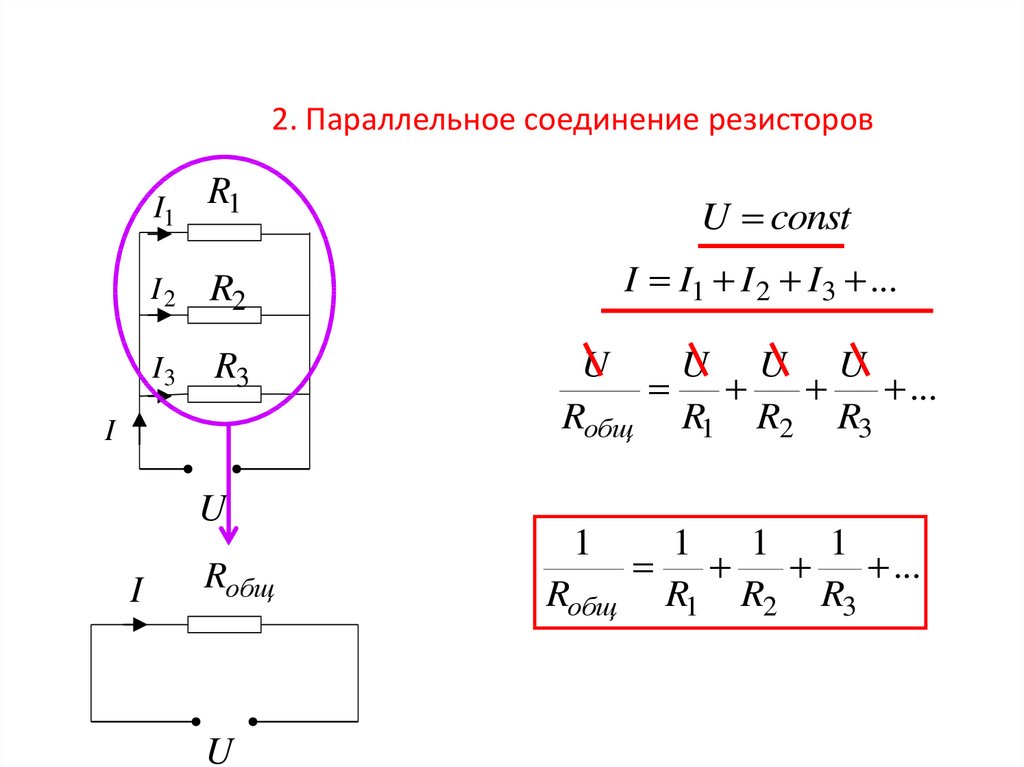
2. Параллельное соединение резисторов
I1
R1
I2
R2
I3
R3
I
U const
I I1 I 2 I 3 ...
U
U U U
...
Rобщ R1 R2 R3
U
I
Rобщ
U
1
Rобщ
1
1
1
...
R1 R2 R3

4.

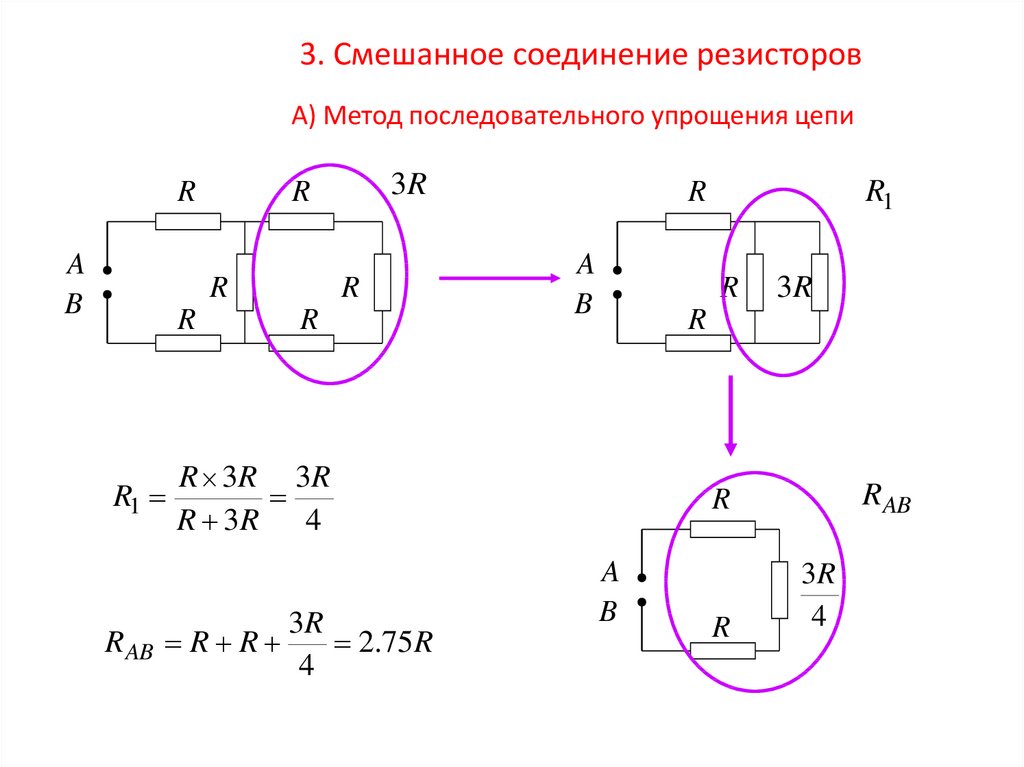
3. Смешанное соединение резисторов
А) Метод последовательного упрощения цепи
R
A
B
R
R
R1
3R
R
R
R
A
B
R
3R
2.75R
4
3R
R
R 3R 3R
R 3R
4
R AB R R
R1
R
RAB
R
A
B
R
3R
4

5.

Б) Метод поиска точек с одинаковыми потенциалами
Если две точки цепи имеют одинаковые потенциалы, то
1) Их можно соединять
2) Их можно разъединять
3) Резисторы, включенные между ними, можно исключить
Как узнать, что потенциалы точек одинаковы?
Точки имеют одинаковые потенциалы, если:
1) Они соединены проводником с нулевым сопротивлением
2) Они симметричны геометрически и по отношению к
точкам подключения

6.

Задача
Определить сопротивление проволочного куба при подключении к двум
наиболее удаленным друг от друга вершинам. Сопротивление каждого ребра
куба равно R
B
F
C
A B
C D E
F G H
G
D
A
H
E
A
C
D
R E
3
R
6
F
G
H R
3
B

7.

В) Общий метод расчета общего сопротивления
R2
R1 C
A
B
R5
R3
RAB - ?
R4
R1 R3
R2 R4
C D
R1 R3
R2 R4
C D
D
I
I
U
Приложим к концам цепи напряжение U
и рассчитаем ток I, протекающий через
цепь
По закону Ома
R
U
I

8.

I1
A
R1 C
I5
I2
Найти: I, I1, I2, I3, I4, I5
B
R5
R3
I3
R2
Дано: U, R1, R2, R3, R4, R5
Необходима система из 6 неза-висимых
уравнений для токов
R4
D
I4
I
I
U
Закон сохранения заряда:
A : I I1 I 3
(1)
B : I I2 I4
C : I1 I 2 I 5
D : I3 I5 I 4
(2)
(3)

9.

I1
A
R1 C R2 I 2
R5
R4
R3
I 3 D I 4
I5
Работа сил электрического поля над
зарядом не зависит от траектории
движения заряда
B
I
I
U
Работа сил электрического поля над
зарядом при премещении по замкнутому
контуру равна нулю
ADCB : I 3 R3 I 5 R5 I 2 R2 U (4)
ACBDA : I1R1 I 2 R2 I 4 R4 I3R3 0 (5)

10.

Записанные уравнения объединим в систему:
I I1 I3 0
I I2 I4 0
I1 I 2 I5 0
I1R1 I5 R5 I 2 R2 U
I1R1 I 2 R2 I 4 R4 I3R3 0
Общее решение системы имеет вид
I U f ( R1, R2 , R3 , R4 , R5 )
По определению
R
U
I
1
f ( R1, R2 , R3 , R4 , R5 )

11.

Расчет разветвлённых электрических
цепей постоянного тока, содержащих
источники ЭДС

12.

1. Метод Кирхгофа
Сложная электрическая цепь постоянного тока содержит произвольным
образом соединенные источники тока и резисторы.
Задача расчета сложной цепи состоит в определении всех неизвестных
токов, текущих в цепи.
В методе Кирхгофа расчёт начинается с расстановки токов, текущих в
ветвях схемы. Направление тока в каждой ветви выбирается произвольно.
2
1
R1
A
I2
I4
I1
R2
3
R4
R3
I3
R5
I5
4
B
C

13.

Общее число уравнений, составленных для расчёта цепи, равно числу
неизвестных токов.
2
1
R1
A
I2
I4
I1
R2
3
R4
R3
I3
R5
I5
C
4
B
В данной цепи для расчета токов I1, I2, I3, I4, I5 необходимо составить 5
независимых уравнений
Для составления уравнений используются 2 правила Кирхгофа

14.

2
1
R1
A
I2
I4
I1
R2
3
R4
R3
I3
R5
I5
C
4
B
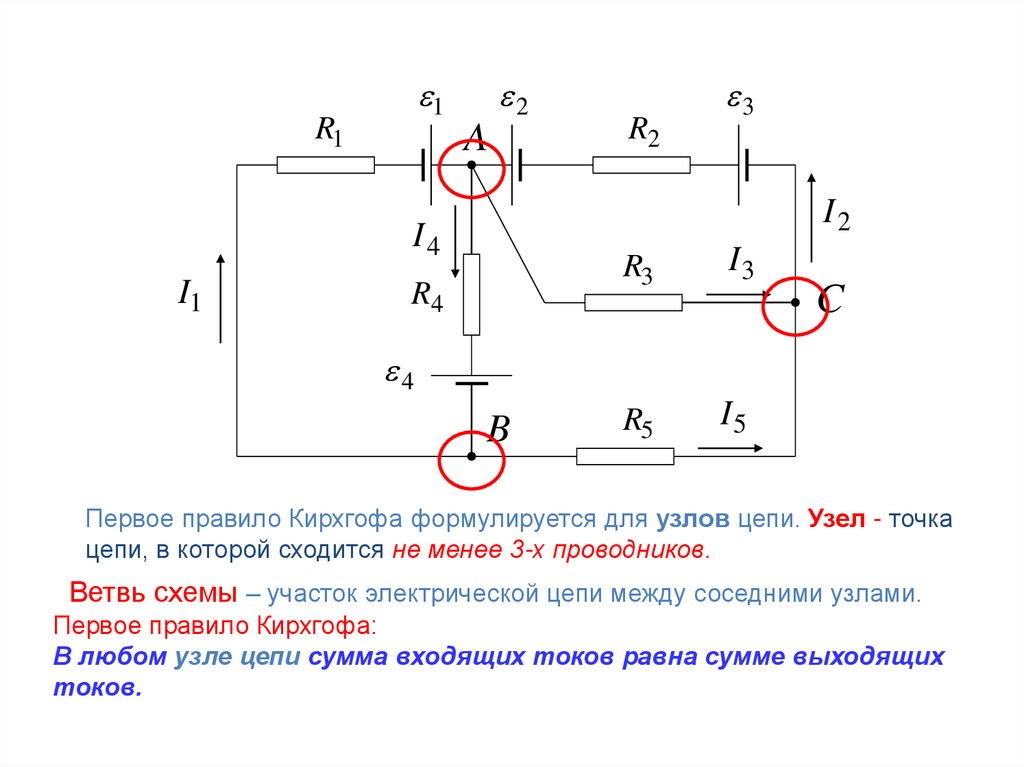
Первое правило Кирхгофа формулируется для узлов цепи. Узел - точка
цепи, в которой сходится не менее 3-х проводников.
Ветвь схемы – участок электрической цепи между соседними узлами.
Первое правило Кирхгофа:
В любом узле цепи сумма входящих токов равна сумме выходящих
токов.

15.

2
1
R1
R2
A
I2
I4
I1
3
R4
R3
I3
R5
I5
C
4
B
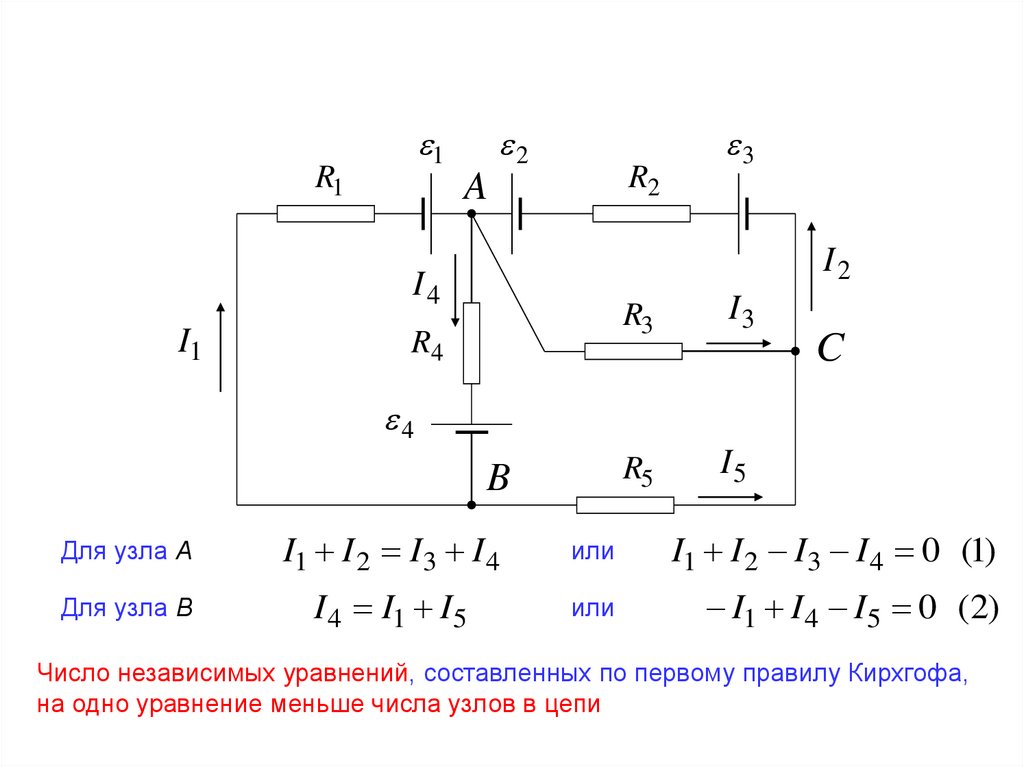
Для узла А
I1 I 2 I3 I 4
или
I1 I 2 I3 I 4 0 (1)
Для узла В
I 4 I1 I5
или
I1 I 4 I5 0 (2)
Число независимых уравнений, составленных по первому правилу Кирхгофа,
на одно уравнение меньше числа узлов в цепи

16.

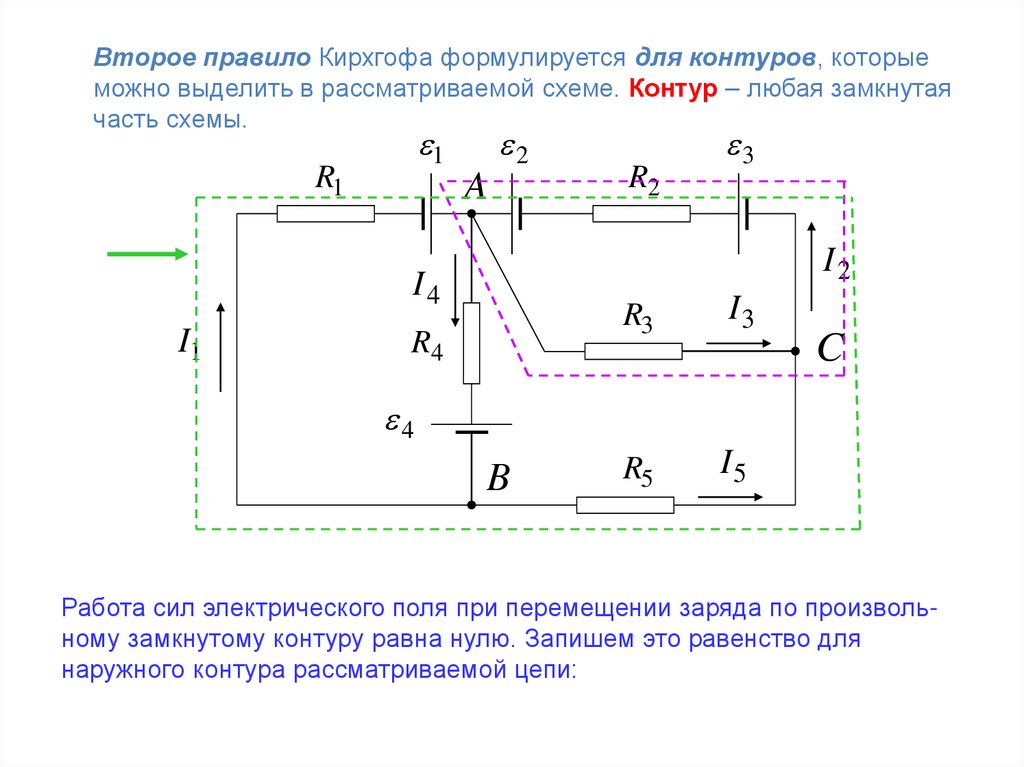
Второе правило Кирхгофа формулируется для контуров, которые
можно выделить в рассматриваемой схеме. Контур – любая замкнутая
часть схемы.
2
1
3
R1
R2
A
I2
I4
I1
R4
R3
I3
R5
I5
C
4
B
Работа сил электрического поля при перемещении заряда по произвольному замкнутому контуру равна нулю. Запишем это равенство для
наружного контура рассматриваемой цепи:

17.

R1
1
2
3
R2
I1
q
R5
I5
ЭП
ЭП
ЭП
ЭП
ЭП
ARЭП
A
A
A
A
A
1
2
R2
3
R5 0
1
qI1R1 q 1 q 2 qI 2 R2 q 3 qI 5 R5 0
I1R1 I 2 R2 I5 R5 1 2 3
I2

18.

Второе правило Кирхгофа:
Для любого замкнутого контура цепи, при выбранном направлении обхода
контура, алгебраическая сумма напряжений на резисторах контура равна
алгебраической сумме ЭДС источников тока, встреченных при обходе
контура. Направление обхода контура выбирается произвольно.
В сумму напряжений на резисторах слагаемые входят со знаком «+», если
направление тока текущего через резистор, совпадает с направлением
обхода, и со знаком «-», если направления противоположны.
В сумму ЭДС слагаемые входят со знаком «+», если направление ЭДС,
Источника совпадает с направлением обхода, и со знаком «-», если
направления противоположны
Число независимых
уравнений, которые можно
составить по второму правилу
Кирхгофа равно числу
простых контуров цепи
1
R1
1
R4
2
3
R2
R3
4
R5
2
3

19.

2
1
R1
A
I2
I4
I1
R2
3
R4
R3
I3
R5
I5
C
4
B
BR1R2CB :
I1R1 I 2 R2 I5 R5 1 2 3
(3)
BAR2CB :
I 4 R4 I 2 R2 I5 R5 4 2 3
(4)
AR3CR2 A :
I3R3 I 2 R2 3 2
(5)

20.

I1 I 2 I3 I 4 0
(1)
I1 I 4 I5 0
(2)
I1R1 I 2 R2 I5 R5 1 2 3
(3)
I 4 R4 I 2 R2 I5 R5 4 2 3 (4)
I3R3 I 2 R2 3 2
(5)
Для любой сколь угодно сложной цепи правила Кирхгофа позволяют
составить достаточное число независимых уравнений для нахождения всех
токов в цепи

21.

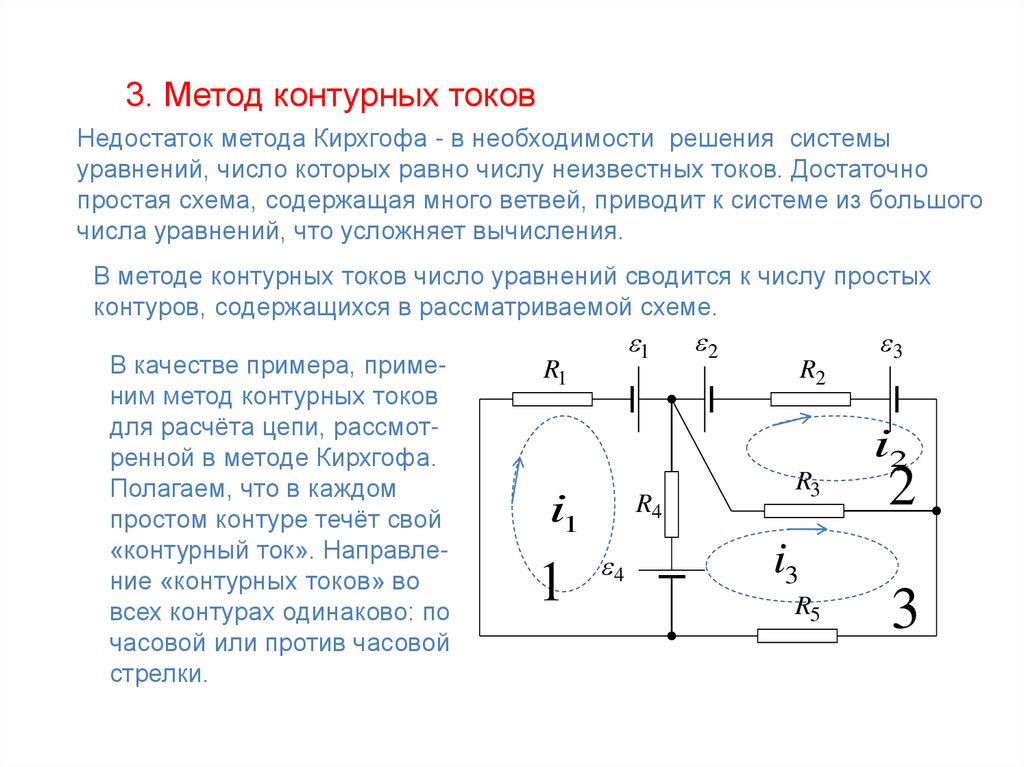
3. Метод контурных токов
Недостаток метода Кирхгофа - в необходимости решения системы
уравнений, число которых равно числу неизвестных токов. Достаточно
простая схема, содержащая много ветвей, приводит к системе из большого
числа уравнений, что усложняет вычисления.
В методе контурных токов число уравнений сводится к числу простых
контуров, содержащихся в рассматриваемой схеме.
В качестве примера, применим метод контурных токов
для расчёта цепи, рассмотренной в методе Кирхгофа.
Полагаем, что в каждом
простом контуре течёт свой
«контурный ток». Направление «контурных токов» во
всех контурах одинаково: по
часовой или против часовой
стрелки.
1
R1
i1
1
R4
4
2
R2
R3
i3
R5
3
i2
2
3

22.

Для нахождения «контурных токов», для каждого контура составляется
уравнение по второму правилу Кирхгофа.
Для конура №1:
Для контура №2
Для контура №3
R1i1 (i1 i3 ) R4 1 4
(1)
R2i2 (i2 i3 ) R3 2 3
(2)
R5i3 R4 (i3 i1 ) R3 (i3 i2 ) 4
(3)
Раскрывая скобки и приводя подобные получим систему уравнений для
нахождения «контурных токов»:
R1 R4 i1 R4i3 1 4
R2 R3 i2 R3i3 2 3
R4i1 R3i2 R3 R4 R5 i3 4
После решения системы возвращаемся к исходной схеме, и находим
неизвестные токи, текущие в ветвях схемы:

23.

I1 i1; I 2 i2 ; I 3 i3 i2 ;
I 4 i3 i1;
I 5 i3
Полученное с отрицательным знаком значение тока свидетельствует о
противоположном предполагаемому направлении тока в данной ветви.
Сокращение числа уравнений на два, по сравнению с методом Кирхгофа,
делает применение метода контурных токов более предпочтительным.