Мощности начала и конца линии электропередач (ЛЭП)

1. МОЩНОСТИ НАЧАЛА И КОНЦА ЛЭП

2.

При анализе режимов работы длинных линий часто
бывает необходимо выявить соотношения между
мощностями в начале и конце ЛЭП.
Для анализа будем считать линию идеальной.
U1 U 2 cos Л j 3 Z C I 2 sin Л ;
U2
I
I
cos
j
sin Л ;
2
Л
1
3 ZC
Выразим ток в начале передачи через напряжения по
её концам:
U U 2 cos Л
I2 1
;
j 3 Z C sin Л
U1 cos Л U 2 cos 2 Л U 2 U1 cos Л
U2
I1 j
sin Л
.
3 ZC
j 3 Z C sin Л
3 Z C sin Л

3.

Мощность в начале линии:
*
*
U 2 U1 cos Л
S1 3 U1 I 1 P1 jQ1 3 U1 j
3 ZC sin Л
*
2
U cos Л
U 2 U1
j
j 1
;
ZC sin Л
ZC sin Л
U12 cos Л
j U 2 U1 cos j U 2 U1 sin
S1
j
;
ZC sin Л
ZC sin Л
где - угол между векторами напряжения в начале и конце
линии;
U 2 cos
U U cos
U 1 U 2 sin
U
U
cos
2
Л
1
Л
S1
j 1
1 2
ZC sin Л
ZC sin Л
ZC sin Л j 3 ZC sin Л
j
U 2 U1 cos Л
.
3 ZC sin Л

4.

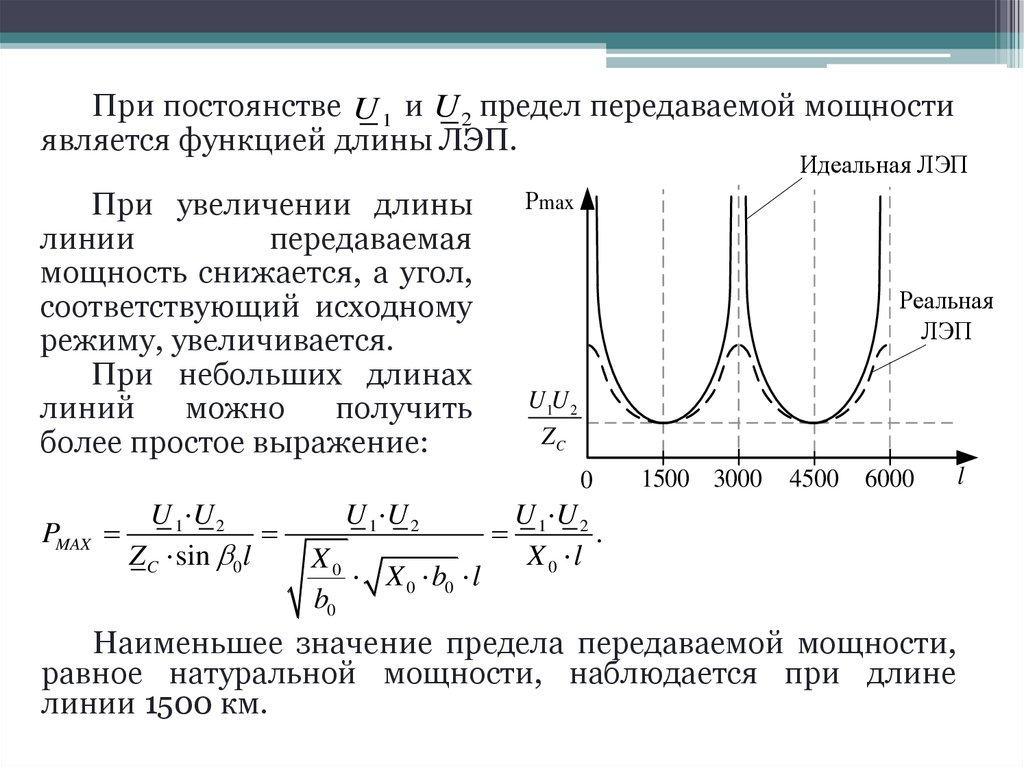
При постоянстве U 1 и U 2 предел передаваемой мощности
является функцией длины ЛЭП.
Идеальная ЛЭП
При увеличении длины
линии
передаваемая
мощность снижается, а угол,
соответствующий исходному
режиму, увеличивается.
При небольших длинах
линий
можно
получить
более простое выражение:
Рmax
Реальная
ЛЭП
U1U 2
ZC
0
PMAX
U 1 U 2
Z C sin 0l
U 1 U 2
X0
X 0 b0 l
b0
1500 3000
4500
6000
U 1 U 2
.
X0 l
Наименьшее значение предела передаваемой мощности,
равное натуральной мощности, наблюдается при длине
линии 1500 км.
l

5.

Часто, для анализа соотношений между мощностями по
концам ЛЭП, бывает удобно использовать уравнения
четырёхполюсника для линейных значений напряжений.
U 1 A U 2 3 B I 2
C U 2
I1
D I2
3
*
*
S2 3 U 2 I 2 I 2
*
S2
.
3 U 2
Совмещаем вектор U2 c действительной осью.
B S2
U 1 A U 2
U 2
*
C U 2 D S 2
I1
3
3 U 2
*

6.

*
*
B ( P2 jQ2 ) C U 2 D ( P2 jQ2 )
S1 3 U1 I 1 3 A U 2
U2
3 U 2
3
*
*
2
2
B
D
(
P
Q
2
2)
A C U 22 A D ( P2 jQ2 ) B C ( P2 jQ2 )
2
U2
*
*
*
*
*
*
B D ( P22 Q22 )
A C U P2 ( A D B C )
jQ2 ( A D B C ).
2
U2
*
2
2
*
*
Рассуждая аналогично можно получить выражение
для мощности конца электропередачи:
*
2
2
*
*
*
*
B
A
(
P
Q
2
1
1 )
S2 D C U1
P1 ( A D B C ) jQ1 ( A D B C ).
2
U1
*

7.

Потери активной мощности в линии составят:
*
*
2
2
B
D
(
P
Q
2
2
2)
Р Р1 Р2 Re S1 P2 Re A C U 2
2
U2
P2 ( A D B C ) jQ2 ( A D B C ) P2
*
*
*
*
*
*
2
2
*
*
*
*
B
D
(
P
Q
)
2
2
Re ACU 22
P2 ( A D B C 1) jQ2 ( A D B C ) .
2
U2

8.

* 2
Re A C U 2
- потери холостого хода (не зависят от
параметров режима);
* 2
*
*
B
D
P
2
Re
P
(
A
D
B
C
1)
2
U 22
* 2
*
*
B D Q2
Re
jQ
(
A
D
B
C
)
2
U 22
- потери, зависящие от
передаваемой
активной
мощности;
- потери, зависящие от
передаваемой реактивной
мощности;
Максимальный КПД ЛЭП может быть найден из решения
двух уравнений:
d P
0;
dP
d P
0.
dQ